广义指数分布在步加试验中的参数估计

张　莉（西华师范大学数学与信息学院，四川南充637000）

广义指数分布在步加试验中的参数估计

张莉
（西华师范大学数学与信息学院，四川南充637000）

加速寿命试验中的步加试验，可有效地提高产品质量，且操作简单.基于Nelson模型，讨论广义指数分布在步加试验中的参数估计问题，利用EM算法给出了参数估计的显性表达式，通过数据模拟说明了估计方法的有效性和可行性.

广义指数分布；分组数据；步加试验；Nelson模型

Zhang L.Parameter Estimation ofGeneralized ExponentialDistribution in the Step-Stress Accelerated Life Tests[J].JournalofYibin University,2015,15（6）：108-112.

加速寿命试验，是指将受试产品置于非正常应力条件下，通过观察产品的失效情况，从而推断正常应力条件下产品的统计规律性的一种试验.加速寿命试验包括了恒加试验、步加试验、序加试验等，而本文讨论的重点就是步加试验（即将样品置于高于正常应力条件下做的试验），考虑的产品寿命分布为广义指数分布.广义指数分布是1999年由Gupta和Kundu[1]提出的，被后人广泛应用于物理学、经济学等领域.人们对广义指数分布做了许多研究，主要讨论常规寿命试验数据的统计分析方法，研究重点是参数的点估计，如：文献[2]利用EM算法给出了广义指数分布在分组和右截尾数据下的参数估计；文献[3]讨论了广义指数分布的极大似然估计，并得到其渐进分布；文献[4]利用逆矩法估计广义指数分布的未知参数，并给出了构造尺度参数区间估计的方法；文献[5]讨论了广义指数分布在恒加试验中的参数估计.但目前在不完全样本条件下，讨论步加试验中广义指数分布统计特性的文章却少见.

广义指数分布的密度函数、分布函数分别是

f（t）=αλ（1-e-λt）α-1e-λt，t≥0F（t）=（1-e-λt）α，t≥0

其中，α＞0称为模型的形状参数，λ＞0称为模型的尺度参数.当形状参数α=1时，模型即为一般的指数分布模型.

1　基本假定

假设 S0为正常应力条件下的应力水平，S1,S2,...,Sk为非正常条件下的应力水平，并满足S0＜S1＜S2＜...＜Sk.现将n个相互独立的元件在t1,0时刻投入到加速应力水平S1下做寿命试验，到t1,m1时刻为止共有R1个失效，同时将应力水平上升到S2，余下的未失效元件在S2下继续做试验，到t2,m2时观测到有R2个失效，并将应力提高到S3,…这样继续做下去，直到在应力水平Sk下的时刻tk,mk，才停止整个试验，此时有Rk个元件失效.记

t0=t1,0=0,tk=tk,mk,ti=ti,m i=ti+1,0,i=1,2,…,k-1

假设在Si下（i=1,…,k）观察时刻为ti,0,ti,1,…,ti,mi

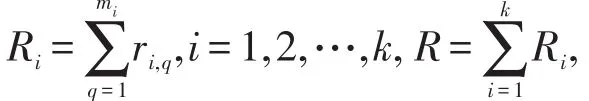
2　参数估计

引理1[6]不同应力水平Si,Sj下产品的失效机理与正常应力水平S0下的失效机理相同，反应在分布参数上即形状参数α不随应力水平变化而变化.

引理2（Nelson模型）[6]产品的参与寿命仅依赖于当时的累积失效部分和当时的应力水平，而与累积方式无关.即在应力水平Si下工作ti时间的累积失效率FSi（ti）相当于该产品在应力水平Sj下工作tj时间的累积失效率FSj（tj），即：FS1（t1）=FSj（tj），i,j=1,2,…,k.

有效力矩型螺纹紧固件(图4)俗称“自锁螺栓和自锁螺母”，它通过在紧固件和配对物间形成螺纹接合面来防止紧固件松动。

定理1根据基本假定，参数的极大似然估计可以由隐性表达式

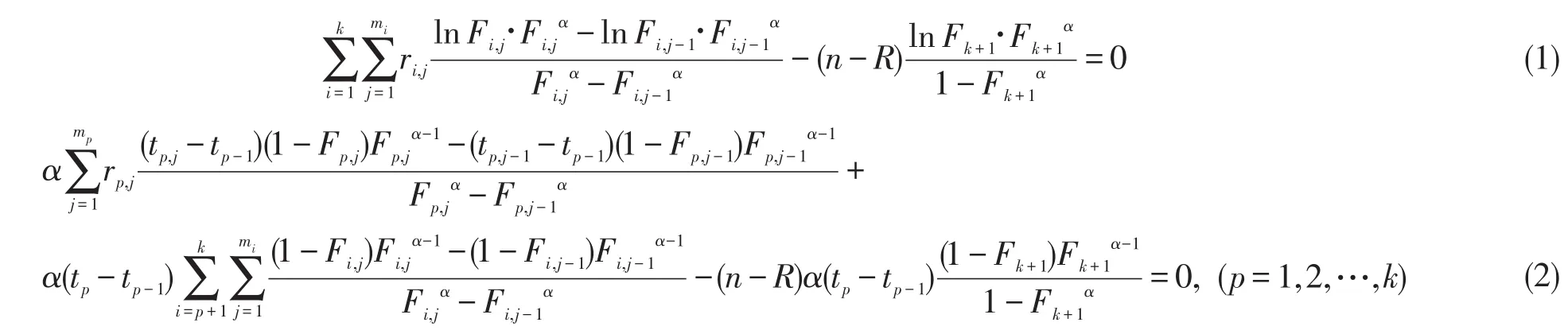
求解.

证明：为求参数估计，先做其对数似然函数

为求各参数的估计值，将对数似然函数关于各参数求偏导并令其等于零，得到表达式（1）、（2）.

（1）、（2）式是含有各参数的隐性表达式，但形式复杂，若要得到各参数的估计值，一般只能用数值迭代获得近似解.为得到参数的显性表达式，且保证精确性，考虑EM算法.

3　EM算法

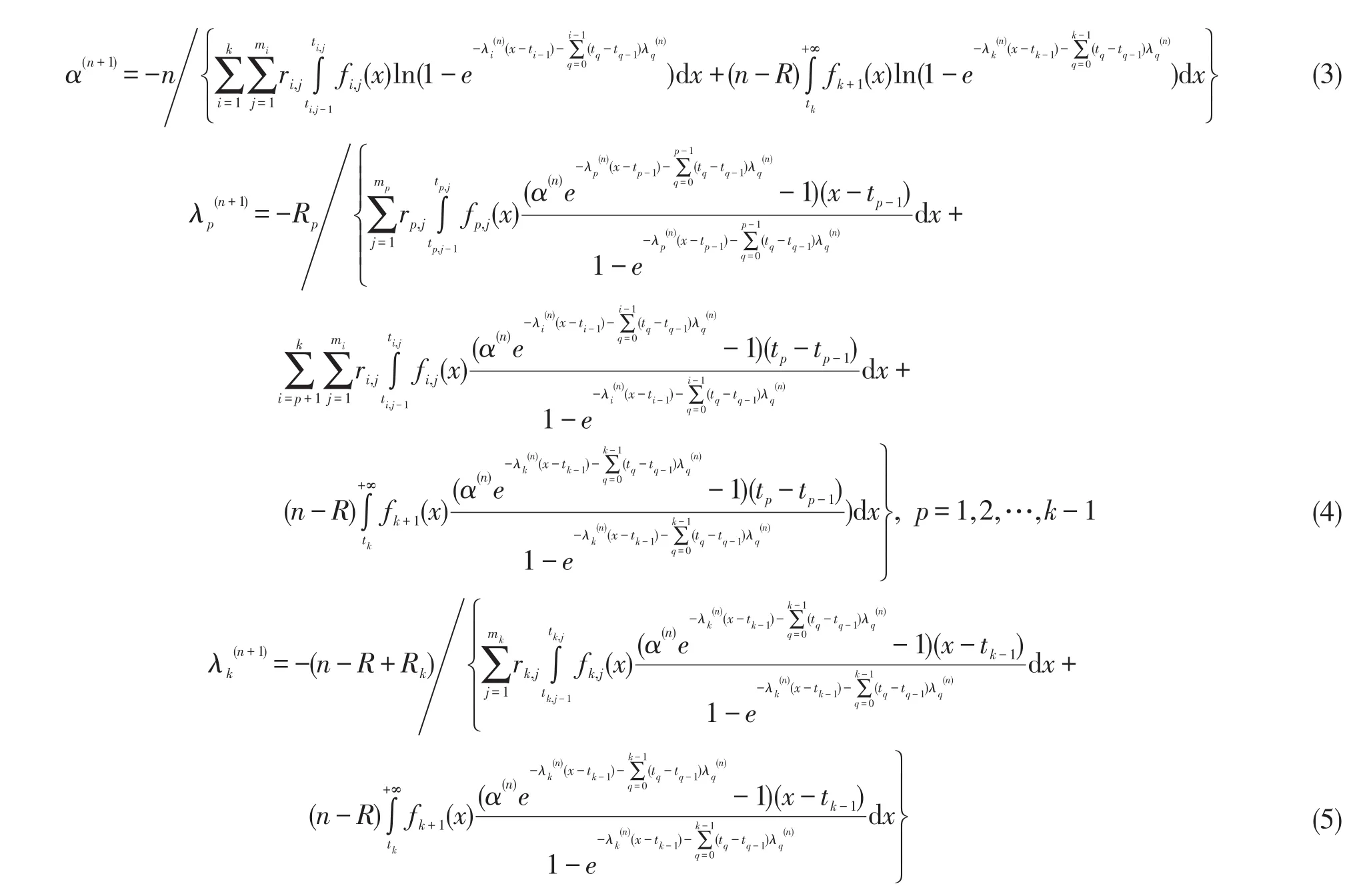
定理2根据基本假定，参数估计值的显性表达式为：

证明：设n个产品的寿命X1,X2,…,Xn独立同分布于广义指数分布，记X=（X1,X2,…,Xn），X是不可观测的，能观测到的是Y=（r1,1,r1,2,…,r1,m1；…；rk,1,rk,2,…,rk,mk；n-R），它们一起构成了完全数据Z=（X,Y）.为了应用EM算法，再引入随机变量Xih，Xw，它们分别表示落入区间（ti,j-1,ti,j]和（tk,+∞）的产品寿命.

下面根据EM算法中的E步和M步来获得参数的极大似然估计.

由于X的信息包含了观测结果Y所有的信息，于是有

p（α,λ|X,Y）=p（α,λ|X）

其中λ=（λ1,λ2,…,λk）.

由广义指数分布的密度函数可以得到

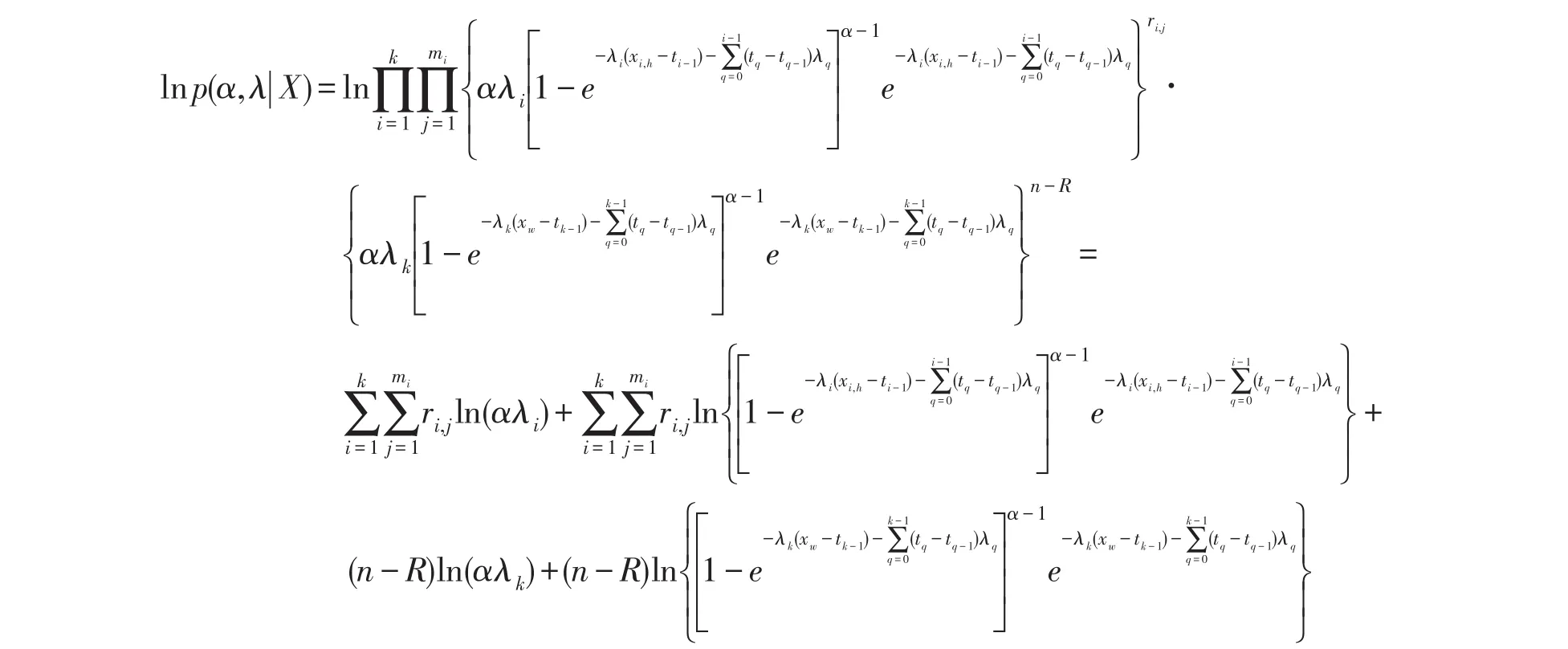
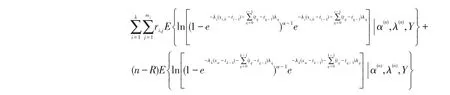
E步：给定参数的第n步估计α（n），λ（n），则第n+1步的Q函数为

当ti,j-1＜X≤ti,j（i=1,2,…,k）时，X的条件密度函数为

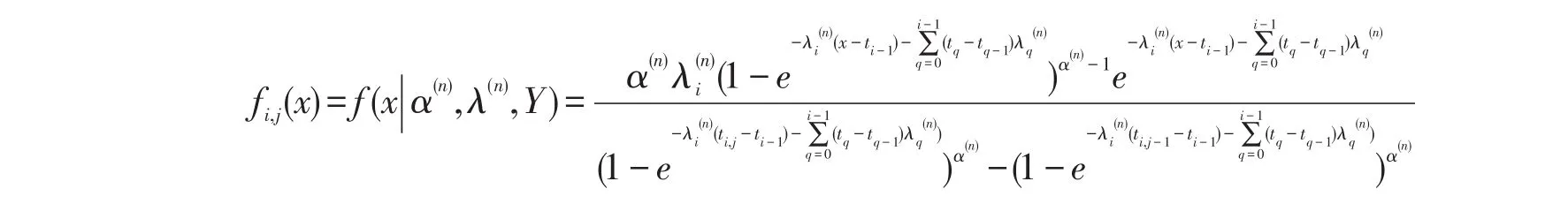
当X＞tk时，X的条件密度函数为

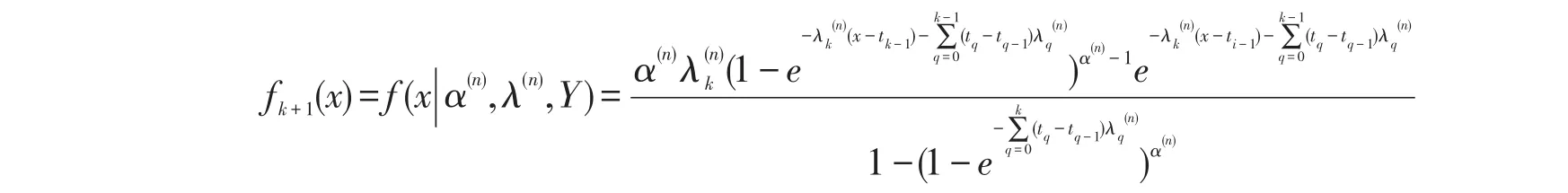
则

M步：极大化Q函数的参数α,λ的第n+1步估计α（n+1），λ（n+1），即将Q（α,λ|α（n）,λ（n）,Y）分别对参数α、λ求导，并令其等于零，得到Q（α,λ|α（n）,λ（n）,Y）的极大值点α（n+1）、λ（n+1）.

经过整理，得到

这样就完成了一次迭代（α（n）,λ（n））→（α（n+1）,λ（n+1）），重复上述步骤直到（α,λ）收敛为止.

4　数据模拟

运用Monte Carlo方法产生在简单步加试验下服从广义指数分布的随机数，其参数真值记作α=2,λ1=0.5,λ2=1.选择样本量为 n=1000的模拟，产生1 000次随机数，观测时刻设为 t1,1=5, t1,2=10,t2,1=15,t2,2=20.通过有限次迭代和数据整理后，得到表1的结果.

表1　随机数的迭代结果

由表1可见，参数估计值与真值非常接近，且相对误差很小，这说明估计的精度较好，方法行之有效.

[1]Gupta RD,Kundu D.Generalized exponengtialdistribution[J].Australian and New Zealand Journalofstatistics,1999,41（2）：173-188.

[2]田玉柱,田茂再,陈平.数据分组和右截尾数据情形下广义指数分布的参数估计及应用[J].数学进展,2012,6（12）：755-762.

[3]沈作斌.广义指数分布下区间删失数据的参数估计[J].教育教学,2010（2）：20.

[4]唐玉娜,施瑞,王炳兴.广义指数分布的统计推断[J].统计与决策,2008（17）：18-19.

[5]张莉.广义指数分布在恒加试验中的参数估计[J].内江师范学院学报,2013（12）：4-7.

[6]唐玉娜.广义指数分布基于加速寿命试验数据的统计分析[D].杭州：浙江工商大学,2008.

（编校：许洁）

Parameter Estimation of Generalized Exponential Distribution in the Step-Stress Accelerated Life Tests

ZHANG Li
（DepartmentofMath and Information,ChinaWestNormalUniversity,Nanchong,Sichuan 637000,China）

The step-stressaccelerated life tests can improve thequality of productsand have the advantagesof simple op⁃eration.The parameter estimation of generalized exponential distribution in the step-stress accelerated life testswas dis⁃cussed based on Nelsonmodel.The two-parameter concrete expressionswere given by using EM algorithm.The estima⁃tionmethodwasproved rightby takingadvantageofMonte Carlo stimulation.

generalized exponentialdistribution；grouped data；the step-stressaccelerated life tests；Nelsonmodel

O213

A

1671-5365（2015）06-00108-05

2014-09-25修回：2014-09-30

西华师范大学科研启动基金（08b025）

张莉（1982－），女，讲师，硕士，研究方向为概率论与数理统计及其应用、产品的可靠性试验

网络出版时间：2014-10-15 13：00网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20141015.1530.005.htm l

引用格式：张莉.广义指数分布在步加试验中的参数估计[J].宜宾学院学报,2015,15（6）：108-112.