推广的Cantor函数的性质

蹇焕燕，付秋菊，张正亮（宜宾学院数学学院，四川宜宾644007）

推广的Cantor函数的性质

蹇焕燕，付秋菊，张正亮
（宜宾学院数学学院，四川宜宾644007）

通过分析推广的Cantor函数的取值特点，讨论这类特殊函数的连续性、可微性、可积性，得出这个特殊函数不可导点构成[0,1]上的类似于Cantor集的集合.

值域；连续性；可积性；可导性；Cantor函数

Jian HY,Fu QJ,Zhang ZL.Propertiesof Extended Cantor Function[J].Journal of Yibin University,2015,15（6）：121-124.

数学分析[1]讨论的是函数的连续性、可微性、可积性等微观与局部性质，这些函数包括初等函数以及一些特殊函数，如隐函数（组）、积分函数、级数函数、极限函数等.对于由微分形式构成的函数方程在文献[2]中已考虑其可解性与解法，其它形式的函数方程散见于一些习题参考书[3].Cantor函数[4-5]是用其某些性质来定义的一类特殊函数，本文主要讨论由如下形式的函数方程确定的函数，它是Cantor函数的推广.设 f（x）是定义在[0,1]上的函数，且满足以下条件：

首先分析了函数的取值特点，并通过该特点证明当b=2,a＞2时，函数 f（x）在[0,1]上的一致连续性，用两种方法计算出该函数在[0,1]上的定积分，并用迫敛的方法证明了 f（x）在[0,1]上的一些特殊点不可导，这些不可导点构成的是一个类似于Can⁃ tor集的集合，Cantor集的构造方法见文献[6].

1　b=2、a＞2的情形

1.1函数取值情况

为了方便，本文采用集合论中类似于Cantor集的构造方法，先对定义域 [0,1]进行分割，记E

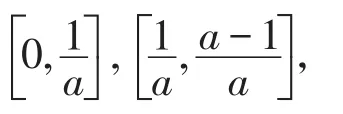
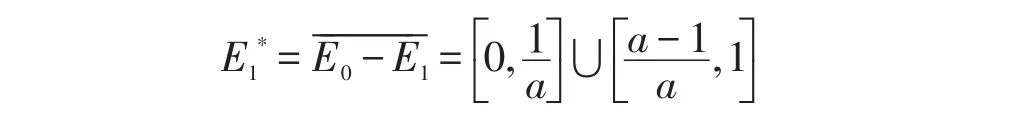
再将E1*的两个区间分别分为3个小区间，即：

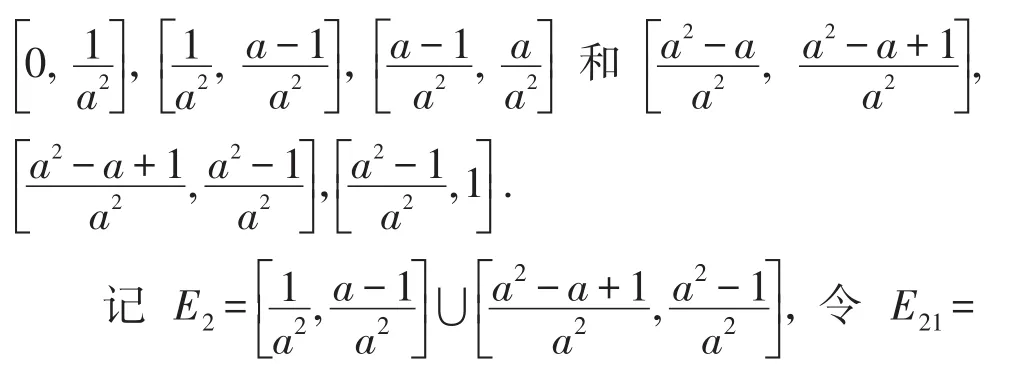
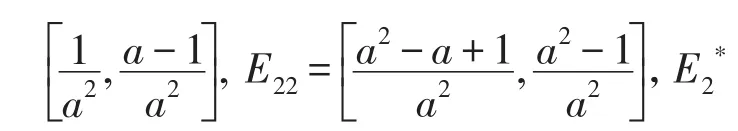
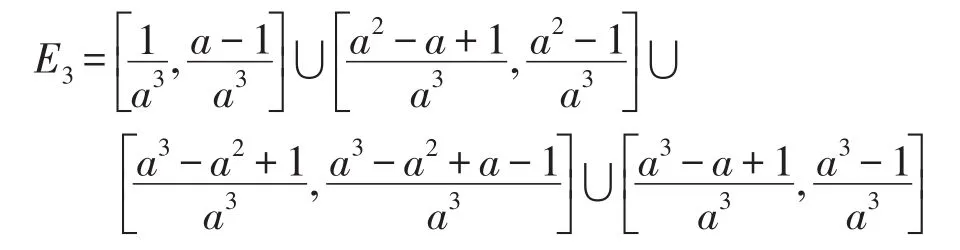
令

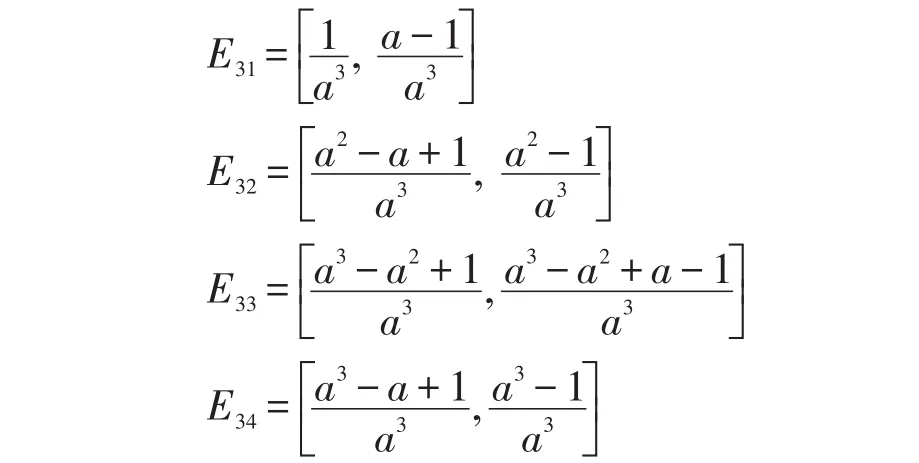
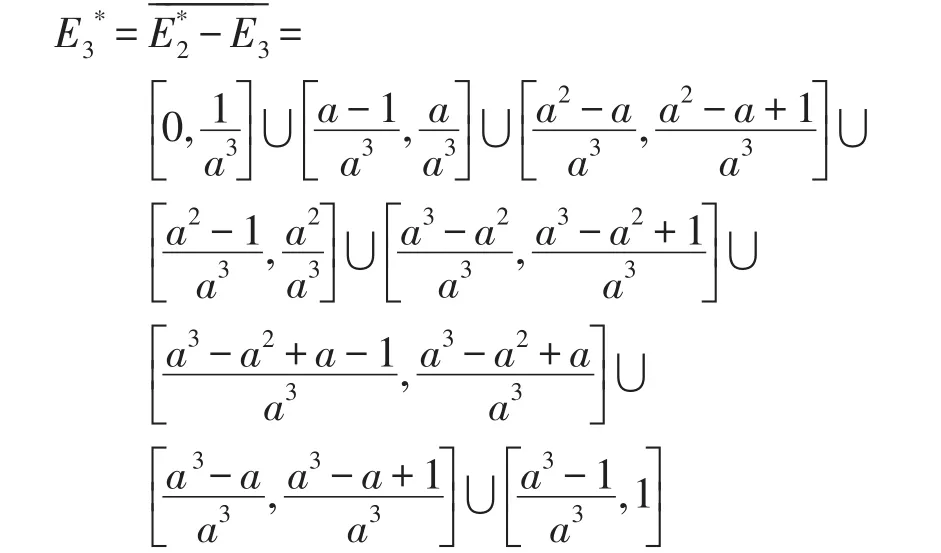
按此方法继续下去，得到一系列小区间Ek、和Eki（k=1,2,…；i=1,2,…2k-1），这些Ek和满足以下特点：

由（1）（2）知 f（0）=0,f（1）=1,在（1）（2）中令可得，再由 f（x）在[0,1]上单增得：

再由（1）得：

又由 f（x）在[0,1]上单增得出：

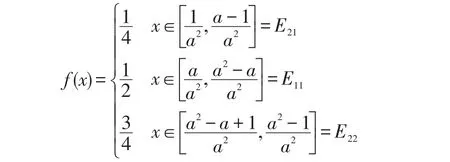
可得：

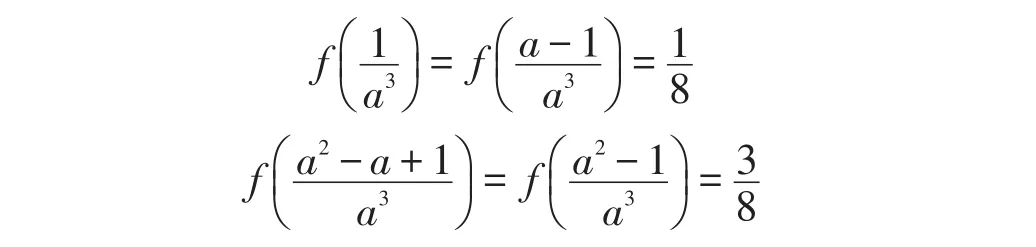
再由（1）得：

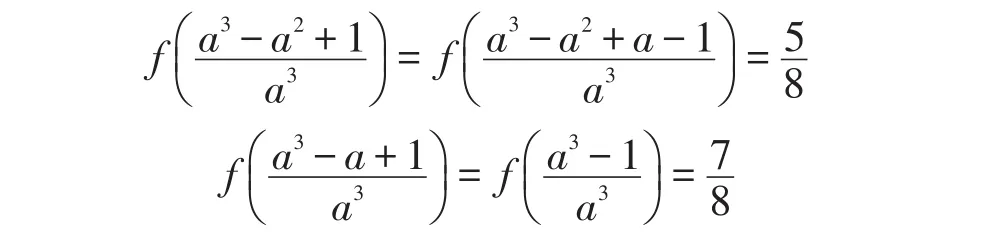
再由 f（x）在[0,1]上单增得：

1.2连续性与一致连续性

定理1f（x）在闭区间[0,1]一致连续，进而连续.

这表明 f（x）在闭区间[0,1]上一致连续，进而f（x）在[0,1]上连续.

1.3可积性

证明：由 f（x）在闭区间[0,1]上连续可得可积性.可积性也可由 f（x）在[0,1]上单增直接得出.

可用以下两种方法求 f（x）在[0,1]上的定积分.

方法一：换元法.

设：

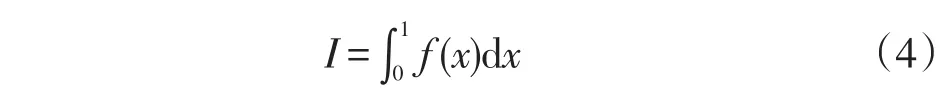
又令x=1-t可得：

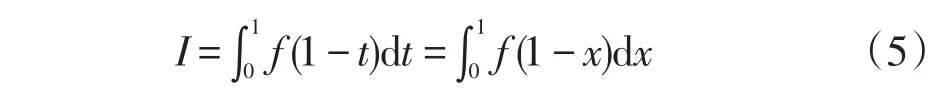
由（4）+（5）得：

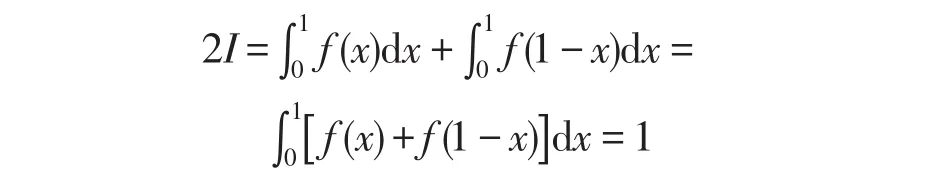
方法二：测度论的方法.

按上述定义域[0,1]的分法，f（x）在[0,1]上的积分就等于E11,E21,E22,E31,E32,E33,E34…等无穷多个区间所对应的小矩形面积之和.

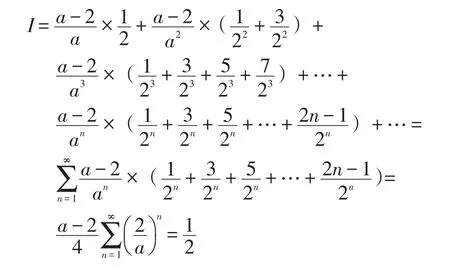
1.4可微性

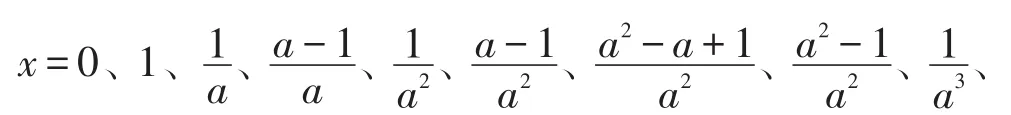
证明：由 f（x）+f（1-x）=1、bf（x）=f（ax）可知，只需证明 f（x）在x=0处右导数不存在，则 f（x）在x=1处左导数不存在，进而在处左导数不存在，从而在处右导数不存在，由此可得：f（x）在…处不可导，而易知在其他点导数是存在的，且为0.

下证 f（x）在x=0处右导数不存在.

因为：

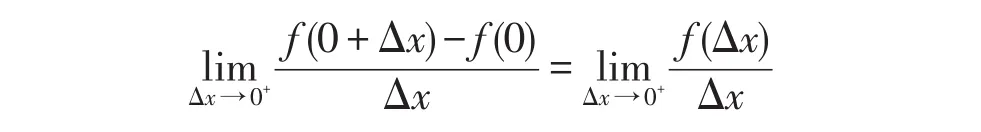
另外：

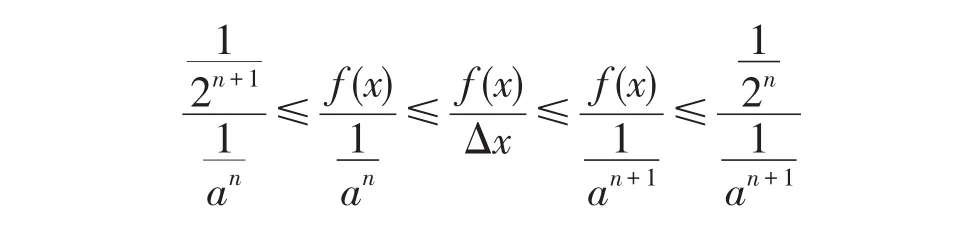
又：

由夹逼定理得：

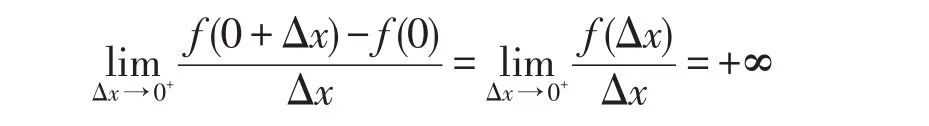
所以 f（x）在x=0处右导数不存在.

说明：当a=3时，不可导点的集合构成Cantor集，从而得出了 f（x）的不可导点构成的集合E具有Cantor集的性质[7]：

性质1：E是完备的非空有界疏朗闭集.

性质2：E是零测集，从而为可测集.

性质3：E的基数为E¯=C.

2　b≠2、a＞b的情形

对于b≠2的情形，由（3）得：f（x）在[0,1]上可积，但它的连续性和可微性又怎么样呢？

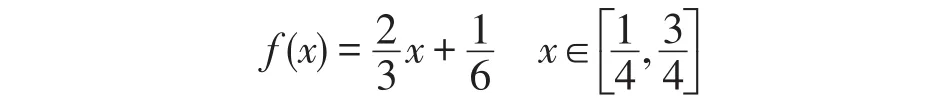
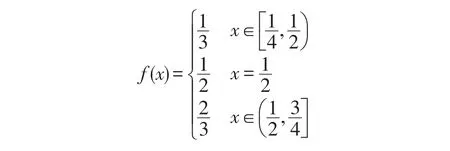
综上，当b≠2,a＞b时，f（x）在[0,1]上的连续性取决于 f（x）在是否连续，所以该函数在[0,1]上可能连续，也可能不连续.

[1]华东师范大学数学系.数学分析[M].北京：高等教育出版社, 2001.

[2]王高雄，周之铭，朱思铭，等.常微分方程[M].第三版.北京：高等教育出版社,1978.

[3]李文荣，张全信.函数方程与微分方程的解析解[J].北京：科学出版社,2008.

[4]Fleron,JF.A note on the history of the Cantor setand Cantor func⁃tion[J].Math Mag,1994（67）：136-140.

[5]杨晓玲.广义的Cantor函数的解析表示[J].云南大学学报（自然科学版）,2001，23（6）：417-421.

[6]陈其襄,张奠宙,魏国强,等.实变函数与泛函分析基础[M].第三版.北京：高等教育出版社,2003.

[7]周民强.实变函数论[M].北京：北京大学出版社,2001.

（编校：许洁）

Propertiesof Extended Cantor Function

JIANHuanyan,FUQiuju,ZHANGZhengliang
（CollegeofMathematics,Yinbin University,Yibin,Sichuan 644007,China）

The continuity,differentiability,integrability of extended Cantor function were discussed by characters of val⁃ues.The results show that the setofnon-differentiable points isa Cantor-like setin[0,1].

valueof function；continuity；differentiability；integrability；Cantor function

O174.1

A

1671-5365（2015）06-00121-04

2015-04-10修回：2015-04-27

2013年大学生课外科技活动项目“一类特殊函数的性态”（2013X113）；2013校级本科教学工程项目“基于竞赛、考研的问题探究式教学改革”（宜学校教〔2013〕291号）

蹇焕燕（1993-），女，本科生，数学与应用数学专业

张正亮（1973-），男，副教授，硕士，研究方向为泛函分析

网络出版时间：2015-04-27 17：18网络出版地址：http：//www.cnki.net/kcms/detail/51.1630.Z.20150427.1718.001.html

引用格式：蹇焕燕，付秋菊，张正亮.推广的Cantor函数的性质[J].宜宾学院学报,2015,15（6）：121-124.