施密特因子在镁合金微观变形机制研究中的应用
张士宏,宋广胜,徐勇,宋鸿武,程明
(中国科学院金属研究所,沈阳 110016)
自从奥地利学者施密特在1924年建立施密特因子的表达式以来[1],施密特因子以其计算简单、表述方便的优点,在金属塑性变形机制的分析中得到了广泛应用[2—5]。通过计算金属在简单变形中的施密特因子,可以定性分析各种位错滑移机制的启动趋势。
镁合金因其固有的密排六方(hexagonal closepacked,HCP)晶体结构,使其呈现明显不同于立方系晶体结构金属的塑性变形特点,具体表现为:镁合金中一些位错滑移模式的启动对温度极敏感[6],室温下变形,通常为基面滑移和拉伸孪晶启动,以满足密席斯准则[7];织构对镁合金宏观力学性能影响明显,从而引起宏观力学性能的各向异性;孪晶特别是拉伸孪晶在变形初期易启动,从而引起宏观力学性能拉压不对称性等特征。
金属塑性变形过程中,孪晶和滑移系的启动通常遵循施密特定律,即施密特因子大的微观变形模式先启动。对于某个具体的变形模式,其能否启动作为取决于该变形模式的临界剪切应力(critical shear stress,CRSS)和沿切变方向的施密特因子,对于镁合金的各种微观变形模式,拉伸孪晶的CRSS值最小,远低于柱面和锥面滑移系,但孪晶的启动具有单向性特点,即在晶粒取向和载荷方向确定的条件下,只能沿某单一方向进行切变,这一点不同于滑移系的启动特点。故对应孪晶的施密特因子取值范围为[-0.5,0.5],而对应滑移系的施密特因子取值范围则为[0,0.5]。相比于滑移系的启动,施密特因子在描述孪晶启动机制方面更具有优势,如可以定量地确定所启动的孪晶变体。
文中结合作者在镁合金塑性变形机理的研究工作,介绍了施密特因子在镁合金微观变形机理分析中的应用。
1 施密特因子的表述方法
向,t1~t6分别对应晶粒1的6个孪晶变体的取向,分别标示在t1~t6下面的数值则对应着6个孪晶变体的施密特因子值。图中显示拉伸孪晶变体t1和t5具有最大施密特因子而最有可能启动,而实际上孪晶变体t5与变形后晶粒1的取向一致,从而可以确定该变形过程中实际启动的孪晶变体为t5。在镁合金变形机理研究中,施密特因子分布的极图表示法多用于对单个晶粒孪晶启动机制的分析[8—10]。
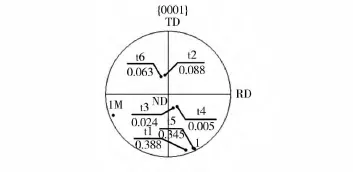
图1 镁合金试样中晶粒1的极图Fig.1 Pole figure of grain 1 in the magnesium alloy specimen
施密特因子适合于在单向载荷条件下对金属微观变形机制的描述,其最原始的表达方式为代数式:
m=cos φ·cos λ (1)
式中:m为施密特因子;φ为外载荷与滑移面法线的夹角;λ为外载荷与滑移方向的夹角。
在具体的应用中,在直角坐标系(x,y,z)下式(1)的计算式则为:
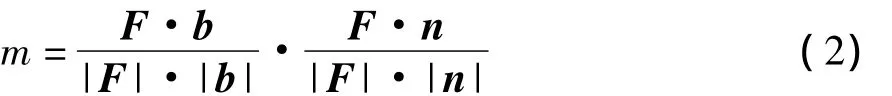
HCP晶体关于其C轴对称,在HCP晶体中,可以在1/12的空间中表示晶体的一些特征,图2显示了反极图表示变形镁合金试样内若干晶粒的基面滑移系的最大施密特因子分布。与图1所示的表示方法不同,施密特因子分布的反极图表示法多用于对观测区域内所有晶粒进行统计分析[11—12]。
式中:F为外载荷矢量;b为切变方向矢量;n为滑移或孪晶面的法线矢量。
上述公式可以对单个晶粒的某个滑移系或孪晶系的施密特因子值进行计算,但在实际应用中,需要借助于其他表达形式对晶粒中各变形模式的施密特因子进行表述,以便于分析金属塑性变形的微观机理。常用的施密特因子分布表述方法有极图表示法、反极图表示法、晶粒取向图表示法和特定坐标系表示法等。
图1显示了对于某个镁合金变形过程在极图中表述晶粒施密特因子的方法,在图示的{0001}极图中,1M和1分别表示晶粒1在变形前后对应的取

图2 镁合金压缩过程中最大施密特因子的分布Fig.2 Maximum Schmid factor distribution of Mg alloy during compression
施密特因子也可以在利用电子背散射衍射(E-lectron Backscatter Diffraction,EBSD)技术所测得晶粒取向图中表示,如图3所示,对于某个镁合金压缩后的试样,在EBSD扫描区域内,显示了该区域内晶粒的3个基面滑移系的施密特因子的分布。施密特因子分布的晶粒取向图表示法较为直观地显示观测区域内所有晶粒的施密特因子分布,在镁合金变形机理研究中,该方法多用于对滑移系的施密特因子分布进行分析[13—14]。

图3 变形区晶粒滑移系Fig.3 Schmid factor distribution of slips
针对 HCP晶体结构,可以建立特定坐标系,从而可以更准确地描述施密特因子在空间的分布。如图4a所示,建立(θ,β)坐标系,图4b和 c则分别显示了在该坐标系下,θ 值分别为0°,-15°和 -30°,而β值为0°~90°时的基面滑移系和柱面滑移系的施密特因子分布,图4d则显示了在β值为0°,而 θ值为 0°~90°时的施密特因子分布。
上述结果直观地显示了施密特因子的分布特征,对分析镁合金微观变形机制具有重要的参考作用。如图4b显示,当单向应力σ与C轴夹角为45°时,基面滑移系处于软取向而最易启动,并且基面滑移系的施密特因子分布关于β=45°对称分布。图4c则显示当β为90°时,即应力σ与C轴垂直时,柱面滑移系处于软取向而最易启动;而当β为0°时,即应力σ与C轴平行时,柱面滑移系处于硬取向而无法启动,并且柱面滑移系的施密特因子随着β角的增大而单调递增。
图4d则显示了当β为90°,即压应力σ与C轴垂直时,拉伸孪晶6个变体的施密特因子的空间分布特点。图中结果显示,6个孪晶变体的施密特因子分布可以分成3组,即变体1和5、变体2和6、变体3和4,孪晶变体的施密特因子分布呈现三角函数曲线特征。图4d直观地显示,当垂直于C轴的压应力位于θ=[-30°,30°]范围内时,孪晶变体1和5最易启动,在 θ=[-30°,-60°]范围内,孪晶变体3和4最易启动,而在 θ=[30°,60°]范围内,孪晶变体2和6最易启动。
2 施密特因子在镁合金微观变形机理分析中的应用
2.1 孪晶启动对变形模式的影响
在镁合金的各种微观变形模式中,拉伸孪晶因其CRSS最小而最易启动,启动拉伸孪晶对变形的直接贡献量较小,但其能够改变晶粒取向,从而有利于更多滑移系启动。
对于AZ31镁合金轧制板材,室温下沿轧向压缩变形,利用EBSD对晶粒取向变化进行原位跟踪,从而分析其微观变形机制。图5显示了在上述实验中所得拉伸孪晶启动对滑移系启动的分析结果[15],图5结果显示,在拉伸孪晶启动前后,基面滑移系的施密特因子虽然有小幅提高,但多数晶粒的施密特因子小于0.2而处于硬取向,即在拉伸孪晶启动前后基面滑移系的施密特因子变化不明显,始终处于硬取向。
图5c和d显示在拉伸孪晶启动后,柱面滑移系的施密特因子则明显降低,大约由0.3降至接近于0,即在孪晶启动后明显处于硬取向而不易启动。图5e和f显示在拉伸孪晶启动后,锥面滑移系的施密特因子大幅度增加,平均由0.25增至约0.45左右,即在拉伸孪晶启动后,锥面滑移系处于软取向而易启动。上述变形过程微观变形模式的定量模拟结果显示,在变形后期锥面滑移系大量启动,而CRSS值较小的柱面滑移系在变形后期启动量较少[15],这正是拉伸孪晶启动对不同滑移系的施密特因子影响差异明显的结果。
镁合金沿轧向压缩的各滑移系的最大施密特因子分布如图6a,b和c所示,图6d和e则分别显示了上述变形过程中,在拉伸孪晶启动前后观测区域内所有晶粒的压缩轴(即轧向)的分布。可以看出在拉伸孪晶启动前,对于基面滑移系,多数晶粒位于施密特因子较低区域;对于柱面滑移系多数晶粒则位于施密特因子较大的区域;而对于锥面滑移系多数晶粒则位于施密特因子稍大的区域。在拉伸孪晶启动后,图6e则显示,对于基面滑移系,多数晶粒还是位于施密特因子较低的区域;对于柱面滑移系,多数晶粒则位于施密特因子较低的区域;而对于锥面滑移系,多数晶粒则位于施密特因子最高区域。图6中所显示的拉伸孪晶启动前后各滑移系的施密特因子变化特点与图5所显示的结果一致,即拉伸孪晶的启动不明显改变基面滑移系的施密特因子值,明显降低柱面滑移系的施密特因子,而大幅增加锥面滑移系的施密特因子值。

图5 各晶粒滑移系在孪晶启动前后的施密特因子Fig.5 SFs of slps before and after twinning
2.2 孪晶变体分析
在AZ31镁合金轧制板材上截取立方体试样,对该试样先后沿轧向和横向压缩至一定变形量。图7则显示了在沿横向压缩变形后观测区内部分晶粒的取向及其对应的{0001}极图。图中的1M~6M则分别表示6个晶粒在沿横向压缩前(沿轧向压缩后)的取向,数字1~6则分别表示6个晶粒在沿横向压缩后的取向,极图中的t1~t6则分别表示每个晶粒对应的6个拉伸孪晶变体,其具体的晶体学特征如表1所示。
图7中每个晶粒的极图显示,在沿横向压缩后,所有晶粒的取向与孪晶变体t1或t5的取向最接近,表明在沿横向压缩过程中所有晶粒所启动的孪晶变体都为t1或t5,图4e中的结果显示,在θ=[-30°,30°]范围内孪晶变体t1和t5具有最大的施密特因子而最易启动,由图8所显示的试样沿轧向压缩后的{10}极图特征,可以看出此时沿横向(TD)压缩,则 θ角在[-30°,30°]范围内,即位于孪晶变体t1和t5具有最大的施密特因子的角度范围内,从而所启动的孪晶变体皆为t1或t5。

图6 各滑移系的最大施密特因子分布以及室温压缩过程中晶粒压缩轴在孪晶启动前后的分布Fig.6 Distribution of the maximum SFs of Slips and distribution of the com pression axes of grains before and after twinning during compression at rom temperature

图7 镁合金压缩试样中晶粒孪晶变体的启动Fig.7 Activation of twin variant within the compressed Mg alloy specimen
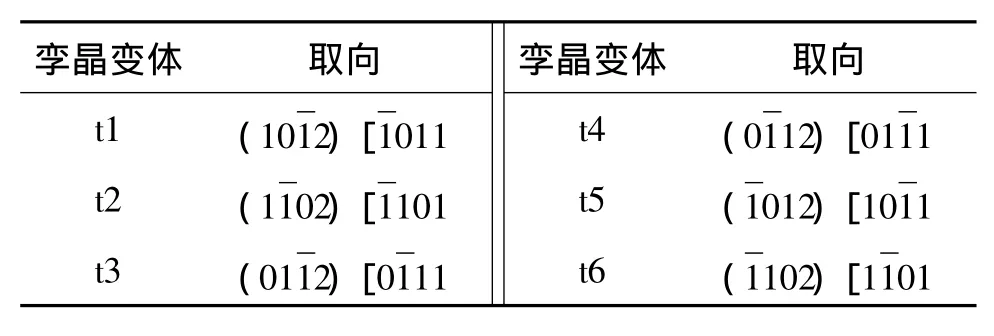
表1 镁合金的拉伸孪晶变体及其取向Table 1 Mg alloy twin variants and their orientations
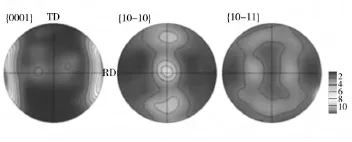
图8 镁合金试样沿轧向压缩后的极图Fig.8 Pole figures of Mg alloy specimen after compression along rolling direction
2.3 孪晶启动机制分析
对AZ31镁合金轧制板材室温下沿轧向进行拉伸,利用EBSD技术原位跟踪变形过程晶粒取向变化。图9显示了在不同变形量下观测区内部分晶粒的取向变化,其中晶粒15和16基体中出现了孪晶带。一些研究结果中也报道了在拉伸变形后的镁合金晶粒中产生了孪晶,但都推测是在试样拉伸后的卸载过程中产生的。
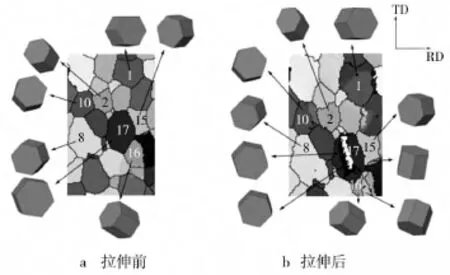
图9 晶粒在变形前后的取向图Fig.9 Grain orientation micrographs before and after deformation
表2显示了在拉伸变形过程中晶粒15和16的6个孪晶变体的施密特因子值,其中施密特因子值为负数的孪晶变体应该是在试样拉伸后卸载过程中启动。图10a则显示了实际启动的孪晶变体,可以看出,晶粒15中所实际启动的孪晶变体为[110],而表2显示该孪晶变体拉伸过程具有最大施密特因子,符合施密特定律,同样,晶粒16在拉伸变形过程中启动了具有最大施密特因子值的孪晶变体[110]。图10则显示了上述孪晶启动机制,即晶粒15和16的C轴与轧向(RD)的夹角较小,在拉应力作用下,晶粒沿C轴方向产生正应变,从而产生拉伸孪晶,使晶粒C轴与横向接近。
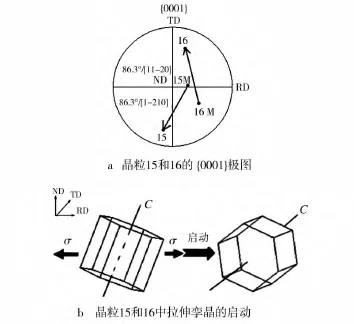
图10 晶粒15和16中孪晶的形成机制Fig.10 Mechanism of twin activation for grain 15 and 16
上述分析结果表明,拉伸试样中的一些晶粒内的孪晶是在试样拉伸变形过程中启动的,而非在卸载过程中启动。
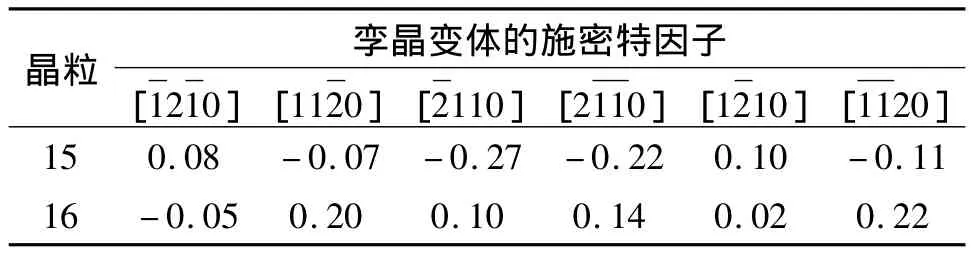
表2 试样拉伸过程中晶粒15和16的孪晶变体的施密特因子Table 2 Schmid factor of twin variant in grain 15 and grain 16 during the tension
3 结论
1)施密特因子有极图表示法、反极图表示法、晶粒取向图表示法和特定坐标系表示法等,相比于施密特因子的数值计算结果,上述各种表示法能够直观地表示变形过程中施密特因子的分布。
2)在镁合金塑性变形机理研究中,采用上述各种施密特因子表示法可以准确描述孪晶启动机制,及其对后续变形机制的影响。
[1]SCHMID E,BOAS W.Plasticity of Crystals[M].Berlin and London:Springer and Hughes,1950.
[2]刘毓舒,赵波,宓小川.泰勒模型在冷轧深冲钢塑性各向异性预估中的应用[J].上海交通大学学报,2000,34(3):326—328.
LIU Yu-shu,ZHAO Bo,MI Xiao-chuan.Application of Taylor Model in Prediction of Plastic Anisotropy for Cold-Rolled Deep Drawing Steel[J].Journal of Shanghai Jiaotong University,2000,34(3):326—328.
[3]陈建,李巍,彭渝丽,等.面心立方金属冷拔织构的计算机模拟[J].西安工业大学学报,2008,28(3):235—239.
CHEN Jian,LI Wei,PENG Yu-li,et al.Computer Simulation of Cold Drawing Textures[J].Journal of Xi'an Technological University,2008,28(3):235—239.
[4]WU Xian-ping,KALIDINDI S R,NECKER C,et al.Prediction of Crystallographic Texture Evolution and Anisotropic Stress-strain Curves During Large Plastic Strains in High Purity α-titanium Using a Taylor-type Crystal Plasticity Model[J].Acta Materialia,2007,55:423—432.
[5]KUO J C,CHEN D,CHEN S H,et al.Prediction of the O-rientation Spread in an Aluminum Bicrystal During Plane Strain Compression Using a DIC-based Taylor Model[J].Computational Science,2008,42:564—569.
[6]张士宏,宋广胜,宋鸿武,等.镁合金板材温热变形机理及温热成形技术[J].机械工程学报,2012,48(18):28—32.
ZHANG Shi-hong,SONG Guang-sheng,SONG Hongwu,et al.Deformation Mechanism and Warm Forming Technology for Magnesium Alloys Sheets[J].Chinese Journal of Mechanical Engineering,2012,48(18):28—32.
[7]JAIN A,AGNEW S R.Modeling the Temperature Dependent Effect of Twinning on the Behavior of Magnesium Alloy AZ31B Sheet[J].Materials Science and Engineering A,2007,462:29—36.
[8]SONG G S,ZHANG S H,ZHENG L,et al.Twinning,Grain Orientation and Texture Variation of AZ31 Mg Alloy during Compression by EBSD[J].Journal of Alloys and Compounds,2011,509:6481—6488.
[9]GODET S,JIANG L,LUO A A,et al.Use of Schmid Factors to Select Extension Twin Variants in Extruded Magnesium Alloy Tubes[J].Scripta Materialia,2006,55:1055—1058.
[10]HE J J,LIU T M,ZHANG Y,et al.Twin Characteristics and Flow Stress Evolution in Extruded Magnesium Alloy AZ31 Subjected to Multiple Loads[J].Journal of Alloys and Compounds,2013,578:536—542.
[11]PEI Y,GODFREY A,JIANG J,et al.Extension Twin Variant Selection During Uniaxial Compression of a Magnesium Alloy[J].Materials Science and Engineering A,2012,550:138—145.
[12]BARNETT M.Non-Schmid Behavior During Secondary Twinning in a Polycrystalline Magnesium Alloy[J].Acta Materialia,2008,56:5—15.
[13]LI N L,HUANG G J,ZHONG X X,et al.Deformation Mechanisms and Dynamic Recrystallization of AZ31 Mg Alloy with Different Initial Textures during Hot Tension[J].Materials and Design,2013,50:382—391.
[14]WU B L,ZHAO Y H,DU X H,et al.Ductility Enhancement of Extruded Magnesium Via Yttrium Addition[J].Materials Science and Engineering A,2010,527:4334—4340.
[15]SONG G S,CHEN Q Q,ZHANG S H,et al.Deformation Micro-mechanism for Compression of Magnesium Alloys at Room Temperature Analyzed by Electron Backscatter Diffraction[J].Materials and Design,2015,65:534—542.

