镁合金管材挤压变形动态再结晶流函数法研究
于宝义,郑黎
(沈阳工业大学,沈阳 110870)
因具有质轻、比强度高、比刚度高、尺寸稳定性好、电磁屏蔽能力强、生物可降解等特点,镁及镁合金的制备、加工和应用已成为目前材料、先进制造领域以及生物医学界的研究热点之一[1—2]。然而,目前镁合金产品主要以铸件为主,高性能的变形镁合金产品应用极少。其主要原因是镁合金室温塑性低,变形能力差,加工难度大,加工成本高;但经过塑性加工的镁合金在强度、塑性性能的可靠性等各方面都优于铸造合金[3],因此,开发研究镁合金的塑性加工技术是扩大镁合金应用的关键。金属挤压过程中可获得较大变形量,将其与细晶材料制备工艺相结合,可充分发挥两者的技术优势,达到高效低耗短流程地获取高性能挤压制品等目的[4]。通过挤压细化晶粒是高性能镁合金成形的有效方法。
热挤压是镁合金主要的塑性加工方法,热挤压过程中,由于镁合金具有较低的层错能,其滑移面上的全位错容易扩展、缠结而形成密度较大的网状位错结构,随着应变量的增加,局部位错密度增大引发动态再结晶。镁合金热变形过程中产生的动态再结晶,可以细化晶粒组织、减少缺陷,提高合金力学性能[5],因此动态再结晶是镁合金热变形过程中主要的软化机制以及改善合金组织和性能的重要手段[6]。对于动态再结晶发生的临界条件以及动力学理论与实验的研究具有重要意义。Poliak与Jonas通过应变硬化率与流变应力曲线上的拐点来确定动态再结晶临界应变εc,并建立了临界应变与变形条件之间的定量关系[7—8];黄光杰等人指出,AZ31镁合金初始动态再结晶的临界应变εc与峰值应力对应的应变εp之间满足关系εc=(0.4~0.6)·εp[9];基于 Avrami方程,QUAN[10],LIU[11],XU[12]分别给出了AZ81,AZ31B,AZ91D镁合金热变形过程中动态再结晶体积分数模型,模型中对于动态再结晶临界应变的定义均采用εc=kεp的形式。
对于动态再结晶的数值模拟研究一直都是热点课题,多数的模拟研究集中于变形局部的介观尺度模拟,如采用元胞自动机法[13—14]、蒙特卡罗法等[15],且取得了有价值的学术成果。进行介观尺度模拟往往需要简化加载边界条件,对于复杂的变形过程模拟精度会受到影响,且需要大量的计算时间,且仅能模拟局部的动态再结晶过程,不便于工程中对于任意工况中发生动态再结晶的临界部位以及动态再结晶分布等的模拟。流函数法是能量法的一种,应用流函数法解析塑性加工问题具有方便、灵活的特点,它易于建立满足复杂边界条件的运动许可速度场,有利于解析过程的范用化[16],它的理论计算值比较接近实际测量值[17—18],应用流函数法可以获得挤压变形区的应变、单位挤压力等理论数据[19]。本研究将通过流函数法建立镁合金管材挤压变形区的应变场模型,并结合热压缩实验研究镁合金管材挤压变形过程中动态再结晶的发生及分布规律。
1 应变速率、应变场流函数法求解模型


图1 流函数速度矢量示意图Fig.1 Velocity vector schematic of flow function
管材挤压过程中,材料的变形主要集中在挤压锥杯内。如图2所示,R1为挤压筒的半径;R2为挤压出口的半径;R0为挤压针的半径;v0为冲头速度;vr2为进入圆弧面的速度;vr1为挤压出口速度,锥杯半角记为β。假设:材料进入挤压变形区是以r2为半径的一个圆弧面,其初始速度v0与坐标z反向,进入圆弧面的速度vr2,假设在圆弧面上所有vr2都指向圆心O'。R*为变形区内任一z坐标处模面坐标。R*=f(z)。通过z轴的流函数只与θ角有关,即φ=φ(θ),则一组流面函数ψ则是与模面一致的形状函数。挤压锥杯模面上,流函数满足:

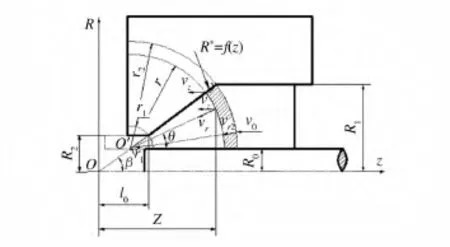
图2 管材挤压示意图Fig.2 Schematics of tube Extrusion
根据秒流量相等的原则,即通过r2为圆弧面流量Q2与通过半径为r弧面流量Q相等。通过半径r,r2的弧面曲线方程分别为:

相应的回转弧面积为:

根据秒流量相等可得径向速度:

从而可得到轴向速度为:

根据前文假设,挤压锥杯内流函数为:

根据式(1)即可计算应变速率张量:

设在与挤压力成一角度的斜截面上,该斜截面上其法线方向与挤压力作用方向的夹角为β,在该斜截面上剪切应变速率与挤压力作用方向的夹角为θ,当θ=β=45°时斜截面上剪切应变速率最小,也就是最小切变理论模型。
计算斜截面剪切应变速率应首先计算斜截面上全应变速率,再计算法向应变速率。该斜截面上的剪切速率与全应变速率满足:

式中:e为斜截面上的全应变速率,设材料变形满足Levy-Mises本构方程,则斜截面上的全应变速率也可按照求解斜截面上的全应力的方法计算,即:

当 θ=β=45°时,n1=(/2,0,),nk=(/2,0,/2)则斜截面上的法向应变速率为:

则剪切应变速率为:

设在挤压筒内一质点微小的位移u0,由于挤压速度是一定的,当挤压速度为v0时,可求得u0在挤压杯内挤出的时间t,再将时间与求得的应变速率的乘积除以v0即为所求的应变场。则挤压锥杯内的剪切应变可表示为:

2 动态再结晶临界条件
本研究通过热模拟试验测得了AZ91D镁合金热压缩变形真实应力-应变曲线(如图3所示),并利用所得力学性能数据建立AZ91D镁合金动态再结晶的临界条件。压缩式样尺寸为φ8 mm×15 mm,压缩温度分别673,693 K;压缩应变速率为0.1,0.01,0.0033,0.001 s-1。
由等温压缩所得到的真实应力-应变曲线可以看出,在653,673 K压缩AZ91D镁合金试样时,流变应力曲线上均呈现出明显的峰值特征,说明在实验条件下材料发生了动态再结晶软化。一般来说,动态再结晶需要一个临界变形量,只有当实际变形量超过临界变形量时,动态再结晶才会发生。与静态再结晶相比,动态再结晶所需的临界变形量一般更大。通常认为,应力-应变曲线上出现峰值预示着动态再结晶的发生。然而,事实上动态再结晶在应变未达到峰值应力对应应变时就已经发生[7—8]。为确定初始动态再结晶的临界条件,E.I.Poliak和J.J.Jonas提出了基于热力学不可逆原理的动力学临界条件,即认为临界条件与应变硬化率-应变曲线上的拐点相对应。以此确定的门槛应变值即为临界应变。式(17)为应变硬化率Θ的计算式。

图3 两种温度下的真应力应变曲线Fig.3 True stress-truestrain at different tempertature

利用式(17)可计算得出镁合金AZ91D热压缩时发生动态再结晶的临界应变εc,表1为在不同应变速率和变形温度下产生动态再结晶的临界应变。
根据表1可得到发生动态再结晶临界应变与应变速率和变形温度的函数关系:

到此,前文已通过流函数法建立了管材挤压过程中挤压锥杯内剪切应变场,再结合式(18)即可建立镁合金热挤压过程中锥杯内发生动态再结晶的判定准则:γ-εc=0时为初始动态再结晶临界值;当γ-εc<0则不能发生动态再结晶;当γ-εc>0时,发生动态再结晶(γ见式(16))。

表1 在不同应变速率和变形温度下产生动态再结晶临界应变Table1 The critical strain appeared DRX at different temperature and strain rate
3 模型算例及实验验证与分析
3.1 流变函数模型算例
根据上文采用流函数法建立的镁合金管件带锥角挤压变形区内,任意质点的应变速率场数学模型与发生动态再结晶的临界判据,编程并计算绘制了在挤压速度为1 mm/s时,管材挤压过程中锥杯变形区内的剪切应变分布图、动态再结晶分布图以及动态再结晶临界部位分布图,如图4、图5所示。其中横坐标为图2中R,纵坐标为图2中θ;图4中不同的颜色代表锥杯中不同的切应变值γ;图5中不同的颜色表示不同的γ-εc值。

图4 挤压锥杯内的切应变场Fig.4 Shear strain field of extrusion taper cup
由图4可看出,挤压锥杯内靠近挤压针的变形最为剧烈,而靠近挤压筒一侧的变形则较小,锥杯内整个应变场的分布趋势是随着距离挤压针的距离的减小,变形层度逐渐增大。从纵向来看,挤压变形从上到下(锥杯上部到挤压出口)越来越剧烈。此过程变化说明,虽然挤压过程是整块坯料都参与变形,但变形最大部分是靠近挤压针部分的坯料,而变形较弱的部分是靠近挤压锥杯部分的坯料。镁合金中动态再结晶的发生与应变状态密切相关,变形过程中应变越大,温度越高的部位将越易发生动态再结晶,从图5可看出,653 K时挤压锥杯内发生动态再结晶的部位在R约为57 mm的区域内,673 K时在R约为56 mm的区域内。与应变场分布一致,越靠近挤压针的区域其γ-εc值越大,说明越容易发生动态再结晶,从而可以推断在挤压过程中越靠近挤压针的区域,其动态再结晶发生越多、越充分。

图5 653,673 K温度下挤压锥杯内动态再结晶分布Fig.5 18 Distribution of DRX at 653 K and 673 K
3.2 实验验证及分析
为验证结合流函数法建立的镁合金管材挤压变形区的动态再结晶数学模型,进行了镁合金管材挤压实验,并对挤压锥杯内的镁合金进行了分区组织观测。实验中挤压温度为400℃,挤压比为18,挤压速度为1 mm/s,挤压坯料为圆筒状,内径40 mm,外径110 mm。挤压完成后根据图6所示区域划分分别截取挤压杯内材料进行组织观测,如图7所示为各区域组织图片。

图6 挤压杯内各部位示意图Fig.6 Schematic of each position in extrusion taper cup
图6中左侧位置1-6是挤压锥杯内靠近挤压针一侧的组织,右侧位置11-66是靠近挤压杯锥面一侧的组织。挤压变形从上到下(1到6或11到66)越来越剧烈,因此,晶粒理论上应该越来越细小。随着变形程度的增加,在挤压坯锭从原始铸造组织发展到有微小的变形(变形量约为 εr=-5.45%,εθ=-5.45%,εz=10.908%),在位置 1及11处上产生动态再结晶的趋势。如图6a,b是挤压锥杯中镁合金靠近挤压针位置1和靠近挤压锥杯面位置11偏下部位的纵断面组织,从图6中可以看出明显的分界,左下角的组织趋近于铸态组织是靠近挤压筒的部位,是材料刚进入挤压杯一段距离约3 mm处(变形量约为εr=-5.45%,εθ=-5.45%,εz=10.908%),枝晶生长发达,组织粗大,第二相分布于晶内和晶界处,该处没有发生动态再结晶;而右上角的组织由于发生变形的原因较细小,这是由于该处出现了明显的动态再结晶,并且有分界线。分界线是由铸态组织晶界构成的,其形状呈圆弧状。该部位恰恰是挤压杯内的应变与产生初始动态再结晶临界应变基本相同的位置,与上文计算的动态再结晶在挤压杯内的分布规律吻合,证明了本模型的正确性。
位置2和22处,变形量约为εr=-14.45%,εθ=-14.45%,εz=28.9%时,如图 6c,d,比较细小的动态再结晶晶粒数量开始逐渐增加,初生α镁基体被挤扁,或被挤碎。动态再结晶晶粒都出现在晶界处,同时发现有孪晶产生。当变形量继续增大(变形量约为εr=-23.45%,εθ=-23.45%,εz=46.9%)到图6e,f所示位置3和33处时,初生α镁基体大部分被挤碎,已经开始在晶界处产生大量的动态再结晶晶粒,还有被拉长的原始α基体组织存在,动态再结晶晶粒分布于被挤压拉长的晶界周围。当变形达到图5g,h所示位置4和44处时(变形量约为 εr=-32.45%,εθ=-32.45%,εz=64.9%),被拉长的初生α基体组织全部被挤碎,动态再结晶晶粒分布于被挤碎的晶界周围。
当变形达到位置5,55(变形量约分别为εr=-41.45%,εθ=-41.45%,εz=82.9%)和位置 6,66(变形量约分别为 εr=-50%,εθ=-50%,εz=100%)时,随着变形量增大到接近挤压出口处时,原始α基体组织全部被动态再结晶晶粒取替。晶粒比较细小均匀,如图 6i,j,k,l所示。
在挤压温度相同的情况下,变形程度起到关键作用,为获得高力学性能的挤压管件,选择变形量或挤压比是很重要的,尽可能保证出现均匀的动态再结晶晶粒,又不能使晶粒过于长大,从而达到细化晶粒,均匀组织,提高镁合金的综合力学性能的目的。

图7 挤压杯内各部位动态再结晶组织Fig.7 DRX microstructure of every position1 in extrusion taper cup
4 结论
1)应用流函数法建立了镁合金管件带锥角挤压变形区内任意质点的应变速率场数学模型、剪切应变速率模型以及应变场模型。
2)结合流变函数法建立的应变场模型与热模拟实验数据,建立了AZ91D镁合金管件带锥角挤压变形区内任意质点发生初始动态再结晶判据,并作出了挤压锥杯内动态再结晶分布图。
3)通过对挤压过程中挤压杯内各部位动态再结晶演变规律,分析发现在挤压变形达到5%左右,开始发生动态再结晶,动态再结晶的分布与所建立的计算模型结果相吻合。挤压变形过程初期晶粒被挤碎与产生动态再结晶同步进行,当变形量继续增大时,全部产生动态再结晶晶粒。
[1]丁文江,吴玉娟,彭立民,等.高性能镁合金研究及应用的新进展[J].中国材料进展,2010,29(8):37—45.
DING Wen-jiang,WU Yu-juan,PENG Li-min,et al.Research and Application Development of Advanced Magnesium Alloys[J].Materials China,2010,29(8):37—45.
[2]于宝义,吴永广,何淼,等.超细薄壁镁合金管材挤压成形工艺及微观组织[J].热加工工艺,2008,37(7):43—46.
YU Bao-yi,WU Yong-guang,HE Miao,et al.Forming Process and Microstructure of Superfine Thin Wall Magnesium Alloy Extrusion Tubes[J].Hot Working Technology,2008,37(7):43—46.
[3]陆国桢,王强,张治民,等.镁合金挤压成形技术的研究进展[J].热加工工艺,2012,41(15):86—94.
LU Guo-zhen,WANG Qiang,ZHANG Zhi-min,et al.Research and Development on Extrusion Forming Technology of Magnesium Alloy[J].Hot Working Technology,2012,41(15):86—94.
[4]李峰,石文勇,武英博,等.金属挤压成形技术研究与应用进展[J].精密成形工程,2014,6(5):45—49.
LI Feng,SHI Wen-yong,WU Ying-bo,et al.Developments in Researches and Application of Metal Extrusion Forming.Journal ofNetshape Forming Engineering,2014,6(5):45—49.
[5]AL-SAMMAN T,GOTTSTEIN G.Dynamic Recrystalliztion during High Temperature Deformation of Magnesium[J].Material Science and Engineering A,2008,490(1-2):411—420.
[6]陈先华,汪小龙,张志华.镁合金动态再结晶的研究现状[J].兵器材料科学与工程,2013,36(1):148—152.
CHEN Xian-hua,WANG Xiao-long,ZHANG Zhihua.Research Status of Dynamic Recrystallization of Magnesium Alloy[J].Ordnance Material Science and Engineering,2013,36(1):148—152.
[7]POLIAK E I,JONAS J J.A One-parameter Approach to Determining the Critical Conditions for the Initiation of Dynamic Recrystallization[J].Acta Materialia,1996,44(1):127—136.
[8]POLIAK E I,JONAS J J.A Initiation of Dynamic Recrys-tallization in Constant strain Rate Hot deformation[J].ISIJ International,2003,43(5):684—691.
[9]黄光杰,钱宝华,汪凌云,等.AZ31镁合金初始动态再结晶的临界条件研究[J].稀有金属材料与工程,2007,36(12):2080—2083.
HUANG Guang-jie,QIAN Bao-hua,WANG Lin-yun,et al.Study on the Critical Condition for Initial Dynamic Recrystallization of AZ31 Magnesium Alloy[J].Rare Metal Materials and Engineering,2007,36(12):2080—2083.
[10]QUAN Guo-zhen,SHI Yu,WANG Yi-xin,et al.Constitutive Modeling for the Dynamic Recrystallization Evolution of AZ80 Magnesium Alloy Based on Stress-strain Data[J].Material Science and Engineering A,2011,528:8051—8059.
[11]LIU Juan,CUI Zhen-shan,RUAN Li-qun.A New Kinetics Model of Flow Stress Characterizing Dynamics Recrystallization for Magnesium Alloy AZ31B[J].Material Science and Engineering A,2011,529:300—310.
[12]XU Yan,HU Lian-xi,SUN Yu.Dynamic Recrystallization Kinetics of As-cast AZ91D Alloy[J].Transactions of Nonferrous Metals Society of China,2014,24:1683—1689.
[13]HE Yi-zhu,DING Han-lin,LIU Liu-fa,et al.Computer Simulation of 2-D Grain Growth Using a Cellular Automata Model Based on the Lowest Energy Principle[J].Materials Science and Engineering A,2006,429:236—240.
[14]卢瑜,张立文,邓小虎,等.纯铜动态再结晶过程的元胞自动机模拟[J].金属学报,2008,44(3):292—296.
LU Yu,ZHANG Li-wen,DENG Xiao-hu,et al.Modeling Dynamic Recrystallization of Pure Copper Using Cellular Automation Method[J].Acta Metallurgica Sinica,2008,44(3):292—296.
[15]佟铭明,莫春利,李殿中,等.纯铜动态再结晶的Monte carlo法模拟[J].金属学报,2002,38(7):745—749.
TONG Ming-ming,MO Chun-li,LI Dian-zhong,et al.Simulation of the Dynamic Recrystallization of Pure Copper Using Monte Carlo Method[J].Acta Metallurgica Sinica,2002,38(7):745—749.
[16]王振范,木内学.三维流函数法解析在塑性加工中的应用[J].哈尔滨工业大学学报,2000,32(5):93—96.
WANG Zhen-fan,MANNABU Kiuchi.Application of 3D Fluxional Function to Metal Forming[J].Journal of Harbin Institute of Technology,2000,32(5):93—96.
[17]汪家才.金属压力加工的现代力学原理[M].北京:冶金工业出版社,1991.
WANG Jia-cai.Modern Metal Pressure Processing of Mechanics[M].Beijing:Metallurgical Industry Press,1991.
[18]杨海波,汪家才,刘光涛.金属压力加工问题的流函数速度模式上限解[J].北京科技大学学报,1994,18(增刊2):86—90.
YANG Hai-bo,WANG Jia-cai,LIU Guang-tao.Upper-bound Solution of Metal Forming Problem with the Flow Function Velocity Model[J].Journal of University of Science and Technology Beijing,1994,18(Suppl 2):86—90.
[19]毛艺伦,张清东,孙朝阳.高温合金管材挤压变形及挤压工艺的流函数法研究[J].北京科技大学学报,2011,33(4):449—454.
MAO Yi-lun,ZHANG Qing-dong,SUN Chao-yang.Study on Extrusion Forming of Superalloy Tubes by Flow Function Method[J].Journal of University of Science and Technology Beijing,2011,33(4):449—454.

