AZ31镁合金板材气体胀形的模拟及成形极限的预测

周国伟，李大永，彭颖红

（1.上海交通大学机械与动力工程学院，上海 200240;2.机械系统与振动国家重点实验室，上海 200240）

板材成形极限图（FLD）可以描述板材成形过程中复杂的变形情况下的极限应变值，是评价板材成形性能的重要依据。成形极限图通常采用球形凸模的胀形实验来获得［1—2］。气体胀形实验在航空制造领域被广泛采用，也可以被用作评估板材的成形性能，通过改变模具的长宽轴比，可以获得位于双拉测的成形极限［3—4］。与普通球头胀形相比，气体胀形可以极大地减小试样与板材之间的摩擦力，更有利于成形。通常气体胀形实验仅能获得平面应变右侧的FLD。最近，研究者将气体胀形实验扩展到了可以获得拉压侧成形极限［5—6］。

文中采用有限元方法，对前期高温下气体胀形实验进行仿真，采用对应变历史二阶导数分析的方法［7］，计算得到不同路径下的成形极限，并与实验结果进行比较。

1 板材材料参数

在300℃下，AZ31不同应变率下的单向拉伸结果如图1所示。由于动态再结晶的发生导致AZ31的单向拉伸曲线发生明显的下降，而且在300℃下，AZ31表现出明显的应变率敏感。AZ31其他的材料参数:密度、弹性模量和泊松比，分别设定为1.79×103kg/m3，45 GPa 和0.35。

图1 FE仿真材料曲线输入Fig.1 The stress strain data as input

图2所示为2种温度下3个方向的r值（厚向异性参数）随应变增加的变化趋势。通过对r值及面内3个方向RD，45°和TD方向应力应变曲线的比较，可以看到随着温度的升高，AZ31的各向异性逐渐减弱，而在300℃时，r值已经接近1，说明材料已经比较接近各向同性。通过将Naka［8］的实验结果与Mises及Hill48屈服面进行比较（见图3），可以看到在Mises及Hill48的表现非常接近，在TD单拉到等轴双拉区间，2种屈服准则都与实验数据拟合较好，而在等轴双拉到RD单拉区间，2种屈服准则与实验数据都有一定的偏差。文中采用Mises屈服准则，可以较好地描述材料的性能。

图2 r值随应变及温度的变化趋势Fig.2 Variation of r values with different strains and temperatures

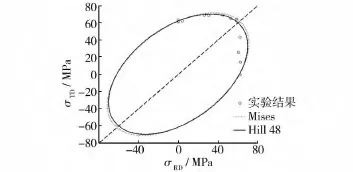
图3 AZ31在300℃下屈服的实验结果同Mises及Hill48屈服面的比较Fig.3 Comparison of the experimental yield result of AZ31 at 300℃with the Mises and Hill48 yield surface

2 气体胀形及建模

图4为实验过程的示意图。这里仅对实验的过程进行简单介绍，具体可以参考文献［6］。实验开始时，将试样放入加热炉中，压边圈下降夹紧试样，气体通过底部的管道输入，试样变形直到破裂。通过改变模具的长轴与短轴之比，可以得到右侧不同加载路径的极限应变值，文中采用的是4∶1，2∶1，4∶3，1∶1等4种比例。对于左侧的情况，通过采用双层板胀形的方法，上层板加工有不同间距的槽（分别为10，25，50 mm），而下层驱动板为同样材料的完整板，变形过程中底部板驱动上层板进行变形。采用这种方法可以得到气体胀形下，完整的成形极限图。

图4 气体胀形实验的示意图Fig.4 Schematic diagram of gas bulging experiment

根据实验情况，在Abaqus软件中仅建立1/4模型以提高计算效率，如图5所示。模具与试样之间摩擦因数设定为0.15，而在双层试样模拟中，试样之间的摩擦因数设定为0.2。压边力设定为50 kN，试样的中心边界对称边界条件，在试样的中心区域施加均匀分布的压力，并以0.03 MPa/s的速度线性增长。为了考虑应变率的影响，采用dynamic implicit求解器进行计算。

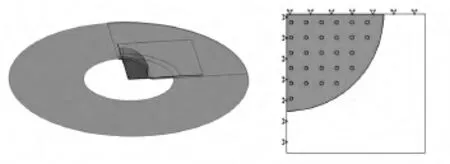
图5 模型中施加的对称边界条件及施加压力载荷区域Fig.5 Pressure loading of the sheet specimen and the boundary condtions，symmetry boundary conditions，and pressure loading of the sheet specimen region located in the die opening region

采用由Situ提出的二阶主应变转折点颈缩准则［7］，分析变形过程中应变最集中的区域，计算主应变的一阶导数及二阶导数（应变加速度），当二阶导数达到极大值时，此转折点认为局部颈缩已发生。图6分别是25 mm单层及双层10 mm的分析过程及结果。图中圈出的单元为选作应变历史分析的单元。

图6 GBF仿真结果Fig.6 Results of FE simulations of GBF

3 仿真结果与分析

图7为不同几何尺寸试样模拟的结果。通过有限元仿真及应变历史分析方法，可以得到除靠近平面应变尺寸的，其他所有极限应变。而在实验中靠近平面应变的极限应变也是很难得到的，如图8所示。通过比较单拉及平面应变情况下的最终试样，可以看到，在单拉情况下，应变集中出现在槽的外侧边缘（如圈所示），中间测量区域不受影响继续变形到颈缩;而在平面应变情况下，应变集中出现在槽的内侧边缘，即应变测量区域的边缘，而中间区域变形则受到抑制，导致中间区域变形较小。2种不同的变形情况，仿真与实验结果都吻合的很好。

图7 不同几何尺寸试样变形后结果Fig.7 Simulation results of specimens of different geometries after deformation

图8 实验结果及对应的仿真结果Fig.8 Experimental results and the corresponding simulation results

图9为不同加载路径下得到的预测极限应变与实验结果的比较，图9b为300℃下RD与TD方向FLD的比较，可以看到在300℃下两者比较类似，仅在平面应变到等轴双拉之间有较大的偏差，再次证明在300℃下，AZ31各向异性已经非常弱。通过比较FE仿真结果与TD（9d）及RD（9d）方向的实验结果，可以看到，计算结果同TD方向的FLD形状更为接近，这也应对了Mises屈服准则在TD与等轴双拉之间实验数据拟合，较RD与等轴双拉之间更好。

图9 仿真计算得到的FLD与实验结果的比较Fig.9 Comparison between the FLD calculated by simulation and the experimental results

4 结论

通过对300℃下AZ31镁合金气体胀形过程仿真，对应变历史进行分析，得到了不同加载路径下的极限应变值，并与实验结果进行了比对，分析了变形过程中应变的分布变化，并讨论了实验中不同几何尺寸试样的结果差异。

［1］NAKAZIMA K，KIKUMA T，HASUKA K.Study on the Formability of Steel Sheets［J］.Yawata Technical Report，1968，264:141—154.

［2］HECKER S S.Simple Technique for Determining Forming Limit Curves［J］.Sheet Met.Ind，1975，52:671—676.

［3］BARNES A J.Industrial Applications of Superplastic Forming:Trends and Prospects［J］.Mater Sci Forum，2001，357-359:3—16.

［4］LUO Y，MILLER C，LUCKEY G，et al.On Practical Forming Limits in Superplastic Forming of Aluminum Sheet［J］.J Mater Eng Perform，2007，16:274—283.

［5］BANABIC D，LAZARESCU L，PARAIANU L，et al.Development of a New Procedure for the Experimental Determination of the Forming Limit Curves［J］.CIRP Annals-Manufacturing Technology，2013，62:255—258.

［6］MITUKIEWICZ G，ANANTHESHWARA K，ZHOU G，et al.A New Method of Determining Forming Limit Diagram for Sheet Materials by Gas Blow Forming［J］.J Mater Process Technol，2014，214:2960—2970.

［7］SITU Q，JAIN M K，METZGER D R.Determination of Forming Limit Diagrams of Sheet Materials with a Hybrid Experimental-Numerical Approach［J］.Int J Mech Sci，2011，53:707—719.

［8］NAKA T，UEMORI T，HINO R，et al.Effects of Strain Rate，Temperature and Sheet Thickness on Yield Locus of AZ31 Magnesium Alloy Sheet［J］.J Mater Process Technol，2008，201:395—400.