基于遍历函数型数据下条件分位数的渐近性质

陈灵昕， 凌能祥， 王 娟， 杨 艳

（合肥工业大学 数学学院，安徽 合肥 230009）

众所周知，相比于条件均值，条件分位数不易受异常值影响，对其统计推断是非参数统计的重要问题之一，受到很多学者的关注。在解释变量X取值于半度量空间F，响应变量Y取值于R，来自总体（X，Y）的样本是相互独立或者某种相依场合下，文献［1］研究了在一些正则条件下，条件分位数估计的强相合性和渐近正态性；文献［2］在研究条件经验过程中给出了条件分位数的渐近正态性及条件分布函数的置信区间；文献［3］研究了基于双核和局部连续核方法的2个条件分位数非参数估计的相合性和渐近性质。

近年来，函数型数据分析已成为数理统计研究的主要领域之一。函数型数据被看作连续时间随机过程的一条样本轨道，其取值于一个无限维函数型空间，函数型数据的非参数估计的理论和方法的研究在近几年也得到广泛的发展，如文献［4］利用核方法系统地研究了非参数回归算子、累积分布函数等估计量的几乎完全收敛速度，并在α－混合的相依场合下推广了上述结果；文献［5］研究了函数型非参数模型的稳健估计，并在i.i.d.场合下给出了非参数回归函数稳健估计量的几乎完全收敛。

基于函数型数据下分位数的非参数估计也引起了学者们的广泛关注，文献［6－7］分别研究样本在i.i.d.和α－场合下，条件分位数核估计量的渐近正态性；文献［8］采用了推广的L1方法构建样本在i.i.d.场合下条件分位数非参数估计量的相合性以及渐近性质；文献［9］利用N－W双核估计方法研究了样本在相依场合下，条件分位数核估计的LP范数收敛及收敛速度。

遍历性假设是在统计物理学、热力学和信号处理中的基本假设。尽管α－混合正在最常见的混合条件中是最弱的，但它还不能包括所有的相依结构，另一方面，要验证一个非线性时间序列是否为α－混合也不是件容易的工作，而时间序列数据遍历性验证则比较方便，参见文献［10］；并且遍历性假设在实际中也有很重要的应用，比如它是统计物理学中控制关于气体、原子、电子、等离子等热力学性质的基本条件之一。

为了更好地阐述本文内容，假设（Xi，Yi）1≤i≤N为一组平稳遍历函数型样本，Yi为取值于实数空间R的随机变量，Xi为取值于半度量空间（F，d（·，·））的随机变量。给定x∈F时y的条件累积分布函数为：

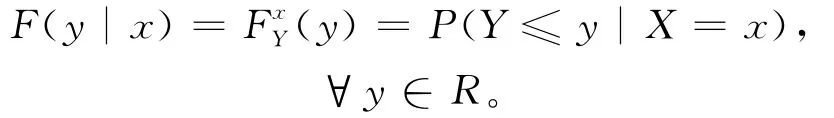
条件累积分布函数F（·｜x）的α分位数为：

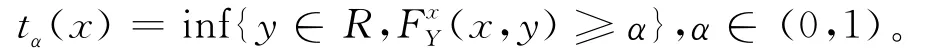
根据文献［4］得到条件累积分布函数的N－W双重核估计为：

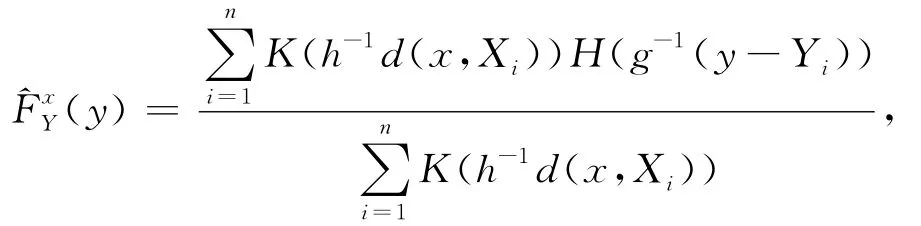
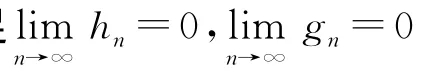
则函数型条件分位数tα（x）的核估计为：

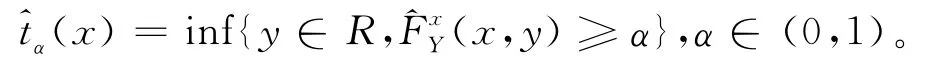
最近，文献［11］考虑了在遍历函数型数据条件下，利用经典的N－W核估计方法研究非参数回归算子估计量的渐近性质，如渐近正态性、相合性；文献［12］同样在遍历函数型数据下利用N－W核估计方法研究非参数回归算子估计量的强逐点收敛速度及一致收敛速度；文献［13］在遍历条件下利用稳健M－估计方法研究非参数回归算子估计量的几乎完全收敛速度；文献［14］在遍历函数型数据下利用鞅的中心极限定理研究条件分位数核估计的渐近性质。本文是在现有文献基础上，基于遍历函数型数据，利用双核估计方法研究条件分位数估计量的逐点收敛速度，推广了现有文献中的结果。

1 基本假设和主要结果

1.1 基本假设

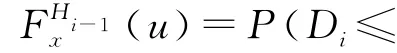
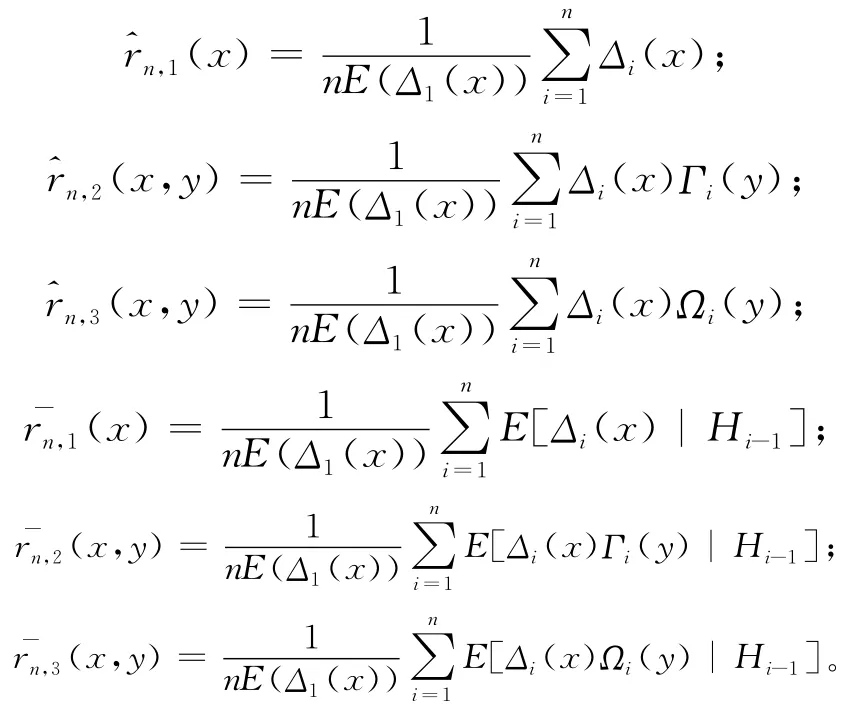
其中

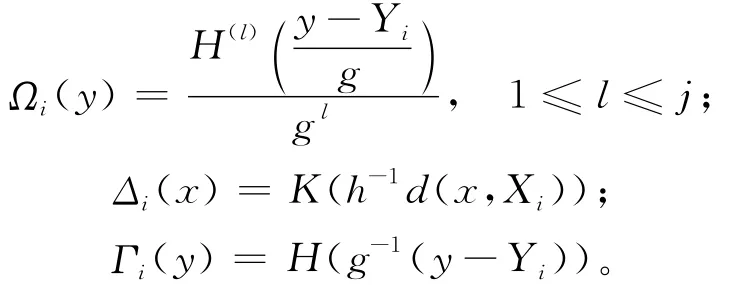
为了证明本文的主要结论，给出一些基本假设。

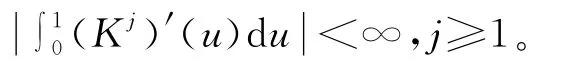
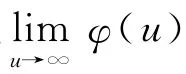
（3）给定δ－域Ai－1，Γi（y）、Ωi（y）的条件期望只取决于Xi，即E（Γi（y）｜Ai－1）＝E（Γi（y）｜Xi）a.s.，E（Ωi（y）｜Ai－1）＝E（Ωi（y）｜Xi）a.s.，且对∀m≥2有：

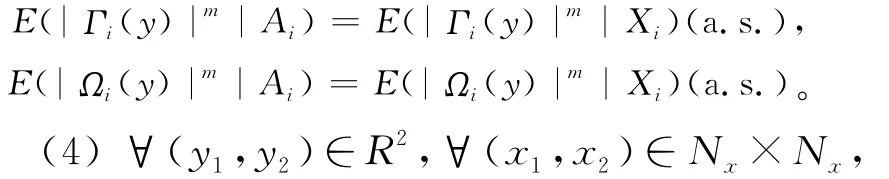
则有：

其中，l＝1，…，l；C＞0；β1＞0；β2＞0；为严格单调递增的分布累积函数。

（5）∀u＞0，P（X∈B（x，u））＝φx（u）＞0。

假设（1）是研究非参数函数型数据估计量的一般条件；假设（2）是遍历型数据的特有条件，此条件参见文献［12］，满足条件随机过程的例子同样参见文献［12］；假设（3）是本文证明过程中所需要的关键条件，此条件参照文献［12，14］；假设（4）是研究分布函数的经典条件；假设（5）是对小球概率的限制。

1.2 主要结论

定理1 若假设（1）～假设（5）成立，并且对∀l＝1，…，j，当n→∞，且对∀p≥2的自然数有：

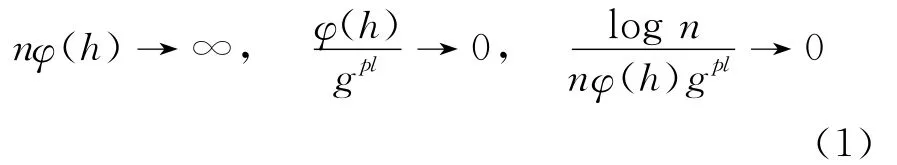
那么∀x∈F时有：

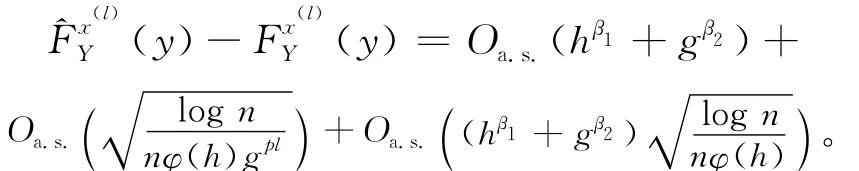
定理2 假设函数（·）在tα（x）处j次连续可微，且满足：

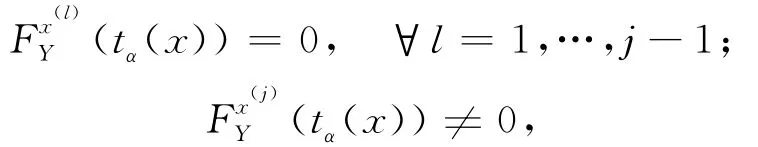
核函数H是j次连续可微，假设（1）～ 假设（5）成立，则有：

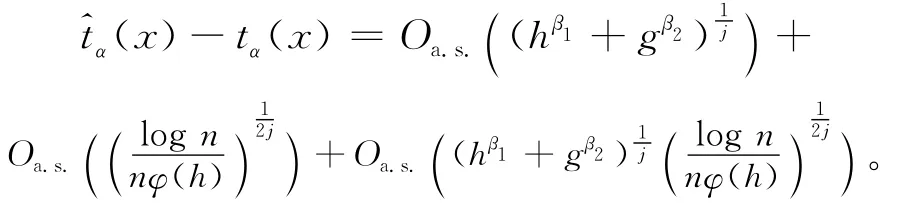
2 若干引理及定理的证明

为了证明定理1，先做分解，对∀x∈F，有

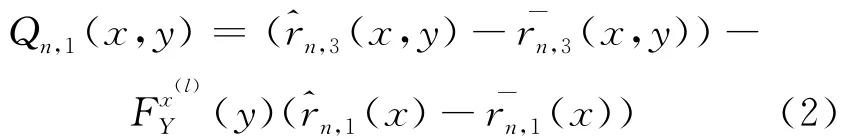
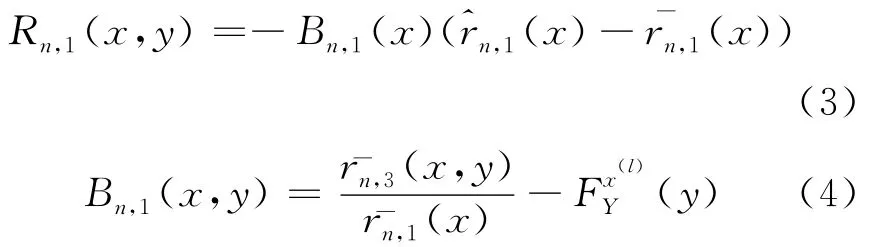
则有：

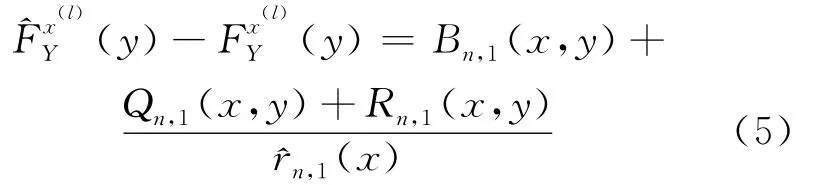
引理1 假设（1）～假设（4）、（1）式成立，则对∀x∈F有：

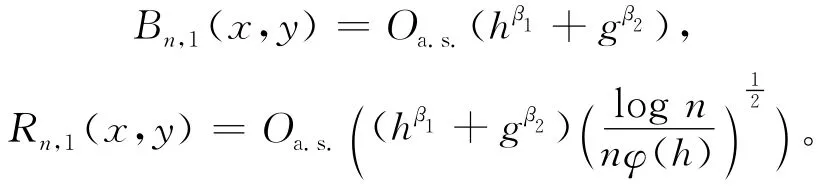
证明

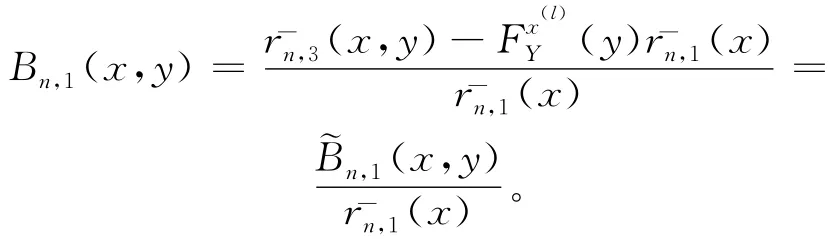
其中

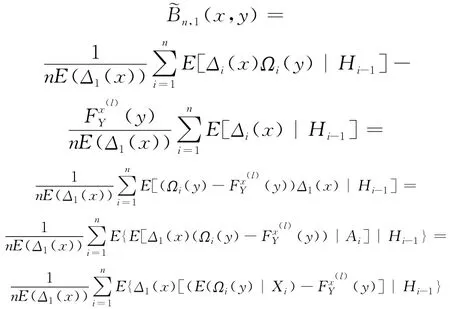
其中

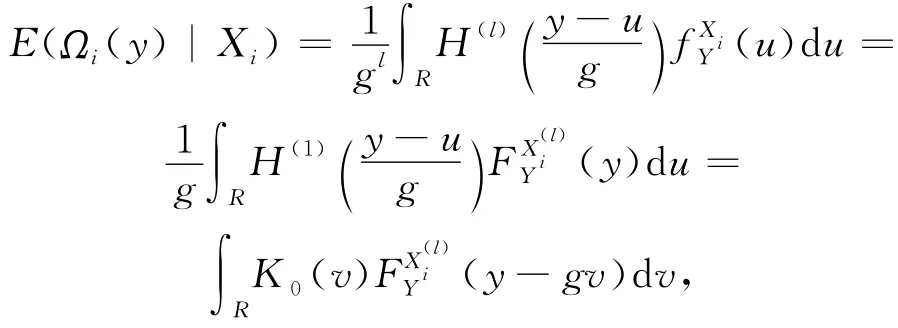
故

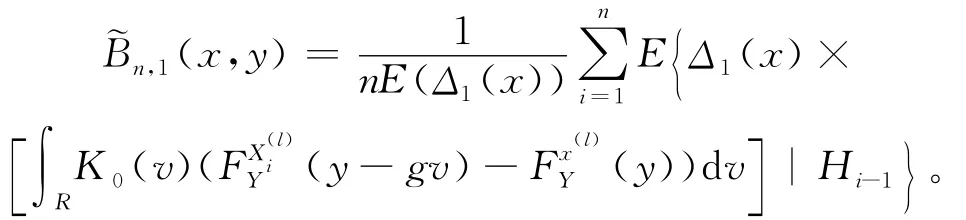
由假设（4）得：

由文献［12］中引理2，假设（2）中的② 、③ 可知E［Δ1（x）｜Hi－1］是有界量，则

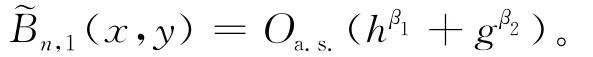
由文献［12］中引理3及分解（4）式得：

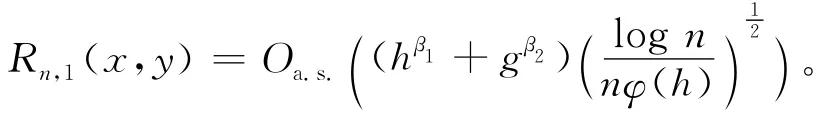
引理2 若假设（1）～假设（4）、（1）式成立，并且对∀l＝1，…，j，∀p≥2，则对∀x∈F有：

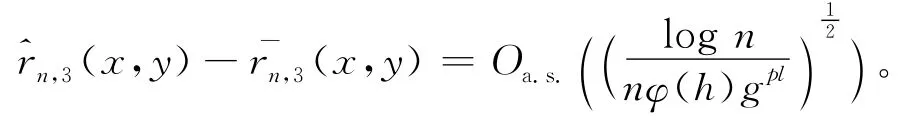
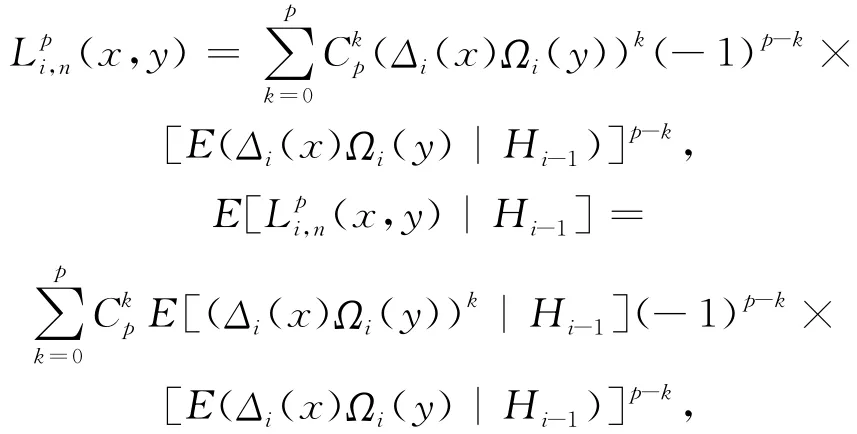
由Jensen不等式得：

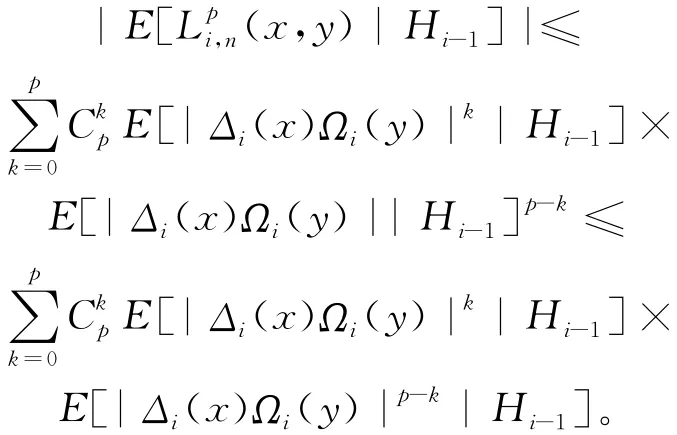
对∀m≥1，由假设（3）得：

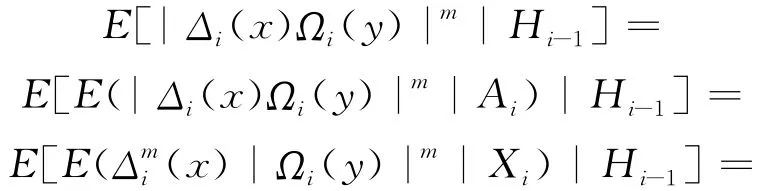
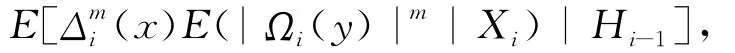
其中

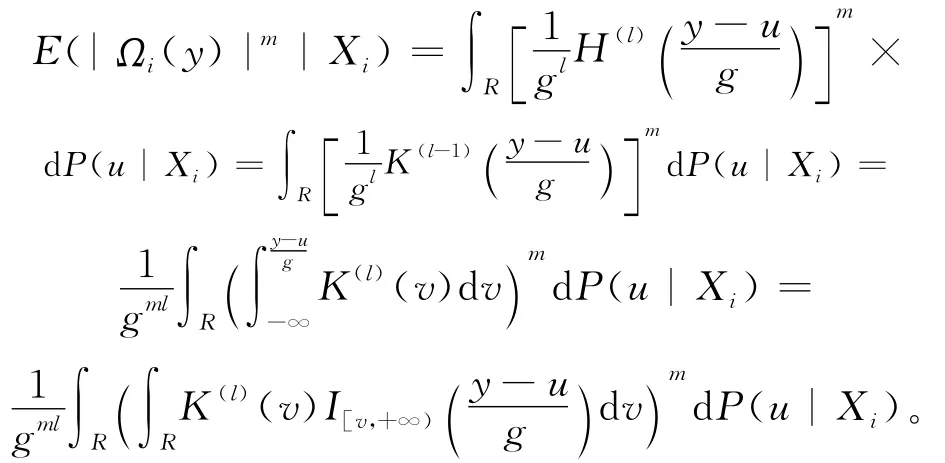
对于上述m，由Holder不等式得：

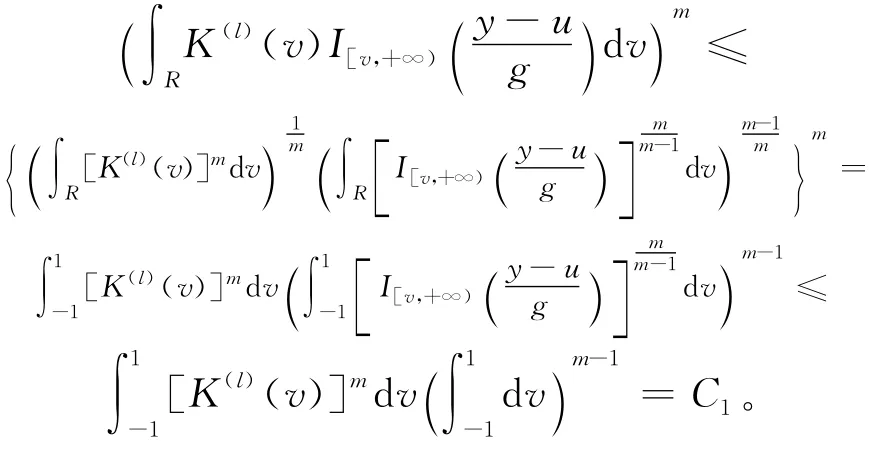
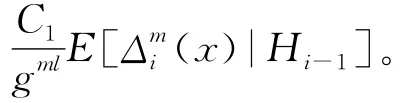
由文献［12］中引理2、假设（2）中的② 、③，且有核函数｜K｜≤a1，函数｜τ0｜≤c0，a1、c0、c1、c2为正实数，可以得到：

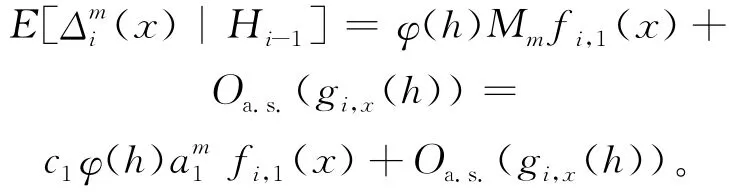
故

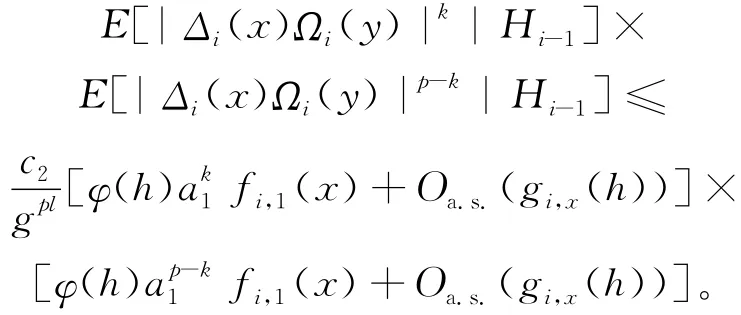
当n足够大时，有

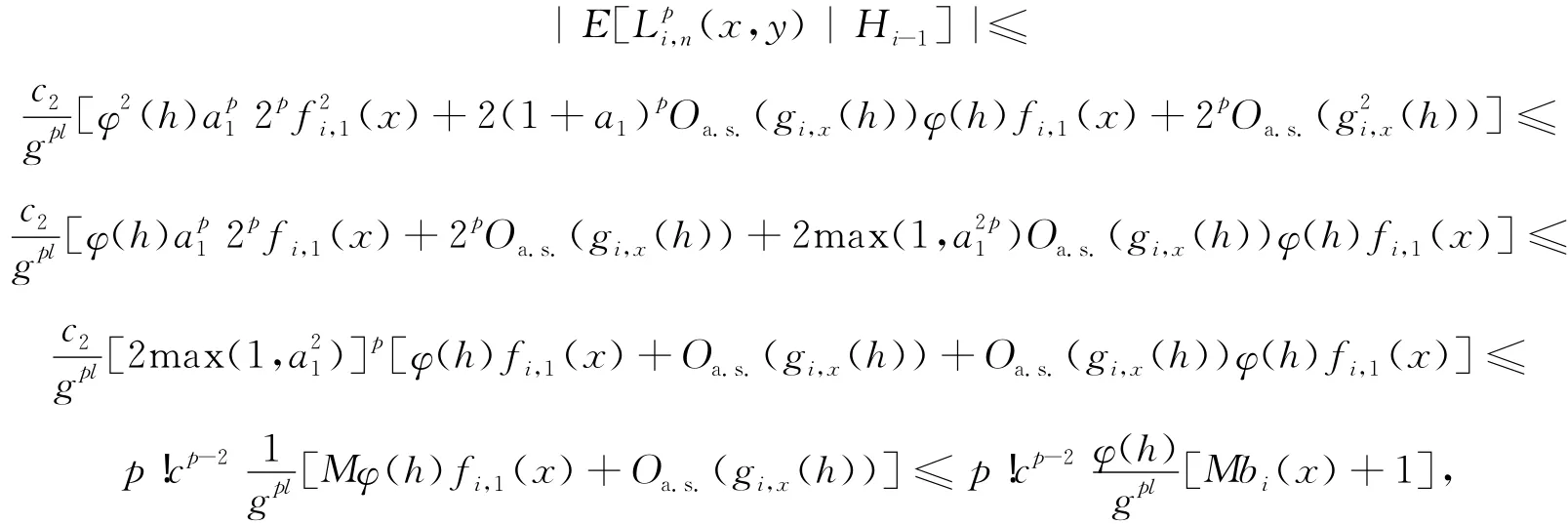
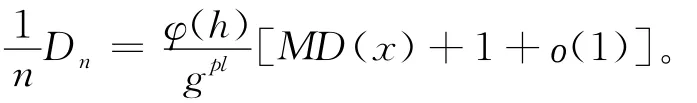
根据文献［12］中引理1，对∀ε0＞0，有

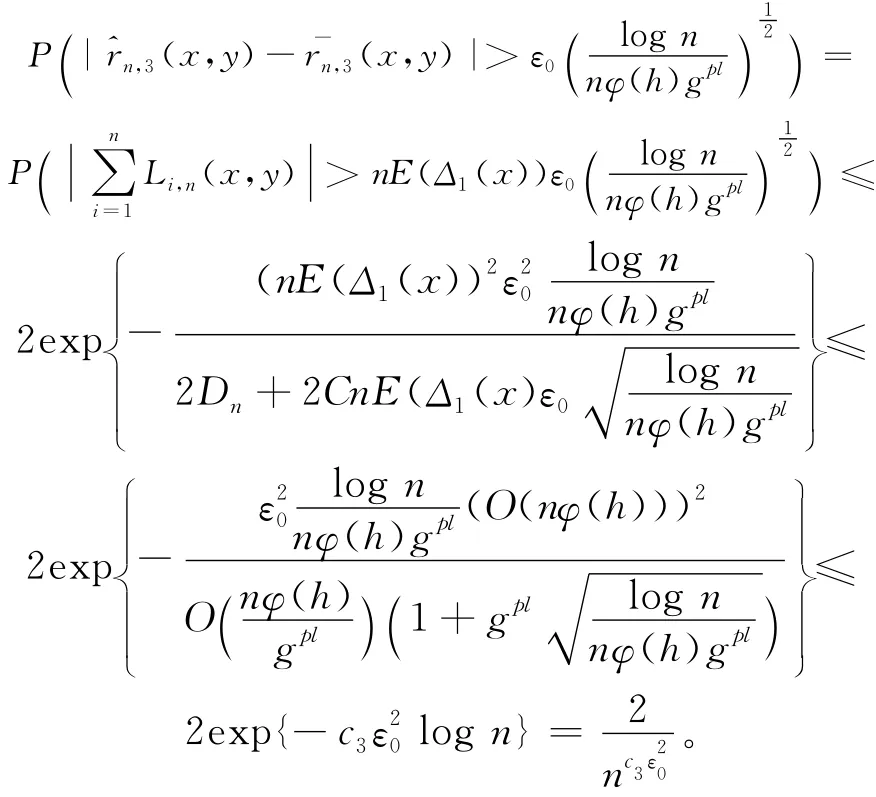
其中，c3为正常数。当ε0足够大时，可以得到：

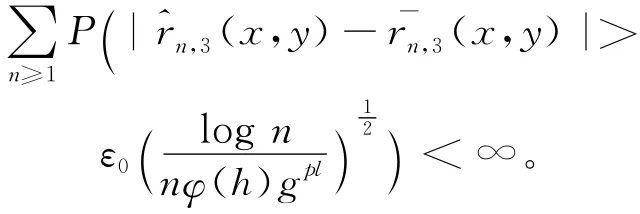
故引理得证。

引理3 若假设（1）～假设（4）、（1）式成立，对∀x∈F有：

证明

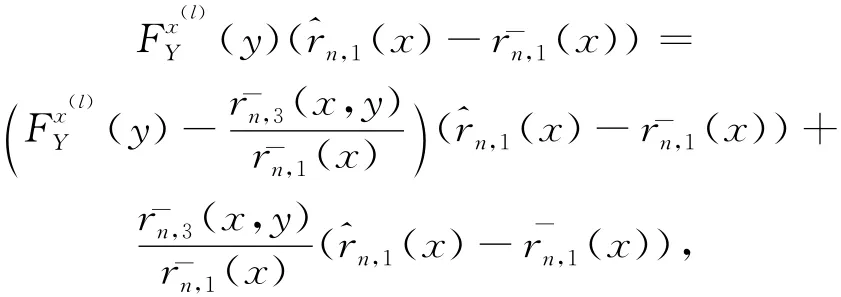
根据引理2得：

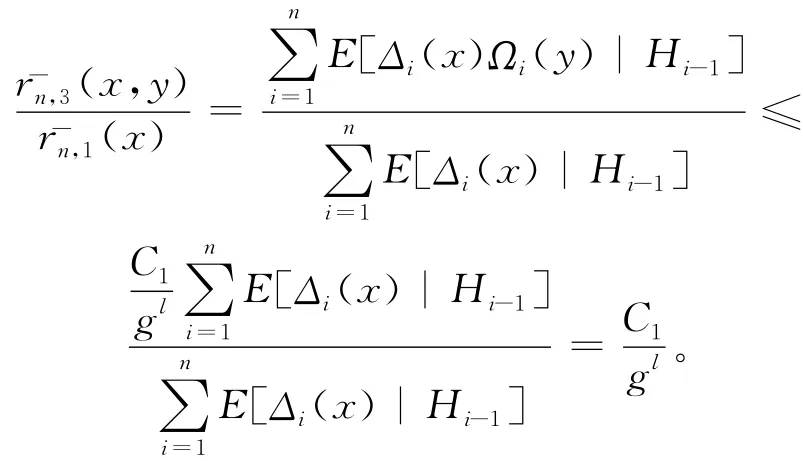
由分解（2）式，引理得证。

引理4 若假设（1）～ 假设（5）成立，则有：

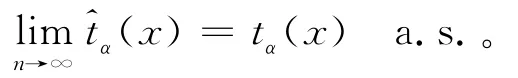
证明 易知（y）连续且严格递增，因此（y）存在且连续。

则对∀ε＞0，∃δ（ε）＞0，对∀y有：

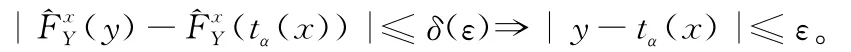
令y＝（x）有：

对∀ε＞0，∃δ（ε）＞0有：

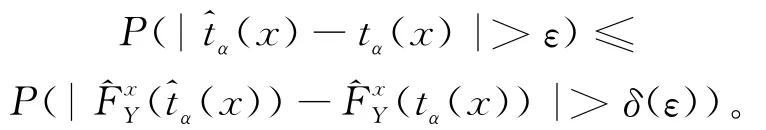
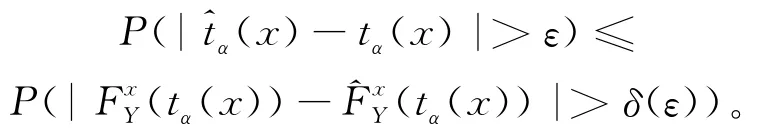
则引理得证。

综合文献［12］中引理1、引理3、本文引理3和（5）式即可证明定理1；综合本文引理4、文献［4］中内容即可证明定理2。

［1］ Samanta M.Non－parametric estimation of conditional quantiles［J］.Statist Probab Lett，1989，7：407－412.

［2］ Stute W.Conditional empirical processes［J］.Ann Statist，1986，14：638－647.

［3］ Gannoun A，Saracco J，Yu K.Nonparametric prediction by conditional median and quantiles［J］.J Statist Plann Infer，2003，117：207－223.

［4］ Ferraty F，Vieu P.Nonparametric functional data analysis：theory and practice［M］.New York：Springer，2006：17－86.

［5］ Azzedine N，Laksaci A，Ould Said E.On the robust nonparametric regression estimation for functional regressor［J］.Statist Probab Lett，2008，78：3216－3221.

［6］ Ezzahrioui M，Ould Said E.Asymptotic normality of the kernel estimators of the conditional quantile in the normed space［J］.Far East J Theoret Statist，2008a，25：15－38.

［7］ Ezzahrioui M，Ould Said E.Asymptotic results of the kernel estimator of the conditional quantiles in the normed space underα－mixing hypothesis ［J］.Commum Statist Ther Meth，2008b，37：2735－2759.

［8］ Laksaci A，Lemdani M，Ould Said E.A generalizedL1－approach for a kernel estimator of conditional quantile with functional regressors：Consistency and asymptotic normality［J］.Statist Probab Lett，2009，79：1065－1073.

［9］ Dabo－Niang S，Laksaci A.Nonparametric quantile regression estimation for functional dependent data［J］.Commum Statist Ther Meth，2012，41：1254－1268.

［10］ 范剑青，姚琦伟.非线性时间序列：建模预报及应用［M］.陈 敏，译.北京：高等教育出版社，2005：19－45.

［11］ Laib N，Louani D.Nonparametric kernel regression estimation for functional stationary ergodic data：asymptotic properties ［J］.J Multivariate Anal，2010，101：2266－2281.

［12］ Laib N，Louani D.Strong consistency of the regression function estimator for functional stationary ergodic data［J］.J Statist Plann Inference，2011，141：359－372.

［13］ Gheriballah A，Laksaci A，Sekkal S.Nonparametric M－regression for functional ergodic data ［J］.Statist Probab Lett，2013，83：902－908.

［14］ 魏亮瑜，凌能祥，李成好.基于遍历函数型数据条件分位数估计的相合性［J］.合肥工业大学学报：自然科学版，2012，35（4）：557－562.