基于Pushover原理的钢框架静力弹塑性分析

汪金祥， 肖亚明， 刘 顺， 董文秀

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

在我国，钢框架结构体系由于构件自重轻、适合标准化制作安装、比钢筋混凝土结构轻巧美观等优点，近几年发展迅速［1］，然而国内对钢框架的抗震性能研究还处于起步阶段。Pushover分析作为一种静力弹塑性分析方法，可以对结构的抗震性能进行近似评估，以此来了解结构的弹塑性地震反应［2］。这种分析方法的优点是既可以对结构在多遇地震下的弹性设计进行复核，也可以确定在罕遇地震作用下结构的破坏机制，找出薄弱环节，并在设计施工中加以重视。通过Pushover分析，可以得出每个构件的内力以及构件之间的相互作用关系，从而检查结构在地震作用下是否能够实现“强柱弱梁”和“强剪弱弯”的受力模式。

1 静力弹塑性分析的基本原理

静力弹塑性分析方法，也称为Pushover分析法，是一种基于性能评估现有结构和设计新结构的方法。Pushover方法，是指对结构模型沿结构高度施加一种特定分布模式且逐渐增加的侧向力或侧向位移，直到结构模型的控制点达到目标位移或结构破坏为止。因为该方法在静力加载状态下对结构进行弹塑性分析，所以本质上还是一种静力分析方法。

1.1 建立基底剪力和位移曲线

对结构施加单调增加的侧向荷载，计算结构的基底剪力（V）－顶点位移ΔT曲线，如图1所示。

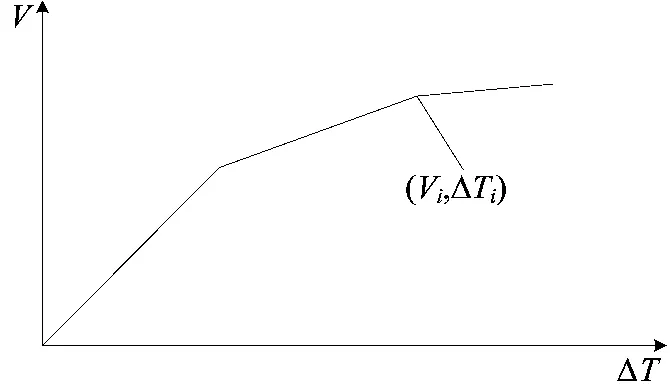
图1 基底剪力－顶点位移曲线

1.2 建立能力谱曲线

将基底剪力－顶点位移曲线转化为能力谱曲线［3］，如图2所示。

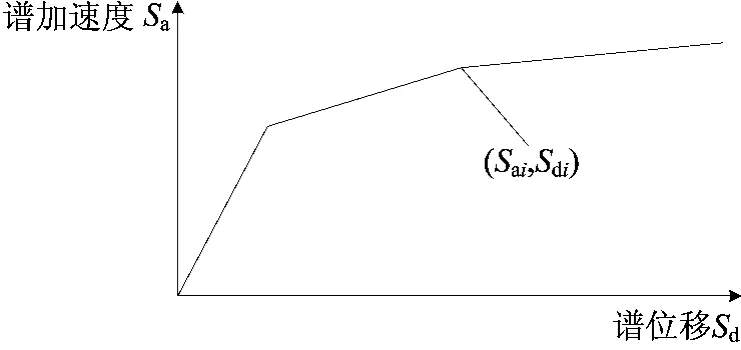
图2 能力谱曲线

需要根据（1）式逐点进行转换：

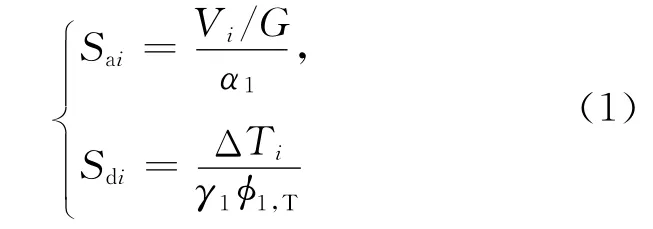
其中，（Vi，ΔTi）为基底剪力 －顶点位移曲线上的任一点；（）为能力谱曲线上相应的点；G 为总荷载效应代表值；γ1为第一振型参与系数为第一振型顶点振幅；α1为第一振型质量参与系数。

α1和γ1计算公式为：

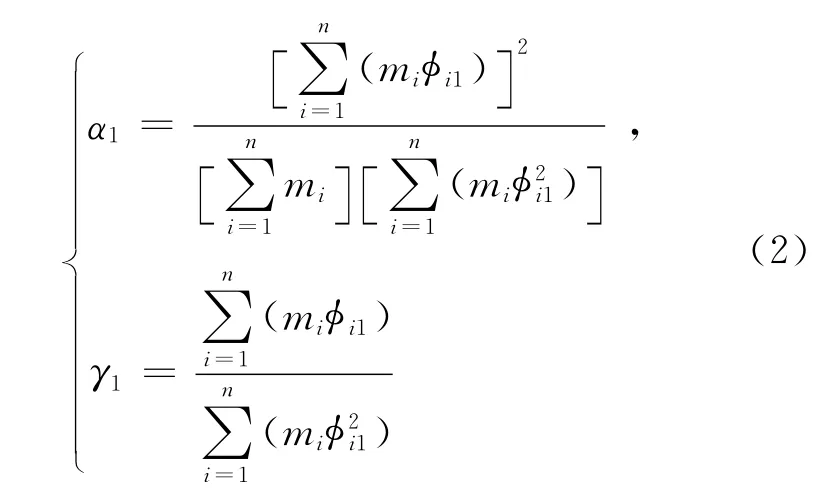
其中，n为层数；mi为i层质量为第一振型在第i层的振幅。

1.3 需求谱的转换

标准加速度反应谱如图3所示。在Ti周期处有如下关系：

由标准加速度反应谱（Sa－T）可转化为ADRS谱（Sa－Sd），即

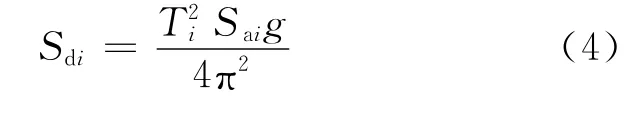
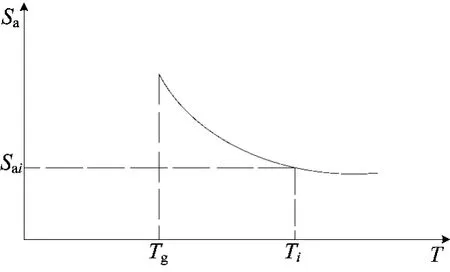
图3 标准加速度反应谱（Sa－T）

ADRS谱（Sa－Sd）即需求反应谱，如 图 4所示。

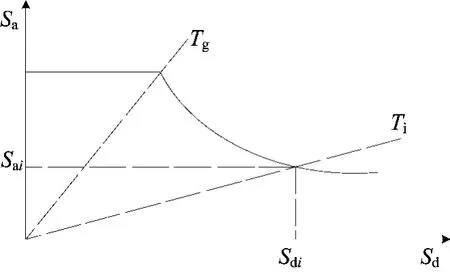
图4 ADRS谱（Sa－Sd）

在寻找地震需求与结构承载力供给之间的关系之前，应考虑结构的非线性耗能性质对地震需求的折减，如图5所示。

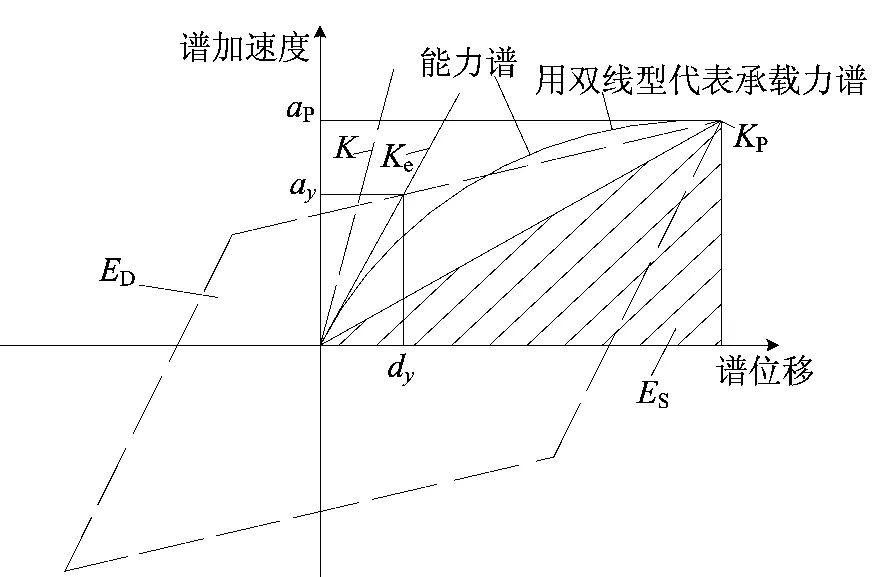
图5 反应谱折减用的阻尼转换

当结构在地震作用下处于非线性状态时，结构的固有黏滞阻尼和滞回阻尼会导致结构物在受力运动过程中产生耗能作用，这2种阻尼可用等效黏滞阻尼ζ［4］来评估：

其中，ED为单周期结构运动阻尼耗能，等于平行四边形的面积；ES为最大应变能，等于阴影斜线部分的三角形面积。

1.4 确定性能点

将能力谱和需求谱曲线置于同一ADRS图上，如图6所示。

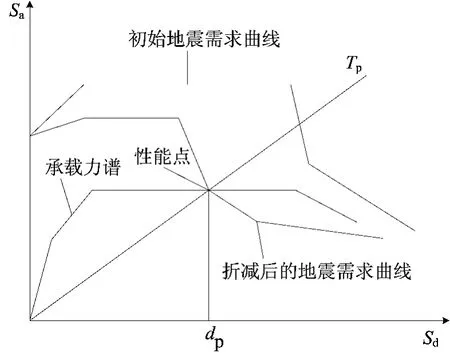
图6 能力谱与需求谱

两曲线的交点即为性能点，对应的位移即为在该地震作用下等效单自由度体系的谱位移。将谱位移按（1）式转化为结构的顶点位移，根据该位移在V－ΔT曲线上的位置，即可确定结构在地震作用下的塑性铰分布、侧移以及层间位移角等，以此来评估结构的抗震性能。如果两曲线没有交点，则表明结构抗震性能不足，需要重新设计。程序中所设定的反应谱与文献［5］中的地震反应谱表达式略有差异，需要进行等效转换，即

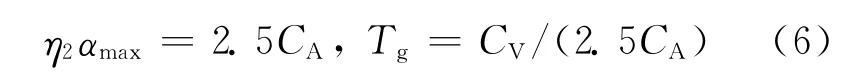
其中，Tg为特征周期；η2为阻尼调整系数。

2 计算步骤

2.1 建立结构模型并进行内力分析

先建立结构模型，然后根据设计规范，利用SAP2000结构分析软件施加相关荷载并进行各种荷载工况下的内力分析，查看应力比、挠度等是否符合要求。建模时，梁柱采用框架单元，钢筋混凝土组合楼板采用壳单元。

2.2 塑性铰的定义与设置

SAP2000目前在框架单元中提供了4种塑性铰：弯矩铰（M）、剪力铰（V）、轴力铰（P）和压弯铰（PMM）。软件允许在结构的同一位置定义不止1种类型的铰。在SAP2000中有3种类型的铰属性：默认的铰属性、用户指定的铰属性和生成的铰属性，而只有前2种可以被指定给框架单元［6］。由于结构的屈服位置一般发生在弹性阶段内力最大处，故推荐采用用户指定的方法为结构定义铰属性。对梁单元，一般仅考虑弯矩屈服所产生的塑性铰（M），对柱单元，一般考虑压弯作用所产生的塑性铰（PMM）。

2.3 侧向加载模式

侧向荷载的加载方式，既应当体现结构各楼层惯性力的分布特征，也应当使所求的位移尽可能真实反映结构在地震作用下的位移情况。

当结构在强震作用下进入弹塑性阶段后，其自振周期和惯性力分布随之改变，所以惯性力不能只用1种方式来反映，应当至少使用2种以上的侧向加载方式进行Pushover分析。在SAP2000中提供了3种Pushover分析工况：自定义、均匀加速度和振型荷载。其中均匀加速度方法相当于侧向均匀分布加载模式；振型荷载方法相当于侧向倒三角加载模式。在定义Pushover分析工况时，首先应当定义结构在自重作用下的内力与变形，因为其他工况的计算都是在此基础上进行的。结构的位移随着定义分析工况值的不断增加而增加，直至达到规定的位移。常用的Pushover分析工况有：① 重力＋振型1（纵向）；② 重力＋振型2（横向）；③ 重力＋x向加速度；④ 重力＋y向加速度。

2.4 结构分析与性能评价

经过Pushover分析以后，利用所得到的性能点以及性能点对应的变形，通过3个方面对结构的抗震性能进行评估［7］。

（1）顶点位移。观察结构的弹塑性顶点位移是否满足抗震规范要求。

（2）层间位移角。观察结构的弹塑性层间位移角是否满足抗震规范要求。

（3）构件局部变形。观察梁柱等构件的塑性铰变形是否超过了某一性能水准下的变形要求。

3 计算实例

3.1 工程概况

某一民用6层钢框架结构如图7所示。

结构层高均为3m，长边（x方向）为5跨（6m×5），短边（y方向）为3跨（6m＋3m＋6m）。钢材强度等级取Q345，梁截面尺寸为350×175×7×11，柱截面尺寸为400×300×10×16，支撑截面为φ100×10，楼板为120mm厚组合楼板，墙体维护结构外围等效取为6kN／m施加在框架上，内部分隔墙体等效取为3kN／m施加在框架上，按照荷载规范，考虑面层和吊顶重量，对组 合 楼 板 恒 载 取 为 5.0kN／m2，活 载 取 为2.0kN／m2。

本工程按8度（0.2g）抗震设防，场地类别为3类，设计地震分组为第1组，场地的特征周期为0.45s。

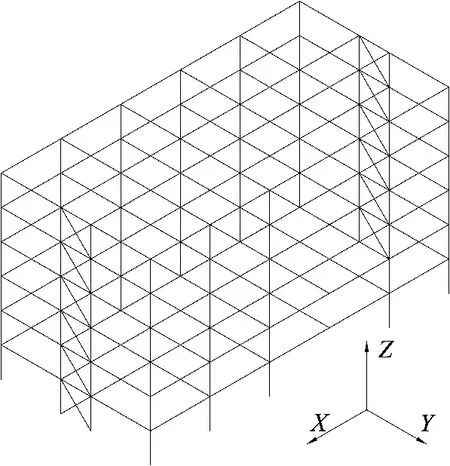
图7 结构三维模型图

经过SAP2000的荷载工况组合分析，可得出钢梁的最大应力比为0.924，钢柱的最大应力比为0.790，钢梁的最大挠度为8.9mm，强度和挠度均在允许范围内［5］。

结构的模态周期与频率见表1所列。

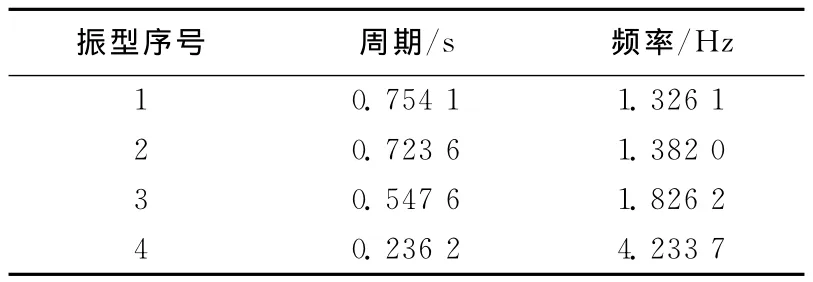
表1 模态周期与频率

由表1可以求出结构第一扭转振型（振型3）和第一平动振型（振型1）周期之比小于0.9，满足规范对结构平面布置的要求。

结构受到多遇地震作用下的侧移和层间位移角见表2所列。

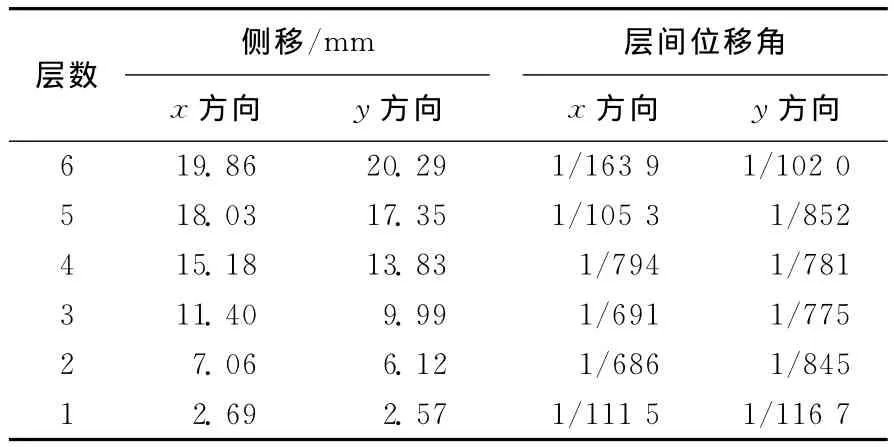
表2 多遇地震作用下的侧移和层间位移角

由表2中可知结构在多遇地震下层间位移角均满足规范所规定的的限值（1／250）［8］。

3.2 侧向加载模式

对本算例，在进行Pushover分析侧向加载时，设置了4种加载模式：① 重力＋Mode 1（x向）；② 重力＋Mode 2（y向）；③ 重力＋Accel（UX）；④ 重力＋Accel（UY）。

3.3 Pushover计算结果与分析

3.3.1 参数确定

3.3.2 结构底部剪力－顶点位移

由求得的性能点可知，结构在加载模式①作用下，底部最大承载力为4 127.23kN，顶点位移为168.13mm；在加载模式②作用下，底部最大承载力为4 051.09kN，顶点位移为115.87mm；在加载模式③作用下，底部最大承载力为4 679.80kN，顶点位移为161.32cm；在加载模式④作用下，底部最大承载力为4 842.24kN，顶点位移为98.94mm。4种加载模式中顶点位移最大值＝168.13mm＜18 000mm×2%＝360mm（2%是抗震规范规定的弹塑性层间位移角限值），所以顶点位移满足弹塑性极限要求。

从所得数据可知，对于x向加载或y向加载，振型加载模式比加速度加载模式的顶点位移大，但是后者的底部最大承载力却优于前者。这说明不同的加载模式会对结构的受力分析结果产生影响。

3.3.3 结构层间位移角

根据文献［9］可知，对于低层钢框架结构，采用振型加载可以较为准确地反应结构地震作用时的层间位移角。结构在罕遇地震作用下的层间位移角见表3所列。

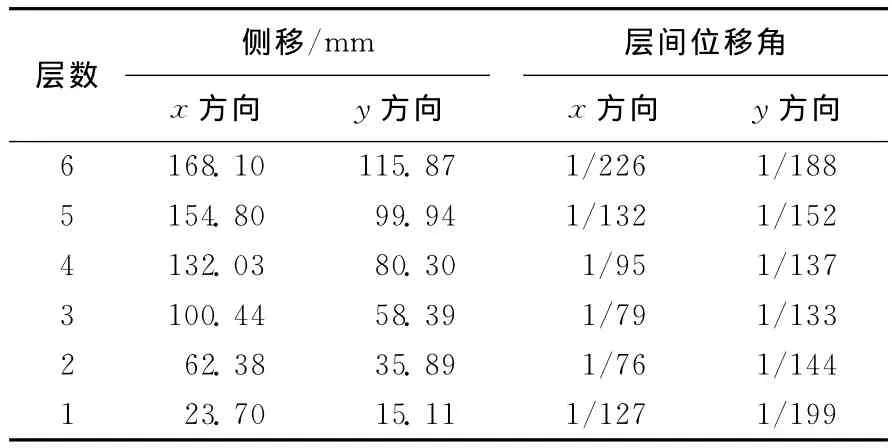
表3 罕遇地震作用下的侧移和层间位移角

由表3可知，在罕遇地震作用下，结构的最大层间位移角小于抗震规范规定的弹塑性层间位移角限值（1／50），但在x方向上结构中部的层间位移角接近限值，属于薄弱部位，设计时应当予以重视。

3.3.4 结构塑性铰分布

不同加载模式下结构的塑性铰分布如图8所示。

由图8可知，结构在弹塑性阶段，在加载模式①和加载模式③作用下，塑性铰首先出现在2层边跨梁端；在加载模式②和加载模式④作用下，塑性铰首先出现在中部底层柱端，这是由于在横向跨中布置支撑，使得结构在该处刚度增大，当受到地震作用时该部位承担了较大的作用力，从而先于其他部位产生塑性铰。从最后的塑性铰分布可以看出，塑性铰大多数出现在框架梁端，基本符合“强柱弱梁”的设计要求。对同一方向上作用不同的加载模式，也会对结构的最终塑性铰分布产生影响。

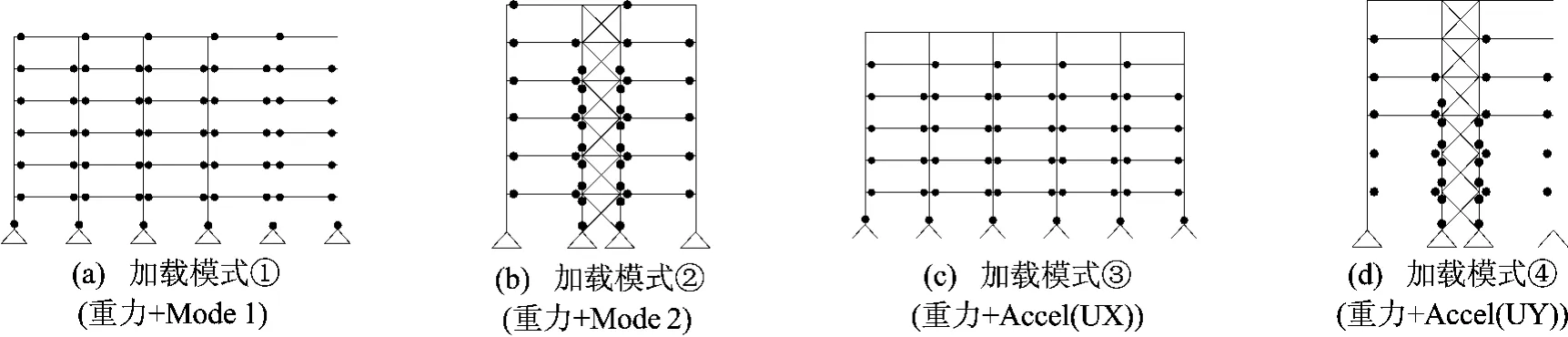
图8 不同加载模式下结构塑性铰分布

从上述分析可知，该工程实例满足设计要求，而且从计算结果中可以观察出构件局部是否满足塑性限值要求，从而根据抗震需要考虑对结构进行局部加强。

4 结 论

本文根据Pushover分析原理，结合抗震设计规范对1个6层钢框架结构进行了静力弹塑性分析，结果表明：

（1）Pushover分析过程中，应当注意加载模式的定义和选取，不同的加载模式会对结构的受力分析结果产生影响。

（2）Pushover分析可以得出罕遇地震下的基底剪力－顶点位移曲线、层间位移角和塑性铰的分布，从而可以较为全面地反映结构在强震作用下的实际发展过程。

（3）相对于时程分析，Pushover分析概念更为清晰，实际操作也较为简单，可以使设计人员在了解原理的基础上对结构进行强震下的抗震分析，并对薄弱环节进行设计优化。

［1］王元清，石永久，陈 宏，等.现代轻钢结构建筑及其在我国的应用［J］.建筑结构学报，2002，23（1）：2－8.

［2］叶献国，种 迅，李康宁，等.Pushover方法与循环往复加载分析的研究［J］.合肥工业大学学报：自然科学版，2001，24（6）：1019－1024.

［3］黄 鑫.Push－over分析的研究及应用［D］.青岛：青岛理工大学，2007.

［4］王大绥，贺军利，张凤新.静力弹塑性分析（Pushover Analysis）的基本原理和计算实例［J］.世界地震工程，2004，20（1）：45－53.

［5］GB 50011－2010，建筑抗震设计规范［S］.

［6］北京金土木软件技术有限公司，中国建筑标准设计研究院.SAP2000中文版使用指南［M］.第2版.北京：人民交通出版社，2012：466－476.

［7］黄 鑫，刘 瑛，黄 河.基于Push－over原理的SAP2000结构弹塑性分析实例［J］.青岛理工大学学报，2007，28（4）：19－23.

［8］GB 50017－2003，钢结构设计规范［S］.

［9］毛建猛.Pushover分析方法的改进研究［D］.哈尔滨：中国地震局工程力学研究所，2008.