Crack3D和ANSYS求解裂纹柱体的圣维南扭转问题

汤昕燕， 丁兰英

（南京农业大学 工学院，江苏 南京 210031）

本文结合专业程序Crack3D［1］及通用软件ANSYS，得到了一种新的计算带裂纹柱体的圣维南扭转问题的有限元方法，使用该方法对带裂纹柱体的圣维南扭转问题算例进行了计算，得到了应力强度因子、扭转刚度D 和剪应力、等数值结果。

从数值结果看，该方法功能强大，可应用于带裂纹柱体圣维南扭转问题的求解。

1 圣维南扭转问题

如图1所示，Ωb为柱体的任意横截面，Γ为Ω的边界，x、y、z为截面的惯性主轴。这里没有显示oz轴，坐标原点o设置在下端横截面Ωb的形心c处，扭转力偶矩Mk作用于顶部截面Ωt上。

设柱体的长度为L，根据文献［2］关于圣维南扭转问题的理论，在直角坐标系（x，y，z）中，由于扭转力偶矩Mk的作用，柱体的位移分量为：

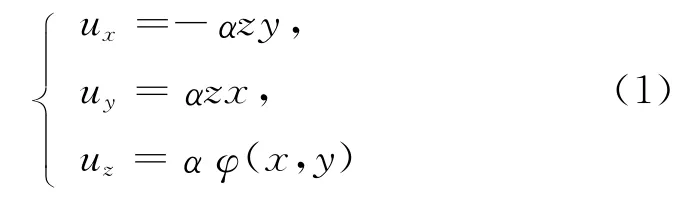
其中，α为柱体单位长度的扭转角，即扭率，可以由2个不同截面之间的相对扭转角确定。

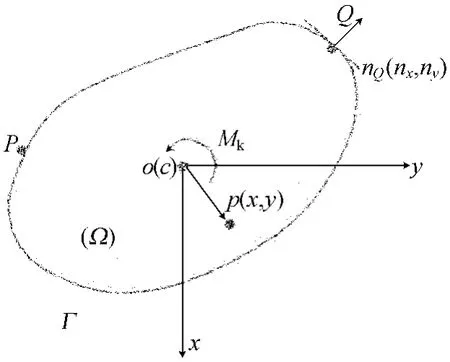
图1 扭转柱体的一般横截面

设φ（x，y）为区域Ω上的一个平面调和函数，则扭转刚度D为：

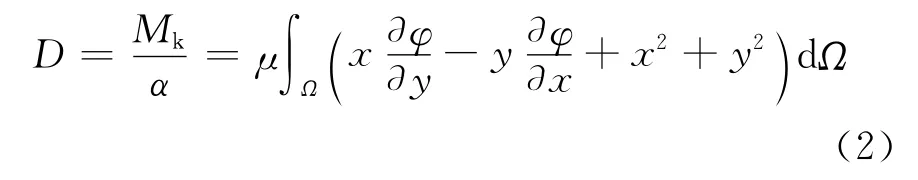
其中，μ为剪切弹性模量，μ＝E／2（1＋ν）。

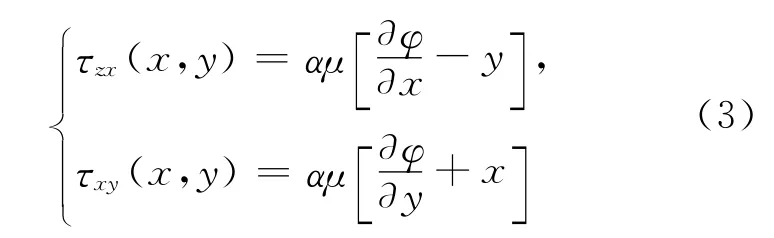
2 有限元法求解圣维南扭转问题

对任一截面取正方形截面，边长a为20mm的柱体，顶部截面Ωt与底部截面Ωb之间的距离l为30mm，弹性模量E为100GPa，泊松比ν为0.3，初应力σy为100GPa。该柱体带有一个边裂纹，裂纹通过柱体轴线沿纵向贯穿，裂纹宽度为a／2。采用结合Crack3D和ANSYS的有限元方法求解该问题，具体步骤如下：

（1）通过ANSYS预处理器建立几何模型［3］。网格的几何模型使用8个节点块单元［4］，如图2所示，图中Ω为中间截面。

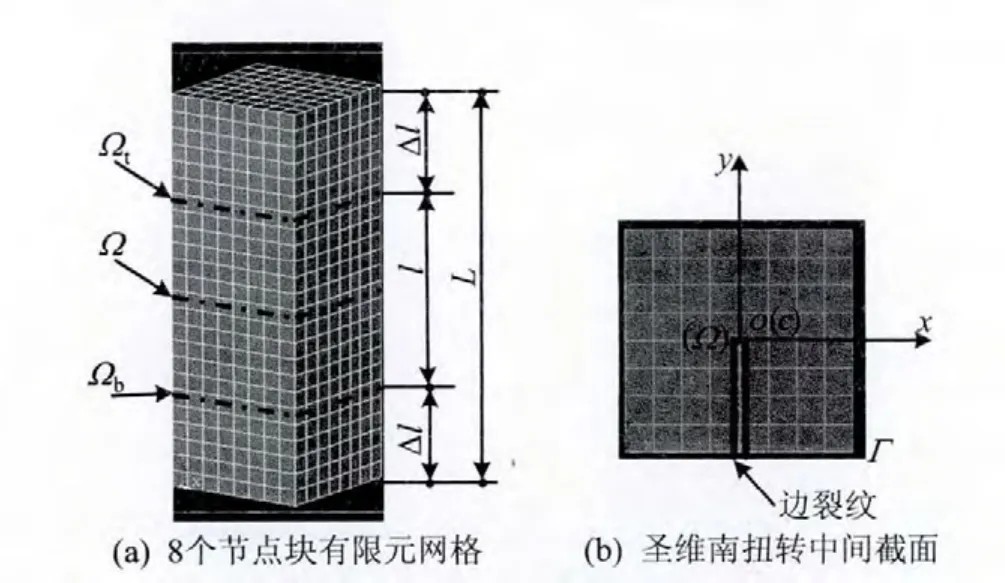
图2 正方形截面扭转柱体

（2）使用主菜单／预处理／创建／节点／写节点文件、主菜单／预处理／创建／单元／写单元文件的GUI操作［5］，获得Elems.dat和 Nodes.dat文件。

（3）将Elems.dat和 Nodes.dat文件输入到专业程序Crack3D中的预编码Mesh3D交互界面中，执行后可生成数据文件Crack3D.msh。

（4）运用 Elems.dat和 Nodes.dat文件，建立控制数据文件Crack3D.dat。

（5）将数据文件Crack3D.msh和Crack3D.dat输入到专业程序Crack3D中的主编码Crack3D交互界面中，执行后可获得Crack3D.ans和Crack3D.res的数据结果。

（6）将数据文件Crack3D.ans输入到专业程序Crack3D中的后编码Post3D交互界面中，执行后可将Crack3D格式的数据结果转换为ANSYS后处理器中的数据结果格式。

（7）在ANSYS后处理器中读取数据文件Crack3D.res，可得到位移、应变和应力数据。

（8）从Crack3D.res文件中，提取出Ωt和Ωb截面上的节点位移ux（或uy），并将其代入（4）式中，即可计算得到α值。

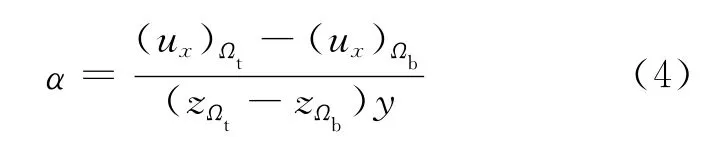
（9）从Crack3D.res文件中，提取出中间截面Ω边界Γ上的节点位移uz，并将其代入（5）式中，即可得到扭转刚度D值。

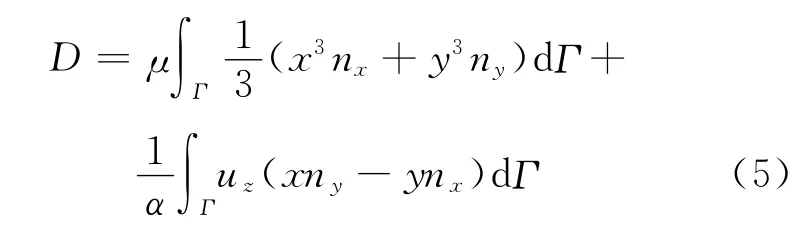
若将D转化为无量纲参数D／（μa4），则可与理论结果进行比较。

（10）从Crack3D.res文件中，提取出截面Ω边界Γ 上的最大剪应力τ（τ1、τ2），并将其转化为无量纲参数τ1／（αμa）、τ2／（αμa），可与理论值进行比较。

（11）从Crack3D.res文件中提取出节点的反作用力，并确定作用于顶端截面Ωt的扭矩Mk。通过截面Ω边界Γ上的最大剪应力（或τ2），计算出无量纲参数并与理论值进行比较。

（12）对于图2b中的截面Ω，从Crack3D.res文件中，提取出节点位移，则可计算出裂纹尖端的张开位移COD，代入（6）式中，即可得到裂纹尖端的应力强度因子［6］。

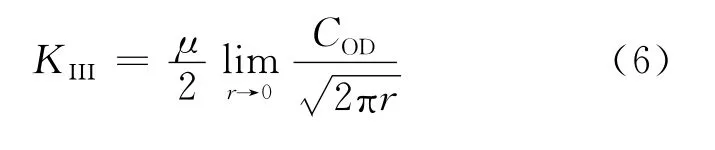
3 无裂纹的圣维南扭转问题数值验证

若不考虑带裂纹的情况，利用ANSYS软件将柱体自动划分为正方形网格，边长为2.5cm，根据Elems.dat和Nodes.dat文件，网格共包括1 536个单元和2 025个节点。

在中间截面Ω的边界Γ上，一些特殊节点的编号如图3所示。

将下端面上的节点（节点编号为6、14、22、29、57）在x、y轴方向固定，用以限制转动，但允许在z轴方向产生位移。

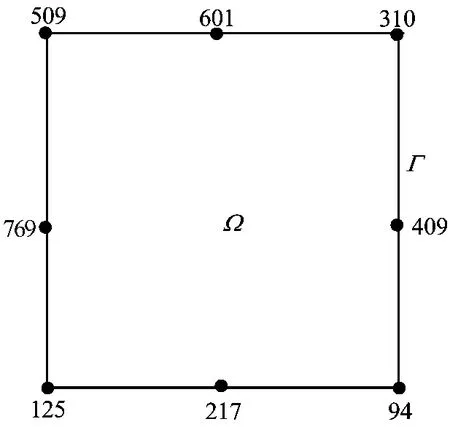
图3 无裂纹柱体中间截面Ω的边界Γ上特殊节点

上端面在4个节点（节点编号为110、325、494、685）上施加位移载荷，ux＝0.02mm，uy＝－0.02mm，ux＝－0.02mm，uy＝－0.02mm。

使用上述方法求解，将节点位移ux、uz；剪应力、；反 力 Fx、Fy及 参 数α、D／（μa4）、τ／（αμa）、Mk／（τa3）的数值结果与理论值比较［7］，结果见表1、表2所列。

表1 Crack3D编码计算参数值结果与理论值比较

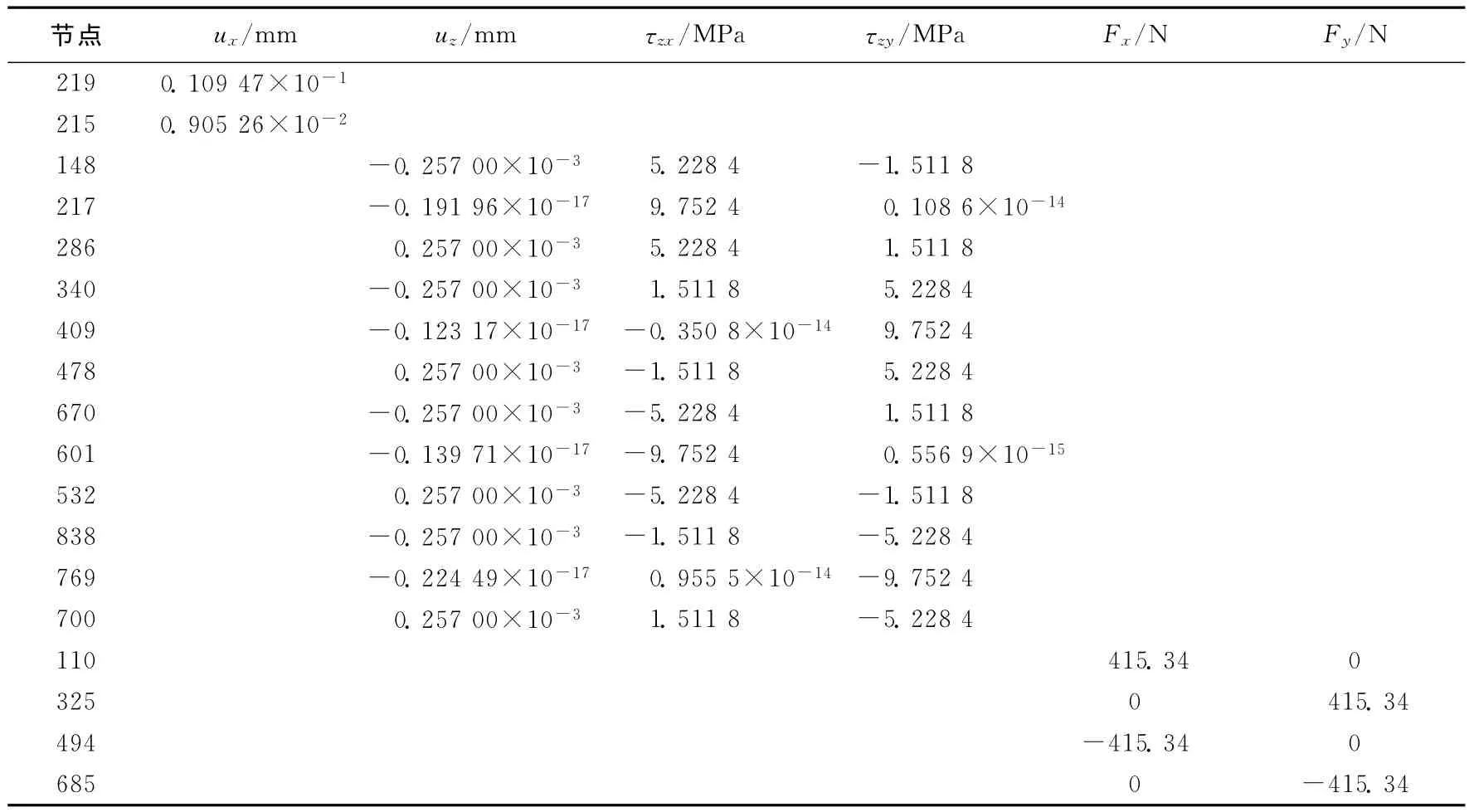
表2 Crack3D编码计算得到的部分节点数值结果

由表1、表2可以看出，新的有限元方法计算得到的数值结果与理论结果吻合较好，说明此方法求解扭转问题是成功的。

4 新方法计算带裂纹的圣维南扭转问题

对于存在裂纹的情况，采用新的有限元方法计算应力强度因子。在该种情况下，中间截面Ω的边界Γ上特殊节点编号如图4所示。

将下端面上的节点（节点编号为627、1 626、1 126、6、1、2）在x、y轴方向固定，用以限制转动，但允许在z轴方向产生位移。

上端面在5个节点（编号为646、1 670、1 146、146、50）上施加位移载荷，分别如下：ux＝0.02mm，ux＝0.02mm，uy＝0.02mm，ux＝－0.02mm，uy＝－0.02mm。

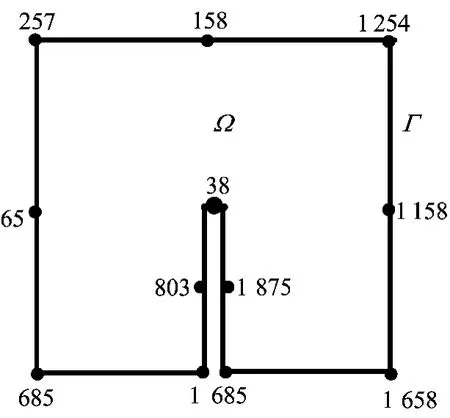
图4 带裂纹柱体中间截面Ω的边界Γ上的特殊节点

使用上述方法求解该扭转裂纹问题，ux、uz、、Fx、Fy数值结果见表3所列。

表3 使用新方法时Crack3D编码计算得到的部分节点数值结果

经 计 算，α 为 2.452 3×10－5（°）／mm，D／（μa4）为1.105 1，τ／（αμa）为1.078 3，Mk／（τa3）为1.184 9为11.678 0N／mm3／2。据此可知带裂纹柱体扭转总位移变形情况，如图5所示。

图5 裂纹柱体扭转总位移变形

5 结束语

本文采用结合Crack3D和ANSYS的有限元方法求解圣维南扭转问题是成功的，可应用于实际计算中。同时，若将计算所得的裂纹柱体扭转刚度和无裂纹柱体扭转刚度数值结果取比值，即η＝Dw／＝0.508 3。其中，Dw为带裂纹柱体扭转刚度，为无裂纹柱体扭转刚度。由比值可以看出，带裂纹柱体的扭转刚度几乎是无裂纹柱体扭转刚度的1／2，说明带裂纹柱体扭转刚度下降剧烈。

［1］Zuo Jianzheng，Deng Xiaomin，Sutton MA.User＇s manual and verifications in CRACK3Dversion 4.50［Z］.University of South Carolina，2007.

［2］Muskhelishvili N I.Some basic problems of the mathematical theory of elasticity［M］.Groningen，Netherlands：P Noordhoff，1953：424－429.

［3］胡于进，王璋奇.有限元分析及应用［M］.北京：清华大学出版社，2009：79－83.

［4］张洪信.有限元基础理论与ANSYS应用［M］.北京：机械工业出版社，2008：158－163.

［5］张乐乐.ANSYS应用教程［M］.北京：清华大学出版社，2006：43－47.

［6］孙训芳.断裂力学教材［M］.北京：高等教育出版社，1980：63－67.

［7］钱伟长.弹性柱体的扭转理论［M］.北京：科学出版社，1956：89－95.

［8］孙 欣.三维应力约束及厚度效应的有限元分析［J］.合肥工业大学学报：自然科学版，2008，31（7）：1101－1104.