抗磁性的经典模型与计算

谢莉莎， 吴本科， 刘彩霞， 邓小玖

（合肥工业大学 电子科学与应用物理学院，安徽 合肥 230009）

物质的抗磁性本质上是一种量子现象，严格意义上经典理论不能诠释这一现象，只能给出定性、半定量的解释。物质抗磁性经典解释的核心问题是如何解释轨道电子在外磁场中所产生的附加磁矩。

目前关于物质抗磁性的解释主要有电子轨道磁矩的进动理论、感生电场理论以及洛仑兹力的作用等。文献［1］以原子位于轴对称时变磁场的中心为例，描述了原子核外电子在感生电场作用下速度的变化，并计算了电子轨道磁矩的增量（附加磁矩）。然而这个特例不能真实描述外磁场的建立以及物质中原子的位置状态［2］，需要一个一般性的描述才更为合理。文献［3－4］考虑到核外电子受到磁场洛仑兹力的作用，在核外电子轨道不变的前提下，电子运动的速率必然改变，从而解释电子轨道运动的附加磁矩。然而洛仑兹力的作用不能改变电子的运动速率，因而这种描述不能解释电子运动速率改变的原因。电子轨道磁矩的进动理论指出，电子轨道磁矩绕磁场的进动将产生一个等效的附加磁矩［5－6］。实际上电子轨道磁矩绕磁场进动时，磁矩的大小及其沿磁场方向的分量是不变的［7］。

本文基于感生电场、电子轨道磁矩的进动以及洛仑兹力的共同作用，自洽而普遍性地解释了物质的抗磁性，得出抗磁性物质中轨道电子产生的附加磁矩为并得到与量子力学理论一致的结论。

1 抗磁性的普遍性解释

设抗磁性物质中的外磁场经时间t由0增加到B，方向沿z轴的正方向。由于磁场的变化，将在抗磁性物质中激发感生电场E。设电子沿半径为r的轨道运行1周的时间为δt＝T＝2πr／v，其动能的增量为：

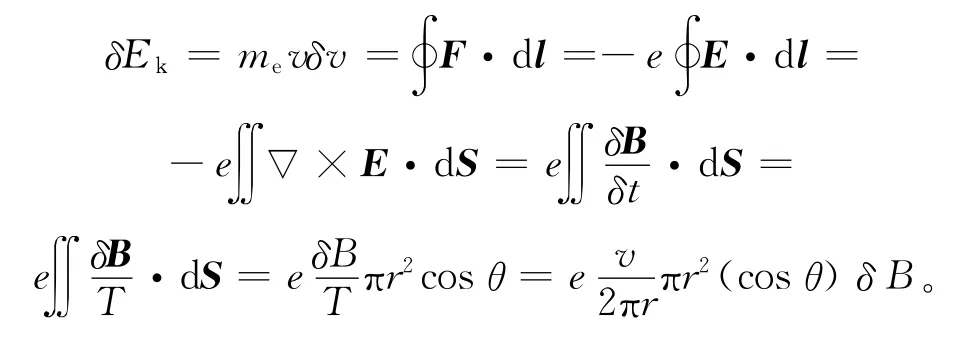
则有：

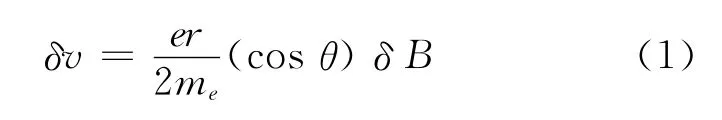
运算中认为在原子范围内磁场为均匀时变场，θ为电子轨道角动量L与磁场B的夹角。由（1）式可知，当外磁场取值为B时，电子的速率为

一般Δv≪v0。电子轨道角动量的增量为：

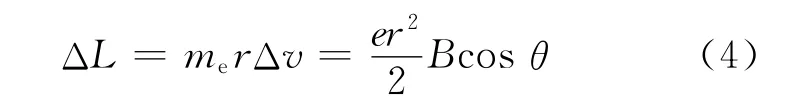
cosθ≤90°时，电子轨道角动量的值是增大的，ΔL的方向与L相同；cosθ＞90°时，电子轨道角动量的值是减小的，ΔL的方向与L相反。电子轨道磁矩μm与轨道角动量L 的关系为［7－8］：

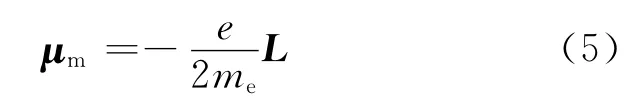
由（5）式可知，由于电子轨道运动角动量的变化ΔL，其轨道运动的附加磁矩为：

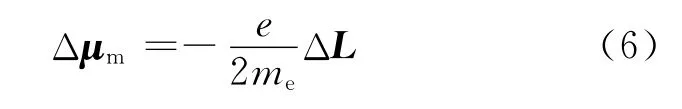
则电子的总磁矩为：

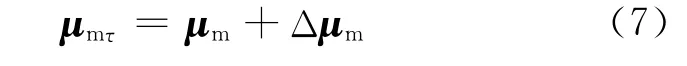
对于抗磁性物质，原子（或分子）的固有磁矩为0，则在外磁场中，具有Z个电子的原子总磁矩为

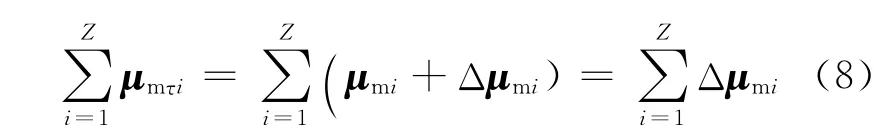
显然（8）式还不能解释物质的抗磁性，也就是说仅有感生电场的概念并不能解释物质的抗磁性。由于电子磁矩在外磁场B中还要受到磁力矩M作用，即

则电子的轨道角动量J＝L＋ΔL在磁力矩M的作用下绕B 方向（z轴的正方向）产生拉莫尔进动，即

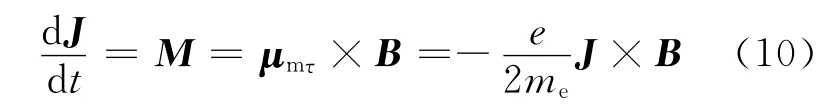
（10）式也可表示为：

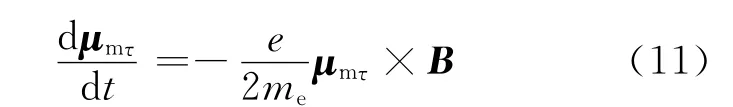
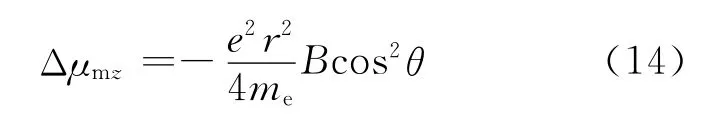
令ρ＝rcosθ，由于抗磁性物质的原子总角动量为0，原子的核外电子球对称分布，因而（14）式可进一步表示为：

抗磁性物质的原子总磁矩为所有轨道电子附加磁矩Δμmz的和，即

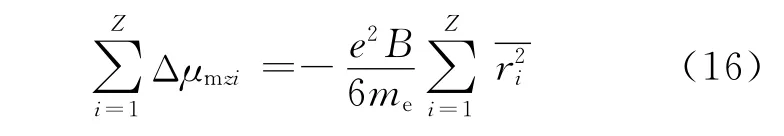
（16）式反映了抗磁性物质在外磁场中的抗磁性，与量子理论的结论一致［9－10］。

2 电子运动轨道的稳定性

在平面极坐标下，磁场中原子核外电子轨道运动的径向方程可表示为：

（18）式表明电子的运动轨道是稳定的，即电子的轨道半径近似保持不变。反之，若在（17）式中令¨r＝0，即假设电子的轨道不变，可求得（3）式。

3 结 论

本文分析了任意取向的电子轨道磁矩在磁场中任意一点产生的抗磁效应，指出自洽地解释物质的抗磁性必须同时考虑电子轨道磁矩的进动、感生电场以及洛仑兹力的作用。本文的分析表明：感生电场的作用是电子轨道运动产生附加磁矩的根本原因；由（17）、（18）式可知，在库仑力和洛仑兹力的共同作用下电子的运动轨道是稳定的；由于电子轨道磁矩的拉莫尔进动，使得附加磁矩的时间平均值为磁场的负方向，确定了物质的抗磁性。物质抗磁性的经典解释对相关应用研究具有一定的参考价值。

［1］费曼 R P，莱登 R B，桑兹 M.费曼物理学讲义：第2卷［M］.王子辅，译.上海：上海科学技术出版社，1981：427－428.

［2］秦光戎.关于抗磁性的感生场解释［J］.北京师范大学学报，1982（2）：69－74.

［3］哈里德D，瑞斯尼克R.物理学：第2卷、第1册 ［M］.郑永令，等，译.第2版.北京：科学出版社，1981：374－375.

［4］赵凯华，陈熙谋.电磁学：下册［M］.北京：人民教育出版社，1978：117－119.

［5］程守洙，江之永.普通物理学：第2册［M］.第5版.北京：高等教育出版社，1998：283－284.

［6］张三慧.电磁学［M］.第2版.北京：清华大学出版社，1999：290－292.

［7］周衍柏.理论力学教程［M］.北京：人民教育出版社，1979：213－215.

［8］陈宏芳.原子物理学［M］.北京：科学出版社，2006：96－97.

［9］福里格S.实用量子力学：上册［M］.宋孝同，高 琴，梁仙翠，等，译.北京：高等教育出版社，1983.：338－341.

［10］戴道生，钱昆明.铁磁学：上册［M］.北京：科学出版社，1987：33－36.