电容法的工业酒精浓度测量及其非线性修正＊

雷志勇，王 娇，王泽民

（西安工业大学 电子信息工程学院，710021）

工业酒精、也称变性酒精、工业火酒．工业酒精用途广泛，是基础的有机化工原料和优质燃料，广泛用于印刷、电子、五金、香料、化工合成、医药合成等方面，不同的应用场合对于酒精浓度的要求各不相同，另一方面，生产加工中对酒精的浓度值的精确度要求很高，微小的浓度差对结果有着很大的影响［1］．目前，酒精浓度测量主要有短波法、密度法和电容法，因为电容法设备简单，价格低廉，所以，得到广泛应用．

由于测量环境的影响，以及电容器的边缘效应，分布电容，电子元器件的漂移等都会造成测量误差，这往往使输出呈非线性［2］．针对上述情况，国内外学者从电容式传感器的测量电路以及数据处理等方面进行了相应改进，取得了一定的成果，学者王兆华设计了有源电桥式电路［3］，实现了电容传感器线性输出，在一定程度上解决了非线性问题，但是受环境影响较大，精度低；学者李杏华等人在测量电路中增加了平衡电路［4］，用于补偿电子元器件特性漂移带来的测量误差，该方法误差小，但精度相对有限；樊尚春等学者采用分段线性化对传感器输出数据处理［5］，该方法局限性较大．本文在国内外研究成果上，提出了利用最小二乘法对电容传感器的输出进行非线性处理的方法，来消除非线性参量对测量结果的影响，并结合计算机在线数据处理，完成非线性修正，最小二乘法的优点是采用以梯度为准则的寻优策略，简单方便且误差较小．本文最后进行了实验验证，实验结果表明，该方法能有效提高测量精度，且处理灵活．

1 电容法测工业酒精浓度测量原理

由物理学知识可知，物体间电容量的大小取决于电容器极板的大小、极板间介质的介电常数、形状和相互位置．其关系可表示为c＝f（ε，d，s），其中c为电容板的电容量，d为板间距离，s为极板的相互覆盖面积，ε为极板间介质的介电常数．故可知当固定d和s不变时，极板的电容量伴随着板间介电常数的改变而发生变化．

如图1所示为圆形平板电容的结构，该电容的极板面积为s，板间距离为d．两平行板固定不动，当平行板电容器的两板间距d比极板面s小很多时，可忽略边缘效应，看成一个无穷大理想平行板电容器，本文所使用电容器的尺寸为：电容板半径r＝5cm，板间距离d＝0．5cm．

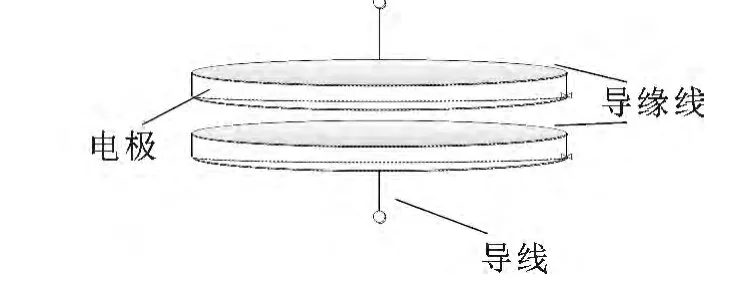
图1 平板电容结构Fig．1 Plate capacitor structure

若酒精与水的混合物充满整个电容器，设此时的混合物的等效介电常数为ε，则电容量为

设待测混合液中酒精的体积份额即体积浓度为Dv，εc和ε0分别为纯酒精和纯水时的介电常数，则当电容传感器浸入酒精和水的的混合液体中时，混合介电常数ε［6］可表示为

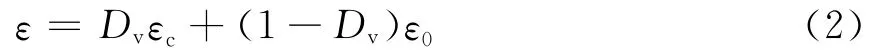
当电容传感器浸入纯水的溶液时电容值C0表示为

则当酒精的体积份额为Dv时，混合液体引起的电容传感器的总电容值为C，ΔC为相比纯水时电容的改变量为

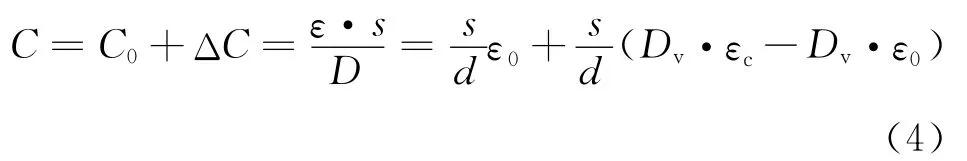
由于工业酒精跟水的介电常数差异较大，故不同浓度的酒精与水的混合物表现为不同的介电常数值，反映在电容上，即为电容量的不同，电容法测量酒精浓度正是基于这一原理．

由以上分析可知，只要测得电容量的变化ΔC，那么就可描述出进入电容内酒精的浓度变化，实验中采用测量电路将电容变化值转换为频率值，更直观的反映酒精浓度的变化趋势．

2 电容传感器的非线性修正

由以上分析可知，酒精所占的体积份额理论上与测量输出值成正比，但是实际测量时很多原因导致电容器非线性输出，这些因素包括：电容极板远不是理想的平行平板电容，极板的边缘效应很大；由于制造工艺与结构的影响．电容两极板的位置不可能完全对称，这使电容板间电场的分布更为复杂；另一方面引出线的引线寄生电容、接触电阻、金属材料的剩余磁场等，都导致了非线性影响结果．因此电容器输出出经常是呈现非线性．可采用曲线拟合法，来补偿非线性影响，曲线拟合法采用n次多项式逼近非线性曲线．

1）静态试验标定电容器及其测量电路．用m个已知浓度的混合溶液进行浓度测量，得到其对应的输出频率值．得到一组数据（d1，f1），（d2，f2），…，（dm，fm）．

2）确定输入非线性函数，设反非线性特性拟合方程为

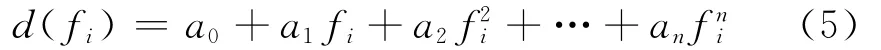
式中：a0，a1，a2，…，an为拟合函数的系数待定值，n的数值取决于离散点的非线性度，非线性度越大，n值应相应取较大的值，拟合结果也会精度提高．

3）求解待定常数．确定待定常数a0，a1，…，an的基本思路是，由式（5）确定各个d（fi）值与各个点的标定值di之均方差应最小，即函数F（a1，a2，…，an）的最小值．

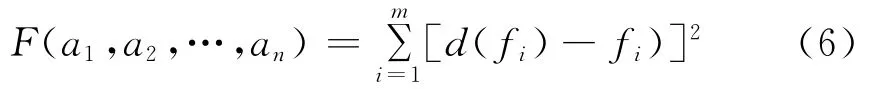
为了求得函数式（6）中，F（a1，a2，…，an）最小值时的常数，分别对F（a1，a2，…，an）的变量（a1，a2，…，an）求导，并分别令各个一阶导数为0，则可解出（a1，a2，…，an）为

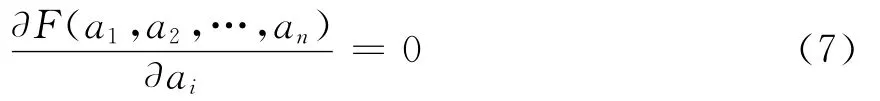
为了得到输出频率为f时所对应的被测酒精浓度值，每次只需将测量值f带入拟合方程便可求得浓度值d．

3 电容法测酒精浓度的实验验证

实验在常温常压环境中进行．本次实验的测量电路设计基于NE555组成的多谐振荡，电容法测量酒精浓度的框图如图2所示．设计思想是利用NE555时基集成电路与被测电容构成多谐振荡器，通过单片机对多谐振荡器的输出进行计数，得到电容值与振荡器输出方波频率之间的关系，从而通过判断方波频率得到被测电容的电容值．测量过程如下：电容对工业酒精浓度进行检测，电容两端的探头连接着NE555芯片，随着酒精浓度的不断变化，电容值改变，555芯片产生的不同频率的方波信号，单片机通过内部的计数器检测方波的频率值，最后将数据通过串口MAX232传送给计算机，计算机通过Matlab软件，对一组输入浓度值以及输出频率值进行非线性拟合处理，得到酒精浓度与频率输出的数学关系式．测量时应该尽可能的减少测量电路与电容器之间的距离，以减少线间电容的影响．

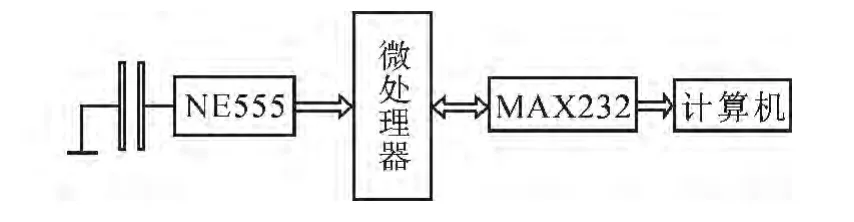
图2 系统方框图Fig．2 System diagram

4 实验过程及分析

实验采用Matlab软件中的polyfit来进行非线性拟合以及数据分析．实验过程中首先选择了40组不同体积分数的酒精和水混合作为实验的测量介质，混合物用量筒计量，得到实际酒精体积浓度值（酒精浓度值范围为12%～90%），经过测量电路的准换，得到与浓度值对应的电容频率值．表1为40组数据的实际浓度值D／%以及对应的频率值f．

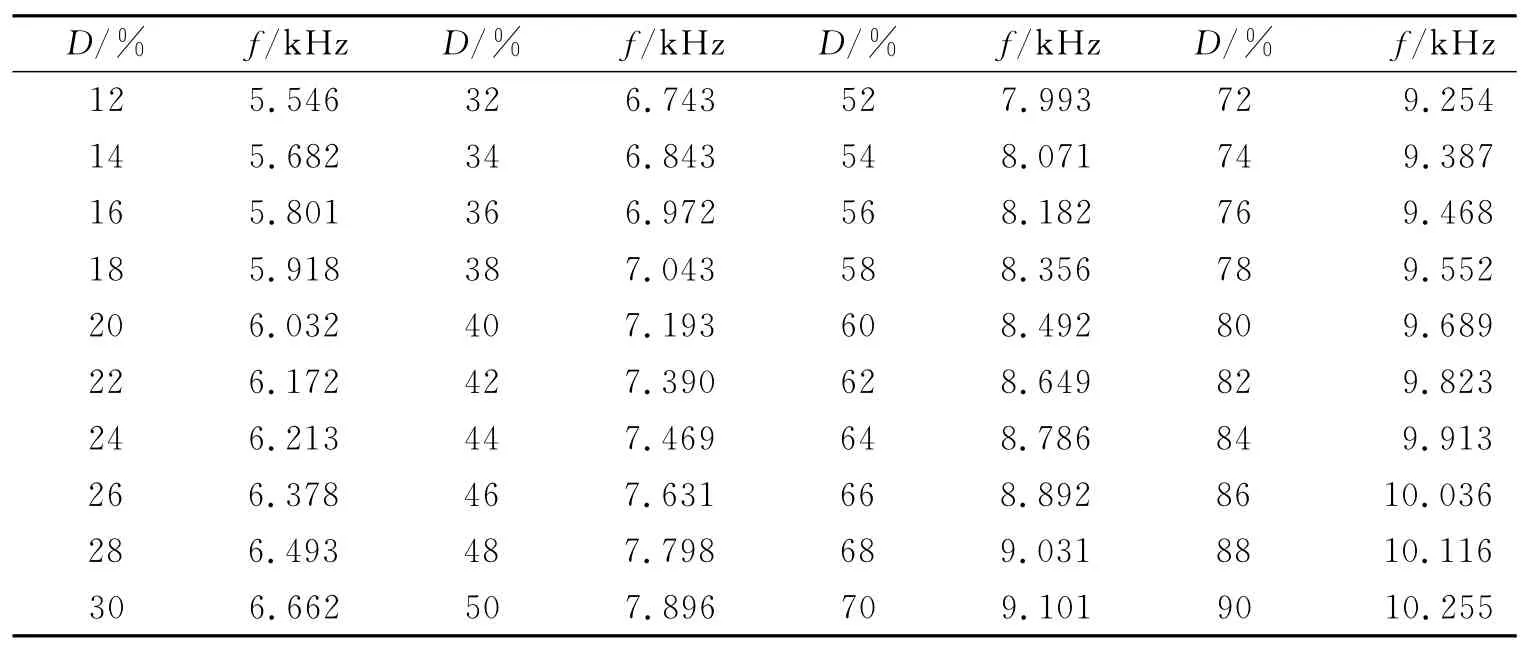
表1 40组实验数据Tab．1 40Groups experimental data

从表1所示的试验数据可知，工业酒精的实际浓度值与输出频率存在明显地相关性．为了求得相关模型，首先按照一元线性回归的方法来求得酒精浓度与频率值之间的的线性关系和模型，假设两者的线性关系模型为：D＝af＋b，其中a，b为线性关系式的系数．调用Matlab软件的polyfit函数得到系数a＝16．267 1，b＝-77．716 5，误差平方和为16．045 5，依照该关系模型求得各点理论值与实际值之间的相对误差曲线如图3所示．

分析图3可知，线性模型的误差较大，因此考虑使用非线性的方法进行误差校正，当拟合多项式的次数n分别取不同值时，得到不同的误差平方和值．图4为拟合次数分别为1～17时的误差平方和的仿真图．

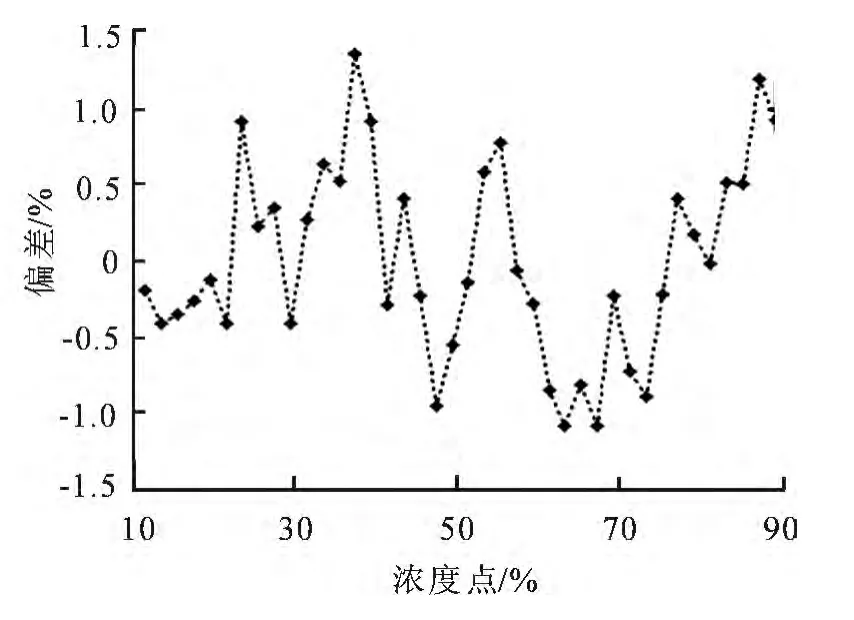
图3 一元线性误差Fig．3 A linear error

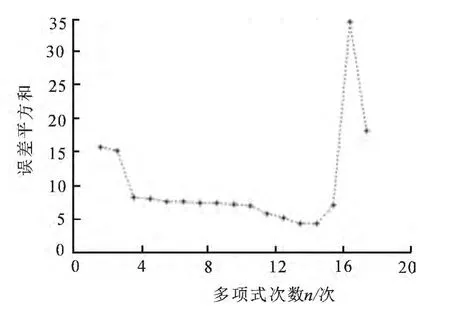
图4 不同n值的误差平方和Tab．4 Error sum of sguare for diferent nvalue

分析图4可知，当n＝13时，误差平方和最小，故取此时的拟合曲线作为输入输出的关系模型，依照该关系模型求得各点理论值与实际值之间的相对误差曲线如图5所示，此时的误差平方和为r13＝4．9653，与一元线性回归法测得的r1＝16．045 5相比，误差明显降低，各点的理论值与实际值的偏差基本分布于＋0．6%～ -0．6%之间，平均误差在0～0．3%之间，误差较小．

为验证非线性模型，在相同的浓度范围内利用同样的方法再选择5组酒精和水的混合液体进行测量．之后使用上述的拟合关系式，进行理论计算得到酒精的浓度值，并与实际的混合液体的的浓度值进行比较，计算该浓度值与实际值之间的误差，得到误差平方和为1．832 7，见表2，从结果可以看出，相比一元线性回归模型，该非线性数据拟合使得输出误差误差较小．

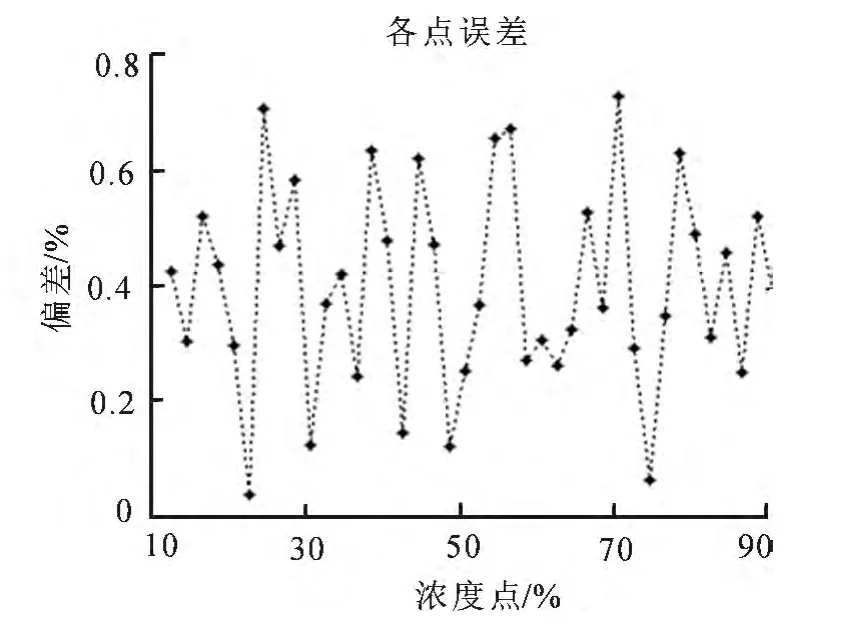
图5 n＝13时各点偏差Fig．5 Deviation of each point when n＝13

表2 5组测量结果Tab．2 5Sets of measurements

用Matlab软件来进行非线性拟合的实验结果说明，阶次为9，10，11，12，13，14时，其拟合曲线的均方差分别是7．681 8，7．501 6，6．382 9，5．776 5，8．760 9，8．513 7．取n＝13，误差平方和最小，当n继续增大时，误差增大且呈现不规律的变化，即开始出现最小二乘法的弊端．最小二乘法的对数据进行非线性拟合，尽管简单实用，但实际上是有一定的局限性的，处理结果不可能也没有必要完全达到理论上的拟合．

5 结 论

本文基于最小二乘法的寻优策略，以梯度为准则，提出了一种电容传感器非线性拟合数据处理算法，通过求得最小误差平方和，给出了工业酒精浓度随测量电路输出频率变化的数学模型．

利用该算法，能够消除电容传感器各种非线性因素对测量结果的影响，有效控制酒精浓度误差在0～0．3%范围内．为了有效降低测量误差，通过减小高次多项式病态特征，改善人为操作与环境因素对测量值的影响，以提高测量精准度．

［1］ 袁捷．基于51单片机的酒精浓度检测仪的设计［J］．电子设计工程，2013，21（18）：173．YUAN Jie．Design of the Alcohol Concentration Detector Based on 51Single-Chip［J］．Electronic Design Engineering，2013，21（18）：173．（in Chinese）

［2］ 杨建明，张佳薇．原油含水率测量PSO-BP非线性校正技术［J］．传感器与微系统，2008，27（5）：99．YANG Jian-ming，ZHANG Jia-wei．PSO-BP Nonlinear Calibration Technique for Petroleum Water Content Measurement［J］．Transducer and Microsystem Technologies，2008，27（5）：99．（in Chinese）

［3］ 王兆华．基于有源电桥的电容式传感器及其测量系统的研究［D］．北京：北京化工大学，2006．WANG Zhao-hua．Capacitive Sensors Based on Active Bridge Circuit and Its Measurement System［D］．Beijing：Beijing University of Chemical Technology，2006．（in Chinese）

［4］ 李杏华，樊玉铭．高精度电容式液位传感器的研究［C］／／2007仪表，自动化及先进集成技术大会论文集（一）．北京：仪器仪表学报杂志社，2007：15．LI Xing-hua．FAN Yu-ming．Research on High-Precision Capacitive Level Sensor［C］／／2007Instrumentation，Automation，and Advanced integration Technic Conference Proceedings（一）．Beijing：Scientific Instrument Magazine，2007：15．（in Chinese）

［5］ 樊尚春，梁虹．电容式固态物含水率传感器的模型［J］．仪器仪表学报，2004，25（S4）：1022．FAN Shang-chun，LIANG Hong．Mathematical Model of Capacitive-Type Moisture Sensor［J］．Chinese Journal of Scientific Instrument，2004，25（S4）：1022．（in Chinese）

［6］ 杨晓龙，陈孝友．电容法测液体高度和浓度实验［J］．四川工业学院学报，2000，19（1）：76．YANG Xiao-long，CHEN Xiao-you．Experimental Study on Liquid Height and Proportion［J］．Journal of Sichuan University of Science and Technology，2000，19（1）：76．（in Chinese）