升力式再入飞行器再入轨迹优化研究

王志刚，罗俏，李伟

(西北工业大学航天学院，陕西西安710072)

0 引言

近年来，美国正在逐步实现“弹道导弹防御”(BMD)计划，建立了战区导弹防御系统(TMD)和国家导弹防御系统(NMD)，这对采用常规再入的弹道式导弹提出了严峻的挑战［1］。针对弹道导弹防御系统不断发展的现状，再入式武器系统对各类防御系统的突防成功率是当前再入式武器系统技术发展的主要研究方向，对再入式武器提出了速度快、纵/横向机动性能强的要求，而传统的弹道式再入导弹很难满足横向大机动以及高精度打击敌对目标的要求，为此，各国开始研究一种升力式滑翔再入武器系统［2］。升力式再入飞行器再入突防速度快，在再入过程中能通过控制飞行器的再入迎角和倾侧角，改变飞行器的气动力，从而控制飞行器的飞行轨迹。与传统弹道式导弹相比，升力式再入武器系统具有更好的机动能力和较大的末端速度，能有效地避开敌方的防御系统，提高突防概率。在飞行器的研制初期，为了初步确定飞行器的机动能力，对飞行器升力式再入可行性进行验证，需对飞行器的再入轨迹进行优化研究。

国内外学者在飞行器再入轨迹优化方面已做了大量的研究工作，取得了令人瞩目的成果。传统的间接法能够快速得到较高精度的再入轨迹［3-4］，但需求解状态方程和协态方程，推导求解过程复杂，且对仿真初值敏感，很难收敛。相比间接法，直接法的收敛性对初值的设定具有更好的鲁棒性［5-6］，已经广泛地应用于轨迹优化问题中。直接配点法就是其中发展较为成熟的一种，其核心思想是采用多阶Gauss-Labatto积分公式将最优控制问题离散化处理为非线性规划问题，利用非线性规划方法进行求解。

本文采用三阶辛普森直接配点法和DFP算法对升力式再入飞行器再入轨迹优化问题进行求解，以得到一条横向机动距离大于3 000 km且具有较大末速的再入轨迹。

1 再入轨迹优化问题

1.1 飞行器无动力再入模型

将地球视为匀速旋转的圆球体，忽略地球自转的二阶小量，飞行器无动力再入在弹道坐标系下的质点无量纲运动方程［7］为:

式中，V，θT，σT分别为飞行器的速度、航迹角和航向角，用于描述飞行器的速度大小和方向;R，λ，φ分别为地心距、经度和纬度，用于描述飞行器在地心坐标系中的位置;地心距R、速度V、时间τ和地球自转角速度ω的无量纲化参数分别为地球平均半径为海平面处的引力加速度);¯X，¯Y分别为无量纲的阻力、升力加速度，表达式为:

式中，ρ为大气密度;Vc为地球第一宇宙速度;m0，S分别为再入飞行器的质量和气动参考面积。在计算大气密度和当地声速时，采用1976年美国标准大气模型［7］。在高超声速飞行条件下，飞行器的阻力系数CD和升力系数CL可以由气动力数据拟合为迎角和马赫数的函数曲线，可以大大增加优化程序的计算效率。

1.2 飞行器再入约束条件

1.2.1 弹道约束

高超声速飞行器再入过程中，由于飞行时间长、速度快、再入气动环境复杂，使得对飞行器在结构和热防护上需要较高的要求。为了满足飞行器在这些方面的可靠性，再入过程要求严格满足热流密度、动压和过载约束要求［8］。

式中，C1为与飞行器特性相关的常数;Rd为飞行器鼻锥驻点区的曲率半径;ρ0为海平面处的大气密度。对于大升阻比飞行器，其轴向和法向均可能产生较大的过载，文中考虑飞行器轴向和法向的总过载约束。

1.2.2 终端约束

考虑飞行器与末制导段交接班的要求，再入终端状态应满足一定的条件，包括等式约束(飞行器再入终端高度和经纬度的位置约束):R(τf)=Rf，λ(τf)=λf，φ(τf)=φf，以及不等式约束(终端航迹倾角的约束):θT(τf)＜0。

1.2.3 控制量约束

对于高超声速再入飞行器，在无侧滑的情况下无动力再入飞行，通过迎角α和倾侧角υ来调节控制。为了保证飞行器能稳定飞行，满足飞行器的控制能力，需要对控制量的幅值进行限制。

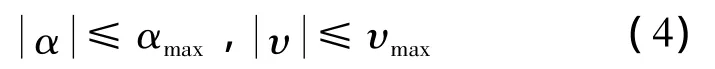
1.3 目标函数

根据飞行器再入飞行环境，在飞行器再入过程中，总的气动加热、动压和过载是需要极小化的量。同时，考虑飞行器的突防性能，将再入终端速度最大作为性能指标之一。因此，考虑如下的性能指标:

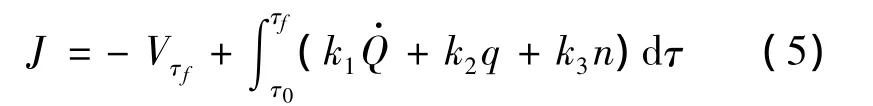
式中，ki(i=1，2，3)为权系数。

2 仿真计算与结果分析

2.1 仿真参数设置

飞行器总体参数:m0=852.139 kg，S=0.386 m2;再入初始条件:［V，θT，σT，H，λ，φ］=［7 200 m/s，－2°，40°，120 km，160°，5°］。热流密度约束:;动压约束:q≤500 kPa;过载约束:n≤4.0;控制量约束:|α|≤45°，|υ|≤50°;终端等式约束:［h(τf)，λ(τf)，φ(τf)］=［25 km，258°，38°］;终端不等式约束:θT(τf)＜0;性能指标:

2.2 仿真结果及分析

在轨迹优化过程中，采用三阶辛普森配点法对再入优化问题进行离散化处理［9-10］，将时间均分为40段，即取41个离散节点。在VC++环境下实现编程，利用DFP算法实现参数优化计算。优化得到的飞行器轨迹，最大热流量密度为448 kW/m2，最大动压为31 kPa，最大过载为2，均满足再入弹道约束的要求。优化得到的飞行器最优再入控制量如图1所示，再入轨迹各参数的变化曲线如图2～图4中的实线所示。将图1中优化得到的再入控制量代入飞行器的质心运动方程，迭代计算得到的飞行器再入轨迹各参数的变化曲线如图2～图4中的虚线所示。图5为优化和复现得到的飞行器再入速度方位曲线。

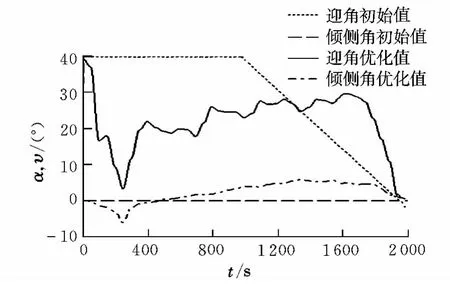
图1 飞行器再入控制量曲线Fig.1 Curve for vehicle’s reentry control variables

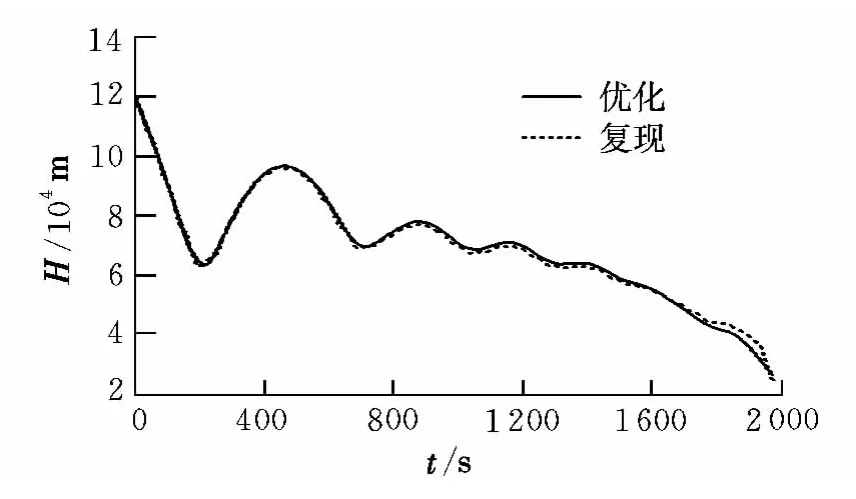
图2 飞行器再入高度曲线Fig.2 Curve for the vehicle’s reentry altitude

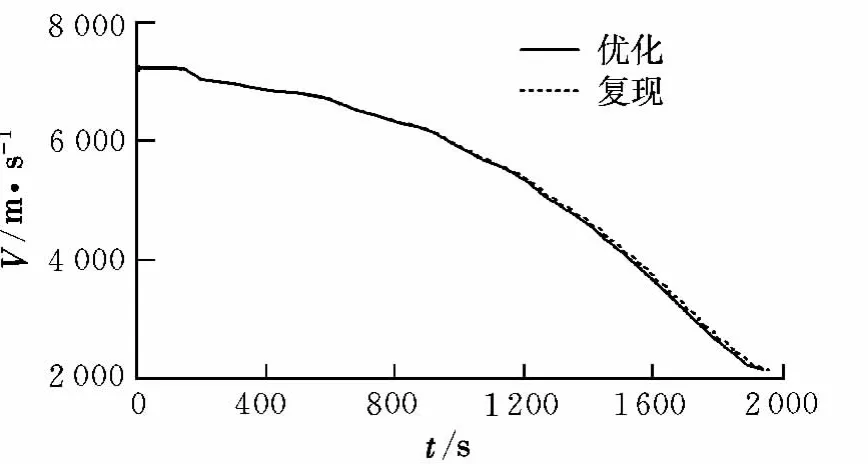
图4 飞行器再入速度曲线Fig.4 Curve for air vehicle’s reentry velocity

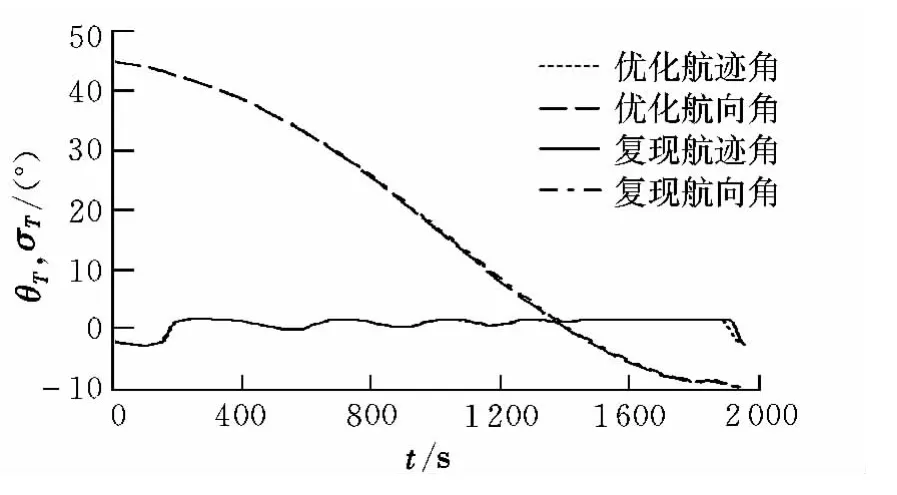
图5 飞行器再入速度方位曲线Fig.5 Curve for the air vehicle’s reentry velocity-azimuth

从图1中可以看出，优化得到的迎角和倾侧角的变化均较为平滑，都在控制约束值范围内。从图2～图4可以看出，优化得到的各状态量变化平滑，飞行器再入终端位置与约束值基本一致，说明优化结果有较高的精度，飞行器能实现高精度再入;同时，利用优化得到的再入控制量迭代复现得到的飞行器再入轨迹各参数变化与优化轨迹各参数基本一致，说明优化得到的再入轨迹是可控的。从飞行器的地面航迹可以看出，飞行器不仅有较大的航程(经度跨度100°，地面航迹超过104km)，横程也较大(纬度跨度达到35°，地面航迹约为3 880 km)，同时，飞行器的再入末端速度也较大，达到2 135 m/s。

3 结束语

本文基于直接优化方法中的辛普森配点法对升力式飞行器再入轨迹进行了优化求解，选取再入过程飞行器的加热率、动压、过载总作用最小以及再入终端末速度最大作为性能指标，在满足各种约束条件下，将迎角和倾侧角作为待优化控制量，得到再入最优轨迹。仿真研究结果表明，运用直接配点法对再入轨迹进行优化，可以得到一条高精度的再入参考轨迹，且飞行器的横程和末端速度均较大，利用优化得到的控制量可以迭代复现出最优再入轨迹，具有较高的实际应用价值。本文的研究成果可以进一步应用到飞行器的再入制导控制问题中。

［1］ 孙连山.导弹防御系统［M］.北京:航空工业出版社，2005.

［2］ 胡正东.天基对地打击武器轨道规划与制导技术研究［D］.长沙:国防科学技术大学，2009.

［3］ Shen Z J，Lu P.On-board entry trajectory planning expanded to sub-orbital flight［R］.AIAA-2003-5736，2003.

［4］ 陈有容，袁建平，罗建军.再入滑翔式飞行器轨迹快速优化［J］.飞行力学，2008，26(6):47-51.

［5］ Timothy R.Three dimensional trajectory optimization satisfying waypoint and no-fly zone constraints［J］.Journal of Guidance，Control，and Dynamics，2009，32(2):551-572.

［6］ 雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究［D］.长沙:国防科学技术大学，2008.

［7］ 张毅，肖龙旭.弹道导弹弹道学［M］.第二版.长沙:国防科学技术大学出版社，2005:12.

［8］ 何烈堂.跨大气层飞行器的热力学环境分析与飞行规划研究［D］.长沙:国防科学技术大学，2008.

［9］ 涂良辉，袁建平.基于直接配点法的再入轨迹优化设计［J］.西北工业大学学报，2006，24(5):653-657.

［10］ Herman A L，Conway BA.Direct optimization using collocation based on high-order gauss-lobatto quadrature rules［J］.Journal of Guidance，Control，and Dynamics，1996，19(3):592-599.