高空太阳能弹性无人机纵向动力学特性研究

冯扬帆，周洲，肖伟

(西北工业大学无人机特种技术国家重点实验室，陕西西安710065)

0 引言

高空太阳能无人机具有展弦比大、结构重量轻、结构刚度小、在飞行过程中机翼变形明显等特点，如“太阳神”无人机在极限状态下的机翼上反角可达到50°［1］。大展弦比弹性无人机的机翼结构振动频率低，与无人机运动模态频率接近，存在明显的动力学耦合，所以其动力学特性相比常规飞机有很大的不同。

目前飞行力学中常用的弹性飞机模型是基于机翼为匀质、单方向变形假设推导的，使用同一坐标描述，该模型对于发生大幅度变形的大展弦比太阳能无人机来说不再适用。文献［2］基于几何精确完全本征梁模型，建立了大展弦比柔性飞机的动力学模型，并对气动弹性与飞行动力学耦合配平、动稳定性和时域响应特性开展了研究。文献［3］将整个无人机看作Hodges梁［4］，并基于Hamilton原理对大展弦比弹性无人机进行了动力学建模，得到了局部坐标系下的状态方程，但并没有详细论证状态方程从局部坐标系到整体坐标系的转换，也没有通过模态特性研究其纵向动力学特性。

局部坐标系可以使大展弦比无人机建模过程大为简化，但却不利于分析研究无人机整体的动力学特性。本文将无人机局部坐标系下的状态方程转换到平均轴坐标系与结构模态坐标系组成的整体坐标系下，消去高频结构模态，在不同的状态点对弹性无人机进行分析，通过弹性无人机特征根分布研究了弹性无人机的纵向动力学特性。

1 整体坐标系下的状态方程

无人机局部坐标系下的状态方程为:

式中，Δx=［Δu1，Δχ1，ΔV1，Δω1，…，Δun，Δχn，ΔVn，Δωn］，其中Δu，Δχ，ΔV，Δω 分别为无人机每一段在局部坐标系下的线位移、角位移、速度和角速度。需要建立一个由平均轴坐标系与模态坐标系组成的整体坐标系，用来描述无人机整体的平动、转动和结构变形，并且使无人机整体的平动、转动与无人机弹性变形运动在动力学上分离开来。

1.1 平均轴坐标系下的动力学方程

将无人机的每一段独立研究，弹性力当作外力处理，把无人机看作多刚体系。考虑n个刚体组成的多刚体系，第i个刚体的质量为mi，在每一个刚体上建立自身参考系bi。在其自身参考系内，转动惯量为Ii，速度为Vi，角速度为ωi，内力和内力矩为Fi和Mi。针对该刚体系，任意建立一个统一的参考系a，设其原点在地面坐标系内的位移为Ra，第i个刚体在a坐标系内的位移为ri，在地面坐标系的位移为Ri，则Ri=Ra+ri。通过两种不同的形式表示出多刚体无人机的总动量:

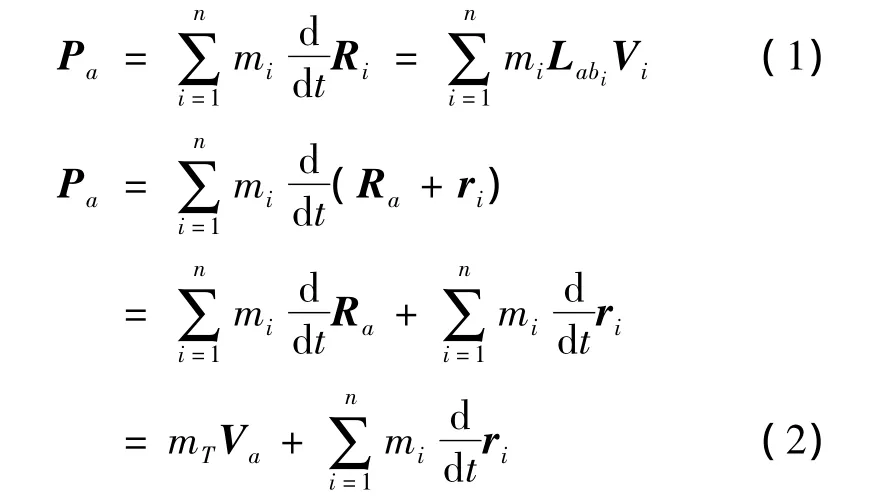
式中，mT为刚体系统的总质量;Va为多刚体系在a参考系内的速度;Labi为第i个刚体参考系bi到参考系a的转换矩阵。设这一系列刚体的质心在a参考系内的位移为ξa，d/d t表示在惯性系内求导，可得:

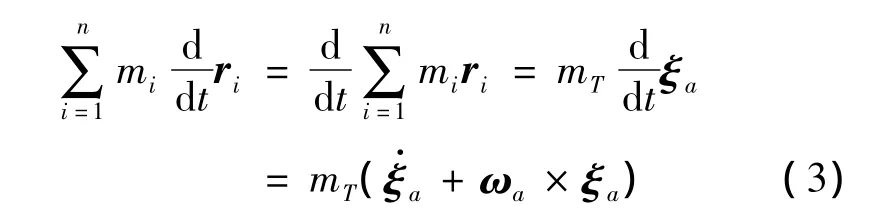
则对式(1)、式(2)求导可得:

如果将参考系a的原点始终取在刚体系的质心处，即ξa=0，这样a参考系下的多刚体运动速度和动量可以简化为:

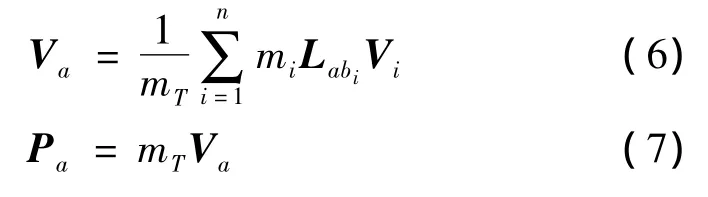
把参考系a的原点取在无人机质心处，则a参考系为所要用到的平均轴坐标系m。由式(4)、式(5)得到平均轴坐标系内的动力学方程为:

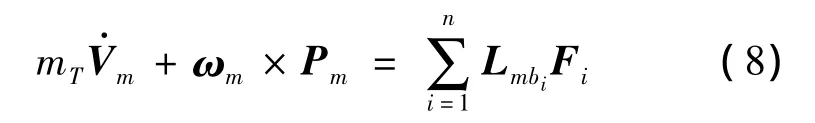
平均轴坐标系内配平状态的小扰动运动学方程为:

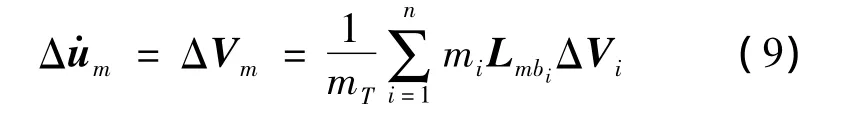
以上两式为平均轴坐标系下的平动运动关系。同理可得转动运动的关系式:

式中，Hm=Icgωm表示在平均轴坐标系下的刚体的角动量;表示多刚体系对质心的转动惯量。

1.2 结构变形模态的计算

采用局部坐标系来描述无人机的结构变形，即使在线性化后，得到描述变形运动的阶数还是很高，也难以分析。在本文中，需要通过模态的概念对结构变形进行描述，因此需要计算无人机的结构模态，得到无人机结构的结构模态特征值和特征向量。首先将无人机的动能与势能描述为:

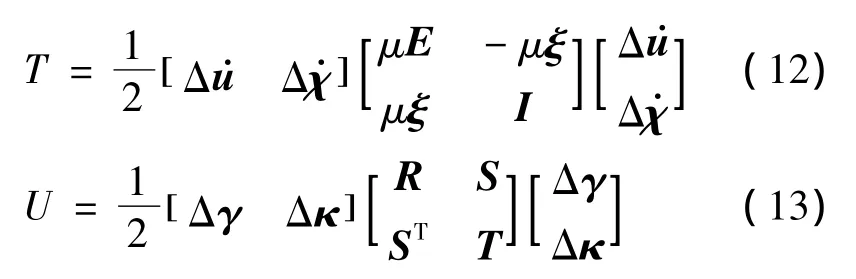
式中，Δγ，Δκ［5］分别为 Hodges梁假设中定义的线应变和角应变，可以用线位移Δu、角位移Δχ描述;μ为翼段的质量;E为单位矩阵;ξ为翼段质心在局部坐标系下的位置向量;R，T分别为翼段的剪切刚度和扭转刚度;S为0矩阵;I为翼截面相对翼段刚心的惯量矩阵。

根据Hodges梁的建模思想，在局部坐标系内将无人机的虚位移表示成q=［Δu，Δχ］T，通过式(12)和式(13)建立不考虑外激励和阻尼力的保守系统的拉格朗日方程:

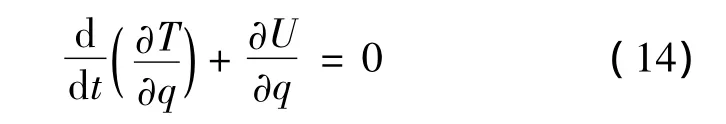
由式(14)可以得到结构运动方程:

式中，Mm，Ms分别为无人机的结构质量矩阵和刚度矩阵。通过求解该方程得到结构特征值与特征向量，这样就在配平状态下得到了无人机结构模态的特征值和模态矩阵［6］。

1.3 坐标体系转换

首先给出无人机在局部坐标系内的位移扰动量Δse=［Δu1，Δχ1，…，Δun，Δχn］T，其与无人机各阶结构模态的模态坐标Δsh的对应关系为:

式中，μ1由系统非零根对应的特征向量得到。由式(9)和式(11)，可以将局部坐标系内的位移扰动量转换到平均轴坐标系内描述无人机与结构模态解耦的刚体自由度运动:

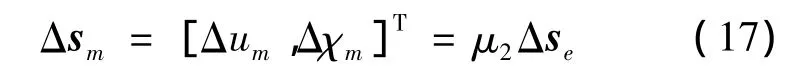
式中，μ2由平均轴转换矩阵Lmbi得到。由式(16)和式(17)，可以将无人机局部坐标系内的状态量转换为无人机平均轴坐标系与模态坐标系下的状态量:

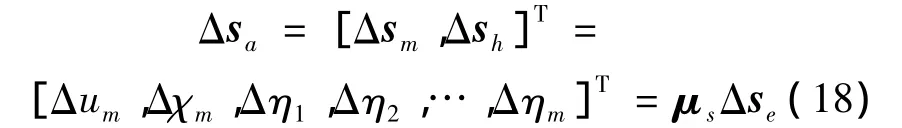
式中，转换矩阵 μs由 μ1，μ2得到，这样物理概念更明确，且减小了各状态量之间的耦合;Δη为弹性无人机结构模态坐标;Δsh为从低频到高频排列的模态坐标。以上得到了位移向整体坐标系的转化，同理将无人机局部坐标系的速度转化到整体坐标系下:

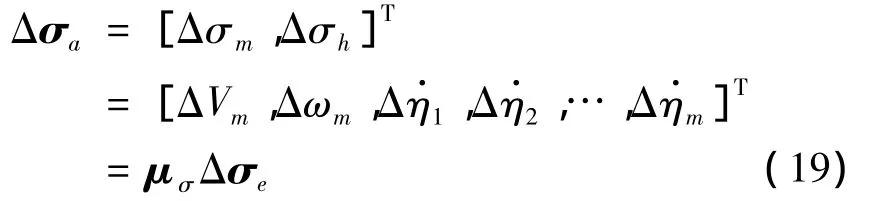
2 纵向动力学特性分析

给定高空太阳能弹性无人机的布局、结构以及气动参数，经过配平计算，选取一阶结构模态，得出状态矩阵Alon，通过求解状态矩阵的特征根来分析弹性无人机的动力学特性。选取不同的状态点，对弹性无人机与刚性无人机进行对比，并对弹性飞机的飞行品质进行研究。选取的状态点为:FC1～FC5是无人机载重量一定(96 kg)，飞行高度分别为5 km，10 km，15 km，20 km，25 km 的状态点;FC6 ～FC10是无人机飞行高度一定(20 km)，载重量分别为 0 kg，50 kg，100 kg，150 kg，200 kg 的状态点。

2.1 弹性无人机与刚性无人机的对比

首先将弹性无人机的状态方程与刚性无人机的六自由度方程进行比较，计算它们各自在20 km高度，载荷由0～200 kg特征根的分布情况。图1为刚性、弹性无人机长周期特征根分布比较。

图1 长周期特征根分布比较Fig.1 Root locus of phugoid mode

由图1可以看出，随着载荷的增加，刚性无人机的长周期特征根变化很小，而弹性无人机的特征根变化很大，这说明弹性无人机的结构变形对无人机的动力学特性有很大程度的影响。

2.2 弹性无人机飞行品质研究

2.2.1 长周期模态

按GJB185-86中飞机纵向长周期速度振荡应满足的要求，分析弹性无人机的飞行品质。因为以上标准是针对飞机制定的，飞机在遇到长周期发散模态时驾驶员易于控制，但是这种情况无人机却难于控制，所以飞行品质标准应高于飞机，暂且把标准2定为长周期稳定的最低标准［7］。图2为FC1～FC5长周期特征根分布情况。

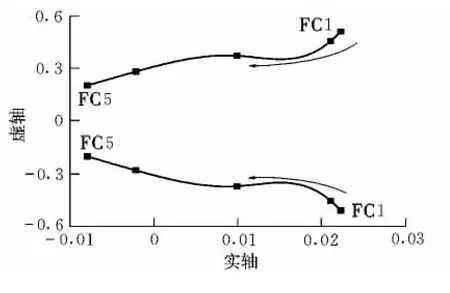
图2 长周期特征根分布情况Fig.2 Root locus of phugoid mode

由图2可以看出，无人机的长周期阻尼比随着飞行高度的升高，由负变正，由不稳定变为稳定;无人机在5 km，10 km，15 km的高度阻尼比为负;在20 km(FC4)高度的长周期飞行品质达到标准2;在25 km(FC5)高度的长周期飞行品质接近标准1。因为在低空相对高空模态频率较高，与结构频率更接近，所以与结构模态的耦合会比在高空更大，所以低空的飞行品质要比高空的差。

由图1还可以看出，在FC6～FC10，无人机的长周期阻尼比在20 km的高度随着载重量的增加，由正变负，由稳定变为不稳定。FC6长周期飞行品质要求达到标准1，FC7和 FC8达到标准2，FC9和FC10长周期不稳定。这说明随着载重的增加，无人机的变形加剧，长周期模态与结构模态的耦合作用加大，在无人机长周期运动中不仅存在动能与重力势能的转换［8］，同时还包括了动能与弹性势能的相互转换，结果导致了长周期模态稳定性的降低。

2.2.2 短周期模态

图3为FC1～FC10短周期特征根的分布情况。

图3 FC1～FC10短周期特征根分布情况Fig.3 Root locus of short period mode for FC1 ～ FC10

同样采用GJB185-86中规定飞机短周期阻尼比ξp应满足的要求进行分析，所有状态均满足标准1。在FC1～FC5，随着高度的增加短周期阻尼比不断降低，这是因为随着高度的升高，俯仰阻尼随空气密度的减小而减小，飞行品质逐渐变差。FC6～FC10载重量的变大使短周期阻尼比逐渐变大，飞行品质逐渐变好，这是由于载重量的变大、载重的集中，使得机翼的上弯加剧，所以无人机的俯仰转动惯量增加，短周期运动的阻尼比也增大。如果挂载的弦向位置发生改变，转动惯量的变化更大，阻尼比会更大。

3 结束语

本文得到了平均轴坐标系描述无人机整体运动、模态坐标系描述结构变形运动的无人机状态方程，整体坐标系下的状态方程便于进行动力学特性研究。通过对状态矩阵的模态分析，研究了弹性无人机的动力学特性，发现弹性无人机在长周期模态，因为动能与弹性势能相互转换，使长周期运动特性恶化;短周期运动则由于弹性变形，机翼上弯从而增加了弹性无人机的俯仰转动惯量，短周期运动阻尼比也随之增加，改善了弹性无人机的短周期运动特性。

［1］ 肖伟.高空太阳能无人机动力学建模和控制方法研究［D］.西安:西北工业大学，2013.

［2］ 张健，向锦武.柔性飞机非线性气动弹性与飞行动力学耦合静、动态特性［J］.航空学报，2011，32(9):1569-1582.

［3］ 肖伟，周洲.高空太阳能无人机飞行动力学建模与分析［J］.飞行力学，2012，30(5):385-388.

［4］ Patil M J，Hodges D H.Flight dynamics of highly flexible flying wings［J］.Journal of Aircraft，2006，43(6):1790-1798.

［5］ Hodges D H.Geometrically exact，intrinsic theory for dynamics of curved and twisted anisotropic beams［J］.AIAA Journal，2003，41(6):1131-1137.

［6］ Giulio Romeo，Giacomo Frulla.HELIPLAT:aerodynamic and structural analysis of HAVE solar powered platform［R］.AIAA-2002-3504，2002.

［7］ 王睿.飞翼式高空长航时无人机飞行控制与仿真研究［D］.西安:西北工业大学，2008.

［8］ 方振平，陈万春，张曙光.航空飞行器飞行动力学［M］.北京:北京航空航天大学出版社，2005:288-301.