基于改进差分进化算法的PIO预测评估方法

李琳，陈云翔，李千，纪小柠

(1.空军工程大学 机要系，北京100195;

2.空军工程大学装备管理与安全工程学院，陕西西安710051;3.空军装备部，北京100843;4.空军指挥学院，北京100097)

0 引言

随着高增益电传操控系统在现代飞机上的广泛应用，PIO发生的概率不断增加［1］，至今已造成多起机毁人亡的事故。因此，如何通过系统、高效的方法对PIO进行预测评估，是飞机研发阶段和飞行安全保障工作中面临的重要课题。目前国外已研发出多种PIO预测准则，为新型飞行器的研发和飞行控制系统设计、解决PIO问题、保障飞行安全提供了重要的理论依据。从国内研究现状来看，PIO领域的研究仍处于理解和运用国外已有准则和方法阶段，并且对PIO预测评估方法的研究不系统，缺少验证PIO预测准则的飞行模拟与飞行试验，未建立类似于国外的PIO评估数据库，与国外仍然存在不小的差距。我国在该领域仍需进一步展开研究，以使我国的飞行器安全性设计水平与国际接轨。

本文提出了一种基于改进差分进化算法的PIO预测评估方法，以速率限制II型非线性PIO为例，构建了基于速率限制因素的人机闭环系统模型，根据Gap准则运用该算法对人机系统PIO进行预测评估。

1 改进型差分进化算法

目前全局搜索优化算法主要包括遗传算法(GA)、粒子群进化算法(PSO)和差分进化算法(DE)。与其他两类优化算法相比，DE算法结构简单，便于操作，经验型参数设置最少，且DE算法的收敛和优化效率相对优于GA和PSO算法。但基本型DE算法的参数被预先设定，并且在优化过程中一成不变，很难实现算法搜索与开发能力的平衡。针对DE算法的局限性，提出了一种基于混沌理论与高斯扰动的改进型差分进化(Differential Evolution Based on Chaos Theory and Gaussian Disturbance，CTGDDE)算法，图1给出了该算法的流程图，具体步骤与算法性能验证见文献［2］，其基本思想是通过引入混沌理论进行局部搜索以提高算法的寻优能力;通过在交叉阶段引入高斯扰动算子来防止算法陷入局部最优，从而兼顾实现算法的局部寻优和全局寻优。

图1 CTGDDE算法流程图Fig.1 Process of CTGDDE algorithm

2 PIO预测评估方法

人机系统PIO预测评估的最终目的是确认所设计的控制系统能够保证飞机在所有飞行包线和飞行参数变化范围内都能匹配飞行员特性并安全稳定地完成任务，同时具有良好的飞行品质。具体而言，基于CTGDDE算法的人机系统PIO预测评估问题可描述为针对人机系统PIO评估的相关准则，根据具体的飞行任务建立人机系统闭环模型，设计并求解适应度函数的优化问题，进而搜索最坏情况及其人机系统状态参数的集合，从而给出评估结论及设计更改建议，其具体步骤如下:

(1)初始化。确定待评估的飞行状态，根据飞行任务与设计要求设置人机系统不确定状态参数及其变化范围;

(2)根据飞行任务和飞行状态建立相应的飞行员控制行为模型、飞机本体动力学模型及其传递函数和控制系统模型，并构建该模式下的人机闭环回路;

(3)确定人机系统PIO预测评估准则，根据人机闭环模型建立相应的适应度函数，即将人机系统PIO评估转化为适应度函数的优化问题;

(4)将标称状态的参数值代入适应度函数，检验飞行控制系统的设计是否与飞行员特性相匹配，即该设计是否满足人机PIO准则的要求。若均满足，则执行步骤(5)，否则该设计未达标，转入步骤(7);

(5)通过文献［2］提出的CTGDDE算法对适应度函数展开优化运算，即在不确定参数变化空间内搜索飞行状态最坏情况下的参数集合;

(6)根据最坏情况下的适应度函数值判断该情况下的控制系统设计是否满足人机系统稳定性要求，若满足，则保存分析结果，否则该控制系统设计未达标;

(7)转入下一飞行状态进行评估;

(8)遍历飞行包线范围内所有飞行状态，若所有状态均满足人机PIO准则要求，则该飞行控制系统设计通过该准则确认，否则未予确认，需进行改进后再予以评估。

需要注意的是，为了更全面准确地对控制系统进行评估，通常采用多个人机系统PIO预测准则对其进行验证;在人机闭环系统建模方面，也应考虑实际任务的多样性，结合多种飞行员控制行为模式对飞行控制系统展开评估。

3 模型的建立

由于PIO属于人机闭环不稳定振荡，故闭环操纵是其必要条件。因此，构建人机闭环控制系统模型是研究PIO问题的基础。本文对基于速率限制环节的Ⅱ型PIO进行预测评估，首先要建立基于速率限制因素的人机闭环系统模型，其俯仰轴模型如图2所示。

图2 基于速率限制因素的人机闭环系统模型Fig.2 Human machine system model based on rate-limit

图2 中，速率限制舵机模型可进一步分解，如图3 所示［3］。

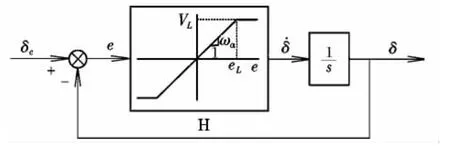
图3 舵机速率限制模型Fig.3 Rate-limit model

操纵面偏角指令δc经速率限制模型后输出操纵面偏角信号δ，通过偏角的实时反馈信息，使之形成闭环回路，其中前向通道误差信号e=δc－δ作为非线性饱和环节H的输入，饱和模块的输出是操纵面速率δ˙，通过对该信号进行积分运算可得到操纵面偏角信号δ。非线性饱和模型H可通过以下3个参数进行描述:饱和值VL，即舵机速率的限制值;增益值ωα，即模型H中线性部分的斜率，其值等于线性舵机闭环带宽或简化等于线性带宽;速率饱和阈值eL=VL/ωα，当前向通道输入的误差值e＜eL时，环节H可简化为线性一阶滞后模型，其响应取决于时间常数T=1/ωα。相应地，当输入误差值e＞eL时，操纵面速率限制环节将被激活，该模式下会呈现出完全的非线性，其特点是。有研究表明，该模式下的响应特性完全独立于线性部分的时间常数T，而取决于其输入幅值与速率限制，非线性与线性时间常数比满足如下关系式:

在实际研究中，通常采用描述函数的方法来研究速率限制模型等非线性系统，当输入信号δc=A sin(ωt)时，舵机速率限制模型中的饱和非线性环节可描述为:

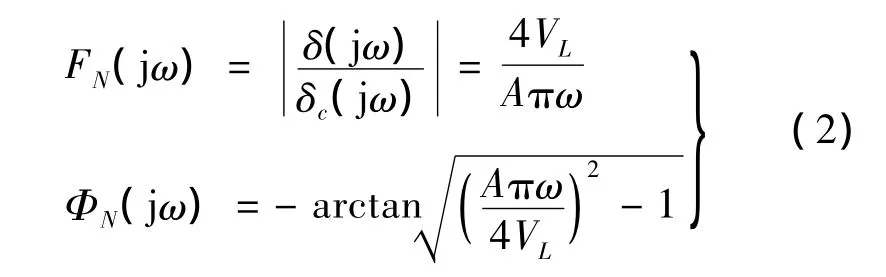
式(2)也称为速率限制作用下舵机高度饱和时的正弦输入描述函数模型，其形成的机理是由于输入误差值在大多数时间大于速率饱和阈值eL，造成系统长时间处于非线性状态。相应地，当输入误差在少数时间超过eL时，系统输出仅间断性地出现速率限制，其响应呈现拟线性特征，该模式称之为近饱和状态，此模式下的正弦输入模型可描述为［4］:

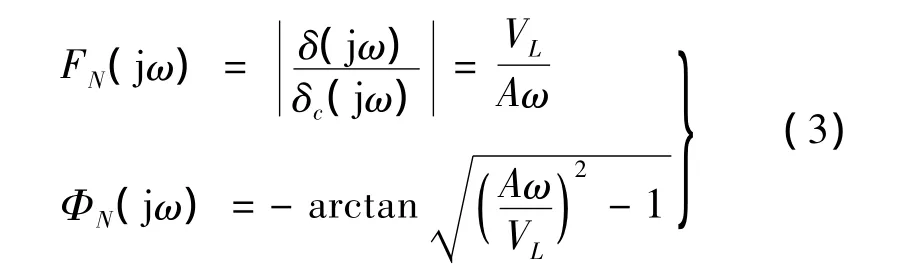
当速率限制高度饱和且舵机带宽趋于无穷时，高度饱和正弦输入模型可描述为正弦输入/三角输出的近似描述函数模型，具体表述为［5］:

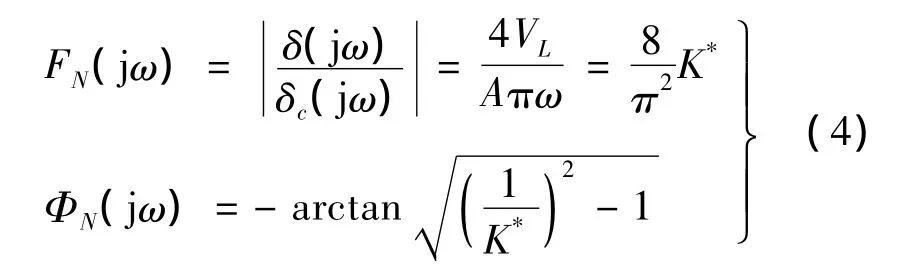
这里引入参数 K*= πVL/(2Aω)= πTωα/(2TNω)，且 K*∈［0，1］，其数值反映了系统速率限制的严重程度，当K*→0时，速率限制作用增强，系统呈现非线性，表现为幅值衰减，相位滞后增加;相应地，当K*→1时，速率限制作用减弱，系统的线性部分增强。

对比式(2)、式(3)和式(4)，不难发现，前两式仅差一个比例常数π/4;而第3式的幅频函数与第1式相同。实践表明，在三者的应用方面，需满足以下条件:

(1)当0.2≤T/TN＜0.8时，采用高度饱和正弦输入描述函数模型;

(2)当T/TN≥0.8时，采用近饱和正弦输入描述函数模型;

(3)当T/TN＜0.2时，采用正弦输入/三角输出描述函数模型。

4 实例分析

本文选用Gap准则对Ⅱ型PIO进行预测评估，Gap准则及其使用规范在文献［6］中有详细叙述，在此不加赘述。假设某飞机舵机带宽为ωα=35 rad/s，速率限制值为VL=30(°)/s，最大可用偏角值Amax=30°。在飞机线性运动模型方面，选取该型飞机在高度为1.5 km，马赫数为0.2处为标称状态，设定飞机质量、y轴转动惯量、气动参数和为摄动参数，该机型在标称状态下的俯仰传递函数为:

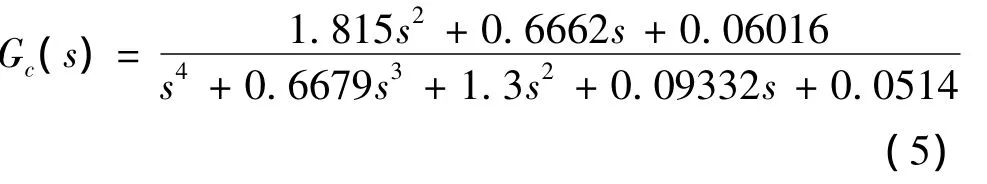
根据传递函数可求出飞机的中性稳定频率ω0=9.5 rad/s。由于ωα≫ω0，飞机舵机可认定为满足无限带宽条件，因此，可选择正弦输入/三角输出描述函数为飞机舵机的数学描述模型。

大量事实表明，Neal-Smith飞行员模型在一定程度上可以较全面地反映飞行员的控制特性，根据美军标中关于Neal-Smith飞行员驾驶模型的确定准则，建立飞行员驾驶模型为:

首先通过Matlab 2010a可获得Gc(s)Gp(s)与速率限制舵机负倒数描述模型F(A，jω)的Nichols曲线，如图4所示。

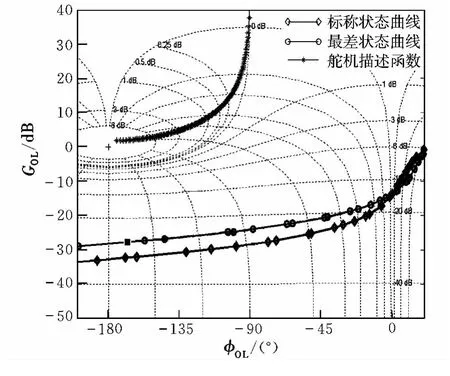
图4 标称情况与最差情况下的Nichols曲线Fig.4 Nichols curves of the normal case and the worst case

根据Gap准则可知，该情况属于Ⅰ类应用模式，求解使两条曲线恰好相切时飞行员需增加的有效增益的最小值ΔKp=34.3842 dB，相对应的K*=0.9675，ω=16.4 rad/s。因此，根据 Gap准则可计算出导致PIO的飞机舵机偏角幅值为:

通过Gap准则，可计算出标称状态下的准则参数G为:

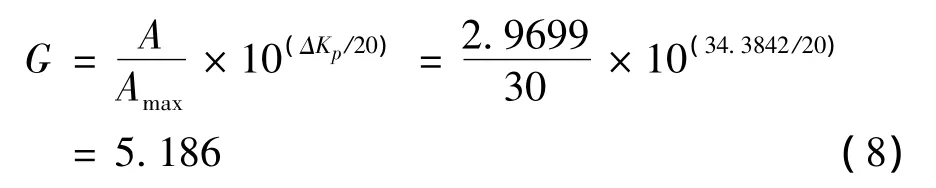
由于G＞1，因此，飞机在设计点处符合准则要求。根据Gap准则，构建Ⅰ类应用模式下的适应度函数模型:

设置CTGDDE算法的参数 T=30，M=60，q=0.2，η=0.1，C=0.9，假设摄动参数在标称值上下15%范围内浮动，运用Matlab编程迭代搜索8次即可使适应度函数的最小值稳定至f=2.0205＞0。图5给出了算法的寻优曲线。由图5可知，该系统满足准则要求。此时 ΔKp=29.8339 dB，ω=16.5 rad/s，K*=0.9778，适应度函数最小值对应的最差状态下的Nichols曲线见图4。图4中，最差状态处的增益为 －27.8 dB，相位为 －168°，频率为16.5 rad/s。

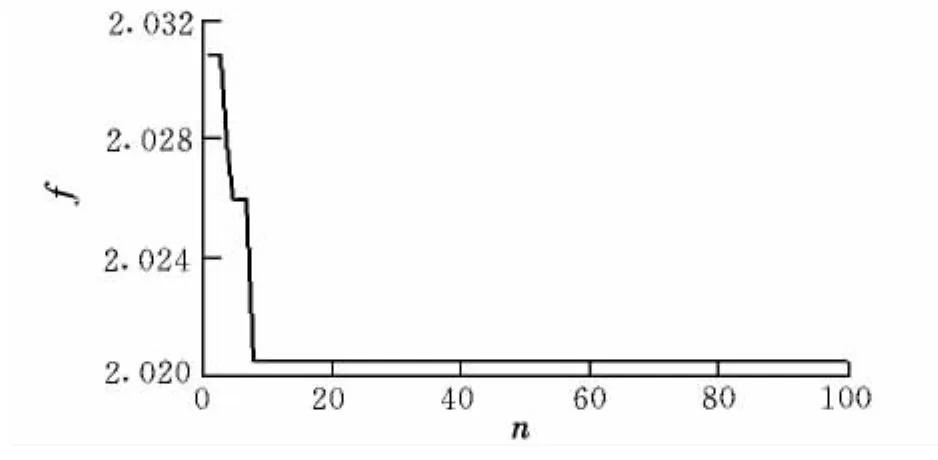
图5 CTGDDE算法寻优曲线图Fig.5 Optimization curve of CTGDDE algorithm

5 结束语

传统的人机系统稳定性评估通常根据评估准则对飞行包线内设计点处的情况进行确认，而设计点间的情况只能借助于复杂的仿真运算，而且难以应对多参数同时变化的情况。针对上述不足，本文以控制系统中速率限制因素为例，建立相应的人机闭环系统模型，进而根据Gap准则利用CTGDDE算法对该情况下的人机PIO进行评估。该项研究为飞机研发阶段PIO预测提供了一种新型高效的评估方法。

［1］ Liebst B S.Nonlinear pre-filter to prevent pilot-induced oscillations due to actuator rate limiting［J］.Journal of Guidance，Control，and Dynamics，2002，25(4):740-747.

［2］ 陈云翔，李琳，李千，等.基于改进差分进化算法的飞行控制律评估方法［J］.航空学报，2013，34(6):1261-1268.

［3］ 胡新江，胡浩军，李大伟，等.速率限制舵机描述函数模型研究［J］.飞行力学，2011，29(5):14-17.

［4］ Ashkenas I L，Jex H R，McRuer D T.Pilot-induced oscillations:their causes and analysis［R］.Northrop-Norair Report，1964.

［5］ Hanke D.Handling qualities analysis on rate limiting elements in flight control systems［R］.Europe:AGARDAR-335，1995.

［6］ 孟捷，徐浩军，张建康，等.Gap准则在II型PIO预测中的应用［J］.北京航空航天大学学报，2010，9(4):1067-1070.