增升装置低速流动特性的雷诺数效应计算研究

李中武，梁益华

(西安航空计算技术研究所第七研究室，陕西西安710019)

0 引言

大型运输类飞机低速增升装置设计是设计开发中的重要部分，了解增升装置流动特性，掌握流场结构，对于设计出更高效率的增升装置系统是十分重要的。低速增升装置系统是一个多元复杂系统，各个部件存在着尾流(迹)及尾流干扰、流动分离等复杂的流动现象［1］。由于风洞条件限制，大型运输类飞机风洞试验均采用缩比模型，试验雷诺数与自由飞行雷诺数达到1～2个数量级的差别。高和低雷诺数状态下，飞机流场的流动状态可能存在很大不同，气动力与力矩特性也会存在差异。对大型运输类飞机来说，从翼根到翼梢的气动弦长变化很大，当地雷诺数变化明显，气动力和流动特性对雷诺数变化更为敏感［1］。

当前CFD已经应用于飞行器的设计、鉴定和优化等环节。复杂构型的流动分析，甚至风洞流场分析可以借助CFD数值模拟［2］，利用CFD技术进行低速增升构型流动特性的雷诺数效应影响研究成为可能。欧盟第六次气动研究框架计划组织多家单位采用CFD和风洞试验结合进行雷诺数效应研究［3-4］;波音公司在 B787的开发过程中，也采用CFD、风洞试验和飞行测试等方法研究了雷诺数效应对飞机气动力和流动特性的影响。

本文采用CFD方法求解雷诺数平均方程，数值模拟风洞试验低雷诺数到飞行雷诺数范围内的增升装置的绕流流场，研究雷诺数对增升装置各部件流动特性的影响规律，分析由此引起的气动力特性的变化，并与风洞试验结果进行比较，为大型运输类飞机增升装置设计和风洞测试数据修正提供参考。

1 计算方法

求解的主控方程为无量纲可压缩三维N-S方程，其守恒型向量形式可写成:

湍流模型采用Menter-SST模型，属于积分到壁面的不可压缩/可压缩湍流的两方程涡粘性模型。SST模型通过引用一个混合函数将k-ω和k-ε模式合并为一种模式，既发挥了k-ω模型在近壁附近的稳定性，又利用了k-ε模式在边界层外部的独立性。

转捩模型采用γ-Reθ模型，此模型将经验关联转捩模拟方法和间歇因子转捩模拟方法有机结合，通过把动量厚度雷诺数与当地的最大应变率关联，回避了动量厚度的计算，通过Reθ输运方程实验模型计算的当地化，将经验关联转捩模拟方法融入到现代CFD数值模拟。

2 算例分析

2.1 模型几何与网格

测试算例采用标准模型和真实飞机增升装置构型。如图1所示，Trapwing高升力机翼模型是NASA先进亚声速技术的高升力项目采用的标准气动模型，具备大量比较可靠的气动力和力矩测试数据［5］。图2为某民机增升装置着陆构型的几何示意图。

图1 Trapwing半展风洞试验模型Fig.1 Trapwing half span model in wind tunnel

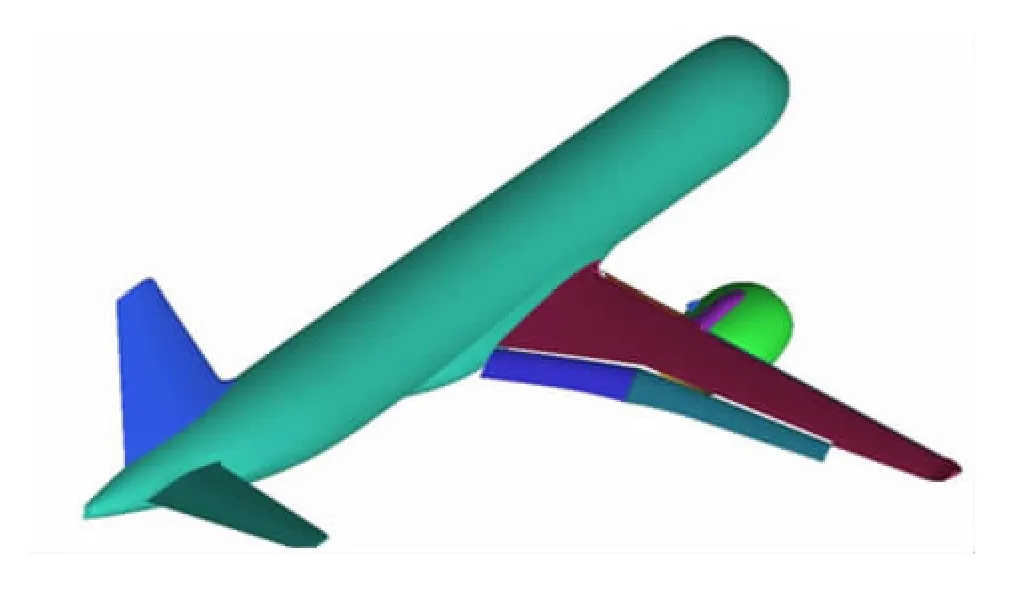
图2 某民机着陆构型几何示意图Fig.2 Sketch map of landing configuration of a civil aircraft

计算网格的拓扑设计与网格点分布应符合增升构型的流场结构和流动特性，图3、图4分别为Trapwing半展构型和该民机构型的网格拓扑和物面网格点分布图，计算网格规模分别为15 726 144网格点和32 281 538网格点。

图3 Trapwing物面网格分布Fig.3 Surface mesh of Trapwing model

图4 某民机着陆构型物面网格分布Fig.4 Surface mesh of landing configure of a civil aircraft

2.2 雷诺数对气动力系数影响

2.2.1 Trapwing模型气动力分析

计算状态:Ma=0.15，α =0°～24°，Re=3.5×106，6.0 × 106，9.0 × 106，1.2 × 107，1.5 × 107，2.0×107。

图5为不同雷诺数状态下的升力系数与阻力系数曲线的对比。可以看出，CFD结果预测升力线斜率与试验数据吻合很好，低雷诺数下的升力系数比试验数据稍大一些，阻力系数曲线显示计算结果与试验数据吻合很好。图5还表明，小迎角下雷诺数效应对升力和阻力系数的影响较小，随着迎角的增加，雷诺数效应的影响增大。

图6为α=23.455°状态的升力系数和阻力系数曲线。可以看出，随雷诺数的增大，CFD和风洞试验预测的升阻力增大，当雷诺数增大到1.5×107时，升力系数出现小幅减小，其后随雷诺数增大而平缓增大。

图 7 为 Re=3.8 ×106，α =8°，20°，28°，32°状态下，翼尖部分的风洞荧光丝线试验与CFD结果的流线分布比较。可以看出，CFD结果与风洞试验结果预测的流动分离一致。从图7还可以看出，在8°迎角时，CFD结果预测到了从翼尖向内0.2倍展长的范围内的气流分离;随着迎角增大，分离区域逐渐增大，当迎角达到32°时，外翼段气流几乎完全分离，产生了逆风流场。

图5 Trapwing模型的升力系数和阻力系数Fig.5 Lift coefficient and drag coefficient of Trapwing model

图6 升力系数和阻力系数随雷诺数的变化Fig.6 Lift coefficient and drag coefficient with the increase of Reynolds number

图7 翼尖流动特性的CFD与风洞试验结果比较Fig.7 Comparison of wingtip flow characteristic between CFD results and wind tunnel test results

2.2.2 某民机着陆构型计算分析

计算雷诺数范围:Re=1.75×106，2.8×106，5.2 ×106，6.0 ×106，6.9 × 106，9.0 × 106，1.2 × 107，1.5 ×107，2.0 ×107。图 8 为迎角分别为 12°和 16°状态下升力系数和俯仰力矩系数随雷诺数变化的趋势。可以看出，与Trapwing构型类似，升力系数随雷诺数的增加而增大，俯仰力矩系数随雷诺数的增加而减小;1.75×106～6.0×106雷诺数范围内，气动力和力矩系数对雷诺数变化十分敏感;6.9×106以上，气动力和力矩系数趋于平缓。

图8 升力系数和俯仰力矩系数随雷诺数的变化Fig.8 Variation of lift coefficient and pitching moment coefficient with the increase of Reynolds number

2.3 雷诺数对转捩位置的影响

图9 Trapwing机翼雷诺数对压力分布的影响Fig.9 Reynolds number of Trapwing influence on pressure distribution

为进一步研究雷诺数对增升构型气动特性的影响，从流动特性入手，分析雷诺数对增升构型边界层转捩和流动分离的影响。图9为α=23.455°Trapwing增升机翼在不同雷诺数下机翼弦长随压力分布的变化情况。可以看出，雷诺数3.8×106状态下，缝翼、襟翼边界层转捩位置靠后;随着雷诺数增大，转捩位置前移;雷诺数继续增大到9.0×106及以上，流动的粘性效应减小，缝翼上表面的层流区消失，襟翼上的转捩位置基本不再发生变化。

图10 Trapwing机翼不同雷诺数下流线分布Fig.10 Streamline distribution of Trapwing with different Reynolds number

图10 为α=23.455°下Trapwing增升机翼上表面的流线分布，显示了不同雷诺数状态的层流边界层区域变化情况。

2.4 雷诺数对流动分离的影响

图11给出了某民机α=18°下雷诺数对外襟翼和翼尖位置上流动分离的影响。可以看出，随着雷诺数增大，襟翼分离位置向后缘移动，雷诺数达到6.9×106以上时，分离位置和分离区域趋于稳定。

图12为α=18°下雷诺数对机翼表面压力分布的影响。由左侧图可以看出，随雷诺数增大，缝翼和主翼前缘的吸力峰值增大，雷诺数大于6.9×106时压力分布的变化不太明显。右侧图显示，雷诺数对压力分布影响主要体现在外襟翼上，压力分布显示外襟翼上存在流动分离，且分离位置随雷诺数增大向后缘移动。

图12 着陆构型雷诺数对表面压力分布的影响Fig.12 Influence of landing configuration Reynolds number on pressure distribution

3 结论

本文采用CFD方法模拟了增升装置不同雷诺数状态下的低速流场，分析了雷诺数对气动力、流动分离、边界层转捩的影响和规律，研究结果表明:

(1)随雷诺数增大，升力系数和最大升力逐渐增大，力矩系数变小。气动力和力矩系数在小于6.9×106表现为雷诺数影响敏感区;低雷诺数与高雷诺数升力系数差异约5.0% ～6.5%，力矩系数雷诺数效应更为明显。

(2)受雷诺数影响的物面流动分离区域主要位于外襟翼和翼尖后缘区;随雷诺数的增加，外襟翼上流动分离位置向后缘移动，而边界层转捩位置向前缘移动。

(3)雷诺数大于6.9×106时，缝翼和主翼上压力分布受雷诺数影响不太明显;雷诺数1.75×106状态下的物面压力分布与其他雷诺数下的差异较大，该状态下的气动数据需谨慎应用。

［1］ Mitsuhiro Murayama，Yuzuru Yokokawa.Numerical simulation of half-span aircraft model with high-lift devices in wind tunnel［R］.AIAA-2008-0333，2008.

［2］ Pettersson Karl，Rizzi Arthur.Aerodynamic scaling to free flight conditions:past and present［J］.Progress in Aerospace Sciences，2008，44(2):295-313.

［3］ Rudnik R，Germain E.Reynolds number scaling effects on the European high-lift project configurations［J］.Journal of Aircraft，2009，46(4):1140-1152.

［4］ Rudnik R.Stall behaviour of the EUROLIFT high lift configurations［R］.AIAA-2008-0836，2008.

［5］ Johnson PL，Jones K M，Madson M D.Experimental investigation of a simplified 3D high lift configuration in support of CFD validation［R］.AIAA-2000-4217，2000.