地磁姿态探测器的实时标定方法研究
杨宇彬,汤国建,包为民
(1.国防科学技术大学航天科学与工程学院,湖南长沙410073;2.四川航天系统工程研究所,四川成都610100;3.中国航天科技集团公司科技委,北京100830)
0 引言
地磁场是地球固有物理矢量场,具有稳定、隐蔽、难以人为干扰的特性。自从1989年美国Cornell大学Psiaki等人率先提出利用地磁场确定卫星轨道概念以来,这一方向逐渐发展成为国际导航领域的研究热点,所衍生出的地磁导航、地磁制导与地磁姿态探测是航空、航天领域重要的研究方向。
地磁测量具有无辐射、全天时、全天候、全地域的特征,与其他有源制导、导航或探测方式相比,地磁测量在军事领域有着无可比拟的优势。使用地磁制导的导弹抗干扰性能强、突防能力强,俄罗斯新型机动变轨的SS-19导弹采用地磁等高线制导系统,实现了导弹的变轨制导[1],以对抗美国的反弹道导弹拦截系统。SS-19导弹再入大气层后,不按抛物线飞行,而是沿地磁等高线飞行,使美国导弹防御系统无法准确预测导弹的飞行轨迹,增强了导弹的突防能力。法国正在研究一种全新的以地磁测量为基础的炮弹制导系统。德国则研究了基于卡尔曼滤波的地磁导航系统,应用于导弹并成功试射。近年来,国内工业界和学术界也十分重视地磁姿态测量、地磁导航的应用研究。由于地磁测量的成本低、无辐射、隐蔽性好、全天候、抗冲击振动特性好,特别适合用于导弹实时姿态探测。但是,工程实用尚需解决地磁测量易受铁磁性物质或其他设备引起的磁场畸变影响、温度漂移、强磁干扰等问题,磁差标定与补偿是工程应用的研究重点。
本文针对当前普遍采用的磁差标定方法不适用于导弹飞行环境的工程问题,提出了一种实时磁差标定与补偿方法。
1 地磁场模型
地磁场具有磁位特征,即:

式中,B为地磁场强度矢量;U为地磁场磁位。通常采用当地地理坐标系OxTyTzT来描述磁场强度分量,可以得到沿坐标轴xT,yT,zT三个方向磁场强度的分量为:
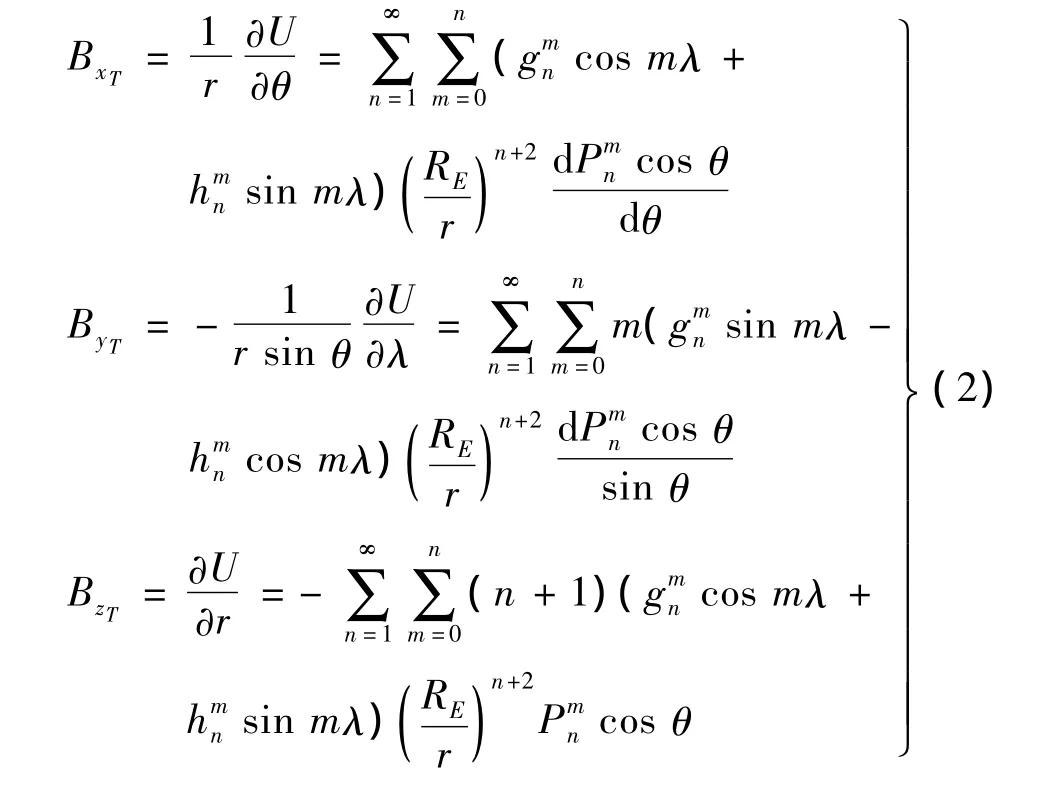
式中,r为空间一点距地心的距离;RE为地球平均半径;λ为格林尼治起算的东经;θ为余纬;为n次m阶Lefendre函数为基本磁场的高斯系数。实测表明,采用国际参照地磁场(IGRF)模型即具有满意的精度。
2 磁传感器静态磁差标定方法
2.1 工作原理
磁阻传感器是利用合金电阻对某一个方向磁场敏感的原理制成。由于磁传感器体积小且没有活动部件,功耗很低,配合选用体积小、功耗低的外围器件,可以将探测器微型化,已经有逐步取代磁通门的趋势,因此,非常适合导弹、火箭等飞行器使用。
2.2 静态磁差标定
磁传感器因制造和环境影响,测量时会产生误差,一般分安装误差、零偏、刻度因子误差和非正交误差。因此,实际应用需对磁传感器的误差进行补偿。
基于补偿精度和工程可实现性要求,建立如下磁传感器输出模型:
式中,Uhx,Uhy,Uhz为磁传感器的输出;Uhx0,Uhy0,Uhz0为磁传感器零位;Kx,Ky,Kz为磁传感器标度因数;Hx,Hy,Hz为磁传感器输入的激励磁场强度;Kxy,Kxz,Kyx,Kyz,Kzx,Kzy为磁传感器的安装误差系数。
静态磁差标定可基于位置试验对模型中的参数进行辨识,采用12位置标定方法来确定磁传感器模型中的系数[2]。静态磁差标定通常在产品交付前由研制厂家完成,标定系数烧写在弹载计算机内置的Flash芯片内。
3 磁传感器实时动态标定算法
3.1 椭圆拟合标定算法
现有的标定方法分三步依据磁传感器的输出辨识标定系数[3],补偿温度引起的零偏、灵敏度漂移、导弹自身铁磁干扰以及其他异常磁干扰引起磁场畸变导致的影响。算法步骤如下[4]:
(1)确定旋转因子
图1为椭圆旋转示意图。首先将椭圆旋转δ角度,此时椭圆长轴由原来的r转到r'的位置。取长短轴平方和的最大值,令
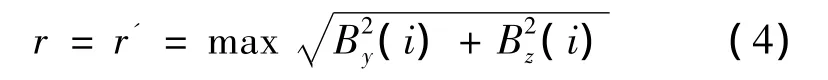
可得此时转角δ有如下关系式:

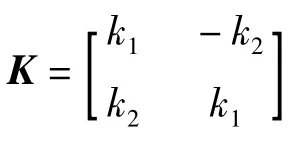
(2)确定伸缩因子,将椭圆修正成圆
在使用环境中,磁传感器输出数据经第一步旋转后,记录Y,Z轴的最大值和最小值,通过伸缩变换,将椭圆修正成圆,伸缩因子为:
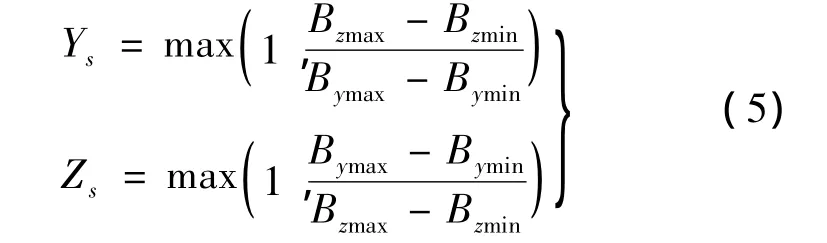
(3)平移因子,将圆心与坐标原点重合
经旋转和伸缩后的地磁数据圆心并不与坐标原点重合,需进行平移,平移因子为:
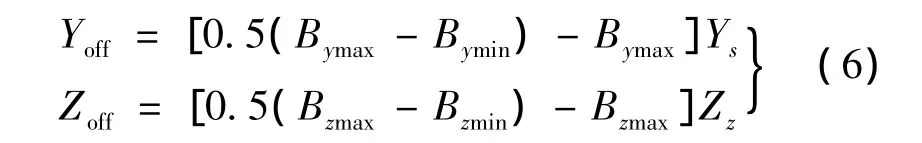
该算法在试验室条件下被证实是有效的,但首次应用于某项目飞行试验中未获得满意的结果。事后分析表明,由于该项目导弹执行机构采用了电磁阀驱动舵机动作,电磁阀工作瞬间产生的强磁脉冲信号叠加了磁干扰,该异常磁信号未被硬件滤波器以及FIR软件滤波器滤除,而直接用于实时动态标定,导致标定失效,滚转姿态测量失效。为解决该工程实际问题,必须研究专用的异常磁信号滤除算法。

图1 椭圆旋转补偿法Fig.1 Method of the ellipse rotation compensation
3.2 异常磁信号滤除算法
本文提出的异常磁信号滤除算法的思路是:首先使用白噪声多项式最优线性移动平滑算法对磁采样数据进行预处理,通过预测下一采样时刻传感器的输出滤除可能出现的野值,滤除异常信号的采样序列可用于3.1节描述的标定算法。
按移动平滑的基本思想,在连续采样的数个毫秒内,传感器的输出x(i)总能用一个时间变量的p阶多项式描述,假设磁传感器的输出为:

式中,P(i)为p阶多项式;ε(i)为白噪声序列。
用一组时间函数的多项式族{pj(i),j=0,1,…,p}的线性组合来表示P(i),可简化多项式计算过程,即 ,其中 θj为系数。将式(7)写为矩阵形式X=Pθ+ε,其中:

式中,N为窗口宽度,则:

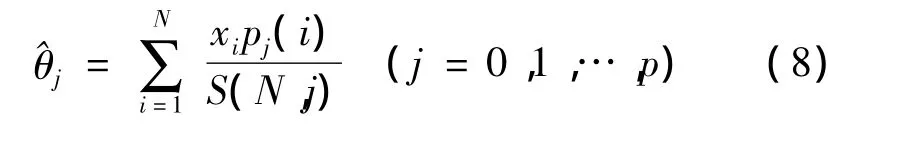
由式(7)得到拟合曲线:

计算^x(i)在N+a处的零阶微商的最优线性无偏估计,得:

即权系数的无偏最优估计为:
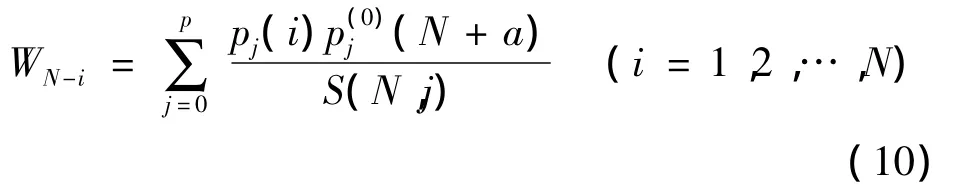
式中,a为滤波位置点。当a=l时定义为l步预测算法;a=0时为滤波算法;a=-(N-1)/2时为中心平滑算法。本文取a=l=1进行一步预测。显然,一旦确定了“窗口”宽度N和模型阶数p,则预测算法的权系数也随之确定。记序列{x(n-N+1),…,x(n)}对x(n+1)的预测为 ^xn|n+1,有:

具体操作中,首先可从飞行试验遥测数据中取出连续的N个磁数据进行p阶多项式拟合,通过试算和全局要求确定参数N和p的具体值,由式(10)计算出 N 个权系数 WN-i(i=1,2,…,N);然后将这些权系数作为一个“窗口”存储在弹载计算机中,对于观测数据序列只需由式(11)计算一步预测值。该算法为一种动态预测方法,当后继测量xn+1满足时,判定xn+1为野值,用预测值代替,其中μ为判别阈,需根据实际情况选择,阈值取得过小会引起误判。实际使用时取为离线辨识的幅值参数,m的取值由采样频率和导弹的弹道特性确定。
3.3 标定补偿算法对比验证情况
通过地面转台和飞行试验验证异常磁信号滤除算法以及标定算法的效果。
3.3.1 转台验证
转台试验中,导弹执行机构的电磁铁按设计频率工作。未采用异常磁数据滤除算法时,计算的滚转角与转台码盘角度对比如图2所示,可见显著跳动。采用异常磁数据滤除算法后,标定并补偿的磁数据如图3所示,计算的滚转角与码盘角度对比如图4所示。可以看出,计算的滚转角与转台码盘角度一致性好,可见野值滤除算法的效果明显。采用本文提出的异常磁数据滤除算法后,标定、补偿的精度显著提高,不同转速情况下的滚转角测量误差总小于1°,满足工程应用需要,详见表1。

图2 滚转角对比图Fig.2 Comparison of roll angle
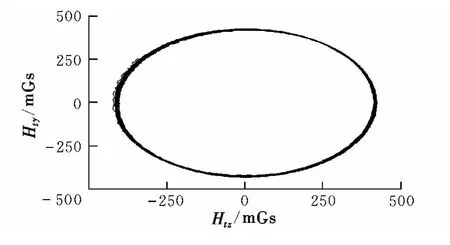
图3 补偿后的地磁信号Fig.3 Geomagnetic signals after compensation

图4 补偿后的滚转角对比图Fig.4 Comparison of roll angle after compensation

表1 不同转速下滚转角测量误差 (°)Table 1 Roll angle error of different revolutions
3.3.2 飞行试验验证
导弹飞行试验采用本文提出的磁数据预处理与标定算法,结果表明算法能可靠滤除执行机构动作引起的磁信号野值,详见图5;弹上计算机实时解算的滚转角见图6,经实时标定补偿后,磁解算滚转角线性度有所提高。
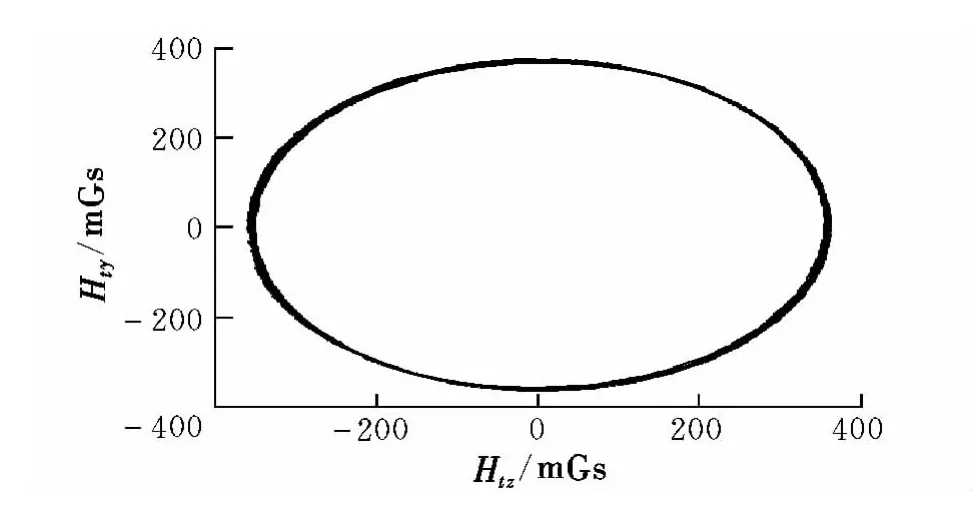
图5 飞行中标定后的磁信号Fig.5 Magnetic signals after in-flight calibration

图6 飞行中标定补偿后的滚转角Fig.6 Roll angle after in-flight calibration compensation
实测表明,进行一次实时标定耗时约0.7 ms,而计算周期为1 ms,即在一个计算周期内能实现快速标定,并将标定结果用于补偿下一计算周期磁采样数据;磁采样到来时,标定与补偿递推进行,实时性满足某转速高达10 r/s的导弹制导控制的要求。
4 结束语
本文提出的实时磁差标定与补偿方法重点解决了异常磁信号野值滤除问题。该方法经转台试验与飞行试验验证,具有鲁棒性优、精度高、实时性好的特点,解决了传统磁差标定方法获取的补偿系数不适用于某型号高速滚转导弹姿态探测的问题,具有工程应用价值。
[1] 李素敏.地磁场资源在匹配制导中的应用研究[J].制导与引信,2004,(3):19-21.
[2] 张娇,陈静,杨栓虎.三轴磁阻式传感器标定方法研究[J].弹箭与制导学报,2010,30(6):46-48.
[3] 邵婷婷,马建仓,胡士峰,等.电子罗盘的倾斜及罗差补偿算法研究[J].传感技术学报,2007,20(6):1335-1337.
[4] 史连艳,宋文渊,王红云.基于旋转因子的磁传感器误差补偿改进椭圆法[J].探测与控制学报,2010,32(2):5-8.

