舰载机航空保障需求及排队网络模型研究

吕开东，朱齐丹，李新飞

(1.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001;2.哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨150001)

0 引言

舰载机航空保障活动所涉及的内容纷繁复杂，在执行出航作战任务过程中，对舰载机的保障任务进行科学规划和决策尤为重要。本文针对舰载机航空保障调度的全过程、空间范围、保障活动和资源规划等方面对舰载机航空保障组成进行分析，同时对保障人员的配备、保障装备的配置、航空弹药的需求等进行研究，建立数学模型，有效调度舰载机及其各航空保障资源，使舰载机在正确的时间得到准确的保障，进而缩短舰载机航空保障时间，提高航空保障的效率。

1 舰载机航空保障需求分析

舰载机航空保障是受舰载机类型及其执行任务类型和武器适配性要求、甲板作业空间、设备配置方式和性能、人员匹配状况和任务适应性、维修保障力量需求等众多因素制约和影响的多任务复杂问题［1］。

1.1 作战任务需要分析

航母作战指挥系统按照作战任务规划下达舰载机应战指令，根据作战任务需要确定舰载机的出动方式。不同的出动方式需要调动的飞机类型和数量不同，所需的航空保障内容和方式也各有不同。舰载机出动离舰执行任务，首先需要确定舰载机的出动方式，然后由此确定保障机制。目前，美国航母舰载机根据作战任务的需要所采取的出动方式主要有单波作业方式和连续作业方式两种。单波作业方式适用于攻击性的防空作战、对海对岸攻击及两栖作战火力支援等集中攻击的作战活动，这也是大多数航母在海战中所采用的出动方式。而连续作业出动方式虽能延长在空中的作战时间且能执行多种作战任务，但却因两飞行周期交替重叠相互制约，一般用于航渡、待机、护航等防御性的作战活动。两种出动方式对航空保障内容的需求基本相同，但保障过程和所需要的资源却有一定的差异。所以，在进行作战任务规划时，就要分别在两种作业模式下考虑舰载机的航空保障策略问题。

1.2 航母空间因素分析

舰载机在航母上的作业空间涉及飞行甲板、机库、升降机三个部分。飞行甲板是舰载机在航母上活动的主要空间，要为舰载机的起降、调运、布列、补给、维护等航空保障活动提供充分的作业空间，各个作业活动受甲板上的弹射系统、升降机系统、阻拦系统、保障设施等影响相当严重，故对飞行甲板作业区域的合理规划是非常重要和必要的。其次是机库区域的规划，不仅要考虑能够存放一定数量的舰载机，而且要充分考虑在保障设备、消防设施等相互妨碍的情况下，能够灵活、快速地实现对舰载机的调运，输送到升降机平台。升降机是舰载机往返于航母甲板与机库之间的运输通道，升降机台面的形状、大小、载运飞机的摆放形式，以及相关保障作业空间需求，都是影响舰载机航空保障顺利实现的重要因素［2-4］。

1.3 航空弹药需求分析

目前，在实施空中作战过程中，在空中只能进行燃油的补给作业，而弹药、氮氧气等则无法得到补给。舰载机要保持持续有力的打击力量，就需要不断地返回航母甲板进行弹药等的保障与补给，然后再升空继续加入战斗。不同的舰载机种所需要的航空弹药种类是不同的，不同的作战任务所需要的弹药类型和数量也不同［5-6］。所以，不仅要对舰载机挂载何种航空弹药、挂载多少才能满足作战需求进行分析研究，而且也要对各类航空保障任务和航空弹药的消耗规律进行分析研究。

1.4 航空保障人力资源配置影响分析

航空保障人员是航空保障的实施者，是航空保障人力资源的重要组成部分。由于接受保障的机种、需要保障机务类型、航空弹药需求等的多样性，不同保障活动所依赖的保障人员的技术和技术程度要求则有所不同，同样，不同专业和不同技术级别的保障人员对不同保障作业活动的工作效率也不一样。为了满足作战需求、保持舰载机战备完好性和保障性，需要对航空保障人力资源进行优化配置。通过对人力资源的专业知识结构、技术能力水平、工作胜任程度等因素进行优化配置，达到在保障人力资源耗费最小的前提下，使保障人员的数量恰好满足保障任务的需求，从而避免保障人力资源不必要的浪费［7］。

1.5 保障装备/设施配置影响分析

在对舰载机实施航空保障过程中，需要对舰载机或航空弹药配备相应的保障装备/设施，以辅助航空保障人员完成各种保障任务，如舰载机故障检测装置、转运牵引拖车、加油装置、弹药运输等。由于舰载机挂载的航空弹药类别和数量的差异，需要配套的保障装备/设备也存在差异，而且，目前大多数航空弹药的保障装备/设施的发展相对滞后于弹药本身的发展。因此，在改进和加强航空保障装备/设施研制的同时更要加强对舰载机航空保障、弹药保障及其保障装备/设备进行合理优化和匹配，提高航空弹药保障的效益和质量，提升航空保障能力。

除上述情形外，航空保障的效率和质量还要受到飞机升降机和弹药升降机的提升和复位速度、喷气偏流板的起降速度和降温时间、牵引拖车的工作效率、挂弹和加油效率等诸多因素的影响［8］。

2 舰载机舰面航空保障排队网络模型

舰载机航空保障任务繁多、过程复杂、涉及因素众多。为了简化问题，仅就舰载机在飞行甲板上进行舰面航空保障的过程建立排队网络模型。

2.1 前提和假设

对于舰面航空保障过程，由于航母舰面空间的限制，飞行甲板的弹射起飞区、回收阻拦区、停机区、加油区、武器挂载区和维修保障区等造成各功能区域重叠交错，从而影响航空保障作业效率。故按舰载机准备出动接受保障服务的顺序划分为:预检维护站位、机务站位、挂弹站位、过渡站位、弹射站位、空中飞行和着舰回收等。除舰载机被弹射起飞直至着舰回收后自动运行至预检维护站位以外，其他两两站位之间舰载机都需要拖车牵引服务，所以，将两站位间的牵引过程视为服务台工作过程。在此前提下进一步假设如下:

(1)假设舰载机在单波出动模式下执行攻击性作战任务，且一次作战任务中所有飞机采用同一种挂载方案;

(2)只考虑固定翼战斗攻击机(F/A-18E/F“超级大黄蜂”)的航空保障问题，不考虑直升机等其他机种;

(3)不考虑舰载机起飞后执行任务的过程。

2.2 建立舰载机航空保障系统排队网络模型

J.R.Jackson在20世纪五、六十年代最先开始研究排队网络，而且是以开环排队网络为研究对象的，所以开环排队网络常被称为Jackson网络［9］，其状态集为:

式中，li表示第i个服务点的队长。

2.2.1 开环排队网络模型描述

舰载机舰面航空保障系统的运行过程如图1(a)所示，它是一个多排队串行工作的排队网络系统。在作业过程中，每波次飞机着舰回收过程可视为服从外部顾客的泊松输入，舰载机作为接受服务的顾客依次要在多个(6个)服务点被服务，而在某一服务点内又有多个相同的服务台，然后弹射离开系统，顾客流被输出到外部。基于上述特征，恰好可以建立一个舰载机航空保障系统的开环排队网络模型，如图1(b)所示。

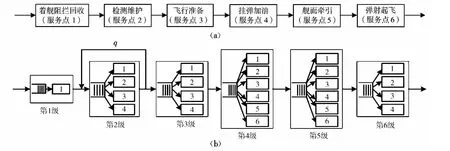
图1 航空保障开环排队网络模型Fig.1 A network model of open loop queuing for aviation security

(1)服务点M=6个，假定各服务点服务时间相互独立并服从负指数分布。其中第1级服务点为着舰回收排队系统，假定飞机到达服从参数为λ1的泊松过程，服务窗口只有1个，同一时间段只能服务1架飞机，服务速率为μ1;第2级服务点为检测维护排队系统，此服务点分为4个服务窗并行服务，各服务窗服务速率为μ2;第3级服务点为飞行准备阶段的机务保障排队系统，有4个服务窗，各服务窗服务速率为μ3;第4级服务点为弹药挂载排队服务系统，设有6个服务窗，各服务窗服务速率为μ4;第5级服务点是飞机站位间的调运排队系统，假定舰面上的调运工作都集中在一个服务节点，设有6个保障小组，6个服务窗，服务速率同为μ5;第6级服务点为飞机弹射站位的排队系统，设有4个服务窗，且具有相同的服务速率μ6。

(2)任意一个服务点的顾客(飞机)都是来自于上一服务点，而被服务完都进入下一服务点，即任一服务点间的转移概率均为pij=1，且与历史无关。在第2级系统中，一般会有5%的可能飞机出现故障而离开系统，但是可以随时从备用飞机中调度来替换它，则此时输出和输入为相等概率q的飞机，构成一带有反馈的排队系统。

(3)排队系统是开环网络，顾客从系统外部到达系统内任何节点的外部输入都是泊松到达过程，且顾客源是无限的。

(4)排队规则遵循等待制，服务规则遵循先到先服务的原则。

2.2.2 排队网络模型性能分析

如用N(t)表示t时刻网络系统的状态，因N(t)来自于有限向量集S，其状态空间中任何状态之间都是相通的，各个服务点的顾客队长是相互独立的，很容易判断N(t)是一个不可约的、非周期的马尔可夫链，则这个排队系统是遍历的，其必存在平稳状态。根据 Jackson定理，开环排队网络满足以下条件:

(1)顾客从网络外部到达第i个服务点的事件流为λi的泊松流;

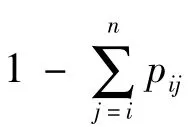
(3)若将第i服务点的外部到达率λi和从其他节点到达i服务点的所有到达率之和设为第i服务点总的平均到达率为Λi，则满足方程组:

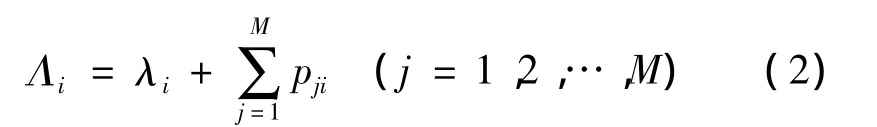
(4)若设第i个服务点有li个顾客，即系统的状态为 S=(l1，l2，…，lM)，则在统计平衡条件下系统的概率满足:

式中，pi(li)为平衡条件下第i个服务点有li个顾客的概率。

(5)开环排队网络中每个节点都可以独立地使用M/M/1或M/M/n模型进行分析，证明过程见文献［10］。

故求解开环排队网络模型按以下两步进行:第1步:求解各个服务节点的顾客平均到达率和服务率;

第2步:分别求解稳态下各服务节点的目标参量。

(1)系统平均队长:

(2)平均排队队长:

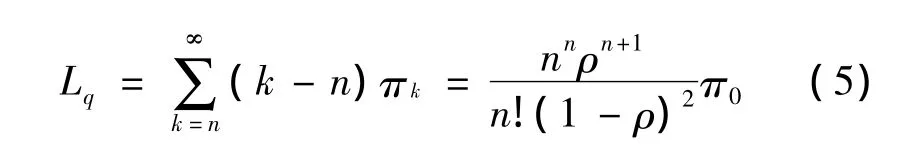
(3)平均停留时间:

(4)平均排队时间:

2.3 舰面航空保障的开环排队网络计算

2.3.1 求解各服务节点的平均到达率和服务率

在排队系统的第1级排队系统中，输入即为外部输入，即λ1=λ;

第2级排队系统中，输入为:

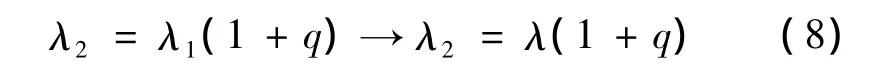
在第3级系统中，输入为:

其他各级系统的输入不变，则都与λ3一致。舰载机航空保障系统各服务节点的输入率、服务率、服务窗数详见表1。

2.3.2 求解各服务节点的目标参量

分别求得稳态下各服务节点的目标参量，如表2所示。

表1 舰载机航空保障系统的参数Table 1 Parameters of aviation security system

表2 舰载机航空保障系统的目标参量Table 2 Target parameters of aviation security system

2.4 计算结果分析

按照美国航母编队的常规操作规范，飞行甲板作业周期如表3所示。对比表中数据，本文在4部弹射器全部使用情况下所计算的甲板停留时长为37.49 min，则对应的飞行甲板作业周期应当选择为1+30周期。分别就弹射器数量为1，2，3情况进行计算时，得到了网络系统平均队长分别为17.35，18.13，18.87;对应平均停留时间分别为34.77 min，36.33 min，37.82 min。则当使用 1 部弹射器时选择1+15周期比较适当;对于使用2或3部弹射器工作时，选择1+30周期的工作强度都比较低，可以考虑调整排队网络中间各排队服务环节使整个系统匹配到更优状态。从分析过程看，在第3个服务节点上飞行准备阶段的平均排队队长达到5.02，可以通过增加服务窗口调节系统状态。

表3 舰载飞机飞行甲板作业周期Table 3 Time of aircraft flight deck operation

3 结束语

在对舰载机类型、执行任务类别和武器适配性要求、甲板作业情况、设备配置方式和性能、人员匹配状况和任务适应性、维修保障力量需求等众多因素进行分析的基础上，通过舰载机航空保障的排队网络模型验证了应用排队理论进行舰载机航空保障过程分析的可能性，并且可以得到相关的数据信息，为解决舰载机航空保障系统的复杂问题提供了理论参考。

［1］ 魏昌全，陈春良.基于出动方式的舰载机航空保障调度模型［J］.海军航空工程学院学报，2012，27(1):111-114.

［2］ 司维超，韩维，史玮韦.基于POSS算法的舰载机舰面布放调度算法研究［J］.航空学报，2012，33(11):2048-2056.

［3］ 刘钦辉，邱长华，王能健.考虑空间约束的舰载机作业调度模型研究［J］.哈尔滨工程大学学报，2012，33(11):1435-1439.

［4］ 林华，占明锋，周丰.舰载机回收任务的优化调度算法及仿真［J］.海军工程大学学报，2008，32(1):50-54.

［5］ 韩维，商兴华，李成.舰载机维修保障力量需求研究［J］.海军航空工程学院学报，2010，25(6):670-674.

［6］ 吕晓峰，郭小威，王云飞.基于遗传算法的舰载机弹药调度次序［J］.兵工自动化，2011，30(8):10-12.

［7］ 陈新，辛文逵，虞健飞.从美伊战争看航空维修保障高新技术［J］.航空维修与工程，2003，(3):48-50.

［8］ 王兵.对舰载机出动能力的认识［J］.现代舰船，2012，(11):40-43.

［9］ 史宪铭，郭波，武小悦，等.基于排队网络的快速研制系统模型研究［J］.系统工程学报，2007，22(6):654-658.

［10］ 胡奇英.随机运筹学［M］.北京:清华大学出版社，2012:12-60.