大气紊流建模与仿真

王化东

(中国人民解放军93818部队，北京100843)

0 引言

一般情况下，飞行模拟所建立的环境都是以平静大气为主，并未考虑到大气扰动对于飞机飞行的影响。但是实际上真实的大气中存在着各种各样的大气扰动，这些扰动对于飞行器的品质有非常大的影响。因此为了增加地面仿真的真实性，需建立与真实大气环境相似的大气扰动模型并应用于地面仿真。开展大气扰动建模技术的研究对于研究飞行器在扰动环境下的品质特性、提高仿真的逼真度有着非常重要的意义。

大气扰动包括很多种形式:低空的稳态风、大气紊流以及阵风。在这些气流扰动中大气紊流最为复杂，模型建立也最为困难。本文将基于Dryden模型针对大气紊流数学模型的仿真计算进行详细探讨［1］。

1 大气紊流数学模型

大气紊流现象的形成和出现一般与地形诱导、热交换、风切变等因素有很大的关系。同时飞机、舰船等拖曳的尾流也会形成紊流区，例如对于运动的舰船来说，在舰船的尾部区域也会形成一个紊流区，称之为舰尾流，它是由于甲板风流过舰船上的各种建筑物所形成的，它的出现对于舰载机的着舰过程有着非常大的影响。

实际的大气紊流是十分复杂的物理现象。为了使飞机响应问题的研究不至于过分复杂，在保证模型准确度的基础上可进行适当的假设。一般来说，大气紊流是一个随机函数，它与时间和位置有着紧密的关系，这种函数关系是基于大量的测量和统计数据来进行构建的。在航空工程应用中，可以假设:大气紊流的统计特征(即平均值和均方差，以及相关函数和频谱函数)既不随时间而变(认为紊流是平稳的)，也不随位置而变(认为紊流是均匀的)，在这种假设条件下可以满足对飞机品质特性分析的需要。

目前常用的大气紊流模型是德莱顿基于大量测量和统计数据提出的，其对应的指数型纵向相关函数为［2］:f(ξ)=e－ξ/L。基于测量和统计数据求得f(ξ)和g(ξ)后，然后对得到的结果通过 Fourier变换，可求出 Dryden模型的纵向和横向频谱函数如下:

这里

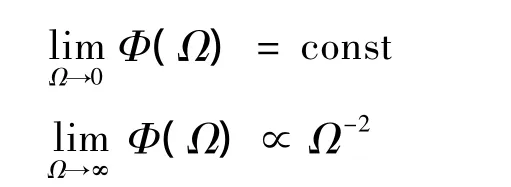
得到的频谱函数是基于“平稳”和“均匀”两个假设条件得到的，这就会使得所得到的这个模型在无穷远处的渐进性质是不符合实际紊流理论的，但这并不影响实际的工程应用。该Dryden模型的优点在于:相对来说频谱的形式较为简单，可以通过常规的数学方法进行处理，而这一点对于紊流数值仿真是非常必要的。

2 仿真计算理论

为了完成对大气紊流的仿真计算，针对上述求得的大气紊流频谱函数，设计如图1所示的仿真计算流程。

图1 生成大气扰流的仿真计算流程图Fig.1 Simulation calculation procedure for creating atmospheric turbulence

要生成大气紊流数据，需要解决的问题就是作为输入的随机信号的生成以及成型滤波器的设计计算。严格来说，在大气紊流的数值仿真过程中所要求的输入信号是真正的随机信号，但是在实际的数字计算机中，任何运算都是按一定的算法由相应的程序进行的，所以，不可能产生真正的随机数，只能产生“伪随机数”，其特征仅近似地符合白噪声。

通常情况下，所使用的数字计算机字长为32 bit。在数学上可以按如下公式生成在［0，231－1］之间均匀分布的随机数:

式中，初值r0可以任意选取;a和b为满足一定要求的奇数;mod为求余运算符号;m=231－1为最大整数。

图2为通过这种算法所得出的一段伪随机信号序列以及该随机信号的功率谱分析结果(其均值与方差分别为0.0383和1.0184)。

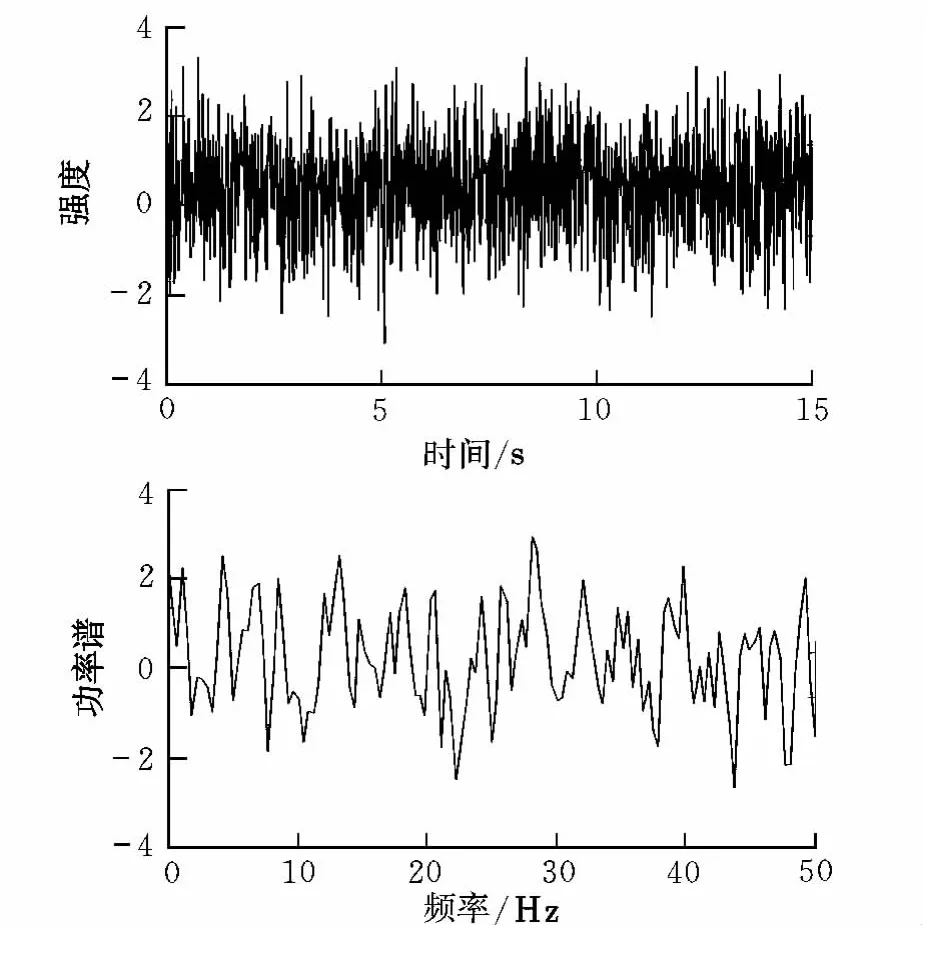
图2 程序计算生成的随机信号序列及其功率谱分析结果Fig.2 Results of random signal sequence and power spectrum analysis

要生成大气紊流数据，必须要使用成型滤波器进行计算，以伪随机信号作为输入，而且成型滤波器的设计必须依据于理论频谱函数，这样才能够保证所生成的大气紊流数据频谱特性的正确性［2］。成型滤波器就是通过滤波环节将白噪声转化为期望的有色噪声，如图3所示。

图3 成型滤波器Fig.3 Shaping filter

根据公式

可以得出:

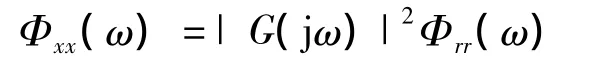
而白噪声的频谱为常值，令它为单位值，所以，输出的频谱为:

由此可见，只要把给定的输出频谱按照上式分解，就可以得到成型滤波器的传递函数G(s)。低空扰动模型使用的是Dryden紊流扰动模型，其空间域频谱表达式如下:

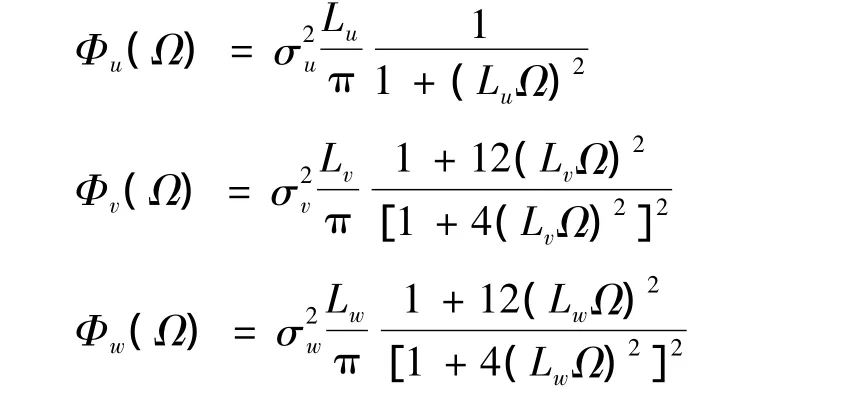
根据ω=ΩV(V为该方向上飞机的分速度)，可求得上述模型的时间域频谱表达式为:

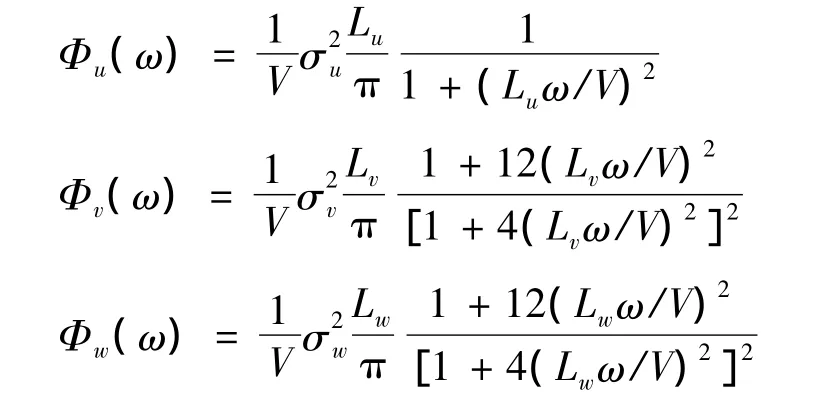
对上述各式进行分解，则可得到为了产生给定频谱Φx(ω)所需要的成型滤波器的传递函数Gx(s)。

对于3个分量，求出所需的传递函数如下:

以上所得到的就是可以进行大气紊流数值仿真计算所需要的成型滤波器所对应的传递函数的数学表达式。

对于成型滤波器的形式还不能直接在程序中运算，必须要由滤波器所对应的传递函数的形式得到可以在程序中以数值方法进行运算的递推公式，这也就是滤波器在程序中的实现方式。对于低空扰动的Dryden紊流扰动模型，则有如下递推公式:

3 仿真计算结果

根据上述所介绍的方法，可计算得到如下低空气流扰动模型的时间历程曲线，如图4所示。

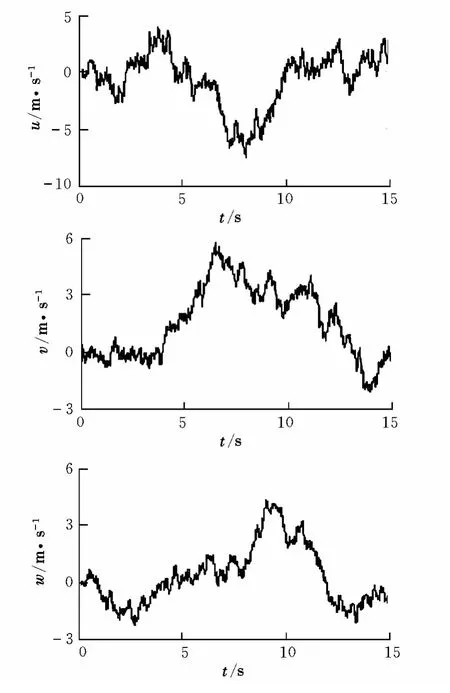
图4 低空扰动气流曲线Fig.4 Low altitude atmospheric turbulence

4 结果验证与修正

计算得到的大气紊流序列是否符合要求，要通过对生成的结果进行验证来体现。首先针对其中的伪随机序列的生成进行检验修正，由于上面得到的伪随机信号序列均值不等于零，标准偏差也不等于1，将该随机信号序列减去其均值再除以方差，可将随机信号序列的均值和方差修正为 －3.5009×10－17和1;然后就需要针对所生成的大气紊流序列进行检验了。其检验的准则就是要看由计算所得到的大气紊流序列xi(i=0，1，…，N)的频谱特性或者相关特性是否符合该紊流模型的频谱函数或者相关函数的理论表达式。对于这两种方法来说，检验相关函数是比较方便的。

按照定义，随机过程(大气紊流序列)x(t)的相关函数为:

对此式进行离散化，取τ=kh(h为步长，k为正整数)，于是就有

式中，相关函数的点数L不可太大，应该使L≪N。然后把由此得到的统计相关函数与理论相关函数画在同一幅图上，就可以衡量它们的吻合程度。

将低空大气紊流扰动模型空间频谱函数转化成时间频谱函数，再对上述的紊流频谱函数作Fourier逆变换，由此就可以得到相应的相关函数表达式。下面以u方向的大气紊流序列作为范例，未修正之前，所得到的u方向大气紊流序列如图5所示，其对应的相关序列可按照下式进行计算:

在该大气紊流序列中N=1500，可取L=50≪N。

对于低空扰动模型来说，采用的是Dryden紊流扰动模型，通过查表可知u方向上的尺度和强度分别为Lu=620 ft，σu=8.105(注:由于各种大气紊流模型中均以ft为单位，故在验证计算过程中采用英制单位，在最后结果中化为国际单位制)，因此在该方向上的紊流扰动模型为:

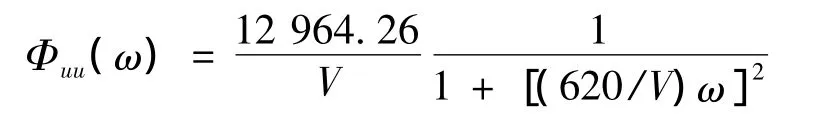
其对应的理论相关函数为:

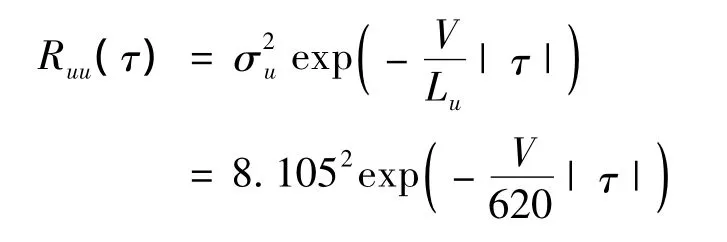
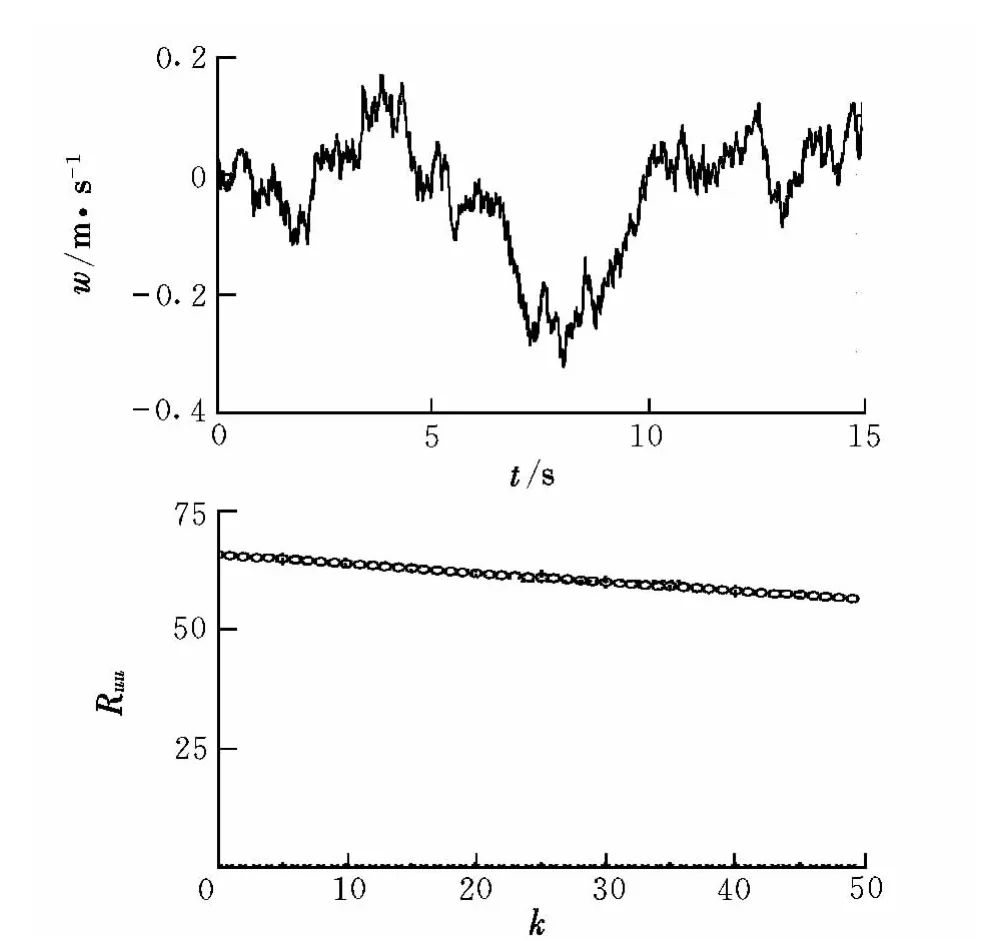
图5 修正前验证结果Fig.5 No fixed result

图5 中下图给出了实际生成的大气紊流相关函数曲线与理论频谱函数的相关函数曲线对比结果。图中，由“×”组成的曲线表示生成的大气紊流序列的相关函数曲线;由“·”组成的曲线表示理论频谱函数的相关函数曲线。由图中可以看出，不经过修正得出的结果与理论频谱的相关函数相差较大，计算结果远小于理论值，故需要对结果进行修正，修正的方法就是要对所得出的大气紊流序列的强度乘以一个修正系数，通过调整修正系数的大小，就可以使所得出的大气紊流序列的相关函数与理论频谱的相关函数基本吻合。修正后的大气紊流序列结果及验证结果如图6所示。

图6 修正后得到的验证结果Fig.6 Fixed results

图中，“·”和“×”分别表示理论频谱函数和所生成的大气紊流序列的相关函数。从图中可以看出，计算结果经过修正后与理论曲线的吻合程度还是比较令人满意的。

5 结束语

根据大气紊流的数学模型设计成型滤波器，并以白噪声信号为输入，能够得到大气紊流的仿真结果。但是利用相关函数验证后发现，此时所生成的大气紊流序列与原数学模型相差较大，不能直接用于仿真计算。通过适当的修正，能够得到比较准确的大气紊流序列，可用于各种地面模拟器以及空中飞行模拟器。

［1］ 朱华，黄辉宁，李永庆，等.随机信号分析［M］.第1版.北京:北京理工大学出版社，1990.

［2］ 肖业伦，金长江.大气扰动中的飞行原理［M］.第1版.北京:国防工业出版社，1993.