基于微分对策的导弹智能机动突防研究

鲜勇，田海鹏，王剑，史金倩

(1.第二炮兵工程大学7系，陕西西安710025;2.中国人民解放军96630部队，北京100025)

0 引言

随着不断地发展和试验，美国中段防御系统日趋成熟，其部署对我国导弹的中段飞行构成了重要威胁［1］。为提高导弹的作战效能，必须进行有效的突防。随着技术的不断创新，突防手段实现了多样化，其中弹头中段机动成为重要的突防手段。考虑弹头的有效载荷和机动过载限制，机动的时机和方向对弹头成功突防起着非常重要的作用。弹头中段飞行过程中，由美国防御系统释放的动能拦截器EKV(Exo-atmospheric Kinetic Vehicle)和弹头形成撞击-规避关系，可看成是“二人零和”博弈［2］问题。文献［3］基于微分对策对导弹中段突防进行了初步的研究，得出选择适当的时机机动可实现有效突防的结论。文献［4］用遗传算法求解冲量机动突防时机的突防方案，得出冲量机动在拦截末段最有效的结论。上述方法对分析弹头和EKV进行博弈的过程具有重要意义，但未对弹头全局的机动策略进行考虑。由于微分对策方法要求大量的计算，弹上的计算机无法满足要求，此方法尚未发展到实际应用的水平。

本文基于智能微分对策理论，建立了弹头与EKV对抗模型，将脱靶量和能量消耗作为EKV与弹头对抗指标，考虑弹头机动过载和控制变量的约束，建立了使用该方法的突防决策模型，并通过仿真验证了该方法的有效性。

1 弹头与EKV对抗模型

1.1 模型假设

为了便于研究，采用如下假设:

(1)弹头和EKV可视为质点;

(2)EKV末段拦截起点处于零控拦截状态［5］;

(3)EKV 的最大轨控加速度为4g［6］;

(4)EKV的速度为6～7 km/s;

(5)EKV捕获弹头时弹目距离为200 km［6］。

1.2 弹头运动状态方程

弹头进行中段飞行时仅考虑地球引力、柯氏及牵连惯性力。设发射系［7］下运动状态变量为m=［xm，ym，zm，vmx，vmy，vmz］T，加速度矢量为 um=［amx，amy，amz］T，则弹头在自由段的加速度为:

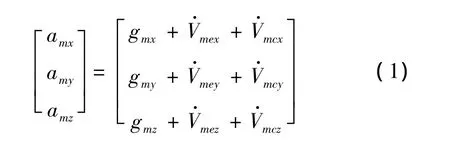
1.3 EKV运动状态模型

EKV运动状态方程和弹头相似，不同点在于加速度矢量不同。设EKV的加速度矢量为un=［anx，any，anz］T。EKV 采用扩展比例导引律，导引方程为［6，8］:

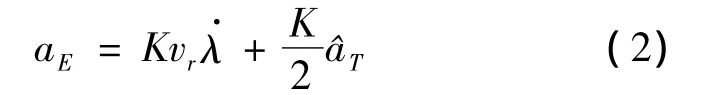
式中，K为比例导引系数;vr为EKV在弹头发射坐标系中的径向速度大小为视线角速度;为EKV对弹头加速度的估计。其中:

式中，θE，φE分别为EKV速度在其牵连坐标系中的俯仰角和偏航角;θL，φL分别为弹目视线在EKV牵连坐标系中的俯仰角和偏航角;TE为EKV的帧频。

根据模型需要，本文建立如图1所示的坐标系。图中，OeExeEyeEzeE为EKV牵连坐标系;O1Ex1Ey1Ez1E为EKV弹体系。

EKV 弹体系上的加速度为［0，aE］T，其中 aE=并且不超过 4g。则有:

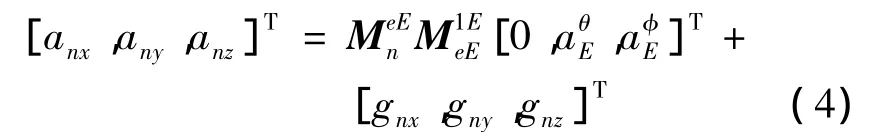
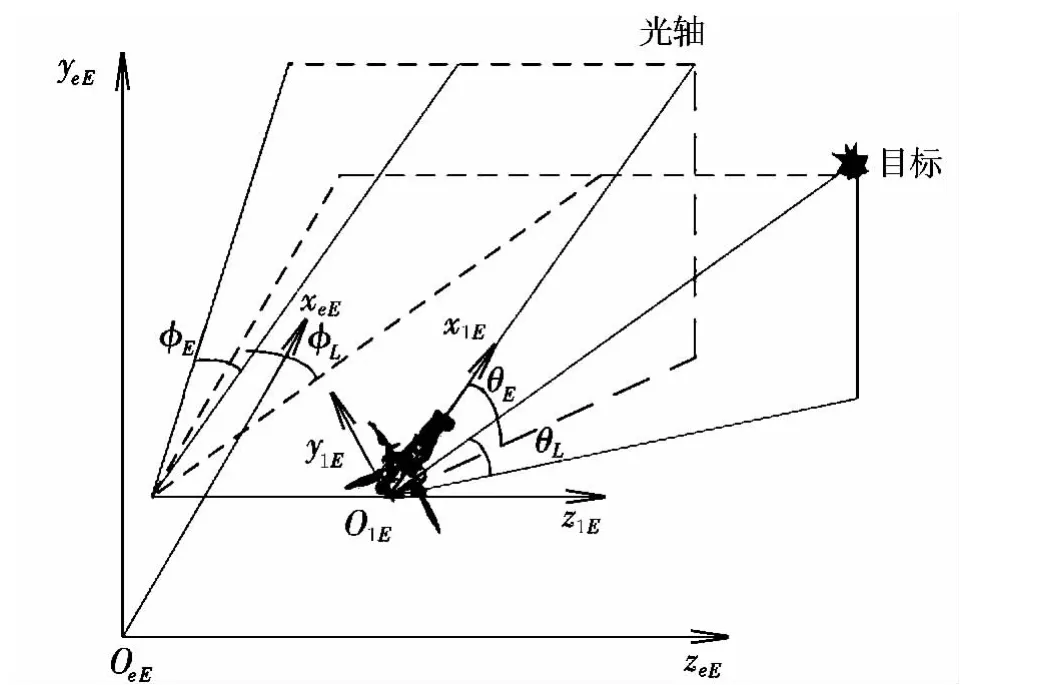
图1 EKV模型中的坐标系Fig.1 Coordinate system of the EKV model

2 机动方案设计

本文设计弹头借助双星预警系统［7］，在EKV捕获目标后(此时弹目距离小于200 km)，计算出EKV的位置和速度信息并传输给弹头。

2.1 机动策略

设弹头在质心位置处垂直于射面的正负两个方向各安装1个喷管，能产生2g的加速度。参照文献［8］得出的弹头进行发射系z轴负向机动时效果最好的结论，本文设计的弹头在进行机动突防时，垂直于发射坐标系Oxmym面机动，如图2所示。

图2 垂直发射坐标系Oxmym面机动Fig.2 Maneuver to the vertical Oxmym plane of the launch coordinate

2.2 试探性机动

由于EKV在捕获弹头时处于零控拦截状态，并且当弹头在EKV与弹头相距200 km机动时，在EKV的红外导引头上产生的横向视线角变化率最小，即此时的EKV探测弹头轨道变化的灵敏度较低，因此弹头向一个方向作一次持续的机动有利于扩大终端脱靶量。

本文设定EKV捕获弹头时的时间为t1，此时弹头开始垂直发射系Oxmym面负向机动，机动持续时间Δt。由于EKV末段拦截时间为17～20 s，所以弹头试探性机动时间不长，要为智能机动突防留下时间，可设 Δt=8 s。

3 微分对策数学模型

借助微分对策思想，将连续问题离散化，设拦截弹(E)、弹头(V)为对策双方，博弈的流程如图3所示。

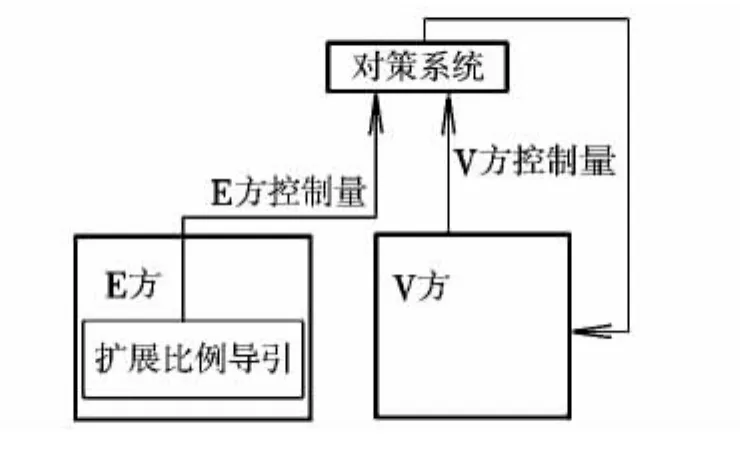
图3 拦截弹和弹头的博弈流程Fig.3 Game process of the interceptor missile and the warhead

系统的状态方程和初始状态为:

式中，x(k)为对策系统状态;u(k)，v(k)分别为V方和 E 方的控制变量，u(k)∈Uk=［－1，0，1］;u(k)=－1时弹头以2g的加速度垂直于发射系Oxmym面作负向机动;u(k)=0时弹头不作机动;u(k)=1时弹头以2g的加速度垂直发射系Oxmym面作正向机动。

系统以EKV的脱靶量和弹头实施机动所消耗的控制能量为考核目标，设代价函数为:

式中，θ(x(kf)，kf)为终端脱靶量;L(x(k)，u(k)，v(k)，k)= －u(k)2/400。

假设x(k)，u(k)分别为n维和m维列向量，b(k)为s维列向量，f，L，g是其所有变量的连续可微函数。集合Uk由不等式g(u(k)，k)≥b(k)，k=k0，k0+1，…，kf－ 1 给出，例如:gi(u(k)，k)=bi(k)=0。

最优控制问题是:求u(k)使u(k)∈Uk并使J最大。下面将最优控制问题化为非线性规划问题。设

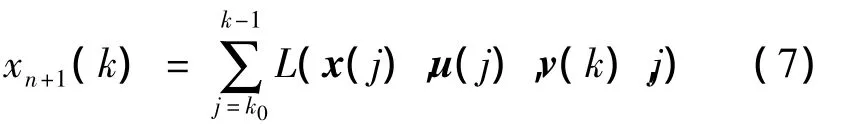
规定xn+1(k0)=0，则有:

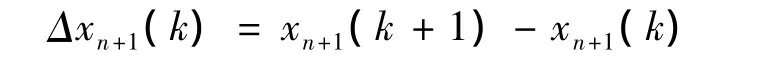
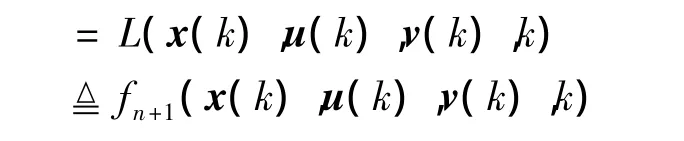
令

则状态方程可写成:

称为增广系统的状态方程。得到的非线性规划问题为:

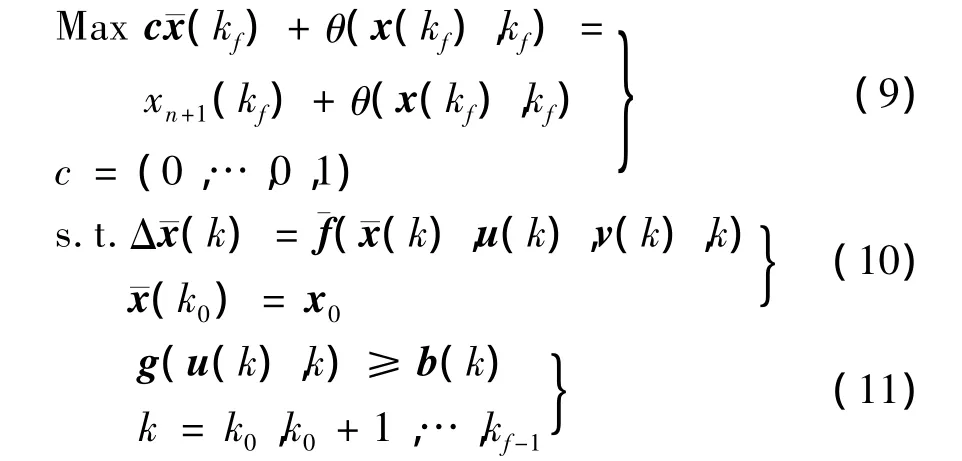
考虑拉格朗日函数:

拉格朗日函数化为:

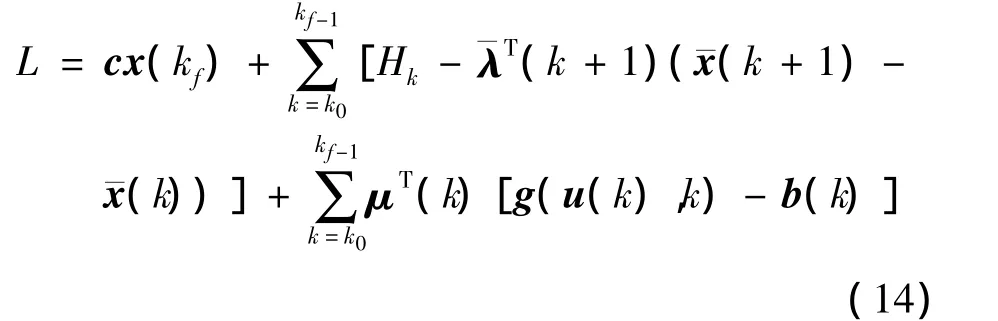
非线性规划问题式(9)～式 (11)的解满足的必要条件如下:

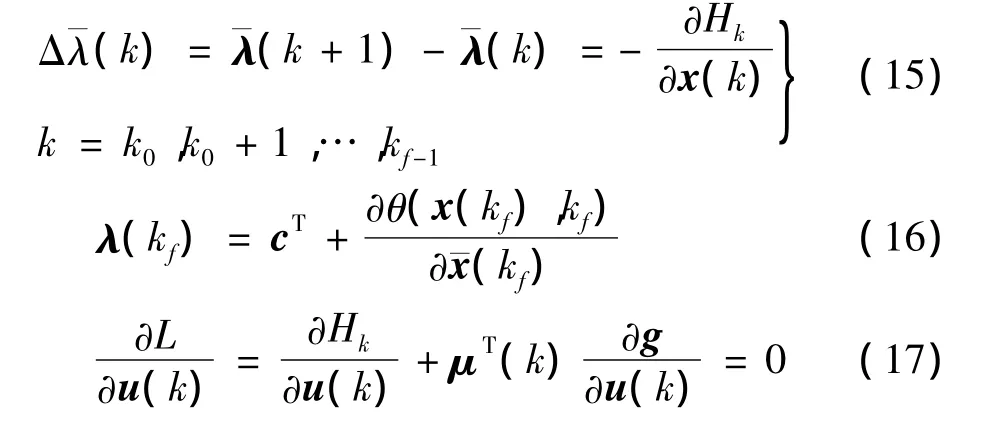
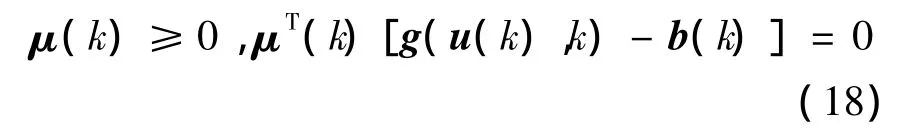
应用非线性规划问题解的充分性条件的定理，如果Hk是凹的，g(u(k)，k)是凸的，那么条件式(17)、式(18)保证 u(k)使式(13)作为 u(k)的函数，在约束条件g(u(k)，k)≥b(k)下达到最大值，即条件式(17)、式(18)可用条件

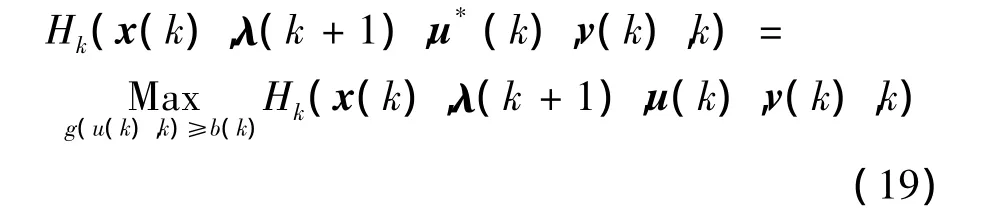
代替。由必要条件式(16)及 c=［0，…，0，1］得:

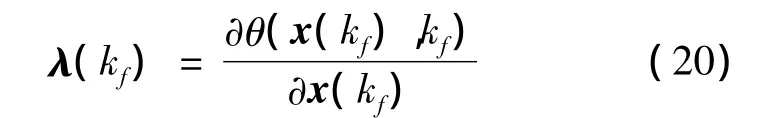
又由于Hk不显含xn+1，因此，式(15)的最后一个方程为 Δλn+1(k)=0，于是 λn+1(k)=1，哈密顿函数可改写为:

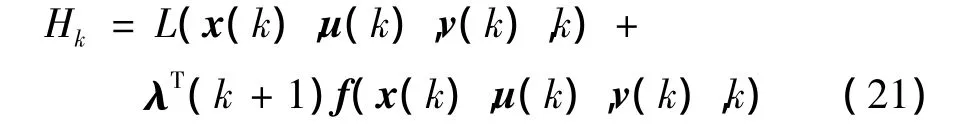
这样，上述必要条件归结为:x*，u*，λ*满足

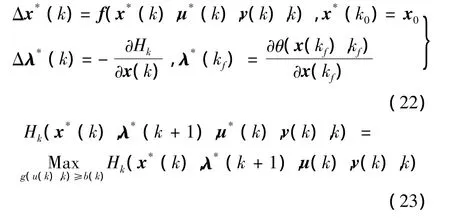
4 仿真及分析

下面以一条典型的战略导弹弹道为例，进行导弹中段智能突防的仿真研究。

通过计算，得出弹头不作机动时的弹头轨迹和EKV的拦截轨迹，如图4所示。仿真结果表明，拦截结束时脱靶量小于3 m，EKV拦截成功，验证了本文所建拦截器模型的正确性。

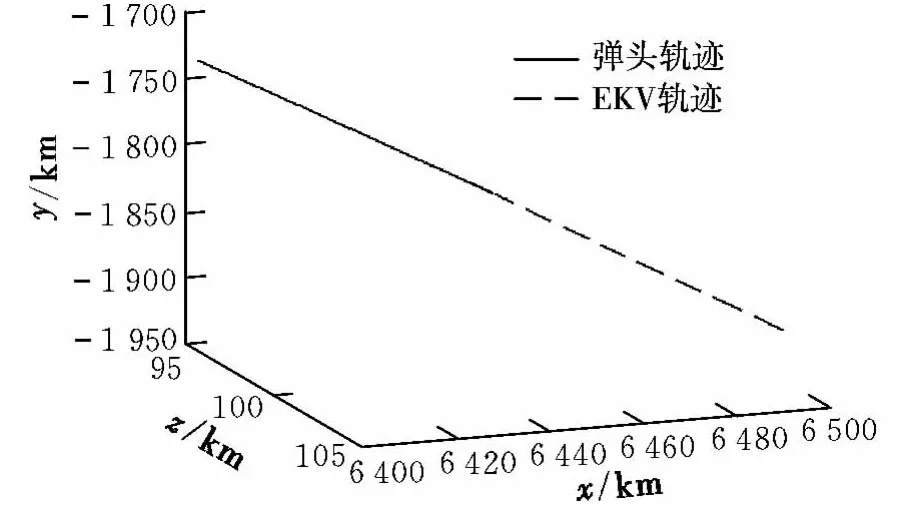
图4 弹头与EKV的飞行轨迹Fig.4 Flight trajectory of the warhead and the EKV

本文设定EKV的导引系数K=3，弹头机动时间t1=1 536.96 s，持续时间Δt=8 s。当弹头用本文的微分对策模型得出的控制量进行机动时，得到的脱靶量为8.5 m，EKV拦截失败，验证了本文方法的有效性。

将目标弹头作垂直于发射系Oxy平面的负向机动和不作机动时的EKV横向视线角(λx)变化和视线角速率()进行对比，如图5和图6所示。

图5 EKV横向视线角变化曲线Fig.5 Horizontal line of sight angle curve of the EKV

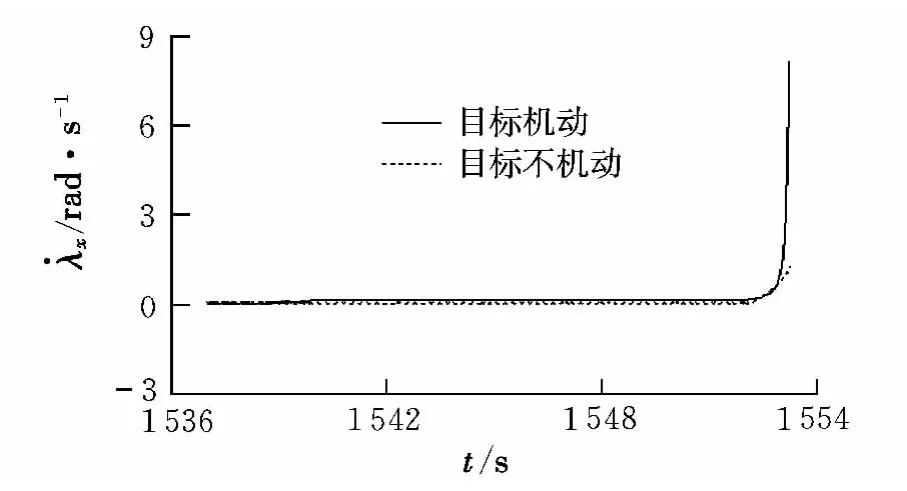
图6 EKV横向视线角速率变化曲线Fig.6 Horizontal line of sight angular rate curve of the EKV

由EKV的拦截结果可知，当弹头不作机动时，扩展比例导引律能有效抑制视线角速率的发散，使脱靶量很小;当弹头利用微分对策的方法进行智能机动时，EKV测得的视线角和角速率出现了较快的发散。

5 结束语

本文基于微分对策理论，研究了弹头在中段飞行中的机动突防问题，将弹头和EKV看作“二人零和”博弈的主体，建立了微分对策模型，得出弹头的最优规避策略。仿真结果验证了方法的有效性，得到的最优策略集可制成指令库装订到弹头上。该方法为微分对策理论在弹上的实现提供了重要的理论参考。

［1］ 袁俊.导弹防御系统的弹道导弹突防［J］.上海航天，2005，(1):48-51.

［2］ 朱˙费登伯格，让˙梯诺尔.博弈论［M］.黄涛，等 译.北京:中国人民出版社，2010:53-65.

［3］ 孙守明，汤国建，周伯昭.基于微分对策的弹道导弹机动突防研究［J］.弹箭与制导学报，2010，30(4):65-68.

［4］ 冯杰.弹道导弹“主动规避”式机动突防技术研究［D］.西安:第二炮兵工程学院，2007.

［5］ 汤一华，陈士橹，万自明.基于零控脱靶量的大气层外拦截中制导研究［J］.飞行力学，2007，25(3):34-37.

［6］ Wang L，Jing Z，Yang Y，et al.Analysis and simulation on the intercepting performance of EKV［C］//System Simulation and Scientific Computing，ICSC 2008.Asia Simulation Conference-7th International Conference on IEEE，2008:643-646.

［7］ 徐增.基于天基预警系统的导弹被动段弹道估计算法研究［D］.哈尔滨:哈尔滨工业大学，2006.

［8］ 雍恩米，唐国金，罗亚中.弹道导弹中段机动突防制导问题的仿真研究［J］.导弹与航天运载技术，2005，(4):13-18.