科恩否定原理的局限及其尝试性修正

李 铁，张大松

(1.武汉商贸职业学院通识教育学院，武汉 430205;2.华中师范大学 马克思主义学院，武汉 430079)

科恩否定原理可表述为:对于任何E和H，如果E报道物理上可能的一个事件或一些事件或一个合取式，那么，如果 S［H，E］＞0，则 S［﹁H，E］=0［1］177。在批判数学概率逻辑的局限性基础上，科恩否定原理体现出自身的理论价值和应用价值，但它本身仍然存在一定的局限性，这种局限性表现为理论自身的不一致性和应用上的不恰当性。其根本原因在于否定原理采取了过强的否定策略。

一、科恩否定原理的实质

科恩的否定原理可表述为，任一命题H被赋值大于零级的支持等级时，否定H只能获得零级的支持等级。科恩给出了如下的证明:对于任一全称量化条件命题

(1)∀x(Rx→Sx)，它的否命题为

(2)∃x(Rx∧﹁Sx);

由于(1)或蕴含(1)的命题得到了成功检验，故可对它指派大于零的支持等级。但是由于(2)不是全称量化条件命题，因而它不可检验并指派支持等级，它的支持等级只能从蕴含它的命题的检验结果而获得。但这一结果必定是零。例如，如果

(3)∀x(Fx→Kx)

(4)∀x((Fx→Kx)→(Rx∧﹁Sx))

都能得到有力检验结果，那么就能分别通过合取原理和后承原理得到，(3)和(4)的合取所具有的归纳支持至少与(2)的支持等级一样。因为(2)是这一合取式的后承。但是，我们又可知，(4)所通过的检验一定是(1)未能通过的;如果(1)具有正支持等级，那么就不可能通过检验以间接的方式确立(2)的正支持等级。所以(2)的支持等级不可能大于零。证毕［1］177－178。

否定原理实际上要表明的是，如果假说H基于证据E得到了大于零级的支持，那么基于同样的证据就不能对它进行否定，同时基于同样证据的其他假说相对于H不具有竞争地位。它有着深刻的内涵。首先，在性质上，它表明归纳概率逻辑的句法结构与数学概率逻辑的句法结构不可通约。在数学概率中，否定原理是互补的，即Pr(﹁p)=1－Pr(p)，而在归纳支持中，否定原理不具有这种减法性质，是非互补的。因此归纳支持是一种不同于数学概率的独立的逻辑句法。其次，在方法论上，它强调不同权重的证据对假说的归纳支持等级的影响。这种测度是通过相关变项法得以实现的。第三，它体现了局部支持的思想，当假说基于背景知识得到大于零级的支持时，那么它不能被否定。否定原理是科恩理论最具特色的规则，同时也是科恩整个理论体系的基石，但它在理论和应用方面却存在一定的局限。

二、科恩否定原理的局限性

科恩否定原理的局限性主要体现在理论内部及其推广应用上。理论上的局限，主要是否定原理会导致系统内的逻辑矛盾。应用上的局限主要是否定原理对假说保护过强，拒斥竞争假说的合理性，不符合科学实际。导致这种局限性的主要原因是否定原理过强的否定性。

理论内部的非一致性体现在如下两种情况中。

情况1 科恩在给出否定原理的证明后即设想:假设假说H1基于证据E得到大于零级且不完全的归纳支持，同时H2由于解释了H1中反常的E，故 H2→﹁H1，且 H2的支持等级大于 H1，令:

(1)S［H1，E］＞ i/n+1，S［H2，E］＞ j/n+1，(n＞j＞i＞0)

(2)由否定原理，可得:S［﹁H1，E］=0;

(3)由 H2→﹁H1和后承原理，可得:S［﹁H1，E］≥ S［H2，E］＞0;

(4)因此(2)和(3)矛盾。

对于这一矛盾，科恩认为因为逻辑推论是正确的，又没有理由对相关变项提出质疑，那么一定是相关变项集的排序出了问题，因此重新对相关变项集的序列进行考察可以解决矛盾。但科恩的这个理由与其归纳支持逻辑的整体思想相冲突。在科学实际中，科学家对相关变项集的排序是审慎的，变项的证伪能力同样是依据经验和已被科学共同体接受的背景知识确定的，如果一出现矛盾就修正相关变项集，无疑会使科学实践迁就于逻辑定理。科恩在此陷入了自相矛盾，一方面坚持经验主义原则，一方面又使经验让步于逻辑规律;更重要的是，它与归纳概率逻辑的局部支持宗旨相悖。

情况2 设H1和H2属于同一竞争假说集，令S［H1，E］＞ i/n+1，S［H2，E］＞ j/n+1。

(1)由否定原理得:S［﹁H1，E］=0，S［﹁H2，E］=0;

(2)由析取原理得:S［H1∨﹁H1，E］=i/n+1，S［H2∨﹁H2，E］=j/n+1;

(3)由二值逻辑排中律得:H1∨﹁H1=1，H2∨﹁H2=1;因此(H1∨﹁H1)↔(H2∨﹁H2);

(4)由齐一性原理和(3)得:S(H1∨﹁H1，E)=S(H2∨﹁H2，E);

因此(2)和(4)矛盾。

科恩虽然利用后承原理对这一矛盾提出自己的辩护，但已被证明他的反驳仍然是无效的。同时有学者认为，导致矛盾的根本原因在于相关变项法的语义解释与经典二值逻辑的语义解释之间存在矛盾。经典二值逻辑要求在同一思维过程中必须遵循排中律，但是相关变项法允许H和﹁H同时为零。这样的批评是合理的，但这样一来就要对二值逻辑的语义解释和相关变项法的语义解释同时做出修正，这样不仅使逻辑系统的修改代价过大，而且亦不能解决情况1中出现的矛盾。

科恩否定原理在应用上的不恰当性主要指基于同样的证据否定原理不承认竞争假说的地位，即假说H一旦得到某种程度的归纳支持，那么同样的证据E不支持﹁H获得大于零级的支持。结合物理学史上著名的光本性实验，可以更直观地发现否定原理在应用上的不恰当性。

光的本性论在历史上曾有两种观点，惠更斯首先提出波动说，随后牛顿提出粒子说。由于牛顿在当时的影响巨大，因此多数人支持光的粒子说。到底光的本质是粒子的还是波动的?科学家们设计了这样的实验，使光在两种不同的介质中传播，观察光从一种介质到另一种介质时发生的情况。实验以空气和玻璃作为两种不同的介质，结果显示，光从空气到玻璃面时既发生了反射又发生了折射。牛顿对此的解释是，光的这种既反射又折射“痉挛”是由以太传递给粒子的。惠更斯则用几何学理论解释了光的反射和折射。这一实验表明，基于相同的证据，相互竞争的假说都可得到一定程度的支持，甚至是相同等级的支持。但显然科恩的否定原理与该实验不符:首先通过相关变项法，可得粒子说和波动说的归纳支持等级，其中相关变项只有一个——光传播的介质，变素只有玻璃 v1，R表示“是光”，S表示“是粒子”，F表示“是波”。

对于粒子说H1有:

(1)S［∀x(Rx→Sx)，∃x(Rx∧Sx∧T1x)］=1/2

(2)S［∀x(Rx→Sx)，∃x(Rx∧Sx∧T2x∧v1)］=2/2

因此，S［H1，E］≥2/2。

对于波动说H2有:

(1)S［∀x(Rx→Fx)，∃x(Rx∧Fx∧T1x)］=1/2

(2)S［∀x(Rx→Fx)，∃x(Rx∧Fx∧T2x∧v1)］=2/2

因此，S［H2，E］≥2/2。

根据否定原理，S［H1，E］＞ 0，那么 S［﹁H1，E］=0;又 H2→﹁H1，可根据后承原理得 S［H2，E］＜0。同理可证S［H1，E］＜0。可见否定原理在此自相矛盾，它与科学实际不符。

综上所述，科恩系统的不一致性和应用的不恰当性都与否定原理有关，因此有必要考察否定原理本身的合理性。

否定原理存在局限性的主要原因是采取了过强的否定策略。所谓过强的否定策略是指由于坚持了二值逻辑的矛盾律，导致归纳支持的弱肯定性与矛盾律的强否定性不协调。通过分析科恩对否定原理的证明，可以发现这种不协调性。

科恩否定原理可以用一个蕴含式表示:(S［H，E］＞0)→(S［﹁H，E］=0)，该蕴含式前件体现了科恩的归纳支持思想，蕴含关系即为科恩的否定规则，后件为否定规则的结论。在科恩那里，全称条件句假说H的支持等级是通过对特称命题的逐级检验确定的，其推理模式为(T表示假说通过的实验检验):

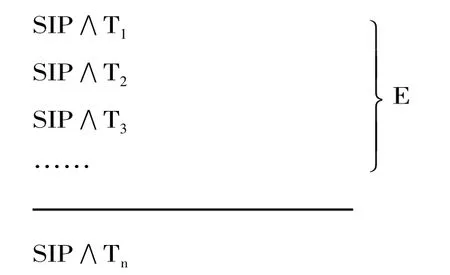
SIP与 SAP为差等关系，从 SIP不能必然推出SAP，因此SAP获得的支持等级是归纳的。又SOP(﹁SAP)为特称命题，其支持等级不可通过直接检验确定，而只能通过检验SEP间接地确定。因为SIP与SEP为矛盾关系，SIP通过的检验必然是SEP无法通过的，所以SEP的支持等级必然为零级。可见，否定原理是以归纳推理和矛盾律为逻辑内核的，依据前者全称命题H获得大于零级的支持等级，依据后者﹁H只能得到零级的支持。正因如此，科恩的否定原理在整体的逻辑性上出现了弱肯定与强否定的不协调，这种不协调性也必然会导致科恩整个逻辑系统的不一致性。事实上，从二值逻辑的观点看，当S［H(SAP)，E］＞0时，即 S［H，E］的实质为 SIP，那么，S［﹁H，E］则为SOP，显然，S［﹁H，E］不必然为零。正是因为科恩采取了不协调的逻辑规则，使得否定原理在应用中出现“怪论”，即SIP成立时，SOP不成立。

科恩否定原理在逻辑上的不协调也必然导致语义解释上与实际不符。科恩否定原理在语义解释上，不允许相同的证据对竞争假说都给予大于零级的支持，而在证据理论中，同一证据可以支持不同的假说。证据的基本特征为语句性、经验性和相关性。证据语句在不同的语境下，可以有不同的指称，其相关性也随之变化。对于同一领域的竞争假说，证据都可起到相应的支持作用，这种支持作用既可能体现为对竞争假说提供不同程度的支持(甚或相同程度的支持)，也可能体现为对竞争假说不同部分的支持。因此在科学实际中，允许相互矛盾的假说并存。而科恩通过严格的矛盾律，拒斥了竞争。虽然这对假说给予了最大程度的保护，但不符合科学实际。

综上，科恩否定原理内部存在弱肯定与强否定之间的矛盾，它必然导致系统的非一致性和不恰当性。要消除这种矛盾，必须对否定原理进行相应的修正。

三、科恩否定原理的尝试性修正

科恩否定原理弱支持与强否定间的矛盾可以通过两种途径来调和，一是保留强否定，对弱支持进行加强修正;另一方法是，保留弱肯定，对强否定采取相应的弱化。考虑到科恩体系的整体特点以及它的理论和实践价值，第一种途径将使得科恩的系统更为复杂，其结果将不利于局部辩护，因此本文采取了第二种策略来修正科恩的否定原理。

科恩的归纳支持体现了局部辩护的思想，但是科恩并没有对局部支持进行定量研究，只是考察某一S是P成立的条件，从而推出在同样条件下所有S是P，这样的支持太弱了，因为它不能保证在同样条件下所有S是P。进一步的，他否定了在同样条件下有S不是P的可能性。因此，在维护局部支持的前提下，应该对整体否定进行弱化。另一方面，在科学实际中，允许矛盾的存在，因此为了使归纳概率逻辑具有更好的应用推广性，应当在放弃排中律的同时，也放弃矛盾律。基于这样的考量，可以在三值逻辑的框架下对否定规则进行修正。

科恩的逻辑系统是一个等级系统，这与次协调逻辑的等级序列有共性。就是说，任一命题的归纳支持都是依靠相关变项的证伪等级来确定的，那么相应地，对它的否定也应该具有这样的等级性。同时，由于次协调逻辑不严格遵守二值逻辑的矛盾律，因此它的真值允许有第三值(如表1所示)。

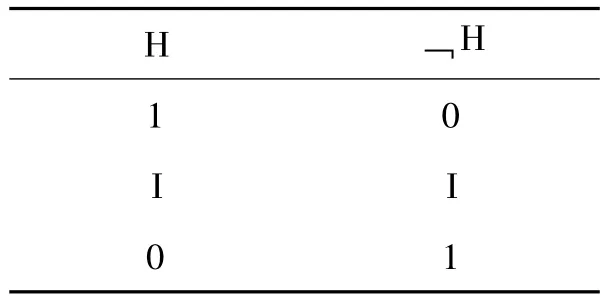
表1 真值表

但是在科恩逻辑系统中，任一命题都可通过实验检验确定它的支持等级，因此H不取I，它可取［0，1］之间的值。这样我们可以重新构造归纳概率逻辑的真值表，如表2(α表示H的取值)。

表2 真值表

由此，在归纳概率逻辑中任一命题H的值可以有3种情况，其中复合命题的赋值规则遵守三值逻辑的运算规则。在这一框架下，可对否定原理作出修正:

(1)S［H，E］=1 时，S［﹁H，E］=0

(2)0＜S［H，E］＜1 时，S［﹁H，E］=I

(3)S［H，E］=0时，S［﹁H，E］=1

由于归纳支持的相关变项法对相关变项集合不假定完全的样本空间，它是一个开放的集合，允许任何时候当新的相关变项被发现时进入到该集合中，因此H的归纳支持等级在事实上永远无法取到1，这样修正方案(1)可去除。当S［H，E］=0时，说明假说H在经验中无法被观察到，也无需设计实验来检验，修正方案(3)可去除。因此修正后的否定原理可表述为:对于任何E和H，如果E报道物理上可能的一个事件或一些事件或一个合取式，那么，如果 S［H，E］＞0，则 S［﹁H，E］=I。

科恩否定原理经三值逻辑框架的修正，会具有多方面的意义。

第一，它放弃了矛盾律和排中律，这样相关变项法的语义解释和三值逻辑的语义解释相调和。鞠实儿教授在对科恩系统进行批判时，指出科恩系统的不一致性和不恰当性的根本原因在于相关变项法的语义解释和二值逻辑语义解释相矛盾。修正后的否定原理以三值逻辑为框架，其语义解释也具有三值性，即:(1)一个可检验命题H具有j(j＞0)级的归纳支持等级，当且仅当它在至少有一可能世界Wj中为真;(2)当H具有j(j＞0)级的归纳支持等级时，其否命题﹁H具有不确定的归纳支持等级，亦即不能确定﹁H在任何可能世界Wj中必假。

第二，否定原理弱肯定与强否定之间的矛盾得以调和，使得归纳概率逻辑系统本身更加一致，在应用上也更加恰当。可考察上文情况2在否定原理修正后的情形。设H1和H2属于同一竞争假说集，令 S［H1，E］＞ i/n+1，S［H2，E］＞j/n+1。

(1)由否定原理得:S［﹁H1，E］=0，S［﹁H2，E］=0;

(2)由析取原理得:S［H1∨﹁H1，E］=I，S［H2∨﹁H2，E］=I;

(3)由赋值规则得:H1∨﹁H1=I，H2∨﹁H2=I;因此(H1∨﹁H1)↔(H2∨﹁H2);

(4)由齐一律得:S(H1∨﹁H1，E)=S(H2∨﹁H2，E)=I;

因此(3)和(4)不矛盾。

可见，修正后的否定原理不会导致系统矛盾。同时修正后的否定原理给予了竞争假说一定的地位，但它又不会对被验假说构成威胁，因为I的支持力低于任一大于零级的支持等级的支持力。从而其推广应用也更加宽泛，更能贴近科学的实际。比如，基于反射和折射实验，光的粒子性得到大于零级的支持时，光的波动性不被否定，反之亦然。

第三，修正后的否定原理采取弱否定策略，大大提高了它的辩护功能。科恩系统在对休谟问题的解决上曾遭到这样的批评:由于归纳概率逻辑系统的局部化程度过高，因此它们的辩护性过低。综观科恩系统的全貌，可以看到科恩一方面努力保持着他的系统在正向(归纳支持)上的开放性，一方面又在负向(否定规则)上是完全封闭的。其原因是，科恩在假说提供归纳支持的同时在竭尽全力地对它给予最大程度的保护。因此，他不得不构造复杂的逻辑句法，不断提高其系统的局部化程度。修正方案对否命题赋值为I，这一策略既打破了科恩系统在负向上的封闭性，同时对假说又不构成威胁。因此，修正方案虽然未触及科恩的局部支持系统，但它对否定律的弱化使得整个系统更加柔性，从而能大大提高它的辩护功能。

当然，还应看到，尽管对否定原理的技术性修正使得科恩体系在理论上更一致、应用上更恰当，但在整体上它仍然面临着语境等方面的困境。正如凯伯格所说:“局部归纳法无论在技术上作出怎样的改进，它都面临一个一般性的挑战，即如何判别由最初的不同资料或背景知识所导致的意见分歧;局部归纳法不可能解决这一问题，除非它适当扩展其归纳辩护所依据的语境，但这样一来它又不可避免地趋向整体辩护和整体归纳。”［2］因此，在局部辩护纲领的指引下，非帕斯卡概率逻辑的研究任重道远。

［1］Cohen L J.The Probable and the Provable［M］.Loden:Oxford University Press，1977.

［2］何向东.“归纳问题”的逻辑哲学研究述评［J］.哲学研究，2005(12):79 －83.

［3］鞠实儿.非巴斯卡归纳概率逻辑研究［M］.杭州:浙江人民出版社，1993.

［4］张巨青.科学逻辑［M］.2版.长春:吉林人民出版社，1987.

［5］张大松.科学确证的研究进路探微［J］.江海学刊，2009(6):24－29.