一类比率依赖模型的全局稳定性

胡宝安，李 兵，邹晓健

(1.军事交通学院 基础部，天津300161;2.军事交通学院 政治部，天津300161)

捕食者与食饵间的捕食现象在自然界中普遍存在，研究捕食者与食饵随时间的演变规律，实施人工干预实现对种群有效的保护、合理的开发和利用，是生物界与生物数学方面的重要研究课题之一。借助于微分方程的理论和方法建立合理的数学模型，是研究这一课题的重要方法之一。从数学的观点来看，要揭示两种群的变换规律，预测它们的未来趋势，就需要研究微分方程解的特性，特别是解的全局渐近稳定性。

1 捕食模型

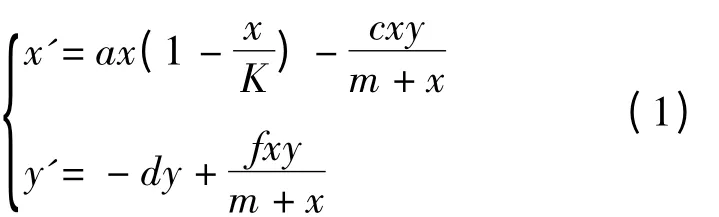
用来描述捕食与食饵关系的经典数学模型是具有第二功能性函数的Lotka-Volterra 模型［1］，即式中:x为食饵数量;y为捕食者数量;a、K、c、m、f、d均为正数且分别表示食饵的自然增长率、环境容纳量、捕食者的捕获能力、饱和系数、转化系数以及捕食者的死亡率。

模型(1)的数学分析表明，此模型存在2 个不足［2-3］:一是当环境容纳量K增大时，捕食者数量增加而食饵数量却减少，且随着K的增大模型(1)的正平衡点由稳定变为不稳定;二是模型(1)的边界平衡点是不稳定的，这说明捕食者和食饵种群不会同时绝灭，这些和实际不相符合。

为了改变这些不足，人们在模型(1)的基础上，将“比率依赖”理论［1-6］引入建模过程，提出了更加符合实际的比率依赖的捕食模型［2-6］。其中最具代表性的是文献［2］中的模型，即

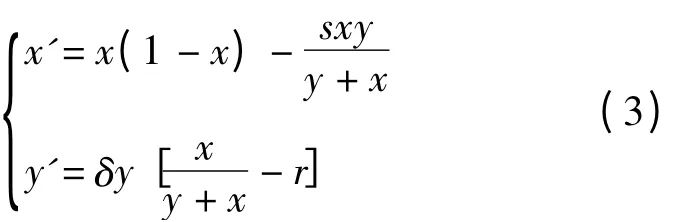
模型(3)有2 个边界平衡点(0，0)和(1，0)，当r∈(0，1)，s∈(0，1/(1-r))时存在唯一的正平衡点(x*，y*)，其中，x*=1-s(1-r)，y*=

模型(3)不仅消除了模型(1)的不足，并且得到了比模型(1)更丰富的结果。但是文献［2］对模型(3)平衡点全局稳定性的讨论不够全面，并提出了如下3 个猜想。

猜想1 当r≥1，1 ＜s≤1 +δr时，模型(3)的边界平衡点(1，0)是全局渐近稳定的。

猜想2 当0 ＜r＜1，1 ＜s＜1/(1-r)且δ(1-r)≥1 时，模型(3)的正平衡点(x*，y*)是全局渐近稳定的。

猜想3 当0 ＜r＜1，1 ＜s≤1 +δr且δ(1-r)＜1 时，模型(3)的正平衡点(x*，y*)是全局渐近稳定的。

这3 个猜想对于更加全面准确地揭示两种群在不同环境条件下的变化规律、发展趋势有重要的地位，已有结果都是在猜想条件的基础上增加条件进行证明。本文通过作适当变换和巧妙构造Lyapunov 函数的方法，在不附加条件的基础上证明了这些猜想的正确性。

作变换u=x/y，则模型(3)变换为

显然模型(4)满足初值x(0)＞0 和y(0)＞0的解是非负的，且有

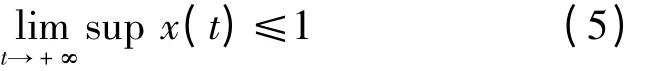
2 猜想1 的证明

结论1 当r∈［1，+∞)，s∈(1，1 +δr］时，模型(3)的边界平衡点(1，0)是全局渐近稳定的。

证明 因为r≥1，所以由模型(3)解的非负性和第2 个方程可得

从而有

(1)当r∈［1，+ ∞］，s∈(1，δr)时，由模型(4)解的非负性和第2 个方程及式(5)可得

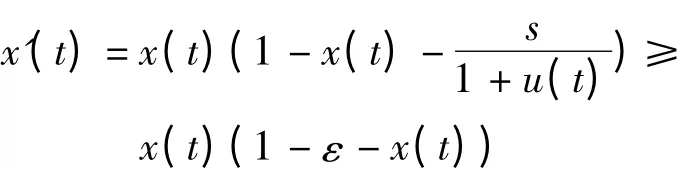
(2)当r∈［1，+ ∞)，s∈［δr，1 + δr］，δr＞1时，模型(4)只有平衡点E(0，0)且为鞍点。等倾线x=f(u)与x=g(u)满足g(u)＞f(u)(u＞0)(如图1 所示)且有

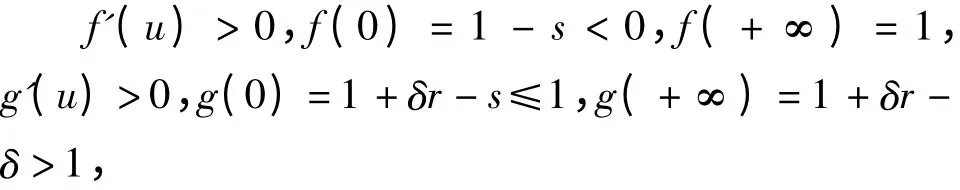
记

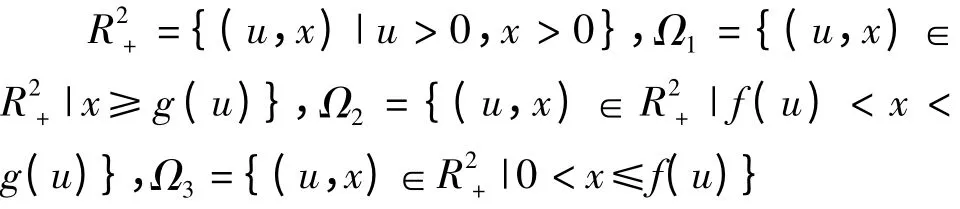
图1 流形分析

模型(4)在Ω1内没有平衡点，所以从Ω1出发的解将垂直穿过x=g(u)进入Ω2;又因为E(0，0)为鞍点，所以从Ω2出发的解将水平穿过x=f(u)进入Ω3，并将最终停留在Ω3内(如图1 所示)。在Ω3内x＇(t)＞0，u＇(t)＞0 且，从而模型(4)的任意正解都有

(3)当r∈［1，+ ∞)，s∈(1，1 + δr］，δr≤1时，证明同上。

3 猜想2 的证明

结论2 当r∈(0，1)且δ(1-r)≥1 时，模型(3)的正平衡点(x*，y*)全局渐近稳定。

证明 在结论2 的条件下，模型(4)存在3 个平衡点E0(0，0)，E1(0，¯u)，E(x*，u*)，其中¯u=

要证明模型(3)的正平衡点(x*，y*)全局渐近稳定，只需证明模型(4)的正平衡点(x*，u*)是全局渐近稳定的。

模型(4)在E0(0，0)处的Jacobian 矩阵为

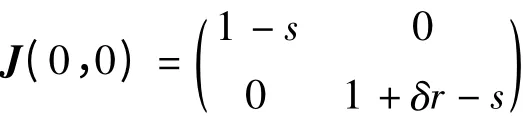
模型(4)在E1(0，¯u)处的Jacobian 矩阵为

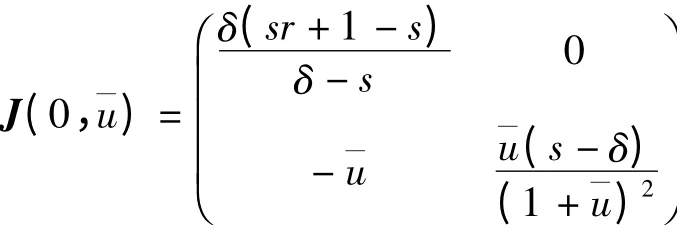
模型(4)在E(x*，u*)处的Jacobian 矩阵为

其行列式恒大于0，其迹为

由结论2 的条件可知，1 ＜s＜1/(1-r)＜1 +δr且δ ＞s，所以E0(0，0)和E1(0，¯u)均是鞍点不稳定;同时有

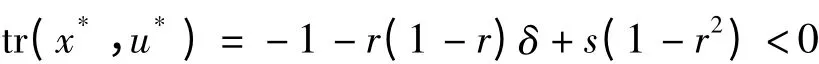
即正平衡点E(x*，u*)局部渐近稳定的。为了证明正平衡点的全局渐近稳定性，构造Liapunov 函数:

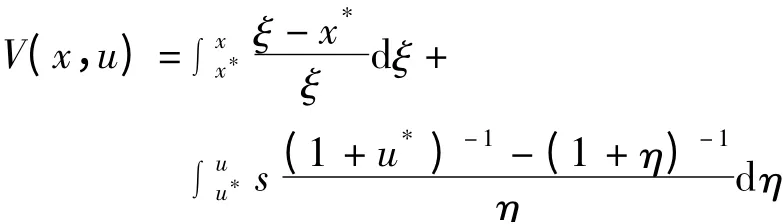
沿模型(4)的解求导，可得

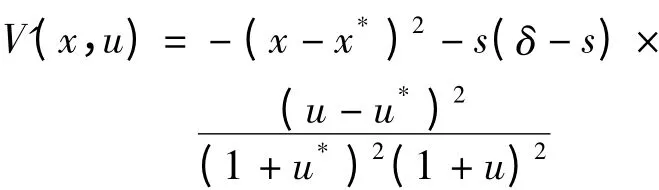
因为δ ＞s，所以对任意的(x，u)≠(x*，u*)都有V＇＜0，从而模型(4)的正平衡点E(x*，u*)全局渐近稳定，系统(3)的正平衡点(x*，y*)是全局渐近稳定的。

4 猜想3 的证明

结论3 当r∈(0，1)，s∈(1，1 + δr］，δ(1-r)＜1时，模型(3)的正平衡点(x*，y*)全局渐近稳定。

证明 在变换u=x/y下，将模型(3)改写为

结论3 的条件暗含s≤1 +δr＜1/(1-r)，此时模型(6)存在2 个平衡点其中

构造Liapunov 函数:

沿模型(6)的解求导，可得

因为1 +δr-s≥0，1 +δr-δ ＞0 且u＞0，u*＞0，所以对任意的(u，y)≠(u*，y*)都有V＇＜0，从而模型(6)的正平衡点E(u*，y*)全局渐近稳定，也即系统(3)的正平衡点(x*，y*)是全局渐近稳定的。

5 结 语

对一类具有比率依赖的捕食模型进行定性分析，通过变换和构造Liapunov 函数的方法，证明了文献［2］所提出的关于平衡点全局稳定性的3 个猜想是正确的。为更全面准确地揭示捕食者与食饵间发展规律、预测其变化趋势、实现种群规模的有效控制提供理论依据。

［1］ Freedman H I. Deterministic Mathematical Models in Population Ecology［M］. Marcel Dekker，New York，1980:39 –45.

［2］ Kuang Y，Beretta E. Global qualitative analysis of a ratio-dependent predator-prey system［J］. J. Math. Biol.，1998，36(2):389 –406 .

［3］ Kuang Y. Rich dynamics of Gause-type ratio-dependent predator-prey system［J］. The Fields Institute Communications，1999，21(4):325 –337.

［4］ Beretta E，Kuang Y. Global analyses in some delayed ratio-dependent predator-prey systems［J］. Nonlinear Analysis，1998，32(3):381-408.

［5］ 高建国. 基于比率的Holling-Tanner 系统全局渐近稳定性［J］.生物数学学报，2005，20(2):165-168.

［6］ 苑学梅，胡宝安，陈博文，等. 一类具有广义Logistic 增长的比率型捕食模型的定性分析［J］. 生物数学学报，2011，26(2):298-302.