微积分在大学物理教学中的重要应用

朱叶青

（南京师范大学泰州学院 信息工程学院应用物理系，江苏 泰州225300）

0 引言

大学物理是理工科大学面向一、二年级开出的，融合了力、热、光、电和原子物理等基本领域的一门重要的必修基础课，比起中学物理来说，大学物理更加接近于“现实状态”，所研究的运动为加速度时刻发生变化的变速运动，功为变力所做的功，各种类型带电体在空间各个不同点形成的电场在变，磁场也一直在变化等等，此时中学物理所形成的处理“恒定”问题的技能已不再适用，必须建立一套适用于处理“动态”物理问题的新的方法，即微积分的方法.

微积分是指把复杂的问题进行时空上的有限次分割，在有限小的范围内进行近似处理，然后让分割无限地进行下去，局部范围无限变小，则近似处理也就会越来越精确，这样在理论上得到的结果。微分是指在理论分析时，把分割过程无限进行下去，局部范围便会无限小，积分是指把无限小个微分元求和[1]，微积分是高等数学中比较重要的一个分支. 从大学物理和高等数学的发展史中可以看出两者相互联系，相互促进，物理学提供相应的“现实模型”，高等数学提供“抽象的解决方法”，所以高等数学是大学物理课程的必备基础与工具.

1 微积分在大学物理中的重要应用

下面主要从大学物理中力学和电磁学两部分的几道例题分析一下微积分的重要应用：

例题1 跳水运动员沿铅直方向入水， 接触水面时速率为v0，入水后地球对他的吸引和水的浮托作用相抵消， 仅受水的阻碍而减速，自水面向下取Oy 轴，其加速度为ay=-，vy为速度，k 为常量，求入水后运动员速度随时间的变化[2].

解：将运动员视为质点，当运动员沿着铅直方向运动时，运动速度vy随着时间t 变化，即vy=vy（t），在时间间隔Δt 内，质点速度增量为Δvy=vy2-vy1，当Δt→0 时，此时加速度就趋于一个极限值，即瞬时加速度（也称加速度）ay，

设入水时为计时起点，当t=0 时vy=v0，运动过程中t 时刻的速度为v，将上式两侧分别以vy和t 为积分变量，以和k 为被积函数，则有

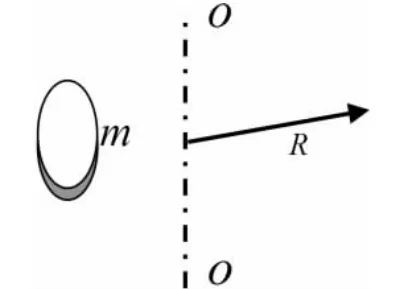
图1

上面例题是质点运动学的一个典型例题，解题思路是先运用数学导数的概念，即通过求平均变化率的极限来得到瞬时加速度，列出重要的数学表达式， 把数学导数的知识巧妙地应用到物理学当中去，接下来通过给定的初始条件进行定积分，即对微元进行求和，最终算出结果，把看似复杂的变速问题变得更加简单化.

例题2 如图1 所示，圆盘的质量为m、半径为R，求以O 为中心，将半径为R/2 的部分挖去，剩余部分对OO 轴的转动惯量[3].

解：因为圆盘上的质点是连续分布的，所以求解此题可以用两种方法：一是由转动惯量的定义式来计算，即把圆盘分成许多细圆环带，其中半径为r，宽度为dr 的环带质量为二是补偿法，可将剩余部分的转动惯量看成是原大圆盘和挖去的小圆盘对同一轴的转动惯量的差值.

比较方法一和方法二，明显可见方法一的便利之处，求解过程相对简捷，从方法一可看出微积分知识和简单物理模型的密切结合， 不仅能使学生更加深入地理解基本物理理论知识，而且能够使学生开阔思路，触类旁通，这也是物理教学比较重要的一方面.

例题3 设半径为R 的带正电薄圆盘的电荷面密度为σ，并以角速度ω 绕通过盘心垂直盘面的轴逆时针转动， 求圆盘中心处的磁感强度[3].

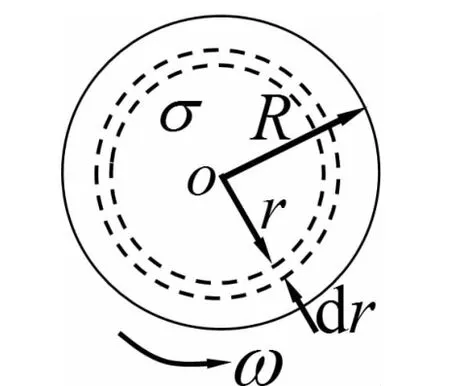
图2

解：方法一：利用毕奥萨-伐尔定律得到的圆电流在圆心处的磁感强度值为B=μ0I/2R 求解，其中I 为圆电流，R 为圆电流半径.首先采用微分知识将圆盘分成许多细圆环带，其中半径为r，宽度为dr 的环带的电荷为dq=σ2πrdr，因圆盘以角速度ω 绕轴O 旋转，则此转动圆环带相当的圆电流为：

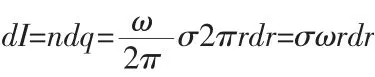
根据以上关系得圆盘上细圆环带在盘心处磁感强度值为：

代入初始条件进行定积分，可得整个圆盘转动时盘心处磁感强度值为：

已知圆盘带正电，故磁感强度的方向垂直纸面指向外侧.

方法二： 根据毕奥-萨法尔定律求得的运动电荷产生的磁感强度求解.首先采用的微分方法同方法一，得dq=σ2πrdr，因为角量和线量存在关系v=rω，所以有：

此式方法一已得到，故利用积分知识同样得到方法一的结果.

以上例题主要体现了微积分在电磁学方面的重要应用，虽然从不同微量之间的关系去探讨问题，最终都得到了精确的解，由此可见微积分的奇妙之处，只要选择合适的微元，找好相应的方法，就可以完美地实现物理模型的由复杂到简单、由变量到恒量、由未知到已知的转变.

2 结语

微积分作为高等数学中一个比较重要的分支，在大学物理教学中起着举足轻重的作用，它不仅是教学工具的应用，也是一种思维方法的应用，教师在教学过程中要巧妙地将微积分融入到大学物理教学中去，恰当地取好微元，分析好元过程和元贡献，确定好积分上下限，最终可以解决许多复杂的物理问题， 使得学生增强学习物理的信心，达到事半功倍的教学效果.

［1］黎定国.大学物理中微积分的思想方法浅谈[J].大学物理，2005,24（12）:52－54.

［2］漆安慎，杜婵英.力学[M].北京：高等教育出版社，1997.

［3］马文蔚.物理学[M].北京：高等教育出版社，2008.