嵌入灰度级信息的粗糙模糊熵阈值分割法

张 干，吴成茂

（西安邮电大学 电子工程学院，陕西 西安710121）

0 引 言

目前常用的图像分割方法可分为3类：基于边缘检测的方法，基于区域的方法，以及阈值化分割方法。其中阈值分割是应用最为广泛的一种图像分割方法［1，2］。图像的分割质量是由人来做主观评价的，而图像在本质上具有模糊性，如三维物体投影为二维图像时有信息损失；纹理、边缘、区域等的定义具有模糊性；对图像底层处理的解释有模糊性［3］，近年来模糊集和粗糙集阈值分割技术在图像分割中的应用日益广泛［4，5］。

基于粗糙集理论的优势，Debashis Sen 和Sankar K.Pal提出使用粗糙集和模糊集结合的方法进行图像处理［5］。本文在粗糙模糊集基础上提出一种灰度级融合粗糙模糊熵阈值分割法。相比于信息熵图像分割方法在去噪和保留图像细节信息时的局限性，融合灰度级概率的粗糙模糊熵算法更符合图像直方图特点，仿真实验对其分割结果进行了验证。

1 粗糙模糊集基础理论

模糊集和粗糙集理论在处理不确定性和不精确性问题方面推广了经典集合论。法国学者D.Dubofs和H.Prade于1992年提出粗糙模糊集理论，很好地实现了模糊集和粗糙集的融合问题［6］。

1.1 论域中集合的粗糙性

设U 代表论域，X 是U 中任意的一个有特殊属性的集合，R 是论域U 中一个不确定的二元关系，将论域U 分为若干个大小相等的粒度［7］。一个论域中不确定的关系是指论域中的每个元素和这个论域中的其它元素有相似性。通过二元关系R 获取的所有的粒度表示为U／R。论域U 中不可辨别的关系在不同的元素和不同的集合之间用一个不确定的集合X 定义。集合X 可以被两个确定的集合X 和X 近似表示

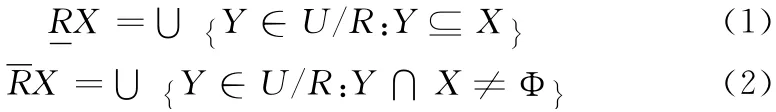
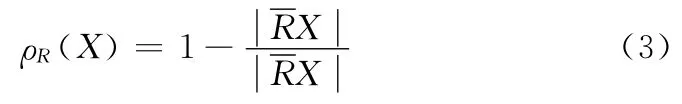
1.2 粗糙模糊集定义

设（U，R）为Pawlak近似空间，U／R ＝｛X1，X2，…Xn｝是U 上由R 导出的所有等价类，模糊集B 在U 中的上、下近似分别记为，且被定义为U／R ＝｛X1，X2，…Xn｝上的模糊集，B：U／R →［0，1］，使得

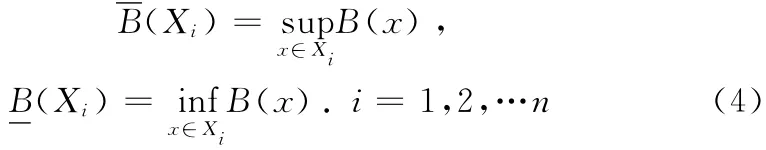
2 图像粗糙模糊集描述

对于一幅有L 个灰度级大小为S1×S2的图像I，用Λ代表L 个灰度级组成的论域，其中的元素表示为li，i＝1，2，…L。

2.1 图像灰度级的粗糙集表示

首先定义两个互斥的集合Ab和Bb，分别代表论域Λ中 “明亮”和 “灰暗”两个区域，如下

根据上定义可以得到：Ab∪Bb＝Λ.灰度值b被称作交叉点或阈值。

因为相邻灰度值的视觉相似性，我们对论域Λ进行粒度计算。如图1所示，ω代表粒度大小，文献 ［7］中方法，粒度分割使阈值b从不在任何一个粒度的边界，由于Λ 内子集有限的分辨能力，使用粗糙集理论获取Ab和Bb的下近似

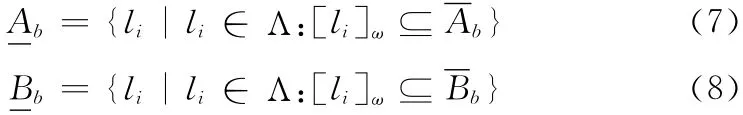
Ab和Bb的上近似定义为

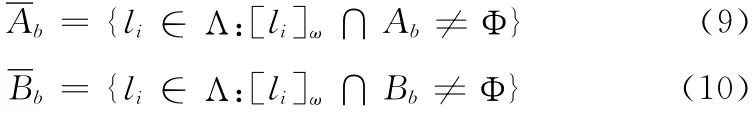
其中，［li］ω代表大小为ω包含像素li的粒度。现在两个粗糙集，［Ab，Ab］代表Λ中的灰度级“明亮”区域，［Bb，Bb］代表Λ中灰度级“灰暗”区域。［Bb，Bb］的定义如图1所示。

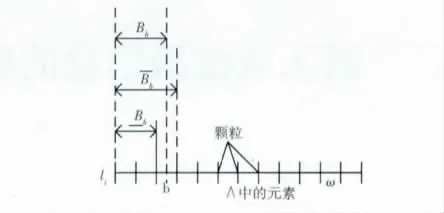
图1 图像灰度值的粗糙集

2.2 灰度级中的粗糙模糊集

在式 （5）和式 （6）中，子集Ab和Bb都是分明集，如第一节所述，图像中不同区域之间有着 “模糊”的边界，因此，将Ab和Bb变为模糊集比分明集的效果好。定义两个模糊集合Ab和Bb，分别代表Λ 中 “明亮”和 “灰暗”的灰度级，如下

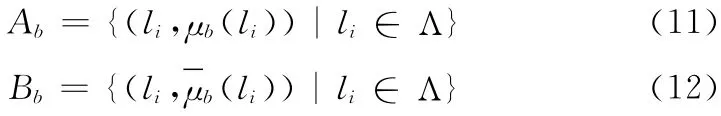
其中，μb（li）＝1－μb（li）。根据定义容易得出Ab∪FBb＝Λ，其中∪F代表模糊集合的并，Λ 中每个元素的隶属度函数之和为1。使用S函数［9］来计算μb（li）

其中，0＜a＜b＜c＜L－1，灰度值b受参数a，c的制约，一般选取b＝（a＋c）／2，Δb ＝b－a＝c－b是构成模糊集合的带宽。

由于在图像中灰度级直觉分辨的相似性，论域Λ 中子集的分辨能力有限，使用粗糙集理论得到模糊集Ab和Bb的下近似定义

其中

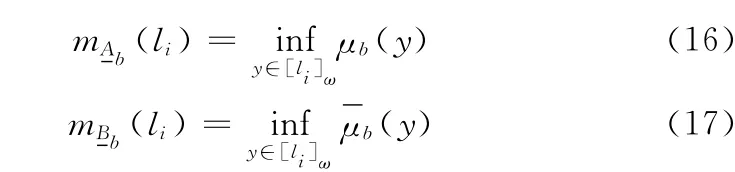
相对应的上近似为

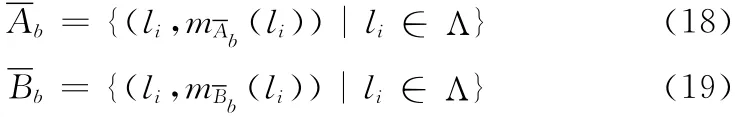
其中

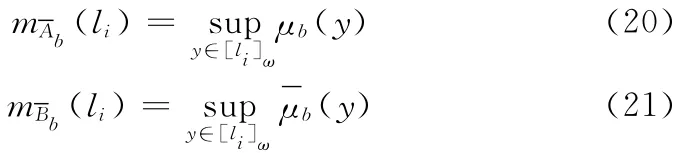
其中，［li］ω是包含元素li的的大小为ω 的颗粒，特别的上近似和下近似是Ab和Bb被近似的模糊集合。

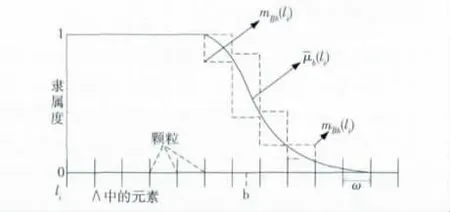
图2 图像灰度的粗糙模糊集

3 图像信息的不确定性度量

图像成像是一个由三维到二维的过程，使得图像本身具有许多不确定性，人的视觉对于图像中的灰度级是模糊的，所有这些不确定性都增加了图像分割的复杂性。

图像信息中的不确定性可以概括为灰度的不确定性和空间的不确定性。图像信息的不确定性度量方法有模糊熵度量法，粗糙熵度量法，以及模糊集和粗糙集相结合的度量方法。本文采用粗糙模糊熵度量方法度量图像信息的不确定性。

3.1 粗糙和粗糙模糊熵

本节依据上述粗糙模糊熵理论度量图像的模糊程度。

上节在一幅图像中，已经根据分明区域得到一组粗糙集，根据模糊区域得到一组粗糙模糊集。并且在两个集合中分别指定了［Ab］和［Bb］。

论域Λ 中的粗糙度度量如下

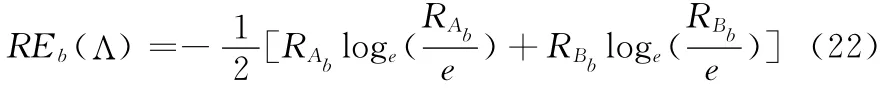
其中

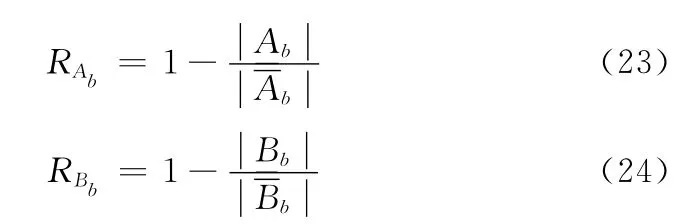
REb的取值范围是［0，1］，仅当RAb＝RBb＝0时REb取到最小值0，仅当RAb＝RBb＝1时REb取到最大值1。这也和熵最大时信息的不确定性最大理论保持了一致。在RAb＝RBb时，REb的取值如图3所示。

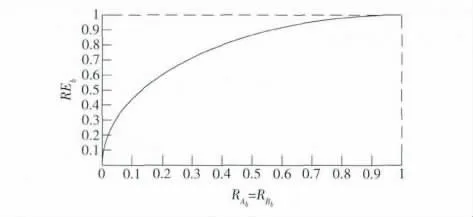
图3 粗糙模糊集隶属度RAb ＝RBb

3.2 图像不确定量计算方法

设集合X 是图像I 中一个子集，其中包含N 个元素分别为xn，n＝1，2，…N 。用HX（li）表示在集合X 中灰度值为li的元素的个数，用下式定义集合X 中的粗糙模糊度度量方式［11］

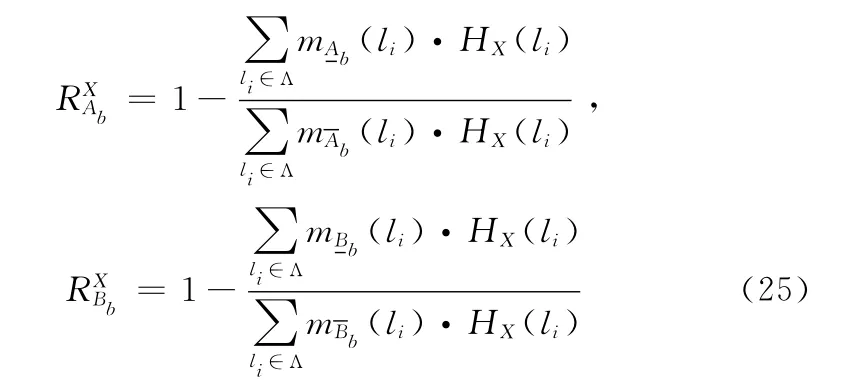
结合粗糙熵得到集合X 中的粗糙模糊熵度测量式

图4是集合X 被粒度划分后，不同灰度级的元素个数示意图。

图4 灰度直方图中不同灰度级粒度

定义集合X 中的粗糙熵度量之后，式（25）即可简化为

4 灰度级融合粗糙模糊熵

针对式 （26）中粗糙模糊熵在对目标和背景区分模糊，含有噪声的图像分割不明显的问题，引申出灰度级融合粗糙模糊熵阈值算法，该方法在原最大模糊熵算法基础上，增加模糊隶属函数参数所对应的灰度级大小信息的变权参数，表达式描述为

其中，0＜a＜b＜c＜L－1，且a，c选取不同的灰度级大小的模糊隶属函数参数。在实际应用中，针对不同类型图像，可以选取适当α值，使REXa，c（Λ）取值最大化，获取最佳参数a，c，以便获得满意的分割效果。即

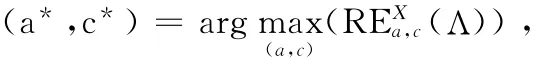
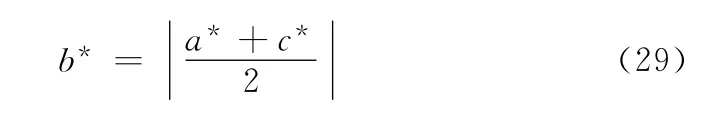
根据分割阈值b＊对原图像进行二值化处理，二值化函数通常表示为

5 实验结果及分析

为了验证本文所建议的图像分割方法的有效性，采用一些典型图片进行了分割测试，其实验结果如图5－图8所示。其中图5，图6中的两幅图片的分割结果都是突出图像中 “明亮”区域部分，对分割要求有较好的去除噪音效果；在该组实验中，参数α＝2。图7，图8中的两幅图片的分割结果对图像中 “灰暗”部分的细节信息的保留要求较高，该组实验中参数α＝－0.5。

从图5至图8所示的灰度图像分割结果来看，嵌入灰度级信息的粗糙模糊熵相对传统信息熵和粗糙模糊熵阈值法能获得更好的分割效果，其分割结果目标信息更加全面，噪声少且图像细节信息较为丰富。因此，本文所建议的融入灰度级信息的粗糙模糊熵阈值法是有效的。

6 结束语

针对光照不均匀灰度图像难以分割的问题，提出融合灰度级大小信息的粗糙模糊熵分割法，不仅考虑灰度级概率信息和大小信息，而且考虑了灰度级的模糊信息和粗糙性所对应的粗糙模糊不确定性，相比现有的仅利用灰度级概率的随机不确定性、粗糙模糊不确定性的分割方法能获得更加满意的分割结果。该改进分割方法有利于光照不均匀图像分割的实际需要。

［1］ZHANG Yujin.Image engineering ［M］.Beijing：Tsinghua University Press，2013：73－74 （in Chinese）.［章毓晋.图像工程 ［M］.北京：清华大学出版社，2013：73－74.］

［2］Rafael C Gonzalez，Richard E Woods.Digital image processing［M］.3rd ed.Prentice Hall，2007：711－712.

［3］WU Chengmao.Image segmentation based on subset hood measure theory ［J］.Pattern Recognition and Artificial Intelligence，2007，20 （6）：805－813 （in Chinese）.［吴成茂.一种基于包含度理论的图像分割方法 ［J］.模式识别与人工智能，2007，20 （6）：805－813.］

［4］ZHAO Feng.Research on several image segmentation methods based on fuzzy entropy theory ［D］.Xi'an：Xi'an Institute of Posts and Telecommunications，2007：19－23 （in Chinese）.［赵凤.基于模糊熵理论的若干图象分割方法研究 ［D］.西安：西安邮电学院，2007：19－23.］

［5］Debashis Sen，Sankar K Pal.Generalized rough sets，entropy，and image ambiguity measures［J］.IEEE Transactions on Systems，Man，and Cybernetics，2009，39 （1）：117－128.

［6］MEI Yuling.Research on theory and application of type－2fuzzy rough sets ［D］.Harbin：Harbin Engineering University，2009：5－8 （in Chinese）.［梅玉玲.二型模糊粗糙集的理论及应用研究 ［D］.哈尔滨：哈尔滨工程大学，2009：5－8.］

［7］Sen D，Pal S K.Histogram thresholding using beam theory and ambiguity measures ［J］.Fundamental Informaticae，2007，75 （1）：483－504.

［8］LI Xuewen，WEI Lili.The roughness measure of rough－fuzzy sets ［J］.Journal of Guizhou Normal University （Natural Sciences），2007，25 （1）：68－71 （in Chinese）. ［李学文，魏立力.粗糙模糊集的粗糙性度量 ［J］.贵州师范大学学报 （自然科学版），2007，25 （1）：68－71.］

［9］Sen D，Pal S K.Histogram thresholding using fuzzy and rough measures of association error［J］.IEEE Transactions on Image Processing，2009，18 （4）：879－888.

［10］WU Runmin.Fuzzy－rough method of measurement ［D］.Chengdu：Southwest Jiaotong University，2010：8－10 （in Chinese）.［吴润民.粗糙模糊性的度量方法研究 ［D］.成都：西南交通大学，2010：8－10.］

［11］Debashis Sen，Sankar K Pal.Measuring ambiguities in images using rough and fuzzy set theory ［C］／／IEEE International Conference on Signal processing，Communications and Networking，2008：333－338.