牛顿插值与分块算法对自适应支持度的研究

周兴斌，骆四毛

（南昌大学 信息工程学院 计算机中心，江西 南昌330031）

0 引 言

为获取数据之间隐藏的关系或者规律，人们在数据挖掘领域方面进行了不断的努力探索与研究，而在1994 年，R.Aglawal等人在他们的AIS 算法基础上提出了Apriori算法［1］。该算法便进一步地促进了人们在数据挖掘方面的研究工作，但其也仍含有不足之处，如在该算法的第一步中，频集所需要的计算等开销远大于规则所需要的计算等开销，这使得频集挖掘成为关联规则挖掘的关键［2，3］，而频集挖掘的关键是最小支持度阀值的确定。因此，本文针对如何能很好适应其事务数据库的最小支持度确定等问题进行了探讨，即自适应最小支持度。根据已查阅的文献资料显示，目前，许多研究学者等已通过利用牛顿插值算法对自适应支持度进行了研究，这使得关联规则挖掘的结果更加精确，但该项研究也仍然存在着许多的不足，如过高的数据扫描量导致过高的时间复杂度和因点值误差导致的凸点问题等。而为有效解决高时间复杂度和凸点问题，本文分别通过结合分块算法和哈希表中处理冲突的方法思想进行了探讨，并通过在电子商务应用系统中的运行情况来验证该解决方案的可行性，以期最终增强支持度阀值的自适应性。

1 理论简介

Apriori算法思想是通过利用已经预先设置的最小支持度挖掘出符合要求的频集，然后再通过也已经预先设置的最小置信度来挖掘出关联规则［4］，而下文便通过利用形式化描述语言对关联规则的相关基本概念进行了清晰地阐述。

假设R ＝｛r0，r1，r2，…，ri，…，rm｝，即R 是由m 个不同数据项组成的集合，其中的ri元素称为项，而由m 个项组成的集合称为m－项集。另外，若有一个事务数据库P，一般地，则表中的每条记录代表了一个事务T，每个事务T 都含有唯一标识符ID，且每条记录中的每个属性字段 （具体含义或是一个产品的代表标号，或是某个产品的一个基本属性）作为一个项，因此事务也是由许多项组成的集合，且是项集R 的子集，即T R。

定义1 （求规则）：若有一频集H，找出其中的所有非空子集h，得出的规则则为h→H－h，即作为规则的前件和后件的子集交集为空，且该规则在P 中具有一定水平的支持度sup和置信度conf。

定义2 （支持度）：在P 中，若有一项集F，包含该项集的事务数为N，总事务数为M，则支持该项集的支持度为 （N／M）。而若一条规则W →Q，支持W ∪Q 的事务数是U，则整条规则的支持度是 （U／M）。

定义3 （置信度）：在P中，若有一条规则W →Q，支持W 的事务数为N，而在支持W 的事务数中同时支持Q的事务数是L，则该规则的置信度是 （L／N）。

定义4 （关联规则）：从P 中挖掘出规则实质上便是要求挖掘出同时大于或等于最小支持度和最小置信度的规则，即强规则，又称为关联规则。

定义5 （自我连接）：若有一频集HK，生成Hk＋1的步骤名为自我连接，即只要保证某个项集的前K 项相同，只有最后一项不同即可连接生成新的k＋1项集，形式上描述为若X＝ ｛x0，x1，x2，…，xi，…，xk，xk＋1｝，Y＝｛y0，y1，y2，…，yi，…，yk，yk＋1｝，且满足x0＝y0，x1＝y1，x2＝y2，…，xi＝yi，…，xk＝yk，xk＋1 ＜yk＋1 （表示最后两项不相同）。

定义6 （剪枝规则）：对由频集Hk新生成的k＋1－项集进行剪枝时，只要k＋1项集中有任何一个子集不在频集Hk中就可丢弃，不加入候选集Ck＋1中。

由以上定义易知，从数学角度分析，关联规则实质上是一种项集之间的蕴含关系。同时，从所代表的实际意义角度分析，支持度是对关联规则在某事务数据库中重要性的衡量，表明该规则出现的频率，而置信度是对关联规则在某事务数据库中准确度的衡量，表示规则的强度。此外，项集中包含项的个数称为项集长度。

2 算法改进及性能分析

在挖掘关联规则时，如果支持度［5，6］被设置得过高，则稀有规则很容易被泄露，知识覆盖面窄小，导致偏颇的决策产生，而如果其被设置得过低，则规则数过多，冗余度偏高，即产生组合爆炸，易导致决策无重点，不利于其优势的发挥。所以，针对支持度在自适应时所产生的过高时间复杂度问题，本章提出了一种改进的方法，即牛顿插值法和分块算法进行结合。

该改进算法的主要思想是算法首先对事物数据库进行分块挖掘［7］和自主经验学习，根据每块形成的点值，运用牛顿插值算法重新确定最小支持度阀值，之后以整个事物数据库为目标对象进行关联规则的挖掘。其中，每块的大小取占整个事务数据库的百分比来确定。之后，系统自动确定每块的实际大小。另外，期望的规则数N （块规则数）也需根据用户的一定经验来设定，或者采取默认方式，即其取值为各个块所挖掘出规则数的平均值。当不分块时，每次牛顿插值算法对整体事物数据库的挖掘相当于对一子集事物块进行挖掘。每一块也需要确定各不相同的最小支持度，每块最小支持度确定的方式可以是根据初始设定的支持度以微小增幅进行线性改变 （如每次增加1个单位）。同时，在实验过程中，系统自动记录下对每块所挖掘出的关联规则数。根据牛顿插值公式［8，9］

其中，C、n、M 分别为置信度、规则条数、事务集的最大属性个数。为减少可变因子和有重点性的研究本算法在支持度自适应方面的性能，大写字母在本算法中表示为固定值，且每一块形成一个点值坐标，即 （C＊n／M，sup）。之后，改进后的算法再调用牛顿插值算法求取出含X 的多项式。在本文中，X＝C＊N／M，并被代入已求取出的X 多项式中。于是，该改进后的算法获取到自适应的支持度SUP。最后，新的Apriori算法根据SUP 进行关联规则的挖掘，增强了其自我快速学习的能力。

此外，因在利用牛顿插值算法时用来确定X 多项式的点值偏差可能会使该算法产生凸点问题，即该问题会使牛顿插值算法产生异常点，不利于实验的正常进行及观察。针对该问题，本文通过充分借用哈希表中处理冲突方法的思想［10，11］来解决。具体而言，为让原本用来确定关于X 多项式的初始点值在求取差分商时不致使牛顿插值算法出现凸点，本文采用线性函数对点值进行误差修正，即如果初始点值数组中含有相同值，则运用以下函数进行修正，并编写了相应的修正算法

其中，根据挖掘经验和相对误差修正的幅度，在本文中，a＝1，b＝2。实验证明，该问题被得到了良好的解决，算法运行流畅，数据处理的平滑性更强，从而使算法挖掘出的结果更加精确。以下是具体的改进过程，且用伪代码进行示意。

算法名称：Apriori＿newton

输入：P－事务数据库；min＿sup－初始最小支持度；期望规则数N；块大小占比subsetLen （不分块时为挖掘次数，分块时为块的个数）

输出：H－P中的频集

方法：

判断各值是否有相同，若相同，运用函数 （2）进行误差修正 （据挖掘经验，2属误差可控范围）；

针对pointMap，根据差分和差商思想，形成关于X的多项式时；

代入X 值取得更佳支持度值；

3 实验数据来源及结果分析

3.1 实验数据来源

本系统所用数据主要是通过采用购物系统所产生的实际数据，生成的数据量规模为10万以上。其数据所存放的数据库是Mysql。

3.2 实验结果分析

通过对有关电子商务应用系统的开发，本节附表1和图1所示分别为实验结果对比数据表和实验数据分析结果曲线图 （采用Fushion Charts编码自动绘制）。

表1 对同级事务集分块或次数不同实验结果数据

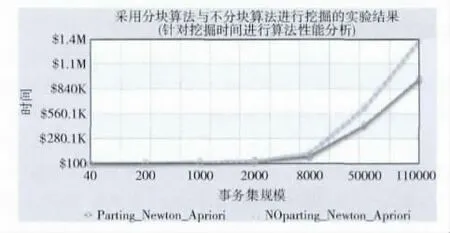
图1 对异级事务集分块或次数同实验结果分析

在对本节中的上述附图作出分析之前，本文需要说明的是，在运行分块时的算法时，实验结果中的规则数是262条，而在运行不分块时的算法时，实验结果中的规则数是267条 （限于篇幅，结果图未列出），两种算法所得出的实验结果误差为5，且其有262条规则相同。实验表明，改进后算法只遗漏了5 条规则，且该5 条规则为冗余性规则，这表明了该误差是属于可控范围的，所提出的改进方案是可行的。以下便是针对上述附图中的实验结果分别作出相应的数据分析或性能解析。

在表1中，为利于对比每次实验效果，本文通过针对相同级别规模下的 （事务数＝1000条）事务数据库进行挖掘，设置了不同的分块数或次数，并分别对算法运行时间和自适应最小支持事务数作了记录 （为便于观察，本文采用最小支持事务数来分析实验结果。事实上，最小支持度＝最小支持事务数／总事务数）。通过对表中数据进行观察并发现，当被挖掘出的结果所含有的误差不是很大时，系统采用分块算法时分块的数目越多，运行时间趋少，而其采用不分块算法时运行的次数越多，运行的时间趋多。同时，随着点值数增多，分块时算法运行时间比不分块时算法运行时间要更少，并前后两者的时间差值趋大。

在图1中，在块数或次数相同 （取值为2）的情况下，本文设置了不同级别规模的事务数据库，并分别对算法运行时间和新的自适应最小支持事务数作了记录。其中，虚线代表了不分块时牛顿插值算法与Apriori算法的结合方案，即图1中标明为NOparting＿Newton＿Apriori（NOPNA）线，而实线代表了分块时牛顿插值算法与Apriori算法的结合方案，即图1中标明为Parting＿Newton＿Apriori（PNA）。通过对图1中两线走势及其间距进行观察并发现，PNA 线始终处于NOPNA 线之下，且随着事务数的不断增多 （即事务数据库规模不断增大），两线所代表的方案所需用的挖掘时间都分别趋增，当事务数小于8000条时，其增速较缓，当事务数大于8000条时，其增速陡快。同时，当事务数小于8000 时，两线间距不明显，而当事务数大于8000时，两线间距明显，并趋大，这说明了在事务数据库规模比较大时，分块时算法比不分块时算法具有比较大的优势，适合于对实时性或数据量大等要求较高的情况，而在事务数据库规模比较小时，仅从时间复杂度角度上而言，PNA 和NOPNA 算法两者间无较大明显区别，两者一般可以互为换用。

综上所述，Apriori算法的改进方案比其现有的方案更加高效，尤其是在面对事务数据库规模比较大时，该改进方案的优势更加突出，更加明显。同时，对于牛顿插值算法中的凸点问题，通过系统的多次正常执行及测试，这说明该凸点问题已得到较好的解决。这些改进措施所带来的优势也因此能在一定程度上满足用户的实时性要求，从而用户的满意度及其相关的收益能力被得到了有效的提高，达到了预期目标。

4 结束语

针对自适应支持度等问题，通过分块算法和哈希表冲突处理方法思想的运用，本文有效的降低了过高的时间复杂度水平和有力的解决了牛顿插值算法中的凸点问题。实验证明，在挖掘出的结果偏差属于允许的误差范围之内时，该新方法在某方面是有效的，可行的，而且关联规则挖掘的时间得到了较大程度的缩短，挖掘结果的精度也在一定程度上得到了提高，从而增强了支持度的快速自适应性能力。但该方案中仍然有如下几个方面的不足：第一，在表1中，随着在分块时分块数的增多，虽然改进后算法的挖掘时间不断得到缩短，但新自适应最小支持事务数不稳定，其取值的抖动幅度偏大，而不分块时其取值则较为稳定；第二，在图1中，PNA 线斜率仍然偏高，其时间增速仍然较快，PNA 线代表的算法在时间复杂度方面仍有很大的改善空间；第三，初始最小支持度、每块支持度增幅及期望规则数等如何进行更好的设置，以便契合实时性要求及环境；第四，为使牛顿插值算法在处理数据时更加平滑，异常数据的检测方法［12］或误差修正函数的选择有待进一步的探讨。总之，为将系统设计为一个能够快速响应、决策准确等高要求的电子商务［13］应用系统，相关的工作步伐仍将有序而坚定的行进下去。

［1］LIU Huating，GUO Renxiang，JIANG Hao.Research and improvement of Apriori algorithm form in ing association rules［J］.Computer Applications and Software，2009，26 （1）：146－149 （in Chinese）.［刘华婷，郭仁祥，姜浩.关联规则挖掘Apriori算法的研究与改进 ［J］.计算机应用与软件，2009，26 （1）：146－149.］

［2］LI Yanwei，DAI Yueming，WANG Jinxin.Improved algorithm for mining weighted frequent itemsets［J］.Computer Engineering and Applications，2011，47 （15）：165－167 （in Chinese）.［李彦伟，戴月明，王金鑫.一种挖掘加权频繁项集的改进算法 ［J］.计算机工程与应用，2011，47 （15）：165－167.］

［3］LIU Jingchao，GENG Boying，SONG Shengfeng.Mining weighted frequent items in intrusion detection ［J］.Computer Engineering and Design，2008，29 （8）：1961－1962 （in Chinese）.［柳景超，耿伯英，宋胜锋.入侵检测中加权频繁项集挖掘 ［J］.计算机工程与设计，2008，29 （8）：1961－1962.］

［4］QIAN Xuezhong，KONG Fang.Research of improved Apriori algorithm in mining association rules ［J］.Computer Engineering and Applications，2008，44 （17）：138－140 （in Chinese）.［钱雪忠，孔芳.关联规则挖掘中对Apriori算法的研究 ［J］.计算机工程与应用，2008，44 （17）：138－140.］

［5］SHEN Yaping，ZHENG Cheng.Efficient strategy to obtain support in multi－database［J］.Computer Engineering and Design，2008.12，29 （23）：6037－6038 （in Chinese）.［沈亚萍，郑诚.在多数据库中确定支持度的有效方法 ［J］.计算机工程与设计，2008.12，29 （23）：6037－6038.］

［6］ZHANG Chunsheng，SONG Linlin.Sub－support Apriori algorithm and its application ［J］.Computer Engineering and Applications，2010，46 （16）：157－159 （in Chinese）.［张春生，宋琳琳.分段支持度Apriori算法及应用 ［J］.计算机工程与应用，2010，46 （16）：157－159.］

［7］GAO Le，ZHANG Jian，TIAN Xianzhong.Improvement and implementation of VIPS algorithm ［J］.Computer System and Applications，2009 （4）：65－69 （in Chinese）. ［高乐，张健，田贤忠.基于视觉的Web 页面分块算法的改进与实现 ［J］.计算机系统应用，2009 （4）：65－69.］

［8］FU Xiang，GUO Baolong.Overview of image interpolation technology［J］.Computer Engineering and Design，2009，30（1）：141－143 （in Chinese）.［符祥，郭宝龙.图像插值技术综述 ［J］.计算机工程与设计，2009，30 （1）：141－143.］

［9］LIN Zhixian，YANG Wenchao，GUO Tailiang.A field emission display zooming system based on the improved Newton algorithm ［J］.Journal of Optoelectronics·Laser，2012，23 （5）：844－848 （in Chinese）. ［林志贤，杨文超，郭太良.基于改进型Newton算法的场致发射显示器缩放系统研究 ［J］.光电子·激光，2012，23 （5）：844－848.］

［10］XIE Yun.HCAA：A hash collision excessive dynamic solution algorithm ［J］.Computer Applications and Software，2011，28 （11）：145－149 （in Chinese）.［谢云.HCAA：一种哈希冲突过度的动态解决算法 ［J］.计算机应用与软件，2011，28 （11）：145－149.］

［11］ZHANG Zhaoxia，LIU Yaojun.Effective solution to Hash collision［J］.Journal of Computer Applications，2010，30 （11）：2965－2966 （in Chinese）.［张朝霞，刘耀军.有效的哈希冲突解决办法［J］.计算机应用，2010，30 （11）：2965－2966.］

［12］WANG Yuanming，XIONG Wei.Outlier detection methods in data analysis［J］.Journal of Chongqing Institute of Technology （Natural Science），2009，23 （2）：86－89 （in Chinese）.［王元明，熊伟.异常数据的检测方法 ［J］.重庆工学院学报（自然科学），2009，23 （2）：86－89.］

［13］QU Zhenggeng，TANG Xiaoqin.Research of data mining technology based on electronic commerce ［J］.Electronic Design Engineering，2009，17 （3）：37－39 （in Chinese）.［屈正庚，唐晓琴.基于电子商务中的数据挖掘技术研究 ［J］.电子设计工程，2009，17 （3）：37－39.］