基于二分法的双馈风力发电机组功率协调控制策略研究

刘力卿，兰立雄，向安韡，任 惠

(1.华北电力大学新能源电力系统国家重点实验室，河北保定071000;2.福州市电力公司，福建福州350000)

0 引言

随着风力发电的快速发展，风力发电技术不断成熟，风力发电比例逐渐增大。但由于风电场功率输出具有随机性、波动性和间歇性等特点，严重影响电网的安全稳定运行。因此，各个国家制定的风电场并网规则都对风电场的有功输出调控能力作了要求。文献［1～2］对各个国家风电场接入电力系统的控制方法进行了研究，发现各个国家对风电场的控制要求不尽相同，但都要求风电场具备有功功率的主动控制能力。我国国家电网公司制定的《风电场接入电网技术规定》［3］明确要求并网风电场必须具备有功功率的主动调控能力，以满足电网调度要求。

变速恒频双馈风力发电机组是目前风电市场上的主流机型。文献［4～7］结合风电场功率预测技术，研究了双馈型风电场内风电机组的有功控制策略，均取得了较好的控制效果。但是这些文章都是研究如何将风电场的有功功率调控目标分配到单台机组，而对单台风力发电机组如何实现分配的功率控制目标没有进行详细研究。双馈风力发电机组能够通过调整转速和桨距角控制机组的有功输出。文献［8～14］对双馈风电机组的有功控制方式进行了研究，通过对双馈风电机组转速和桨距角的控制，均可起到调整风电机组有功输出的作用，但是都没有对转速和变桨距之间的协调控制策略进行研究。文献［15，16］通过协调控制风电机组的转速和桨距角控制机组的频率，为本文的研究提供了重要的借鉴意义。

为了提高双馈风力发电机组(Doubly-fed Induction Generator，DFIG)有功输出的主动控制能力，本文结合变桨距控制和转速控制各自的优点，提出基于二分法的有功功率分层协调控制策略。该控制策略以变桨距控制作为外层控制，对机组输出功率进行粗调;在变桨距控制基础上，以转速控制作为内层控制，利用二分法确定机组在对应桨距角下的最优转速，对机组输出功率进行微调。本文所提控制策略容易实现，能够对机组输出功率进行快速准确调整。

1 双馈风电机组的有功功率关系

双馈风力发电机组是由风力机、双馈发电机、交直交变频器等构成。风力机从风能中捕获能量，将之转变为机械能。机械能由传动系统传递到发电机，发电机将机械能转换为电能输送到电网中。发电机的定子直接与电网相连，转子通过交直交变频器与电网相连。交直交变频器由两个背靠背连接的电压型PWM 变频器构成:靠近双馈电机转子一侧的变频器称为转子侧变频器，靠近电网侧的变频器称为网侧变频器。网侧变频器一般运行在高功率因数整流模式，为转子侧变频器提供恒定的直流母线电压;转子侧变频器通过控制转子励磁电流，实现双馈电机的变速恒频运行［17～19］。双馈电机变速恒频发电系统的功率关系如图1所示。

图中，Pm为风力机输入的机械功率;Ps，Qs为发电机定子发出的有功和无功功率;Pr，Qr为从电网回馈到变频器的有功和无功功率;Pg，Qg为双馈电机流入电网的有功和无功功率;Pc，Qc为转子侧变频器输入到发电机转子的有功和无功功率。

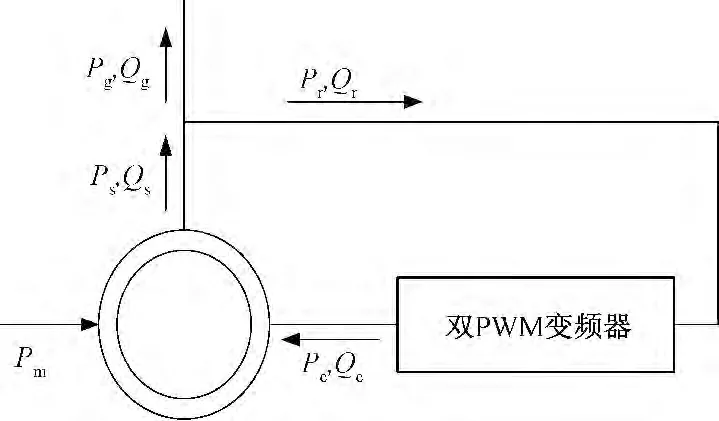
图1 双馈电机变速恒频发电系统的功率关系Fig.1 Power relationships of DFIG variable speed constant frequency wind power system

忽略发电机的绕组损耗、变频器的开关损耗以及线路损耗，双馈风电机组的功率关系可表示为

式中:Pm为风力机传给发电机的机械功率;ρ 为空气密度;R 为风力机叶轮半径;vw为风速;λ为叶尖速比;β 为桨距角;ωm为风力机的转速;Cp为风力机的风能利用系数，Cp是λ与β 的函数，对应关系如图2所示。

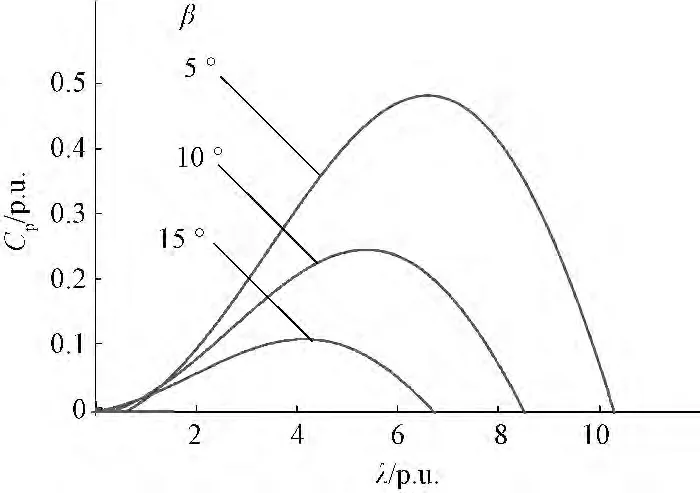
图2 CP与λ和β 的关系图Fig.2 Relationship between CP，λand β

2 双馈风电机组的有功功率调控方式

一般地，风速低于额定风速时，双馈风力发电机组通过转速控制，根据风速调节风力发电机组的转速，保持最佳叶尖速比，最大程度地利用风能;风速高于额定风速时，机组的转速不变，通过变桨距控制调节风力机的桨距角，使风力发电机组输出恒定的额定功率。

2.1 转速控制

转速控制主要是通过控制双馈电机的电磁反转矩，调节风力机的转速和叶尖速比，改变风力机的风能利用系数，从而达到调控风力发电机组有功功率的目的［20］。

桨距角固定时，叶尖速比与风能利用系数的对应关系如图3所示:

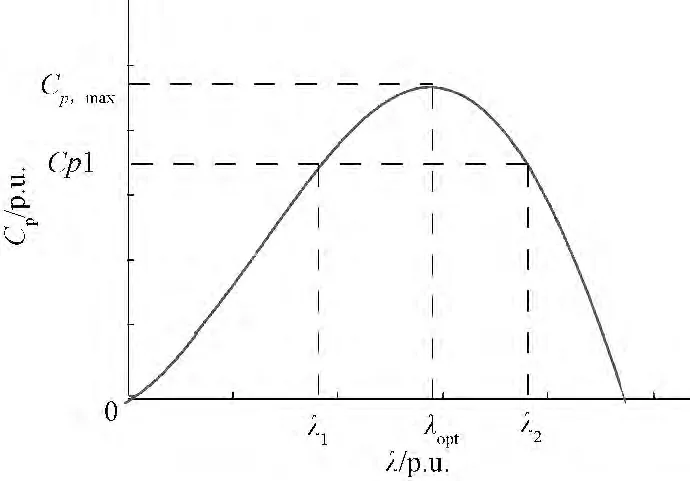
图3 CP与λ的对应关系曲线Fig.3 Relationship between Cp and λ

从图3 可知，风能利用系数随叶尖速比的变化而改变，在最佳叶尖速比时取得最大值，叶尖速比增大或减小，风能利用系数都将减小。因此，当风力机的桨距角确定时，主动调整风力发电机组的叶尖速比就能控制风力发电机组的输出功率。例如，t1时刻，风力发电机组以最佳叶尖速比运行，叶尖速比为λ1，风能利用系数为Cp1，输出功率为Pm1;t2时刻，风速不变，风力发电机组将输出功率主动减发至Pm2，此时的风能利用系数为Cp2，叶尖速比为λ2，由公式(1)可得如下关系:

公式(8)提供了一种计算风力发电机组风能利用系数的方法，结合公式(2)～(3)求出叶尖速比λ2和风力机转速ωm2，从而利用转速控制调整风力发电机组的转速，实现对机组有功功率的控制。

2.2 变桨距控制

变桨距控制是双馈风力发电机组进行功率调控的重要手段。同种风况下，风力机叶片的桨距角不同，叶片的受力情况就不相同，从而风力机从风中捕获的能量也要发生变化。因此，通过调整风力机的桨距角，就能够实现对风力发电机组有功功率输出的主动控制［21］。

3 有功功率分层协调控制策略

双馈风力发电机组的两种功率控制方式都能对机组的有功功率输出进行调控，但是两种控制方式适用的条件不同:转速控制方式能够快速调节发电机的电磁转矩，控制风电机组的转速，控制精度比较高，但是转速的调节能力受转子侧变频器最大允许电流的限制，功率调控范围有限，适用于对机组的有功功率输出进行微调;变桨距控制方式的功率调节范围比较大，但是由于叶片质量比较大，叶片的桨距角不能快速和灵活地调整，而且也不够精确，适用于对机组的有功功率输出进行粗调。在上述分析的基础上，本文提出了基于二分法［22］的风电机组有功功率分层协调控制策略。

3.1 二分法

二分法主要是一种用来求一元非线性方程零点的方法，简单实用，计算量小，计算速度比较快。一般地，对于函数f(x)，如果存在实数c，使f(c)=0，那么x=c 就是函数的零点。二分法的求解步骤:

(1)假定f(x)在区间［x，y］上单调递增，在该区间内找到a，b 两点，f(a)与f(b)异号，则区间(a，b)内一定有零点;

(2)若f((a+b)/2)=0，则(a +b)/2 即为函数的零点;若f((a + b)/2)＜0，则在区间((a +b)/2，b)上存在零点;若f((a+b)/2)＞0，则在区间(a，(a+b)/2)上存在零点;

(3)选取迭代精度值ε，如果满足式|f(x)| ＜ε，计算结束，所求结果即为函数的零点;否则回到第2 步继续计算，直至满足精度要求为止。

3.2 分层协调功率控制

3.2.1 外层控制

外层控制的作用是对风力发电机组的有功功率输出进行粗调，功率调节范围比较大。因此，本文利用变桨距控制作为机组的有功功率输出外层控制方式。

正常情况下，风速低于额定风速时，风力机的桨距角保持为零，风力发电机组运行于最大风能追踪状态;风速高于额定风速时，风力机组的转速保持不变，叶片桨距角随风速变化，维持恒定的输出功率。本文基于风力发电机组的固有特性，通过实验拟合出风电机组在某一特定风速与相应转速下，机组有功输出与桨距角的关系曲线。对上述关系曲线进行拟合，利用拟合得到的公式即可计算出某一风速下功率调控命令所对应的桨距角。

但是风速的变化范围很大，无法在整个风速变化范围上对相应的有功功率和桨距角进行拟合。基于实用原则，本文将风速的变化范围分为n个区间，可取i=1，…，n +1 个风速值，分别为vi(i=1，…，n+1)，并且使切入风速=v1＜…＜vn+1=切出风速，拟合出每一vi所对应的有功功率－桨距角关系曲线。图4 为某2 MW 风力发电机组部分风速下的有功功率与桨距角关系曲线。

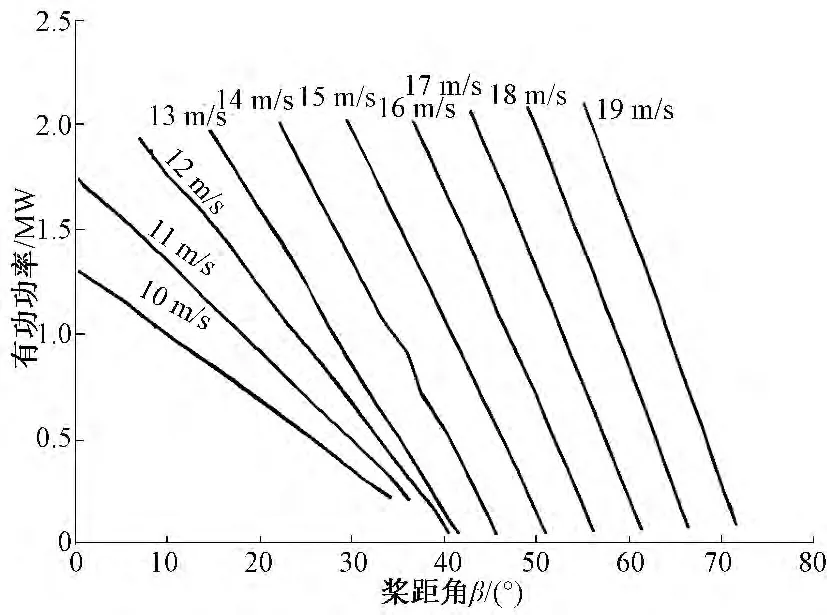
图4 不同风速下有功功率－桨距角关系曲线Fig.4 Corresponding curves of P－β at different wind speed points

根据有功调控命令Pset，在对风力发电机组的功率进行外层控制时，首先根据实际风速vi选择确定风速所处区间［vi，vi+1］，然后按照最小风速vi所对应的有功功率－桨距角关系曲线得出Pset对应的桨距角调控值β1。

3.2.2 内层控制

外层功率控制对风力发电机组的有功功率输出进行了初步调控，但不够精确，还需要对机组的有功功率输出作进一步的控制。本文利用转速控制作为风力发电机组输出功率的内层控制方式，在外层控制基础之上，实现对机组输出功率的精确调控。

桨距角一定时，风能利用系数随叶尖速比的变化而改变，叶尖速比为最佳值时，风能利用系数最大。桨距角变化时，风力机的最佳叶尖速比也发生改变。当实际叶尖速比小于最佳叶尖速比时，风能利用系数与实际叶尖速比之间呈单调递增的函数关系。因此，由前文分析可知，内层控制的关键就是在特定桨距角下求取功率调控指令所对应的风力机实际叶尖速比。

本文利用二分法根据公式(2)和(8)求解风力机的实际叶尖速比λ。分析二分法的计算过程可知，求解的关键就是叶尖速比区间λa，λb以及迭代精度值ε 的选取。本文提出一种分别确定3 个参数的方法:λa代表风力机的最小叶尖速比，风机停机时最小为0，但是无法参与公式运算，因此选取一个较小的正值即可;λb表示能使f(λb)＞0 的值，通过上文分析，利用风机正常运行时的最佳叶尖速比值即可。迭代精度值ε 由电网对风电机组有功功率调控的最小静差确定，通过下式计算可得:

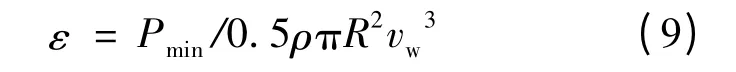
式中:Pmin为有功功率调控的最小静差。利用二分法进行求解，直到得到满意的结果为止，然后求出风力机的转速，通过转矩控制调整风力机的转速，精确调整风力发电机组的输出功率。

综上所述，本文所提风电机组的功率分层协调控制策略控制流程如图5所示。

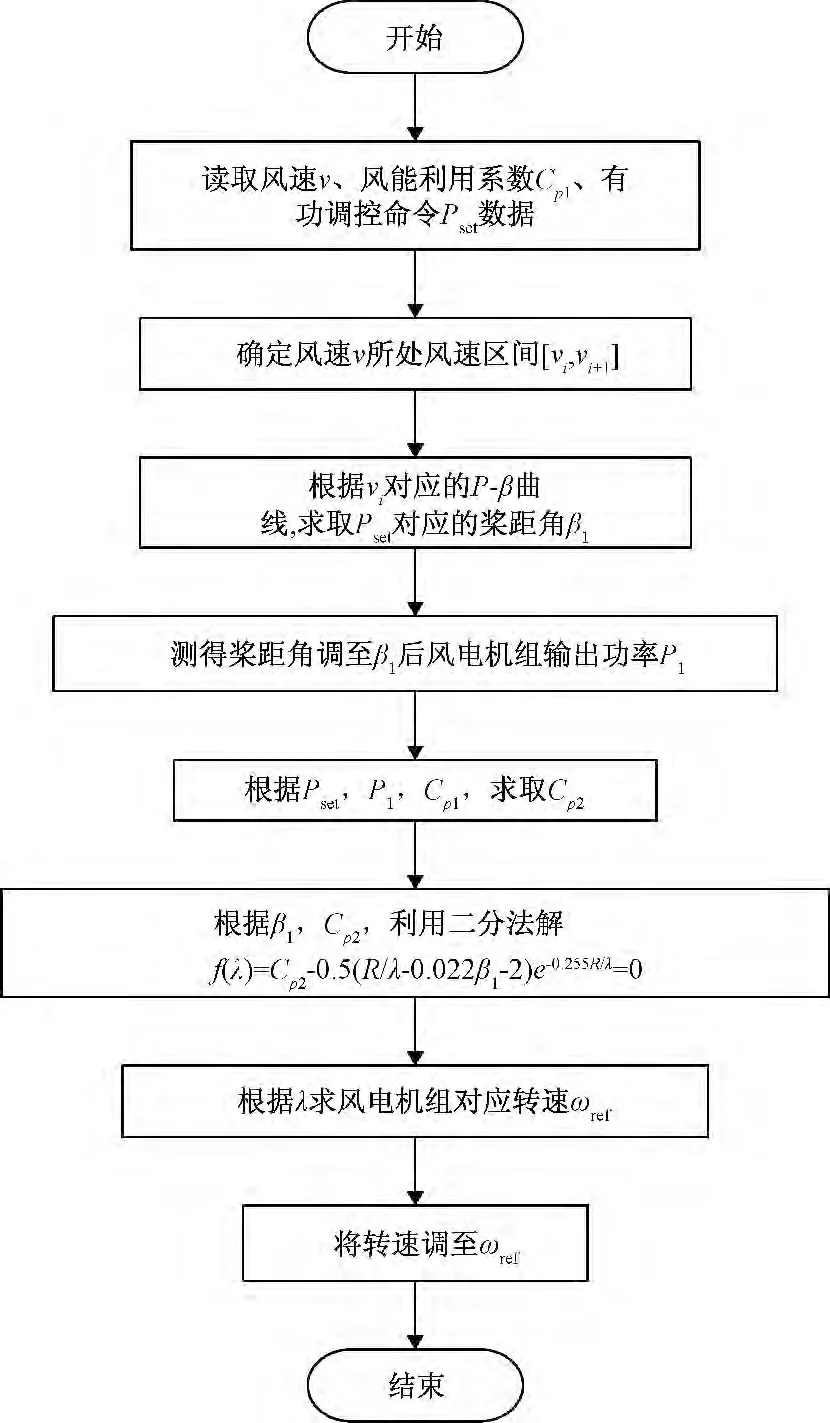
图5 风电机组分层协调功率调控流程图Fig.5 Flowchart of wind turbine power hierarchical coordination control

4 仿真实例

为了验证所提有功功率调控策略的可行性，本文利用PSCAD 仿真平台搭建了一台额定容量为2MW、额定风速为11 m/s 的变速恒频双馈风力发电机组模型，并对具体算例进行了仿真。

仿真实例:风速为10 m/s 时，风力发电机组正常运行，输出功率为1.32 MW;t=1.2 s 时，机组接受功率调控命令，将有功功率输出调控至0.8 MW。

根据本文提出的有功功率分层协调调控策略，首先对机组的输出功率进行外层控制。机组正常运行情况下，风速为10 m/s 时的风力发电机组有功功率与桨距角的对应关系如表1所示。

表1 有功功率与桨距角的对应关系Tab.1 Corresponding relationship between the active power and the pitch angle

表1 中:β 为机组的实际桨距角;Pref为输出功率调控参考值，P 为机组经过功率调控后的实际功率输出，两者不相同的原因主要是由于风力机的非线性引起的。通过查表，应将桨距角主动调整至10.55°，此时机组的实际输出功率为0.98 MW，实现了对机组输出功率的外层控制。

接着，对机组的输出功率进行内层控制。利用二分法求出风速为10 m/s、桨距角为10.55°、输出功率为0.8 MW 时的风力机叶尖速比，确定此时的风力机转速，从而可通过控制电磁转矩调整风力机的转速，完成对机组输出功率的精确调控。仿真结果如图6所示。

仿真结果表明，外层控制通过调整风力机的桨距角实现了风力发电机组输出功率的初步调整，内层控制在外层控制基础之上，通过控制机组的转速，实现了对机组输出功率的精确控制。在内层控制调控过程中，风能利用系数先增大然后逐渐减小，如图6(d)所示，这是因为风力机的桨距角变大，风力机的最佳叶尖速比会相应变小，风力机转速在下降的过程中，叶尖速比先减小至实际桨距角对应的最佳叶尖速比，然后才继续减小到指定的叶尖速比，由此造成机组功率在调控中有少量增大，但这不影响对机组输出功率的精确控制，如图6(e)所示。

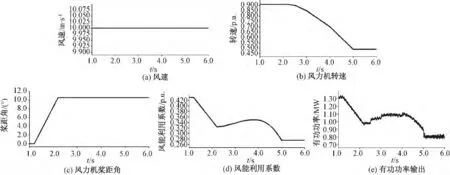
图6 仿真结果Fig.6 Simulation results

5 结论

本文通过分析变速恒频双馈风力发电机组的功率关系以及调控方式，提出了基于二分法的分层协调功率调控策略，并利用仿真验证了所提控制策略的可行性，提高了双馈风电机组的有功功率主动控制能力，为进一步更深入地研究风电场的有功功率调控策略奠定了良好的基础。

［1］Jauch C，Matevosyan J，Ackermann T，et al.International comparison of requirements for connection of wind turbines to power system［J］.Wind Energy，2005，25 (12):27－32.

［2］王伟胜，范高峰，赵海翔.风电场并网技术规定比较及其综合控制系统初探［J］.电网技术，2007，31 (18):73－77.

［3］全国电力监管标准化技术委员会.GB/T 19963－200风电场接入电力系统技术规定［S］.北京:中国标准出版社，2011.

［4］李雪明，行舟，陈振寰，等.大型集群风电有功智能控制系统设计［J］.电力系统及其自动化，2010，34 (17):59－63.

［5］惠晶，顾鑫.大型风电场的集中功率控制策略研究［J］.华东电力，2008，36 (6):57－61.

［6］谢永俊.风电场内有功功率控制研究［D］.北京:华北电力大学，2013.

［7］赵洪山，刘兴杰，李聪.基于机组动态风速信息的风电场有功控制策略［J］.电力科学与工程，2013，29 (1):9－15.

［8］林志明，潘东浩，王贵子.双馈式变速变桨风力发电机组的转矩控制［J］.中国电机工程学报，2009，29 (32):118－124.

［9］潘庭龙，沈艳霞.风电系统滑模极值搜索MPPT 控制方法研究［J］.太阳能学报，2012，33 (12):2193－2197.

［10］陈波，吴政球.基于约束因子限幅控制的双馈感应发电机有功功率平滑控制［J］.中国电机工程学报，2011，31 (27):130－137.

［11］刘云久，王冰，张一鸣.基于风速预测的双馈风力发电机组变桨距协调控制［J］.河海大学学报(自然科学版)，2012，40 (3):357－360.

［12］Tomonobu Senjyu，Ryosei Sakamoto，Naomitsu Urasaki，etc.Output Power Leveling of Wind Turbine Generator for All Operating Regions by Pitch Angle Control［J］.IEEE Transactions on Energy Conversion，2009，21 (2):467－475.

［13］张纯明.大型风力发电机组独立变桨距控制技术研究［D］.沈阳:沈阳工业大学，2011.

［14］秦斌，周浩，杜康，等.基于RBF 网络的风电机组变桨距滑模控制［J］.电工技术学报，2013，28(5):37－41.

［15］张昭遂，孙元章，李国杰，等.超速与变桨协调的双馈风电机组频率控制［J］.电力系统自动化，2011，35 (17):20－25.

［16］张树鑫.双馈风力发电机变桨与变速协调控制［D］.兰州:兰州理工大学，2011.

［17］郎永强，张学广，徐殿国，等.双馈电机风电场无功功率分析及控制策略［J］.中国电机工程学报，2007，27 (9):77－82.

［18］Yufei Tang，Ping Ju，Haibo He.Optimized Control of DFIG-Based Wind Generation Using Sensitivity Analysis and Particle Swarm Optimization［J］.IEEE Transactions on Smart Grid，2009，4 (1):509－520.

［19］Tomonobu Senjyu，Toshiaki Kaneko，Akie Uehara，etc.Output power control for large wind power penetration in small power system［J］.Renewable Energy，2010，34:2334－2443.

［20］谷峰.基于双馈机组风电场的功率控制研究［D］.济南:山东大学，2009.

［21］陈盈今.基于PSCAD 的风电场建模与功率调控研究［D］.保定:华北电力大学，2010.

［22］谢开贵，吴韬，黄莹，等.基于二分法的高压直流输电系统可靠性最优分解［J］.电工技术学报，2010，25 (5):149－154.