基于广域测量系统的潮流转移关键线路快速搜索

徐 岩，郅 静

(华北电力大学电气与电子工程学院，河北保定071003)

0 引言

随着电网规模的不断扩大，潮流转移引起的后备保护过负荷跳闸现象日益突出，成为加速电网连锁故障发展和引发大停电事故的重要原因之一。

电力系统中，因发生扰动或者运行方式改变导致电网的网络拓扑结构发生变化，引起潮流转移，甚至大停电事故的情况可分为两种，一种情况是电网中某线路发生过载，过负荷后备保护动作切除线路，线路断开引起的潮流转移造成其他线路潮流越限，进而导致连锁跳闸;另一种情况是电网中某线路因发生故障被切除，被切除线路上的原有潮流发生转移，导致其他线路过载，引起过负荷后备保护动作切除线路，导致连锁跳闸。以上两种情况都是由于现行的过负荷后备保护装置仅基于就地信息，以单个电力元件为保护对象，不考虑被保护元件切除后潮流转移对其他元件保护带来的影响［1］。

如果能充分利用过负荷后备保护启动到动作的短暂时间，快速准确地搜索到潮流转移的关键线路，对其进行详细分析并采取相应的控制措施，便能有效阻止连锁跳闸以及大停电事故的发生。针对情况1，当电网中某线路发生过载时，在过负荷后备保护动作前，快速准确地搜索到与该线路相对应的潮流转移关键线路，判断过载线路切除是否会导致新的线路过载，如果不会，则允许切除过载线路;如果会，则闭锁保护，并采取紧急控制措施来快速消除过载。针对情况2，某线路因故障断开，其原有潮流发生转移，如果能够在过负荷后备保护启动到动作的短暂时间内搜索到潮流转移的关键线路，并闭锁相应线路的过负荷后备保护，便能有效阻止连锁跳闸。因此，当某线路发生过载或因故障断开时，快速准确地搜索到其相应的潮流转移关键线路，对于维持电网的安全稳定具有重大意义。为叙述方便，本文将情况1 中的过载线路以及情况2 中的故障线路统称为断线线路。

文献［2］从割集的角度出发，将输电断面定义为可以把电力系统分割为互相不连通的两个部分的一组线路，但是没有考虑系统参数。文献［3］根据网络拓扑结构和潮流分布状态对系统进行分区，建立系统状态图寻找输电断面，但容易漏选区内的关键线路。文献［4］根据线路功率组成相似度对线路进行分类，将与断线线路有相似功率组成的线路作为输电断面，但算法比较复杂。文献［5］和文献［6］将线路两侧节点间的最短路径和较短路径作为潮流转移的主要传输路径，但随着电网规模的扩大，该种方法的计算量会显著增大。

基于相量测量单元(Phasor Measurement Unit，PMU)的广域测量系统(Wide Area measurement System，WAMS)可以快速准确获取电力系统的开关状态、节点电压相量、线路电流相量等信息，且高速的数据传输可以使主站的数据更新达到20～50 ms［7，8］，实时刷新电网的网络拓扑结构和潮流分布状态，监测电网的运行情况，当发现系统中有线路发生过载或者因故障被切除时，快速启动本文方法搜索潮流转移关键线路，并为搜索过程提供数据来源。

本文利用WAMS 提供的电力系统实时运行信息，利用图论知识得到断线线路的相关线路集合，确定潮流转移关键线路的搜索范围。采取先缩后扩的搜索模式，由断线线路的并行输电线路出发，先缩小范围，寻找其中与断线线路相角相近且潮流转移电气距离最小的线路构成等相角并行线路;再扩大范围，根据潮流走向寻找等相角并行线路的上游或下游线路。等相角并行线路及其上游或下游线路即为潮流转移关键线路。文中方法简单准确，搜索速度快，在准确率、计算量及电网适应性上有显著优势。仿真算例验证了该算法的有效性和优越性。

1 潮流转移关键线路的搜索思路

在搜索潮流转移关键线路时，首先将搜索范围由全网缩小到相关线路集合;然后采取先缩后扩的搜索模式，利用图1所示的流程逐步得到潮流转移关键线路。

图1 搜索过程Fig.1 Searching process

1.1 并行输电线路和相关线路集合

多次大停电事故的分析结果表明，电力系统中某线路断开后，其潮流会较多地转移到与断线线路有相同电源区或负荷区的线路上［3］。将断线线路的同电源线路和同负荷线路定义为断线线路的并行输电线路。然而，在断线线路断开时，其同电源线路的下游线路和同负荷线路的上游线路也是潮流转移的危险线路。

如图2所示，l1是断线线路，l2是l1的同电源线路，l3是l1的同负荷线路。当l1刚刚断开时，发电机出力和电网所带负荷都没有发生变化，为了保证发电机G1发出的功率能够被送出，l2的功率会增加，同时，为了满足负荷load1的需求，l3的功率也会增加。

l6是l2的下游线路，也就是l1的同电源线路的下游线路，当l2的功率增加时，l6的功率也会增加;l4是l3的上游线路，也就是l1的同负荷线路的上游线路，当l3的功率增加时，l4的功率也可能会增加。

图2 断线线路及其相关线路Fig.2 Broken line and its related lines

因此，本文将断线线路的并行输电线路(同电源线路和同负荷线路)、同电源线路的下游线路和同负荷线路的上游线路都归入其相关线路集合。

1.2 等相角并行线路

将与断线线路相角相近且潮流转移电气距离最小的并行输电线路定义为等相角并行线路。

有功功率由高相角区域流向低相角区域，根据相角的高低可以划分电网潮流的送受端，高相角区域的电网是低相角区域电网的上级电网，低相角区域的电网是高相角区域电网的下级电网。线路断开时，与其相角相近且电气距离最小的线路上的潮流转移量最大［9］。

1.2.1 依据相角范围筛选

设断线线路lef的起点和终点分别是e 和f，其对应的电压相角分别是θ(e)和θ(f)，则lef跨越的相角范围是［θ(f)，θ(e)］，为了保证不漏选潮流转移关键线路，取一个很小的角度ε 作为相角裕度，将lef跨越的相角范围扩展为［θ(f)－ε，θ(e)+ε］。设某并行输电线路lij的起点和终点分别是i和j，其对应的电压相角分别是θ(i)和θ(j)，若lij与lef的相角范围属于图3 的4 种情况之一，则称lij与lef相角相近。

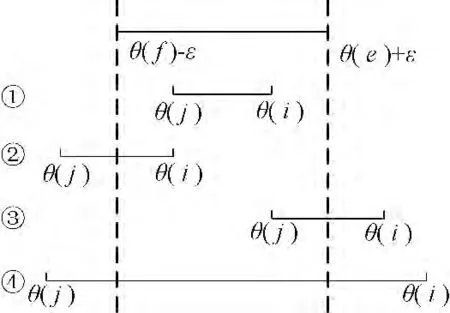
图3 相角范围示意图Fig.3 Schematic diagram of angle range

正常运行时，若节点k，节点i 和节点j 之间的拓扑结构与潮流方向如图4(a)和(b)所示，那么在确定lij的相角范围时，需注意以下两种情况:

(1)节点i 处的负荷为0，如图4(a)所示:lki和lij的功率始终相同，在分析lki或lij的相角范围时，可将节点i 化简消去，直接用lkj代替lki或lij;

(2)节点i 处的负荷不为0，如图4(b)所示:a.若线路lij断开，lki上的功率会减小为负荷功率，lki不属于潮流转移关键线路;b.若线路lki断开，lij上的功率反向，将lij归为易反向线路，直接加入潮流转移关键线路;c.若lki和lij均不断开，由于节点i 处的负荷功率是定值，lki和lij上的功率变化量的大小和方向始终一样，即断线线路断开对lki和lij的潮流影响等同于对lkj的潮流影响，在确定lij的相角范围时，可将节点i 化简消去，直接用lkj代替lij。

需要说明的是，当节点i 处不仅有负荷，同时有发电机注入功率时，如图4(c)所示，若线路lij断开，lki上的功率可能会反向，将lki也归为易反向线路，直接加入潮流转移关键线路。

图4 网络结构示意图Fig.4 Schematic diagram of network structure

1.2.2 依据潮流转移电气距离筛选

由于高压输电网络中线路的电抗值远远大于电阻值，因此，在对线路进行筛选时，可以用电抗值代替阻抗值。

设断线线路lef的起点和终点分别是e 和f，对于其同电源线路，潮流转移电气距离定义为同电源线路的起点到节点e 的最小电气距离加上同电源线路的电抗;对于同负荷线路，潮流转移电气距离定义为同负荷线路的终点到节点f 的最小电气距离加上同负荷线路的电抗。

从与断线线路相角相近的同电源线路(或同负荷线路)中，选出潮流转移电气距离最小的线路，即为等相角并行线路。

需要特殊说明的是，当“发电机—母线”线路属于并行输电线路时，因为短时间内发电机的出力变化很小，不对其进行比较筛选。

1.3 潮流转移关键线路

由等相角并行线路向外扩张范围，根据潮流走向，在相关线路集合中寻找其上游或下游线路。对于某条等相角并行线路，如果它是断线线路的同电源线路，那么该线路与其下游线路属于潮流转移关键线路;如果它是断线线路的同负荷线路，那么该线路与其上游线路属于潮流转移关键线路。

图5 展示了电网中线路集合的从属关系，图中灰色部分代表潮流转移关键线路，集合M 代表等相角并行线路中同电源线路的下游线路，集合N 代表等相角并行线路中同负荷线路的上游线路。

图5 线路集合的关系Fig.5 Relationship of line sets

2 图论及其相关概念

当电网的网络拓扑结构已知时，电力系统可以抽象成一个图，用来反应节点与线路的关系。在搜索断线线路的并行输电线路及相关线路时，需要考虑有功潮流的分布状态，将电网抽象为有向图G0(V0，E0)，其中，V0表示节点集合，E0表示线路集合，E0的方向为线路有功功率的方向;在计算潮流转移电气距离时，需要考虑线路电抗，不需要考虑潮流分布状态，将电网抽象为加权图G1(V1，E1)，其中，V1表示节点集合，E1表示线路集合，E1没有方向，其权值为相应线路的电抗值。

用有向邻接矩阵A 描述G0(V0，E0)，由A获取有向图的路径矩阵P，通过对P 的简单运算，可获得断线线路的并行输电线路及相关线路集合，同时可以方便地得到等相角并行线路的上游或下游线路。用加权邻接矩阵B 描述G1(V1，E1)，利用Floyd 算法可以算出加权图中任意两个节点之间的最短距离。利用邻接矩阵A 求取路径矩阵P［10］和利用Floyd 算法计算两个节点之间的最短距离［11］都已有通用算法，本文不再赘述。

2.1 有向邻接矩阵A

设图中有n 个节点，则A 是一个n ×n 阶的方阵，当vi与vj之间存在1 条由vi直接指向vj的有向边时，则aij=1，否则aij=0。

有向邻接矩阵A 可表示为

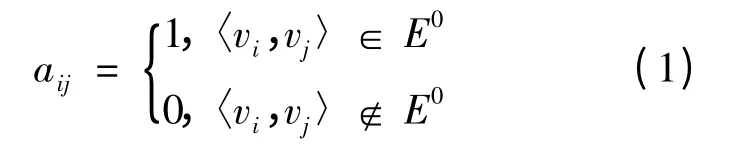
2.2 路径矩阵P

从起点vi出发，若能经过若干线路和节点(不能重复出现)到达终点vj，则称从vi到vj存在路径。路径矩阵P 为

2.3 矩阵运算搜索并行输电线路［12］

设断线线路为lef，其起点和终点分别是e 和f，利用路径矩阵P 求取同电源线路和同负荷线路时，需要引入判别矩阵R 和T，具体过程如下:

(1)令矩阵Q =P +E，其中P 为路径矩阵，E为n×n 的单位矩阵;

(2)取Q 的第f 行行向量Hf，第e 列列向量Le;

若判别矩阵R 中非零元素的行号和列号分别是i 和j，则线路lij是断线线路的同电源线路;同理，若判别矩阵T 中非零元素的行号和列号分别是i 和j，则线路lij是断线线路的同负荷线路。

2.4 加权邻接矩阵B

设图中有n 个节点，则B 是一个n ×n 阶的方阵，当vi与vj之间存在线路时，bij取该线路的电抗值。加权邻接矩阵B 可表示为;式中

式中:Xij为线路lij的电抗值。

3 算法流程

针对情况1 和情况2，利用本文算法搜索潮流转移关键线路的流程图分别如图6 和图7所示。

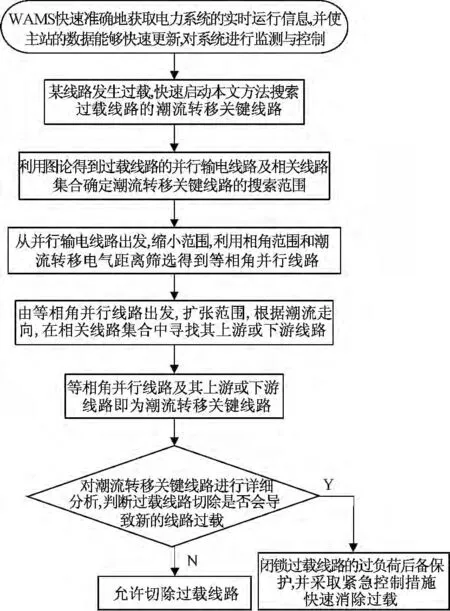
图6 情况1 的算法流程图Fig.6 Flow chart of the algorithm in situation 1

图7 情况2 的算法流程图Fig.7 Flow chart of the algorithm in situation 2

4 仿真验证

为验证本文方法的有效性，对IEEE39 节点系统进行分析计算。

该系统共有39 个节点，46 条线路。当其中的线路30－2，37－25，38－29，31－6，32－10，19－16，20－19，34－20，33－19，35－22，36－23 断开时，电网会变为两个孤立的网络。本文不考虑以上线路断开的情况，针对某种典型运行方式下的潮流分布，依次对全网其他线路进行N－1 分析，并确定相应的潮流转移关键线路。运用PSASP 仿真软件计算线路断开后其他线路的潮流增量，识别实际受线路断开影响严重的线路。

因篇幅有限，本文只列出了该种运行方式下，部分潮流较大的线路断开时对潮流转移关键线路的搜索结果和仿真结果，如表1 和表2所示。(a.不属于断线线路相关线路集合中的线路受线路断开影响很小，表中未将其列出;b.计算并行输电线路的相角范围时，表1 中的线路9－8 要扩展为线路39－8，表2 中的线路22－21 和21－16 要扩展为线路22－16，取相角裕度ε=0.2°)。

仿真结果分析:

(1)准确率:观察表中结果可知，本文方法搜索到的潮流转移关键线路与PSASP 仿真计算的结果基本一致，该方法不仅能准确寻找到潮流方向不变时增量很大的线路，还能寻找到潮流反向后增量很大的线路。本文方法不涉及电网分区，因此不会存在区内支路漏选的情况。

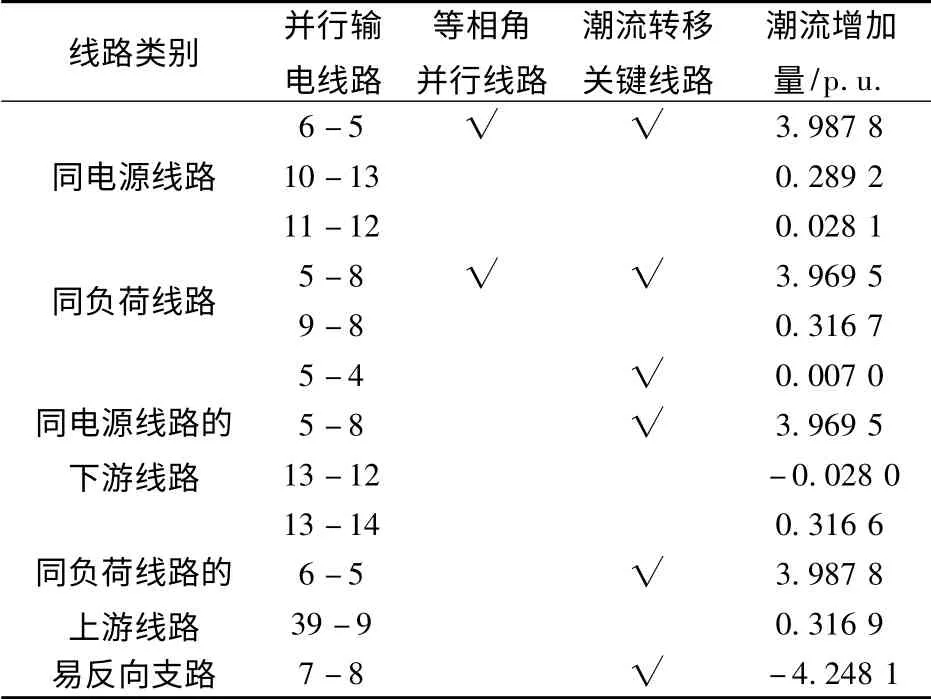
表1 断开线路6-7 时的搜索结果和仿真结果Tab.1 Search results and the simulation results with line 6－7 cut off

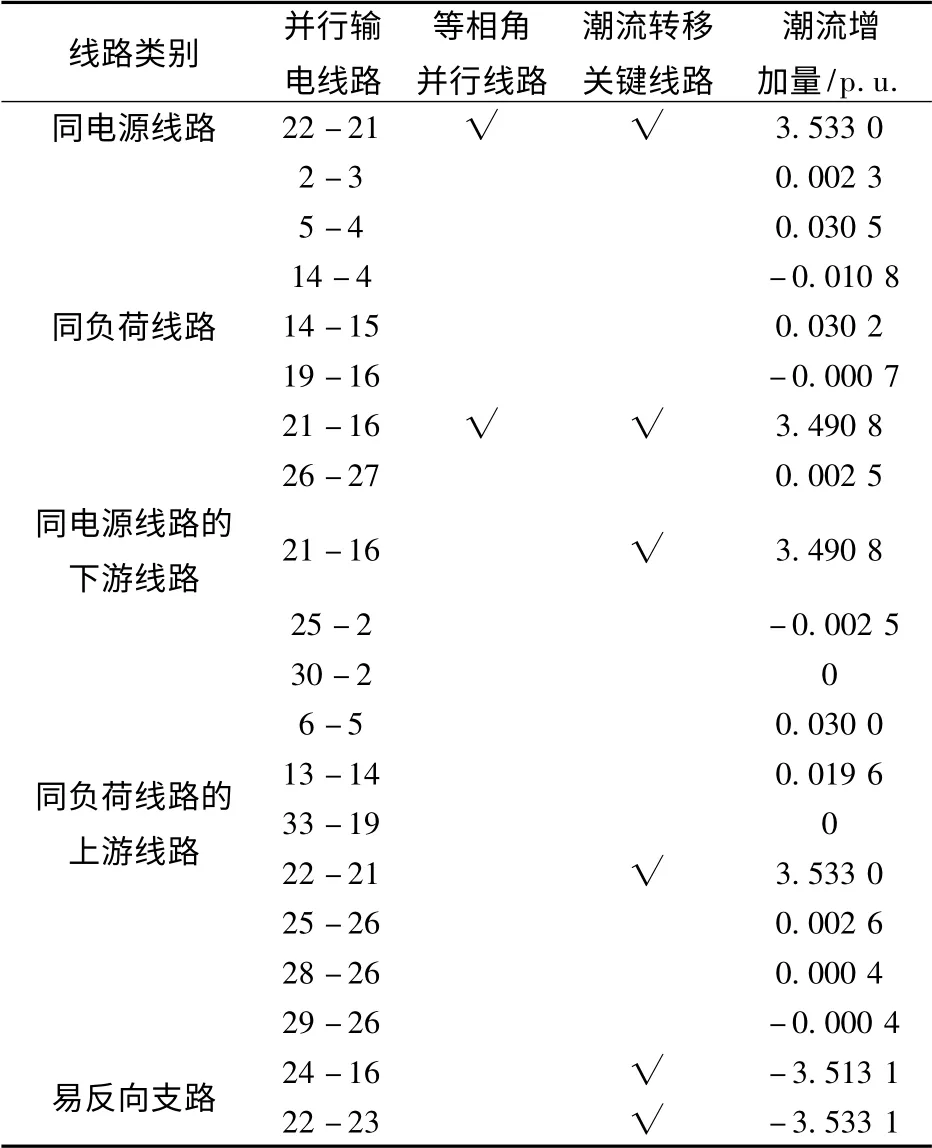
表2 断开23-24 时的搜索结果和仿真结果Tab.2 Search results and the simulation results with line23－24 cut off

(2)运算量:本文方法所涉及的矩阵为稀疏矩阵，可以采用稀疏技术对其进行存储，降低内存占用量，提高计算速度;并行输电线路及相关线路通过简单的矩阵运算就可以得到;并行输电线路数目很少，利用相角范围和潮流转移电气距离筛选得到等相角并行线路时，计算量很少，速度快。文中方法简单，运算量少，不需计算线路功率组成或潮流转移因子等参数。

(3)电网适应性:相关线路集合的大小与电网规模基本无关，不会因为电网规模的扩大而导致计算量大幅度增加的情况，文中方法适合于任意规模的电网。

文中方法运算简单，搜索速度快，在准确率、运算量和电网适应性上有显著优势，且运算时间很短，可以为在线安全分析与控制节约宝贵时间。

5 结论

本文提出了一种基于WAMS 的快速搜索潮流转移关键线路的方法。该方法利用图论确定搜索范围，根据电压相角和线路电抗筛选关键线路。所用方法简单准确，运算量少，搜索速度快，在准确率、计算量以及电网适应性上有显著优势。通过IEEE39 节点系统进行仿真计算，验证了文中算法的有效性和优越性。

［1］李莎，任建文.基于有功增加因子的潮流转移快速搜索［J］.电网技术，2012，36 (12):176－181.

［2］王成山，许晓菲，余贻鑫，等.基于割集功率空间上的静态电压稳定域局部可视化方法［J］.中国电机工程学报，2004，24 (9):13－18.

［3］周德才，张保会，姚峰.基于图论的输电断面快速搜索［J］.中国电机工程学报，2006，26 (12):32－38.

［4］程临燕，张保会，郝治国，等.基于线路功率组成的关键输电断面快速搜索［J］.中国电机工程学报，2010，30 (10):50－56.

［5］倪宏坤，徐玉琴.基于动态规划原理分支界限算法的关键输电断面搜索方法［J］.华北电力大学学报，2009，36 (4):11－15.

［6］张玮，潘贞存，赵建国.新的防止大停电事故的后备保护减载控制策略［J］.电力系统自动化，2007，31 (8):27－31.

［7］Yang Q X，Bi T S，Wu J T.WAMS implementation in China and the challenges for bulk power system protection［C］//Proceedings of Power Engineering Society General Meeting，Tampa，FL，USA:IEEE Power＆ Energy Society，2007:1－6.

［8］徐慧明，毕天妹，黄少锋，等.基于广域同步测量系统的预防连锁跳闸控制策略［J］.中国电机工程学报，2007，27 (19):32－38.

［9］王康，唐陇军，秦康平.利用等相角线的电网潮流转移分析与潮流控制［J］.电力系统自动化，2013，37 (14):117－122.

［10］Berztiss A T.Data structures:theory and practice，second edition［M］.New York:Academic Press，1975.

［11］卢开澄，卢华明.图论及其应用［M］.北京:清华大学出版社，1995.

［12］王英英，罗毅，涂光瑜，等.采用图论的电网连锁故障模式搜索方法［J］.高电压技术，2010，36(2):401－405.