EEMD-HHT方法在双馈式感应发电机定子匝间短路故障分析中的应用研究

李俊卿，于海波，张立鹏

(华北电力大学电气与电子工程学院，河北保定071003)

0 引言

在全球经济急剧增长的今天，人类对能源的需求越来越大，风能作为一种重要的可再生能源，因其清洁、无污染等优点而备受关注。

目前，已投入运营的风力发电机组以双馈感应发电机为主。定子匝间短路故障作为一种常见的电气故障，约占电机故障的30 %以上，因此双馈感应发电机故障的监测与早期诊断，对维护电机和电网的安全稳定运行，有着重要的意义。

针对双馈式风力发电机的故障诊断研究也是逐渐开始涌现，目前，不少国内外的学者加入其中，并取得了一定的成果。文献［1］提出利用短路故障时的负序电流作为特征量，对电机进行故障诊断;文献［2］根据匝间短路故障程度与定子阻抗参数之间的关系，基于有限元方法进行故障诊断;文献［3］提出通过测转子电流谐波和搜索线圈电压的方法来分析定子匝间故障;文献［4］提出了基于GA 与BP 相结合的以及遗传规划法诊断方法;文献［5］使用有限元和离散小波变换对异步电动机内部故障进行建模和诊断分析。

本文利用多回路理论的方法建立双馈式发电机的数学模型，通过MATLAB 仿真模拟出电机定子绕组匝间短路故障以及其他情况，采用希尔伯特－ 黄变换(Hilbert-Huang Transform，HHT)和EEMD-HHT 方法分别对目标电流进行故障的分析处理，比较两方法的优劣。

1 HHT 方法和EEMD-HHT 方法

HHT 方法由台湾中央研究院院士黄锷等人提出［6］，该方法分为两个部分:首先将目标信号分解为本质模态函数(IMF)，这样的分解流程称为经验模态分解(EMD);然后对IMF 作希尔伯特(Hilbert)变换，从而正确地获得信号时频平面下的能量分布频谱图。

1.1 EMD 方法分解原理

任何一个信号，只有满足下面两个条件［6］，才能进行EMD 分解:

(1)局部极大值以及局部极小值的数目之和必须与零交越点的数目相等或是最多只能差1;

(2)在任何时间点，局部最大值所定义的上包络线与局部极小值所定义的下包络线，取平均要接近零。

分解方法的具体步骤如下:

步骤1:找出信号x(t)中的所有局部极大值和局部极小值，接着利用三次样条，分别将局部极大值串连成上包络线与局部极小值串连成下包络线;

步骤2:求出上下包络线之平均，得到均值包络线m1(t);

步骤3:原始信号x(t)与均值包络线相减，得到第一个分量h1(t)，如式(1)所示:

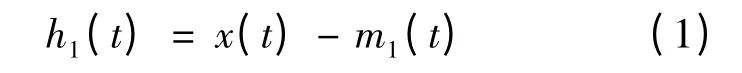
步骤4:如此重复，直到hk(t)符合IMF 的条件，即得到第一个IMF 分量c1(t)，如式(2)所示:

步骤5:原始信号x(t)减去c1(t)可得到剩余量r1(t)，表示如式(3):

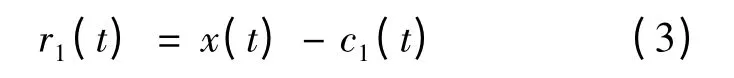
步骤6:将r1(t)当作新的资料，重新执行步骤1 至步骤5，得到新的剩余量。如此重复n 次直至达到目标要求。

这样，原始信号x(t)可以表示成n 个IMF 分量与一个平均趋势分量rn(t)的组合，表示如式(4):

1.2 EMD 方法的不足

EMD 方法是一种自适应的、高效的信号分解方法，适合于处理非线性、非平稳信号［7］。它通过“筛选”从目标信号中提取出IMF。

但是，EMD 方法也存在自身的不足。当数据不是纯的白噪声时，一些尺度会丢失，这样就会出现模态混叠现象［8］。所谓模态混叠，即一个IMF分量包括了尺度差异较大的信号，或是一个相似尺度的信号出现在不同的IMF 分量中。模态混叠的原因是信号的间断，这种间断不仅在时频分布中引起了严重的混叠，而且使单独的IMF 分量缺乏物理意义［9］。现实中的所有数据都融合了信号和噪声，因此EMD 的模态混叠现象是不可避免的。

1.3 EEMD 方法原理

EEMD(集合经验模态分解)方法，是针对EMD 方法的不足，提出的一种噪声辅助数据分析方法。

EEMD 分解原理为当给信号附加的白噪声均匀分布在整个时频空间时，该时频空间就由滤波器组分割成的不同尺度的成分组成。当目标信号加上均匀分布的白噪声背景时，不同尺度的信号区域将自动映射到与背景白噪声相关的适当尺度上去。每个独立的测试都可能会产生非常嘈杂的结果，这是因为每个附加噪声的成分都包括了信号和附加的白噪声。因为在每个独立的测试中噪声是不同的，所以当使用足够测试的全体均值时，噪声将会被消除。全体的均值最后将会被认为是真正的结果，唯一持久稳固的部分是信号本身，所加入的多次测试是为了消除附加的噪声［10］。

这种改进型的EMD 分解方法分解步骤为:

步骤1:通过给目标信号加一组白噪声来获得一个新的信号;

步骤2:对该新的信号进行EMD 分解，得到各IMF 分量;

步骤3:给目标信号加入不同的白噪，重复以上两步;

步骤4:分解后得到各自的IMF 分量组;

步骤5:取相应IMF 均值作为最终的IMF 组;

步骤6:取相应的剩余分量的均值作为最终的IMF 组。

1.4 希尔伯特变换

通过分解得到IMF 后，就可以对每一个分量做希尔伯特变换，得到其瞬时频率和幅度。对任意时间序列x(t)，希尔伯特变换Y(t)定义为

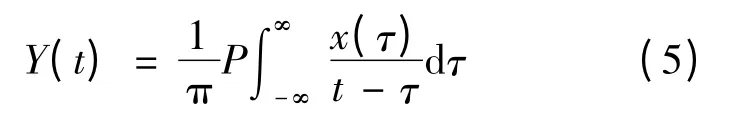
式中:P 表示柯西主值。

根据这一定义，当x(t)与Y(t)形成一个复共轭时，就可得到一个解析信号Z(t):

2 多回路的数学模型

［11］给出了正常情况下的多回路数学模型，公式如式(7):

式中:U 为由定子支路电压、转子回路电压以及励磁绕组电压构成的电压列矩阵;I 为由定子支路电流、转子回路电流以及励磁绕组电流构成的电流列矩阵;p 为微分算子;R 为由定子支路电阻、转子回路电阻以及励磁绕组电阻构成的电阻矩阵。

另外，磁链ψ 又为

式中:L 为由定、转子绕组间的自感及互感构成的矩阵。带入式(7)中，得出:

根据回路可知，正常情况下，支路与回路间的转换矩阵H 可表示为

将H 矩阵带入式(9)中，即(9)式两侧同时乘以H，整理后得出:

定、转子支路和回路电流满足式:

式中:I′ 为定、转子回路电流。

将式(12)带入(11)整理后，得:

经过替代，式(13)可简化为

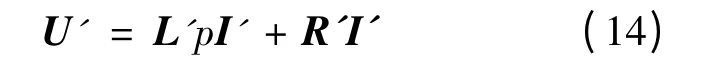
式中:U′ = HU，L′ = HLHT，R′ = pL′ + HRHT。

以回路电流为目标变量，对式(8)进行整理:

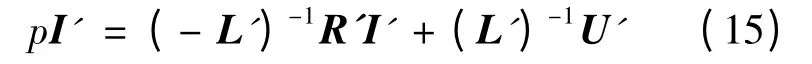
式中:U′ 为回路电压列向量。

经过上述变换，一个电机的多回路数学模型就建好了。通过MATLAB 编程模拟故障，利用4阶龙格库塔法，对式(15)进行求解，可得电机的定、转子各回路电流，再由式(12)转换，得定、转子各支路电流。当定子发生匝间短路故障时，短路匝形成一个新的回路。这样，在分析计算中加入这个新的回路，采用同样的方法，就可求得不同程度故障时的各物理量。

用多回路理论建立电机的数学模型，充分考虑了电机绕组间的自感、互感、气隙互感以及漏电感等因素，使得计算结果更准确。

3 仿真结果分析

本文以上述理论为基础，对一台5.5 kW 双馈式异步风力发电机进行了仿真。电机的基本参数如下:额定功率5.5 kW;额定频率50 Hz;额定电压380 V;定子槽数36;转子槽数24;极对数2;定子并联支路2;转子并联支路1;定子每线圈匝数37;转子每线圈匝数12;定子每支路电阻值2.498 Ω;转子每条支路电阻值0.478 Ω。电机在定子电压380 V 下运行，转子励磁电压36.5 V，转子转速1 200 RPM。

分别对电机正常运行、定子匝间短路和电压不平衡等不同故障情况、不同故障程度进行了仿真。模拟匝间短路故障时，电机定子C 相某一线圈发生匝间短路;模拟电压不平衡故障时，电机定子三相电压不对称，A 相电压下降。定义定子B，C 相合成的线电流为Ib，A，C 相合成的线电流为Ic，A，B 相合成的线电流为Ia。

电机正常运行及不同故障情况下的定、转子三相线电流波形如图1～图3所示。

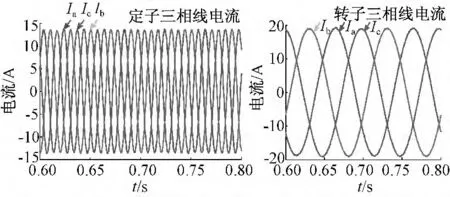
图1 正常情况下定、转子三相线电流Fig.1 Normal three-phase line current of stator and rotor

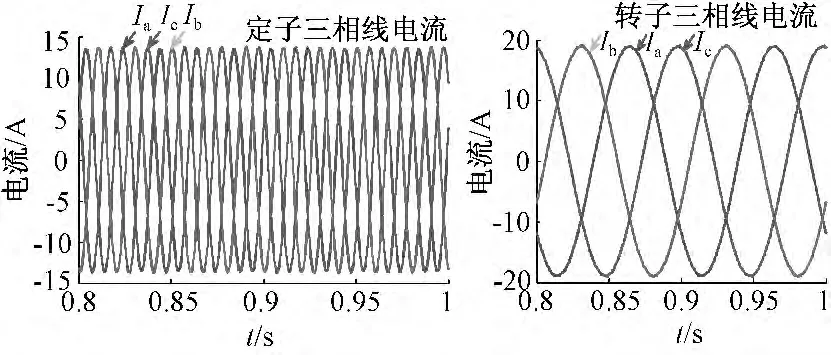
图2 定子C 相2 匝短路后的定、转子三相线电流Fig.2 Three-phase line current of stator and rotor after stator C-phase occurring 2－turn short circuit

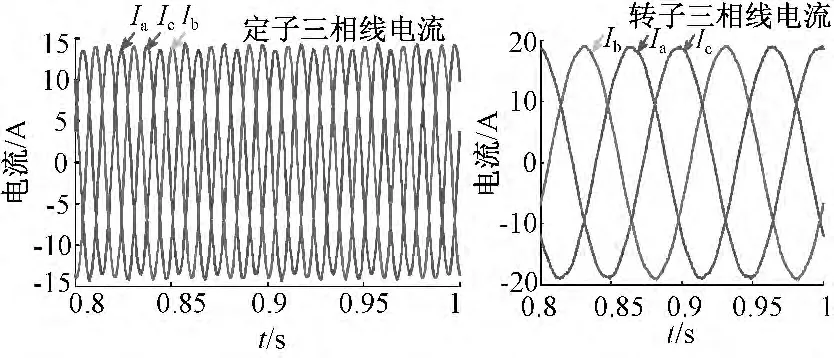
图3 定子C 相5 匝短路后的定、转子三相线电流Fig.3 Three-phase line current of stator and rotor after stator C-phase occurring 5－turn short circuit

如图1～图3所示，双馈式电机正常运行时，定子侧三相电流大小相等，相位相差120°，转子侧波形平滑;当发生2 匝、5 匝短路时，三相定子电流不再对称，电流Ib，Ic幅值均有不同程度的增大，故障程度越深，增幅越大;转子三相线电流波形由于谐波影响，均有不同程度的波动，故障程度越深，波动越明显，但三相电流基本保持对称。该仿真结果符合电机设计原理。

3.1 定子匝间短路故障的分析结果比较

对上述多回路数学模型仿真出来的结果，进行HHT 和EEMD-HHT 处理，由仿真过程可知，电机从0 s 开始运行，直至0.6 s 左右达到稳态，在0.8 s 处发生定子匝间2 匝短路。定子电流Ic的分析结果如图4～图6所示。

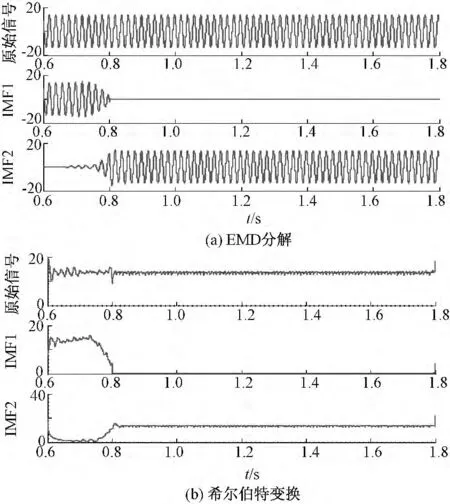
图4 定子2 匝短路后电流Ic 的HHT 分析结果Fig.4 HHT result of Ic after stator occurring 2－turn short circuit

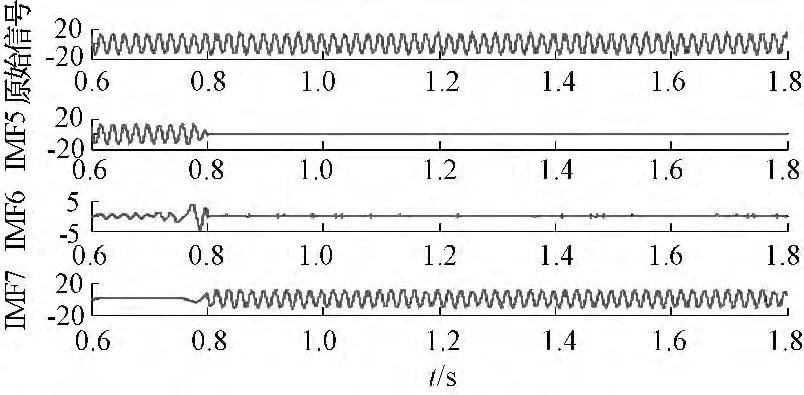
图5 定子2 匝短路后电流Ic 的EEMD 分解Fig.5 EEMD decomposition of Ic after stator occurring 2－turn short circuit

如图4～图6所示为电机在稳定后的0.6 s 时刻开始，到0.8 s 发生匝间短路故障后，电流Ic的HHT 和EEMD-HHT 变换。EEMD 分解的各层IMF 中，IMF 的5～7 层曲线能反映电流故障情况，而前几层并不包含效信息，因此，为了让结果更加直观明显，EEMD-HHT 变换后的1～4 层IMF 图形没有给出。

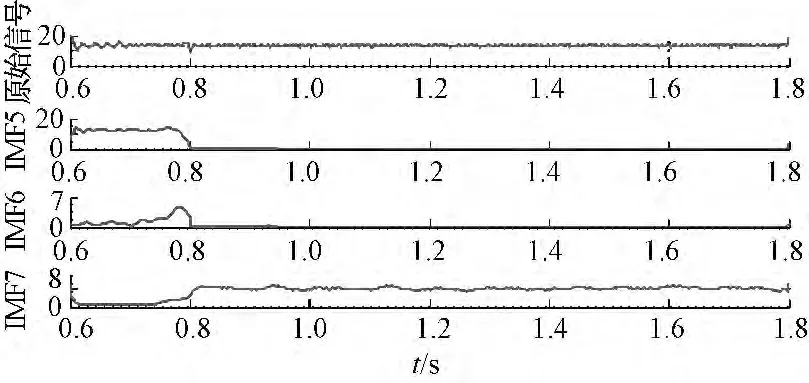
图6 定子2 匝短路后电流Ic 各IMF 的希尔伯特变换Fig.6 Fig.6 Hilbert transform of each IMF of Ic after stator occurring 2－turn short circuit

图4(a)中IMF 的1～2 层，可见在0.8 s 处波形发生了明显变化，可以理解为EMD 方法将一个整体信号在0.8 s 处分成了两部分，这是因为在故障发生后，电流的幅值、相位等都发生了变化，从而引起信号包络线的改变，使信号包络线含有故障信息，被EMD 所识别;图4(b)中的波形，是对图5(a)中各层IMF 作希尔伯特变换所得，图中IMF 的1～2 层波形幅值在0.8 s 处发生阶跃性突变，是根据IMF 结果作希尔伯特变换所得到的高频分量，这更加直观明确地反映了该时刻的异常。由仿真过程可知该时间点为故障发生点，那么HHT 方法能够反映故障的发生，准确地确定时间点，利于进一步判断电机的故障情况。同样，对故障后的电流Ic作EEMD-HHT 变换，图5、图6 中IMF 的5～7 层也产生了该现象，这说明这两种方法运用在电机定子匝间短路故障诊断分析中是可行的。

上文是从0.6 s 开始的分析，如果从电机刚启动开始，或电机稍有不稳定情况时开始分析，那么传统的EMD 方法存在的问题就会凸显。另外，希尔伯特变换的结果虽然从能量角度说明了分析结果，但其效果和结论与EMD 或EEMD 分解结果相类似，因此，下面不再给出该变换的分析情况。已知电机从0 时刻开始启动，在0.8 s 处发生定子2匝短路故障，电流Ic的分析结果如图7～图8所示。

已知电机开始运行时刻为0 s，到0.6 s 左右达到稳态，在0.8 s 处发生定子2 匝短路故障，图7和图8 反映了电机从启动开始，在0.8 s 处发生了匝间短路故障的情况。如图7所示，对于传统的EMD 分解，其故障点处的波形存在干扰情况，这是因为电机在启动后，从非稳定状态进入稳定状态，而后又进入故障状态，在这3 个状态中，传统的EMD 分解方法不能有效地区别非稳定状态和故障状态，这就造成了将电流信号分成3 部分的情况，同时也无法准确定位故障时间点，这势必会对电机故障的判断产生一定的干扰。

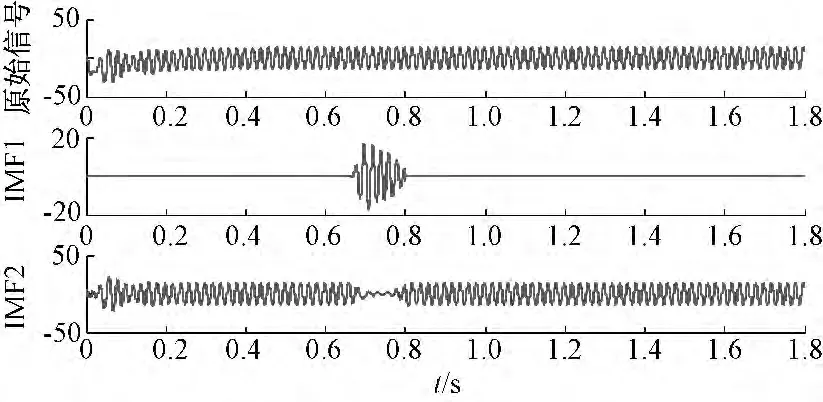
图7 0 s 开始的2 匝短路后电流Ic 的EMD 分解Fig.7 HHT of 2－turn short circuit Ic from 0 s

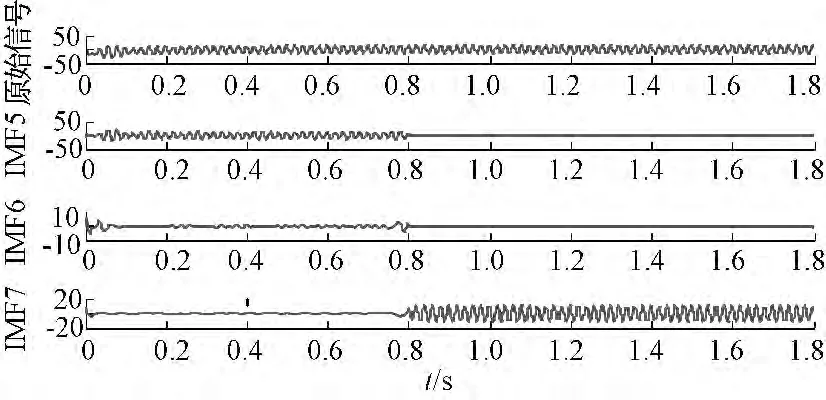
图8 0 s 开始的2 匝短路后电流Ic 的EEMD 分解Fig.8 Fig.8 EEMD decomposition of 2－turn short circuit Ic from 0 s

但是用EEMD 方法替换了EMD 方法后，分解出来的结果则很好地排除了这一干扰，如图8 中IMF 的5～7 层所示，电流的波形只是在0.8 s 处被分成了两段不同的波形。这是因为不稳定状态下的电流的变化，并不是EEMD 所默认的“筛选”情况。EEMD 方法能够正确地将电机的状态归类成两种，即非故障状态和故障状态，没有将稳态和非稳态与故障状态相混淆。

综上可知，当电机发生短路故障时，定、转子电流的幅值变化并不明显，很难直观地通过电流变化判断出电机的异常，经过HHT 或EEMD-HHT方法处理后，能清晰地判别出电机发生故障的时刻，继而可提取故障处的电流做下一步的故障诊断。以上分析说明，HHT 或EEMD-HHT 方法可以用来进行双馈电机定子匝间短路故障的诊断。

但是HHT 方法中的EMD 分解存在不足，导致电机运行时有不稳定状态就会被该方法识别出来，从而影响对故障发生的判断。EEMD 方法则很好地弥补了这一不足，采用噪声的多次加入和消除，将电流不稳定的情况排除，只保留了对定子匝间短路故障电流的识别特性，从而达到分离目标信号故障状态和非故障状态的目的。

3.2 变转子转速情况的分析结果比较

由于双馈式风力发电机的转子转速随风速的变化而变化，所以当考虑风速变化的影响时，对分析结果进行对比。已知仿真过程，电机启动并稳定后，在0.8 s 处转子转速由1 200 RPM 变成1 350 RPM。

上一小节指出，电机启动后的前期不稳定状态会被EMD 分解方法误检出来，那么下面的仿真分析中，如果从电机启动的0 s 时刻开始分析，都会存在同样的问题，为了不再赘述，以下仿真分析都从电机进入稳态后的0.6 s 开始。如图9～图10所示。

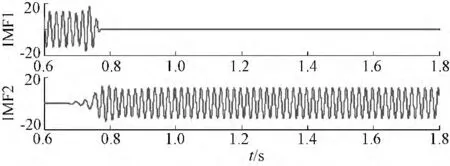
图9 变风速后电流Ic 的EMD 分解Fig.1 Fig.9 EMD decomposition of Ic of wind speed change

图10 变风速后电流Ic 的EEMD 分解Fig.10 EEMD decomposition of Ic of wind speed change

如图9 中IMF 的1～2 层IMF所示，传统的EMD 分解对0.8 s 处的转速变化情况做出了反应，在0.8 s 左右将波形分成了两部分，电流的变化被误检出来。而如图10所示，EEMD 分解出来的结果则并无明显的信号被分类情况，这是因为风速变化导致转子转速变化，但是该变化所引起的电流幅值和谐波的改变并不是EEMD 所默认的情况，其变化后的包络线不会被该方法所分类，因此不会将其作状态区分。整个过程中，0.8 s 处转子转速的变化的EEMD 分解结果与定子匝间短路故障的结果明显不同，这说明EEMD-HHT 变换能更好地反映出电机故障的发生，减少了风速变化因素对匝间短路故障判断的影响。

在新能源实验室，利用双馈风机模型对变风速情况进行了实验模拟，实验时，风速由1 260 RPM 变到1 370 RPM。将所得定子电流Ic进行EMD 和EEMD 分解分析后，与仿真结果所得现象相符合，由于实验过程中含有噪声，因此EMD 分解时IMF 的3～4 层出现预期结果，已知风速变化时刻在0 到0.1 s 之间，实验分析结果如图11～图12所示。

图11 变风速实验电流Ic 的EMD 分解Fig.11 EMD decomposition of Ic of wind speed change experiment

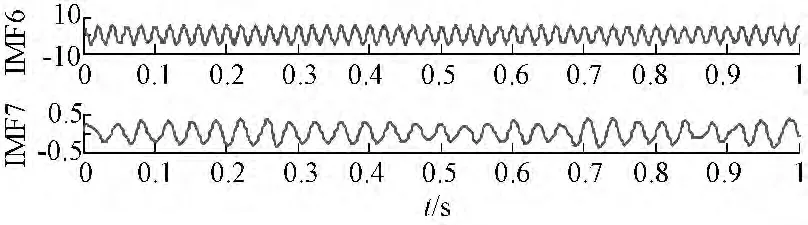
图12 变风速实验电流Ic 的EEMD 分解Fig.12 EEMD decomposition of Ic of wind speed change experiment

3.3 电压不平衡时分析结果比较

定子电压不平衡的情况下，也会造成三相电流的不平衡，并产生谐波，而且谐波含量与定子匝间短路故障时电流的谐波含量相类似。如果从电流方面来分析判断匝间短路故障，那么不平衡故障则是定子匝间短路故障诊断中最大的干扰因素。

利用上述多回路模型对定子电压不对称故障进行仿真，电机从0 s 处启动，0.6 s 达到稳定，不对称故障依然发生在0.8 s 处，故障时定子A 相电压下降20 %，从电机0.6 s 稳态后开始分析，定子故障电流Ic的分析结果如图13～图14所示。

图13 A 相电压下降20 %后电流Ic 的EMD 分解Fig.13 EMD decomposition of Ic after A-phase voltage dropping 20 %

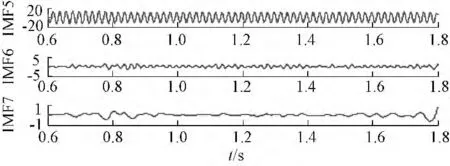
图14 A 相电压下降20 %后电流Ic 的EEMD 分解Fig.14 EEMD decomposition of Ic after A-phase voltage dropping 20 %

由图13 中可以看到，由于负载不平衡的加入，电流发生了变化，导致HHT 方法中的EMD 分解结果在0.8 s 故障发生处产生了明显的短暂的振动，这样容易造成对故障的误判，给诊断过程以干扰。如图14所示，EEMD 分解的过程中，分析出来的包络线等量没有将电流的变化信息作为故障量提取出来，对电流所包含信息进行了自动“识别”，分解结果在0.8 s 发生不平衡故障的时间点处，并没有明显的振荡情况。该方法并没有将电压不平衡情况作为电机故障检测出来，虽然波形幅值或趋势有微弱的变化，但这与匝间短路故障的现象有很大不同，二者容易辨认。该方法有效地区分了两种故障情况，避免了不对称故障在定子匝间短路故障诊断过程中的干扰。

在新能源实验室，通过双馈式风力发电机进行定子电压不平衡情况的实验模拟，实验时B 相电压不平衡，故障发生在0.2 s 左右，所得定子电流Ic经EMD 和EEMD 分解后，与仿真结果所得现象相符合，不再进行分析，实验结果如图15～图16所示。

在新能源实验室利用双馈式风力发电机模型进行了负载不平衡情况和变风速情况的实验模拟，经过分析得出EMD 和EEMD 方法的分析结果与仿真分析结果相符合，由此也进一步说明了结论的真实性和可靠性。

图15 电压不平衡实验电流Ic 的EMD 分解Fig.15 EMD decomposition of Ic of voltage unbalance experiment

图16 电压不平衡实验电流Ic 的EEMD 分解Fig.16 EEMD decomposition of Ic of voltage unbalance experiment

4 结论

运用多回路理论对双馈式风力发电机建模，采用MATLAB 进行不同情况或故障的仿真，并通过实验验证仿真分析结果。通过对不同情况下电流的分析可知，由于HHT 方法中的EMD 分解存在的缺陷，导致了该方法在电机不稳定、转子转速变化、定子电压不平衡等多种情况下，分解出来的结果存在问题，出现与匝间短路故障相类似的现象，容易造成对定子匝间短路故障的误判。而采用EEMD 分解替换传统的EMD 分解，则有效地弥补了这一不足。经过与EMD 的对比可知，电流经EEMD 分解后，当定子发生匝间短路故障时，分解结果的波形才会在故障点出被分段识别，希尔伯特变换后的幅值产生明显的突变，而其他情况的分析结果并无此现象。EEMD-HHT 方法不仅能准确找出故障的时间点，而且有效地滤除了其他因素对定子匝间短路故障诊断的干扰，能够为双馈电机定子匝间短路故障的诊断提供更加可靠的帮助。

参考文献:

［1］马宏忠，张志艳，张志新，等.双馈异步发电机定子匝间短路故障诊断研究［J］.电机与控制学报，2011，15 (11):50－54.

［2］张志新，马宏忠，钱雅云，等.基于磁场变化的双馈异步风力发电机定子绕组匝间短路故障仿真分析［J］.电网与清洁能源，2012，28 (9):68－72.

［3］Shah D，Nandi S，Neti P.Stator inter turn fault detection of doubly-fed induction generators using rotor current and search coil voltage signature analysis［J］.IEEE Industry Applications Conference，2007，23(7):1948－1953.

［4］李之昆.发电机转子绕组匝间短路故障诊断的研究［D］.南京:河海大学，2004.

［5］Mohammed O A，Abed N Y，Ganu S.Modeling and characterization of induction motor internal faults using finite-element and discrete wavelet transforms［J］.Magnetics，IEEE Transactions on，2006，42 (10):3434－3436.

［6］N E Huang，Z Shen，S R Long，et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis［C］.Proceedings of the Royal Society of London，1998，454:903－ 995.

［7］李天云，赵妍，李楠，等.基于HHT 的电能质量检测新方法［J］.中国电机工程学报，2005，25(17):52－56.

［8］张璨，文福拴，王建军，等.联合采用高通低通滤波与Hilbert－黄变换的非线性信号分析［J］.华北电力大学学报，2013，40 (2):5－9.

［9］陈可，李野，陈澜.EEMD 分解在电力系统故障信号检测中的应用［J］.计算机仿真，2010 (3):263－266.

［10］张鑫，吴亚锋，朱帅琦.基于EEMD-HHT 边际谱的轴承故障诊断［J］.科学技术与工程，2011 (11):7625－7629.

［11］高景德，王祥珩，李发海.交流电机及其系统的分析(第2 版)［M］.北京:清华大学出版社，2005.