电动汽车充电设施多阶段最优规划

韩伟强，王贵斌，文福拴

(1.国网浙江省电力公司电动汽车服务分公司，浙江杭州310007;2.深圳大学机电与控制工程学院，广东深圳518060;3.文莱科技大学，斯里巴加湾BS8675;4.浙江大学电气工程学院，浙江杭州310027)

0 引言

影响电动汽车(electric vehicle，EV)推广应用的因素很多，EV 充电设施匮乏就是其中一个。这样，如何规划EV 充电设施就是一个需要研究的重要问题。EV 充电设施大体上可以分为换电站、快速充电站和分散式充电桩3 种［1～6］。

在最近几年中，国内外在EV 充电设施规划方面已经做了一些研究工作。文献［2］研究了EV充电站的选址和定容问题，并考虑了交通网络动态模型和时空限制。文献［3］提出了考虑环境因素和服务半径的两步式方法，首先得到EV 充电站的可能候选解，之后采用内点法求解目标函数中含有投资成本、运行成本和网络损耗的充电站多目标规划模型。在文献［4］中，通过采用一个简化的输电系统分区模型和发电容量分区模型，研究了在2009～2025年期间如何充分利用安大略省的电力系统潜在能力来满足EV 负荷的充电需求。文献［5］发展的充电站最优规划模型充分考虑了电力系统和交通系统的约束，并采用鲁棒优化方法求解。文献［6］研究了充电桩的最优布局问题，其中包括了一种智能负荷管理方法，综合考虑了降低高峰负荷、改善电压曲线和降低网络网损等目标。

从总体上讲，到目前为止对EV 充电设施规划的研究仍处于初级阶段。在现有的相关文献［2～6］中，大多数采用了单目标水平年规划。充电设施规划需要考虑多方面的因素，如EV 车主的行驶行为、配电系统和交通系统的拓扑结构、电力系统运行的安全性和经济性等，这些因素会导致EV 和各类充电设施的发展前景具有很强的不确定性。采用时间跨度很长的水平年规划方法对充电设施进行规划并不合适。为了在充电设施规划中合理考虑上述不确定性因素，规划工作按多阶段进行比较合适，因为在不同的时间跨度不确定性因素所覆盖的范围和程度都不相同。

在上述背景下，本文研究EV 充电设施的多阶段、多目标规划问题，并充分考虑了配电系统和交通系统的运行约束和运行目标。为便于描述，本文的研究针对两阶段规划，但所提出的方法思路与实现架构可以容纳一般的多阶段规划问题。

本文提出采用数据包络分析(data envelopment analysis，DEA)对不确定性场景下充电设施规划的成效进行综合评估。DEA 是一种包括多输入和多输出变量的多维评估方法［7］，可用于辅助决策人员比较一组候选解的性能，候选解在DEA中被称为决策单元(decision－ making units，DMUs)［8］;采用DEA 可以选出最优的候选解。DEA 是一种先进的评估方法，具有下述优点:a.可同时评估含有多组输入和输出的复杂系统;b.规划决策者的倾向性可以被合理考虑;c.DEA 和优化问题紧密相关，可以充分利用成熟的优化理论和方法进行求解和分析。

在所提出的充电设施多阶段最优规划方法中，首先针对第1 阶段规划产生1 组可以接受的次优结果。对于下1 阶段发展中存在的不确定性因素，通过对随机因素进行抽样生成第2 阶段的不同场景，再针对不同场景分别进行第2 阶段规划。采用DEA 评估不同场景下第2 阶段规划的效率值，以辅助决策者对采取何种第1 阶段规划方案做出合理决策。所提出的方法框架如图1所示。

图1 包括DEA 评估的EV 充电设施多阶段规划方法Fig.1 Multistage planning framework for EV charging facilities with DEA evaluation included

1 DEA 简介

假设要评估的系统中含有n 组决策单元(DMU)，每个决策单元有m 个输入变量(x)和s个输出变量(y)，那么第k 个决策单元的有效值Ek可以描述为

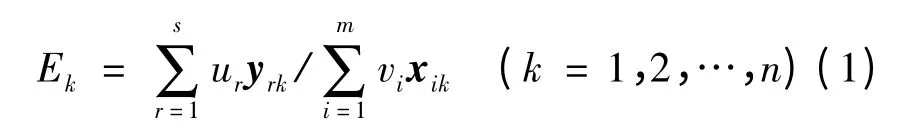
式中:s 为输出变量(y)个数;m 为输入变量(x)个数;xik和yrk分别为第k 个决策单元的第i 个输入和第r 个输出;vi和ur分别为与xik和yrk相关的系数，可以由问题的解得出。

在获得了第k 个决策单元的有效值Ek后，DEA 模型可以描述为

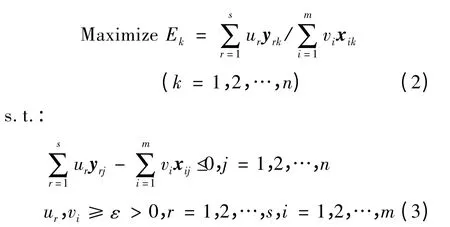
在有些情形下，可能存在多个决策单元的有效值相等且都为1，此时就无法根据有效值将决策单元合理排序。为避免这一问题，可以采用改进的DEA 方法，即超效率DEA 方法:

如果系统对于输入变量和输出变量有其它要求，可以将相关要求或约束整合进式(4)和(5)中。例如，决策者的倾向性信息可以采用对权重进行约束的形式整合到DEA 模型中:

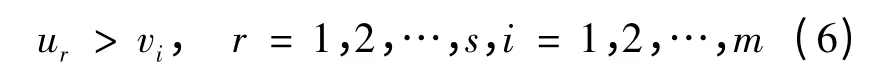
计及决策者倾向的DEA 模型用式(4)～(6)描述。

2 充电设施多目标规划模型

在对EV 充电设施进行规划时，需要兼顾多个方面的目标，满足不同类型的约束。在本节所构造的EV 充电设施规划模型中，考虑了下述3种约束:a.最大化充电服务能力;b.最小化系统网损;c.最小化电压偏移。当然，也可以根据具体规划问题的需要，考虑其它优化目标。

(1)最大化充电服务能力。EV 充电设施规划的主要目标就是最大化充电设施的服务能力，这可用俘获的EV 车流量来衡量，而车流量是由交通系统中EV 的行驶路径决定的。

EV 车主通常会选择从起点到终点的最短路径作为自己的行驶路径。最短路径可以由Dijkstra或Floyd 算法求出［9］。定义EV 车流量为行驶在给定路径上的EV 数量。

最大化充电服务能力目标可以用最大化行驶在道路上的EV 车流量来描述:

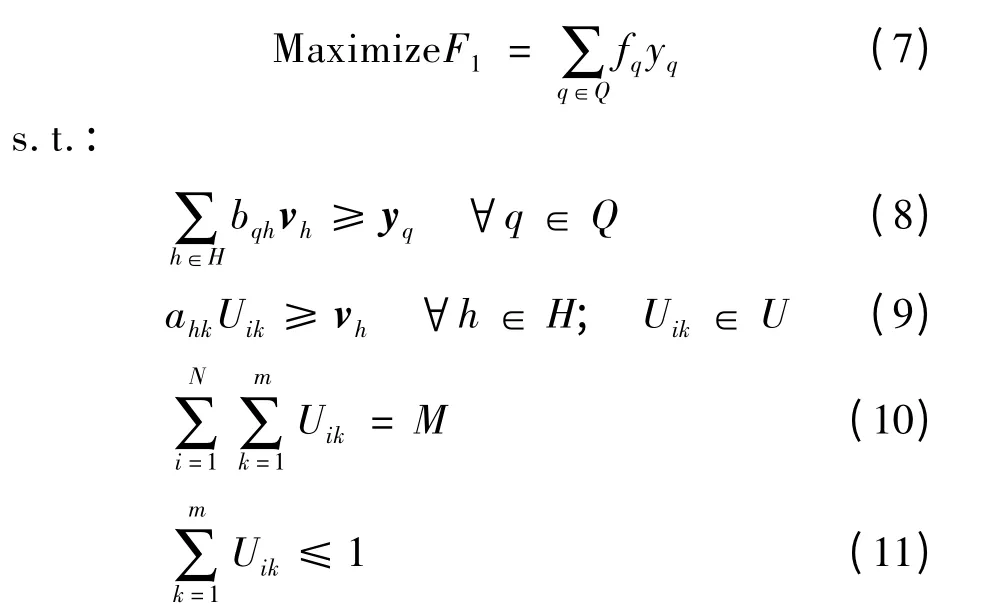
式(7～11)中:q 为起点O 到终点D 的最短路径;Q为所有路径的集合;m 为充电设施类型数量;N 为交通网络节点数;M 为将要建设的EV 充电设施数量;fq为路径q 上的车流量;U 为所有可能的充电设施位置集合;h 为充电设施候选方案的编号;H为所有充电设施规划方案的集合;如果EV 车流量fq可以被充电，yq=1，否则yq=0;如果规划方案h可以满足fq的充电需求，bqh=1，否则bqh=0;如果规划方案h 中的所有充电设施都可以正常运行(未处于检修状态或超出容量限制)，vh=1，否则vh=0;如果充电设施k 在规划方案h 中，ahk=1，否则ahk=0;如果EV 充电设施位于节点i 上，Uik=1，否则Uik=0。

式(8)所表示的约束要求至少有一个充电设施规划方案h 可以满足路径q 上的充电需求，合理的充电设施规划方案应该在EV 行驶路径上规划1 个或多个充电设施;式(9)表明只有当规划方案h 中的所有充电设施都不违反运行约束(如被检修或超出容量限制等)时，vh为1;式(10)要求在规划方案中共有M 座充电设施需要被建设;式(11)表明一个节点上一次只能建设一种充电设施。

(2)最小化系统网损和电压偏移。当新建的EV 充电设施接入配电系统后，系统中的潮流分布会发生变化，也就会导致配电系统的网络损耗发生变化。因此，充电设施规划中要合理考虑降低配电系统网损。EV 充电也会导致节点电压偏移发生变化，影响配电系统安全稳定运行。这里将降低系统网损和减少电压偏移作为EV 充电设施规划的另外两个优化目标:

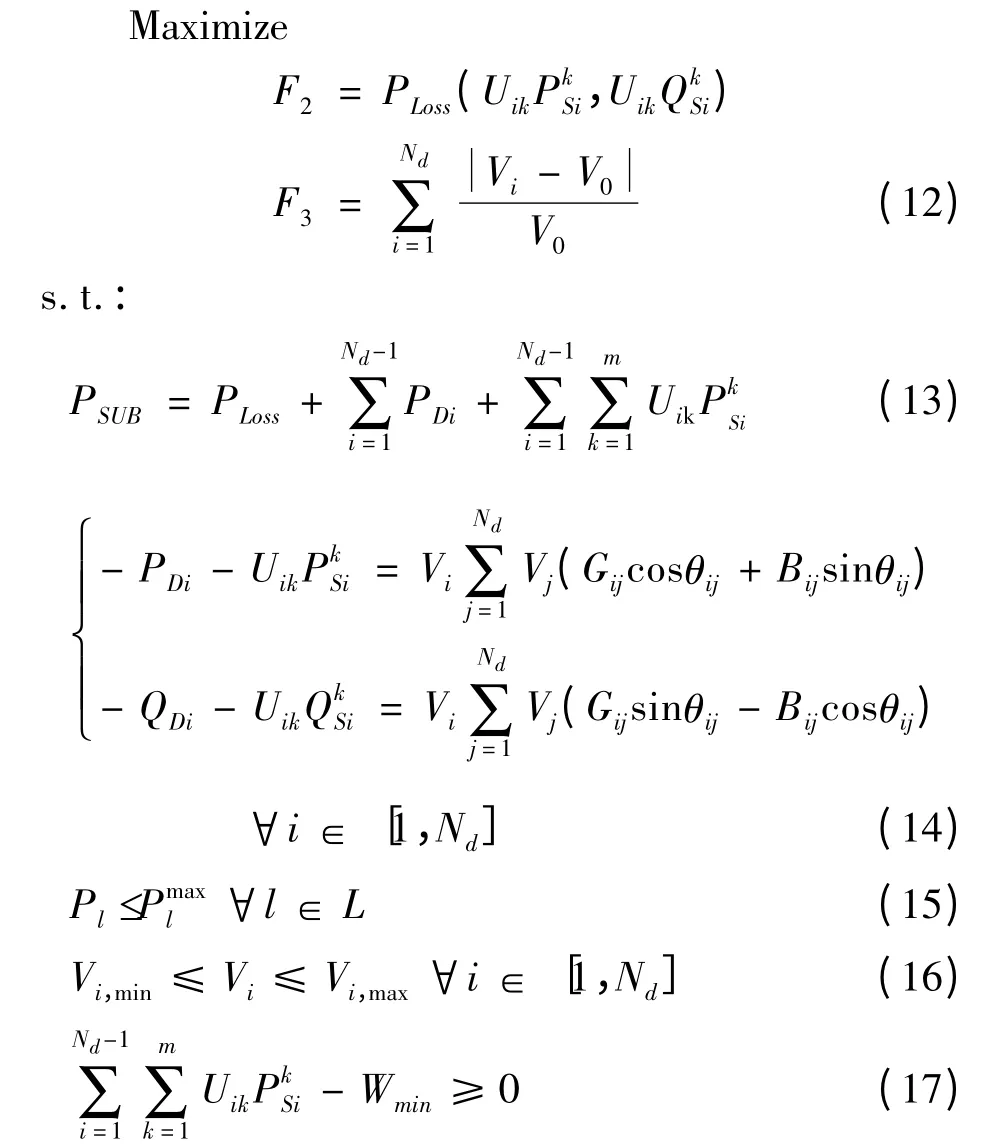
式(13)是充电设施的功率平衡约束，约束(14)是整个配电系统的潮流方程等式约束;(15)和(16)表示的是线路和节点的功率和电压约束;(17)表示的是EV 充电设施的总充电功率不应小于EV 的最小功率需求。

(3)多目标优化问题的简化处理与求解方法。上面给出了EV 充电设施规划的3 个优化目标。可以通过赋予权重的方式将多目标优化问题转化为单目标优化问题［10］:

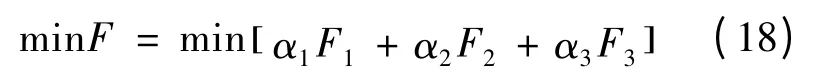
式中:α1，α2和α3为3 个目标的权重。权重的设定往往具有一定程度的主观性，需要根据实际情况进行权衡。由于3 个目标函数的量纲不同，需要对其进行归一化处理［11］，这里采用基于最大最小值的归一化方法［12］。这种方法需要首先求出各个目标函数各自的最大值Fk，max(x)和最小值Fk，min(x)(k=1，2，3)，然后用下式进行归一化:

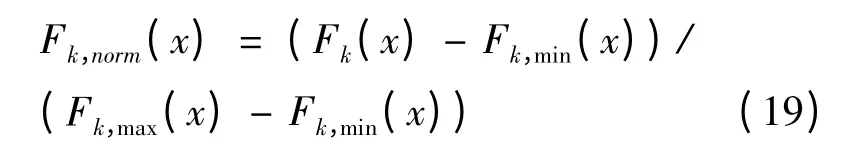
式中:Fk，norm(x)是归一化之后的目标函数。

经过如此转化之后得到的优化模型便可用现有的多种优化方法求解，本文采用了粒子群算法。

3 基于DEA 的充电设施多阶段规划

3.1 充电设施多阶段规划问题的DEA 描述

可以预期EV 在未来会得到快速发展，但其发展过程具有很强的不确定性。最主要的不确定性包括EV 发展类型、充电站/换电站、快充/慢充类型、负荷地理分布和EV 地理分布等。如果在EV 充电设施规划过程中不对这些不确定性给予合理考虑，则规划结果就可能有很大的风险。此外，在EV 充电设施规划中需要综合考虑交通系统、电力系统和负荷特征等多个方面。这样，规划决策时就需要考虑相互制约的多种要素。DEA 适合处理这一问题。

为便于描述，本节针对两阶段充电设施规划问题介绍所提出的方法，但方法框架适用于一般的情形。

为应对未来EV 发展中的不确定性，需要评估第1 阶段规划方案抵抗不确定性的能力。针对两阶段充电设施规划问题，可形成DEA 的输入输出，如表1所示。输入x 为第1 阶段的不同规划方案目标函数值，输出y 为下阶段各场景下的规划目标函数值。因此，评估效率值Ek的大小表征在不同发展场景下，第1 阶段规划方案的有效性。效率值最高的规划方案，不但能够在第1 阶段相对于其它规划方案具有较好的规划目标，而且对下阶段各种发展场景而言，均是较为适用的规划方案，能够较好抵御未来发展的不确定性。

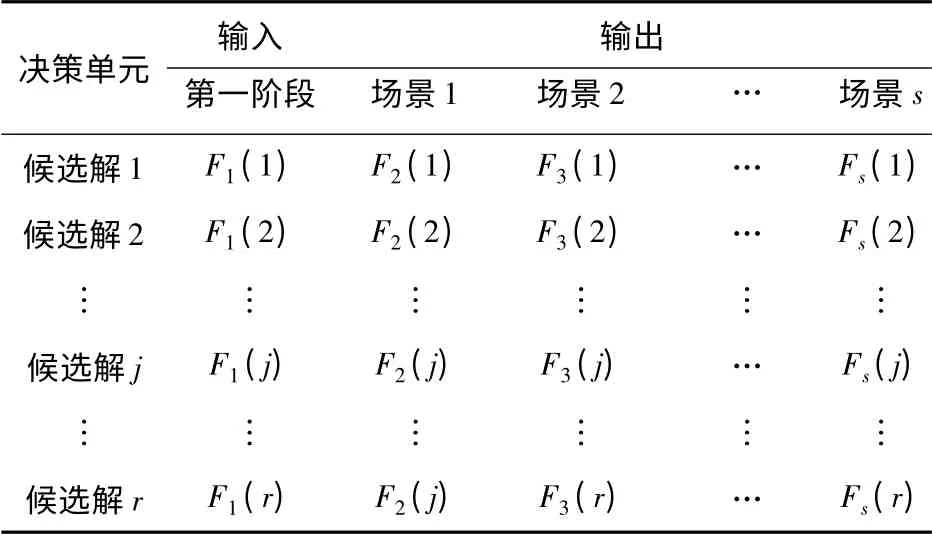
表1 EV 多阶段规划决策单元输入输出Tab.1 Inputs and outputs of multi-stage EV planning decision－making units

3.2 第2 阶段场景设置方法

前已述及，充电设施规划面临着多种不确定性。因篇幅所限，这里主要考虑3 种不确定性因素:充电设施类型的不确定性、充电负荷在配电系统中分布位置的不确定性和EV 车流在交通系统中分布不确定性。

(1)充电设施类型的不确定性。对EV 充放电控制的研究已引起广泛关注。EV 车主一般希望充电时间尽可能短，这样就需要快速充电站。对于EV 插入式充电模式，由于EV 的使用具有很强的随机性，这样对EV 充放电集中控制就相当困难。考虑到这些挑战，EV 换电站的发展近年来很受推崇，尤其在人口密集的大城市。EV 换电站最突出的特点在于EV 电池可以在很短时间内进行更换，而对更换下来的电池，则易于采取集中式充放电管理和控制。

对于EV 采用快速充电还是换电模式，现在仍然有很大的争议。采用不同的模式，对EV 的发展会产生不同的影响。在快速充电站模式下，EV 充电过程简单直接，但是会影响EV 正常行驶，同时快速充电也会对电池寿命产生影响;而在换电站模式下，更容易对电池充放电过程集中控制，对EV 行驶过程的干扰也较少，但是换电设备技术和实施过程较为复杂，换电设施投资成本也较大。因此，未来EV 充电设施的发展模式存在着很大的不确定性。

(2)充电负荷在配电系统中分布位置的不确定性和EV 车流在交通系统中分布不确定性。未来电力系统的负荷在空间上的发展和增长具有不确定性。负荷分布和人口分布、工业设施发展、居民区位置等诸多因素有关，受城市未来发展规划的影响较大。同样，EV 车流分布也受这些因素的影响和制约。居民区和商业区、工业区的位置在很大程度上会影响EV 车主的行驶行为，进而影响EV 车流在交通系统中的分布。

EV 车流在交通系统中的分布情况可以用交通系统的节点重要度来表征。节点重要度表示节点吸引车流量的能力。重要节点一般包括超级市场、工厂、居民区等。这些节点吸引车流量的能力比一般节点要强。

需要指出，虽然本节中只考虑了EV 充电设施规划中所面临的3 个方面的不确定性因素，但所采用的方法可以容纳一般情形。

4 算例分析

4.1 研究系统与参数设置

以图2 和图3所示的一个含有33 节点配电系统和25 节点交通系统的算例为例来说明所提出的方法。交通节点1－25 和配电系统的1－25 节点在地理位置上是重合的。配电系统的节点26与上级电力系统相连。系统详细参数可参见文献［13］。

图2 33 节点配电系统和25 节点交通系统示意图Fig.2 Test system with 33-node distribution system and 25-node traffic network

该系统的发展可分为2 个阶段，即阶段1 和阶段2，如图3所示。其中，区域1 和区域2 的发展具有不确定性。已知未来将会在配电系统中规划一个居民区和一个工业区，但居民区和工业区的位置尚不确定。基于已知信息，规划者定义了规划位置的两种场景。在场景1 中，配电系统节点26－33 将会发展为居民区，配电系统8－18 节点将会发展为工业区。在场景2 中，配电系统8－18 节点将会发展为居民区，配电系统节点26－33将会发展为工业区。

配电系统未来发展的不确定性将会产生多方面的影响。首先，配电系统未来发展属性的不同会影响负荷分布:一般而言，工业区的负荷要高于居民区的负荷。另一方面，配电系统未来发展属性的不同会影响EV 在交通系统中的分布:居民区吸引交通流量的能力往往要高于工业区。如文献［13］所述，节点吸引交通流量的能力可以用节点在交通系统中的权重W 来表示。重要节点(超市或者居民区所在位置)要比普通交通系统节点能够“吸引”更多的车流，其交通权重也就应该给定的较高。负荷和交通权重在第二阶段不同场景下的增长情况如表2所示。

由于EV 技术发展的不确定性，未来EV 充电设施的发展可能以换电站为主，也有可能以快速充电站为主。快速充电站和换电站的技术细节如表3所示。

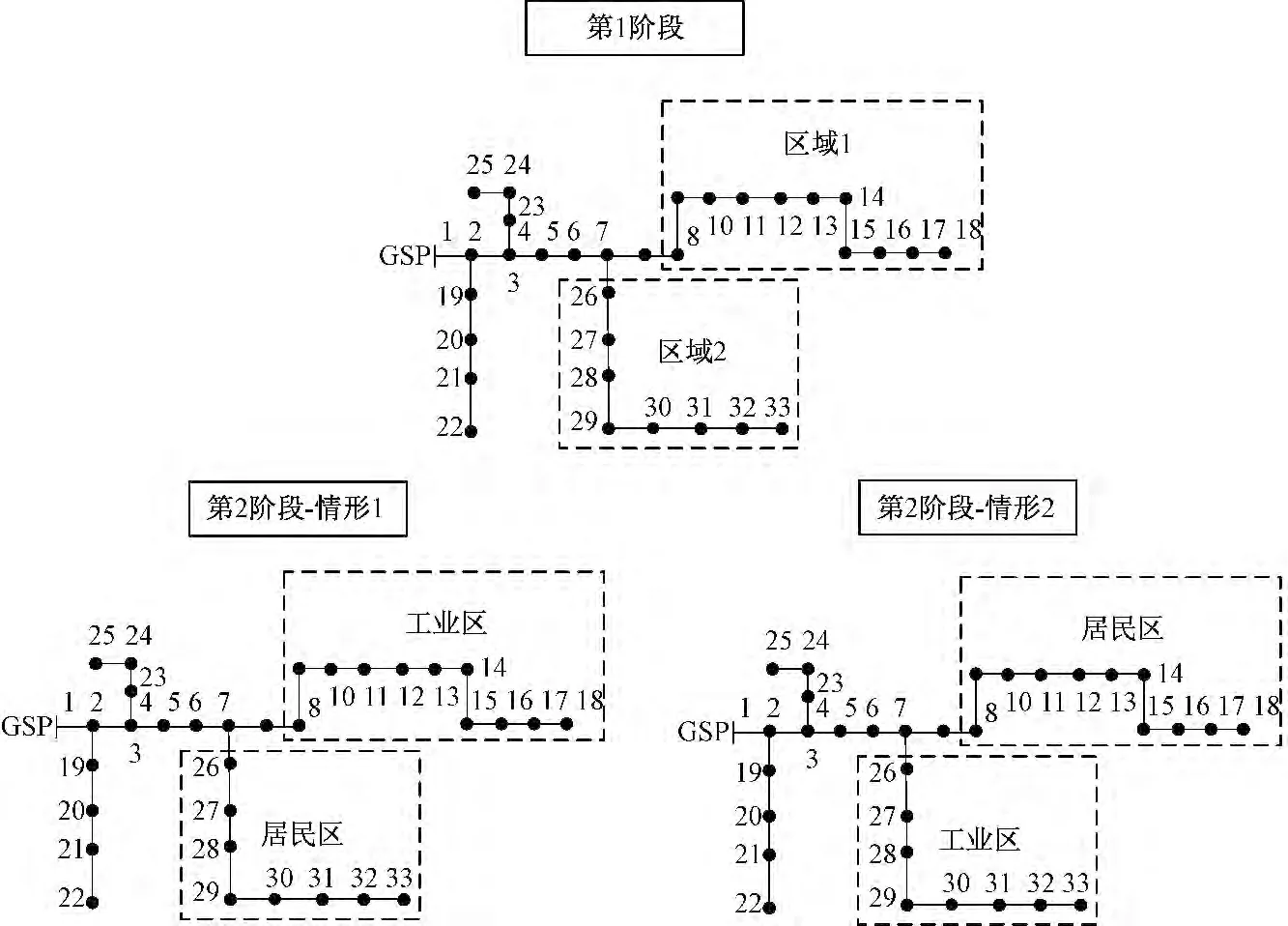
图3 配电系统充电设施两阶段规划Fig.2 Charging facility two－stage planning in a distribution network

表2 第二阶段负荷和交通权重增长率Tab.2 Increasing rate of loads and traffic weights in stage 2

表3 充电设施模型Tab.3 Models of Charging facilities

在第1 阶段规划中，快速充电站和换电站都是规划者的可行选择。然而，随着技术的发展，在第2 阶段规划中充电设施可能发展为以快速充电站为主，或者以换电站为主。因而关于充电设施类型，第2 阶段设置了A 和B 两种场景。在场景A 中，充电设施以发展快速充电站为主，即候选充电设施类型为快速充电站，并按额定功率不同分为I-IV 4 种。在场景B 中，充电设施以发展换电站为主，即候选充电设施类型为换电站，并按额定功率的不同分为I-IV 4 种。

综上所述，由于未来配电系统发展和充电设施技术发展存在的不确定性，第2 阶段的充电设施规划面临4 种不同场景:即场景1A，场景1B，场景2A 和场景2B。规划者期望规划方案不仅在第1 阶段的目标值较优，同时第1 阶段的规划结果能够有效应对第2 阶段配电系统发展的不确定性和充电设施发展的不确定性。换言之，规划者期望找到一个鲁棒性较强的第1 阶段充电设施规划方案，以有效应对下1 阶段的不确定因素

4.2 阶段1 规划

采用粒子群算法在Matlab 环境下进行仿真研究。假定第1 阶段只规划充电站而没有规划换电站。充电站规划的目标是最小化配电系统网络损耗和降低节点电压偏移，同时最大化EV 充电站的服务能力。需满足的约束包括线路潮流约束、节点电压约束，功率平衡约束。粒子群算法的种群规模给定为100，迭代次数为1 000。为保证结果合理，进行了10 次重复计算。表4 列出了第一阶段充电站规划最好的4 组结果。第2 阶段不同场景的充电设施规划(阶段2 情形1 和阶段2 情形2)将在这4 组结果的基础上进行。

表4 阶段1 最好的4 个规划方案Tab.4 The best four planning candidates in stage 1

4.3 阶段2 规划

采用粒子群算法，分别计算第一阶段最好的4 个规划方案(a～d)在第2 阶段4 种情形(1A，2A，1B 和2B)下的规划结果。第1 阶段的每个规划方案在第2 阶段每个情形下计算50 次，每次的迭代次数给定为1 000 次。其它粒子群算法的计算参数与阶段1 相同。获得的最好4 组结果如表5所示。在考虑第2 阶段规划所面对的不确定性的情况下，第1 阶段的最终规划方案应当统筹考虑阶段1 和阶段2 的需求。如表5所示，如果场景1A 出现，则最好的规划方案发展自第1 阶段的b 规划方案，而b 规划方案在第一阶段中并不是最优的(期目标函数不如规划方案a)。而当场景2A，1B 或2B 出现时，最好的规划方案均发展自第1 阶段的a 规划方案。

表5 不同情形下阶段2 最好的4 组规划方案Tab.5 The best planning schemes under different scenarios of stage 2

4.4 基于DEA 评估的第一阶段最优规划方案

用超效率DEA 计算第一阶段4 个候选规划方案(方案a～d)的效率值。输入x 为第1 阶段的某规划方案的目标函数值，输出y 为下阶段各场景下的规划目标函数值。目标是最大化规划方案的效率值。输出y1，y2，y3和y4分别是未来第2 阶段4 种场景1A，2A，1B 和2B 的目标函数值的倒数乘以10，表示每个方案的输入和输出值。

表6 列出了DEA 评估结果。因为方案a 和b的DEA 有效值都大于1，这两种规划方案都是可行的。方案a 的效率值高于方案b，这说明方案a是更好的规划方案。方案c 是效率值最低的规划方案。这样，方案a 是第1 阶段最好的规划解，应当被确定为阶段1 的最终规划方案。

表6 输入输出及DEA 评价结果Tab.6 Inputs，outputs and DEA evaluation results

5 结论

本文对考虑不确定性因素的充电设施多阶段规划问题进行了研究，建立了多目标优化模型，综合考虑了充电设施规划中配电系统和交通系统的相关要求和约束。建立了基于场景评估的两阶段充电设施规划模型，计及了未来充电技术发展选择、电力负荷分布与EV 车流分布等多种不确定性因素，提出了基于DEA 的充电设施规划方案评价方法。算例计算结果表明，DEA 可以辅助决策者确定最优规划方案，且如此获得的规划方案不仅可以满足现阶段要求，也能应对未来伴随电力系统发展和EV 技术发展而产生的多种不确定性因素，具有较好的鲁棒性。

［1］Amoli M E，Choma K，Stefani J.Rapid-charge electric-vehicle stations［J］.IEEE Trans on Power Systems，2010，25 (3):1883－1887.

［2］任玉珑，史乐峰，张谦，等.电动汽车充电站最优分布和规模研究［J］.电力系统自动化，2011，35(14):53－57.

［3］刘志鹏，文福拴，薛禹胜，等.电动汽车充电站的最优选址和定容［J］.电力系统自动化，2012，36(3):54－59.

［4］Hajimiragha A H，Caizares C A，Fowler M W，et al.Optimal transition to plug－in hybrid electric vehicles in Ontario，Canada，considering the electricity－grid limitations［J］.IEEE Trans on Power Systems，2010，57(2):690－701.

［5］Hajimiragha A H，Caizares C A，Fowler M W，et al.A robust optimization approach for planning the transition to plug-in hybrid electric vehicles［J］.IEEE Trans on Power Systems，2011，26 (4):2264－2274.

［6］Masoum A S，Deilami S，Moses P S，et al.Smart load management of plug－in electric vehicles in distribution and residential networks with charging stations for peak shaving and loss minimisation considering voltage regulation［J］.IET Generation，Transmission and Distribution，2011，5 (8):877－888.

［7］Charnes A，Cooper W W，Rhodes E.Measuring the efficiency of decision making units［J］.European Journal of Operational Research，1978，2 (2):429－444.

［8］Thanassoulis E.Introduction to the theory and application of data envelopment analysis［M］.Norwell，MA:Kluwer，2001.

［9］Zhan F.Three fastest shortest path algorithms on real road networks:data structures and procedures［J］.Journal of Geographic Information and Decision Analysis，1998，1 (1):70－82.

［10］Bayón L，Grau J M，Ruiz M M，et al.The exact solution of the environmental/economic dispatch problem［J］.IEEE Trans on Power Systems，2012，27 (2):723－731.

［11］Xu Z，Dong Z Y，Wong K P.A hybrid planning method for transmission networks in a deregulated environment［J］.IEEE Trans on Power Systems，2006，21 (2):925－932.

［12］Yang F，Kwan C M，Chang C S.Multiobjective evolutionary optimization of substation maintenance using decision－ varying Markov model［J］.IEEE Trans on Power Systems，2008，23 (3):1328－1335.

［13］王辉，王贵斌，赵俊华，等.考虑交通网络流量的电动汽车充电站规划［J］.电力系统自动化，2013，37 (13):63－69.