一类共形平坦的(α，β)-度量的研究

程新跃，李海霞

(重庆理工大学数学与统计学院学院，重庆 400054)

芬斯勒几何中有很多重要的非黎曼几何性质。一个是基本的几何量——嘉当张量C，另一个就是由Busemann-Hausdorff体积形式确定的挠率τ。对每个切空间中的挠率τ作竖直微分就得到了平均嘉当张量I∶=τykdxk。C、τ和I是一类将芬斯勒几何和黎曼几何区分开来的重要几何量。将C沿测地线进行微分得到Landsberg曲率L。τ沿测地线的水平斜变导数是S-曲率S∶=τ|kyk。将I沿测地线作水平斜变导数得到平均Landsberg曲率J∶=I|kyk。如果说黎曼曲率刻画了空间的形状，那么非黎曼几何量则描述了这个空间的色彩变化，所以芬斯勒空间是一个“充满色彩”的几何空间。研究发现:旗曲率与这些非黎曼几何量密切相关［8-9］。

通过上述定义可知:J/I可以看作是平均嘉当张量沿着测地线的相对变化率。芬斯勒流形M上的一个芬斯勒度量F如果满足J+cFI=0，则称它具有相对迷向的平均Landsberg曲率，这里c=c(x)是M上的标量函数。特别地，当c=0时，J=0，此时F称为弱Landsberg度量。许多芬斯勒度量满足J+cFI=0［8-10］。李本伶等［11］刻画了弱Landsberg的(α，β)-度量F，并给出了在流形维数大于2的情形中存在是弱Landsberg而非Landsberg度量的例子。本文针对文献［12］研究和刻画了具有相对迷向的平均Landsberg曲率的(α，β)-度量。本文首先研究了共形平坦的弱Landsberg的(α，β)-度量，并得到定理1。

定理1 芬斯勒流形M上任意共性平坦的弱Landsberg的(α，β)-度量一定是黎曼度量或闵可夫斯基度量。

进一步研究了共形平坦且具有相对迷向的平均Landsberg曲率的(α，β)-度量，得到定理2。

1 预备知识

设M是一个n维的光滑流形，TM是M上的切丛。芬斯勒度量F是TM上的函数，即 F∶TM→［0，∞)，且满足:①F在TM{0}上是光滑的;② 对任一点x∈M，Fx(y)∶=F(x，y)是TxM上的一个闵可夫斯基范数。称(M，F)是一个n维芬斯勒流形。

设(M，F)是一个芬斯勒流形，且

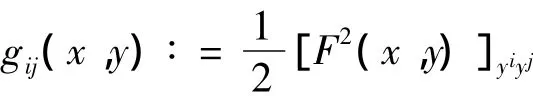
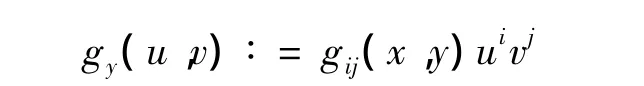
给定一个芬斯勒度量F，测地线可以由如下二阶常微分方程描述:

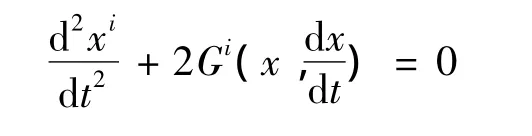
这里

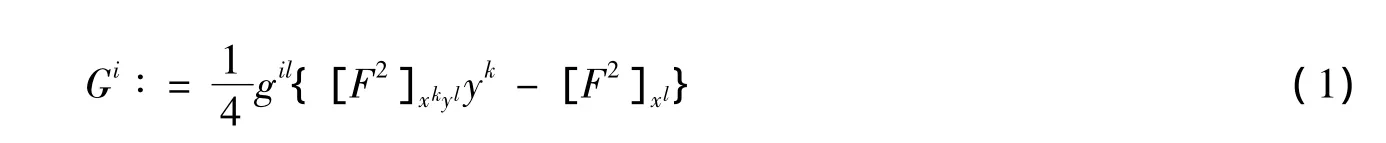
且(gij)=(gij)-1，Gi称作F的测地系数。

设

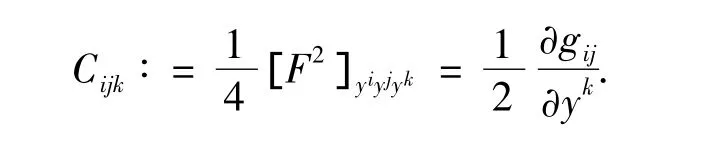
定义TM{0}上的双线性张量C∶=Cijk(x，y)dxi⊗dxj⊗dxk，称C为嘉当张量。平均嘉当张量I=Iidxi定义为

进一步有［8-9］

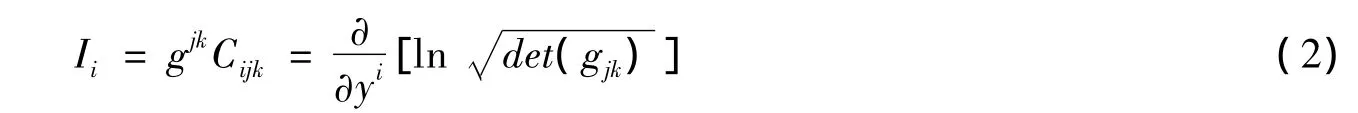
在 TM{0}上，Landsberg 曲率 L∶=Lijkdxi⊗dxj⊗dxk，Lijk∶=Cijk|mym。L 可以进一步表示为

满足Lijk=0的芬斯勒度量称为Landsberg度量。

平均Landsberg曲率J∶=Jidxi定义为

容易看出Ji=Ii|mym。满足J=0的芬斯勒度量F称为是弱Landsberg度量。更一般地，如果F满足J+cFI=0，那么称它为具有相对迷向的平均Landsberg曲率，这里c=c(x)是流形的上的标量函数。

流形M上的芬斯勒度量(α，β)-度量具有以下形式:

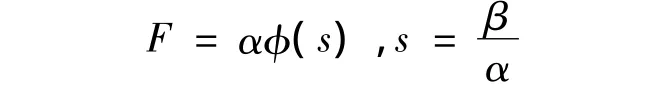
特别地，当φ=1+s时，F=αφ(β/α)是一个 Randers度量 F=α+β。我们用“|”表示关于 α的水平协变导数。

定义

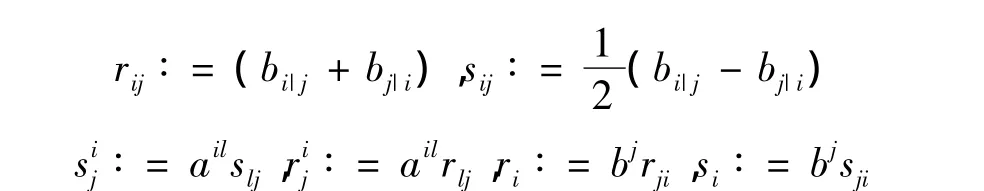
将F和α在相同坐标系下的测地系数分别记为Gi和Giα，则有［13］

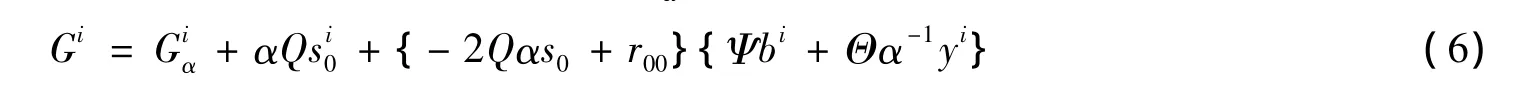
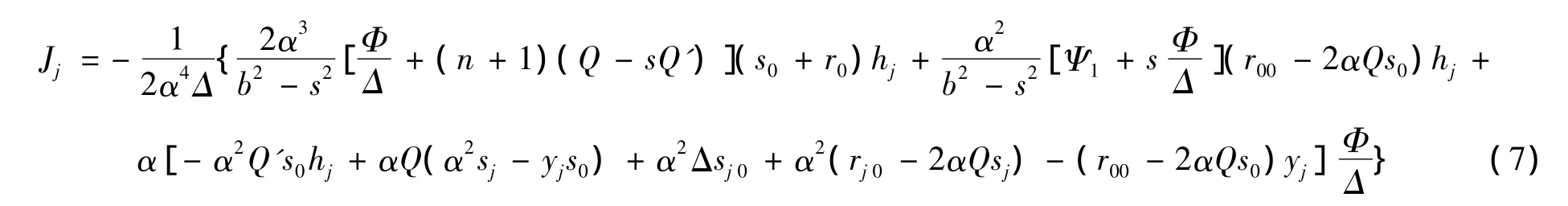
这里 yj=aijyi。

2 定理1的证明

现在证明主要定理。首先提出关于(α，β)-度量的平均嘉当张量的引理。

引理 1［12］对于(α，β)- 度量，平均嘉当张量

由Deicke定理，芬斯勒度量是黎曼度量，当且仅当I=0。由式(5)和φ(s)＞0，有φ(s)-sφ'＞0(|s|≤b＜b0)。因此，由引理1可以得到引理2。

引理2［12］(α，β)-度量F是黎曼度量，当且仅当 Φ=0。

令 J∶=Jjbj，由式(7)有引理 3。

引理 3［11］对(α，β)-度量，J可由式(9)给出:

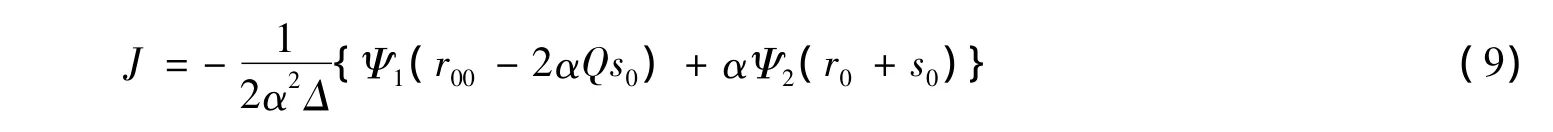
由式(7)和(8)可得［12］

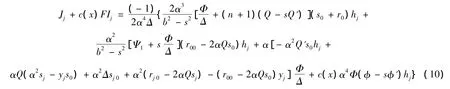
进一步地可得引理4和5。

引理4［14］(α，β)-度量是局部闵可夫斯基度量，当且仅当α是平坦的且bi|j=0(β关于α是平行的)。

引理5 如果φ=φ(s)满足Ψ1=0，那么F是黎曼度量。

证明 由 Ψ1=0，即，得到那么对|s|≤b ＜ b0，是一个常数。令s=b得到Λ(s)=0。因此Λ(s)≡0，得Φ=0。由引理2知F是黎曼度量。

如果φ=φ(s)满足b2Q+s=0，得到这里k是一个与 s无关的常数。所以有引理6。

引理6 如果φ是关于s的多项式，那么b2Q+s≠0。

现在假设F=αφ(β/α)是共形平坦的，即F共形相关于一个闵可夫斯基度量那么存在流形上的一个标量函数σ=σ(x)使得=eσ(x)F。有

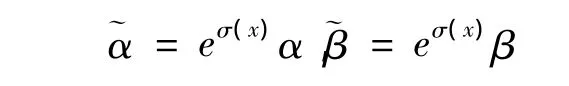
等价于

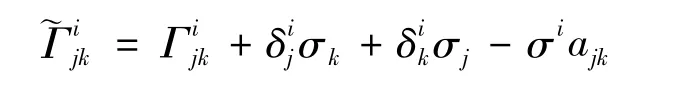
因此得到

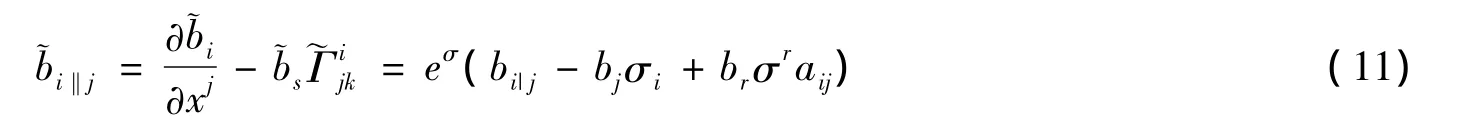
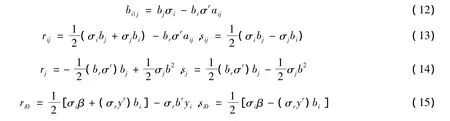
进一步有

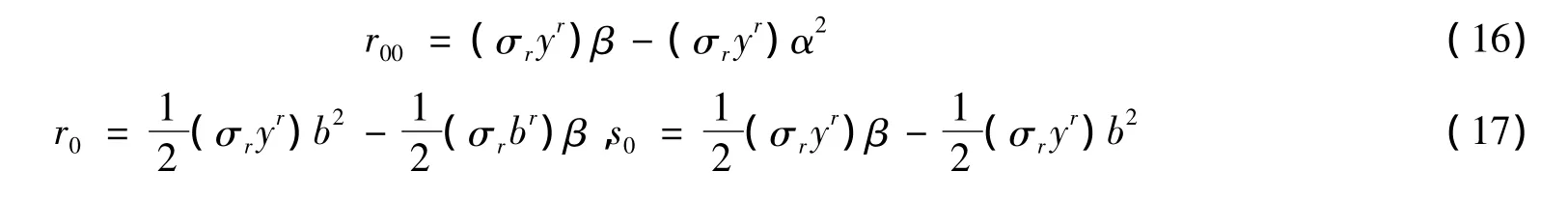
由式(17)很容易看出，对于共形平坦的(α，β)-度量，有

为了克服计算中的困难，在任意点x处取关于α的标准正交基，使得

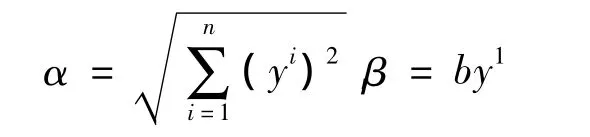
这里 b∶= ‖βx‖α，在 TxM 上作坐标变换［15］ψ∶(s，uA)→(yi)，可得

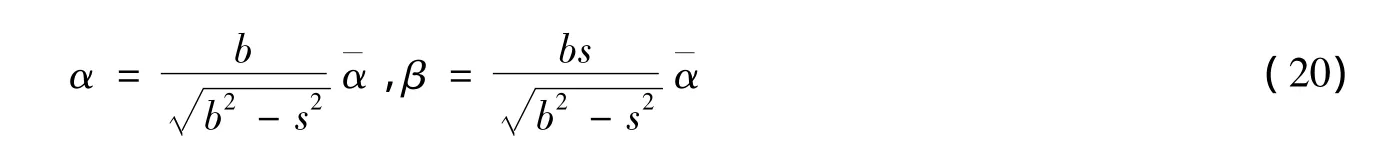
由式(13)～(17)、(19)、(20)有

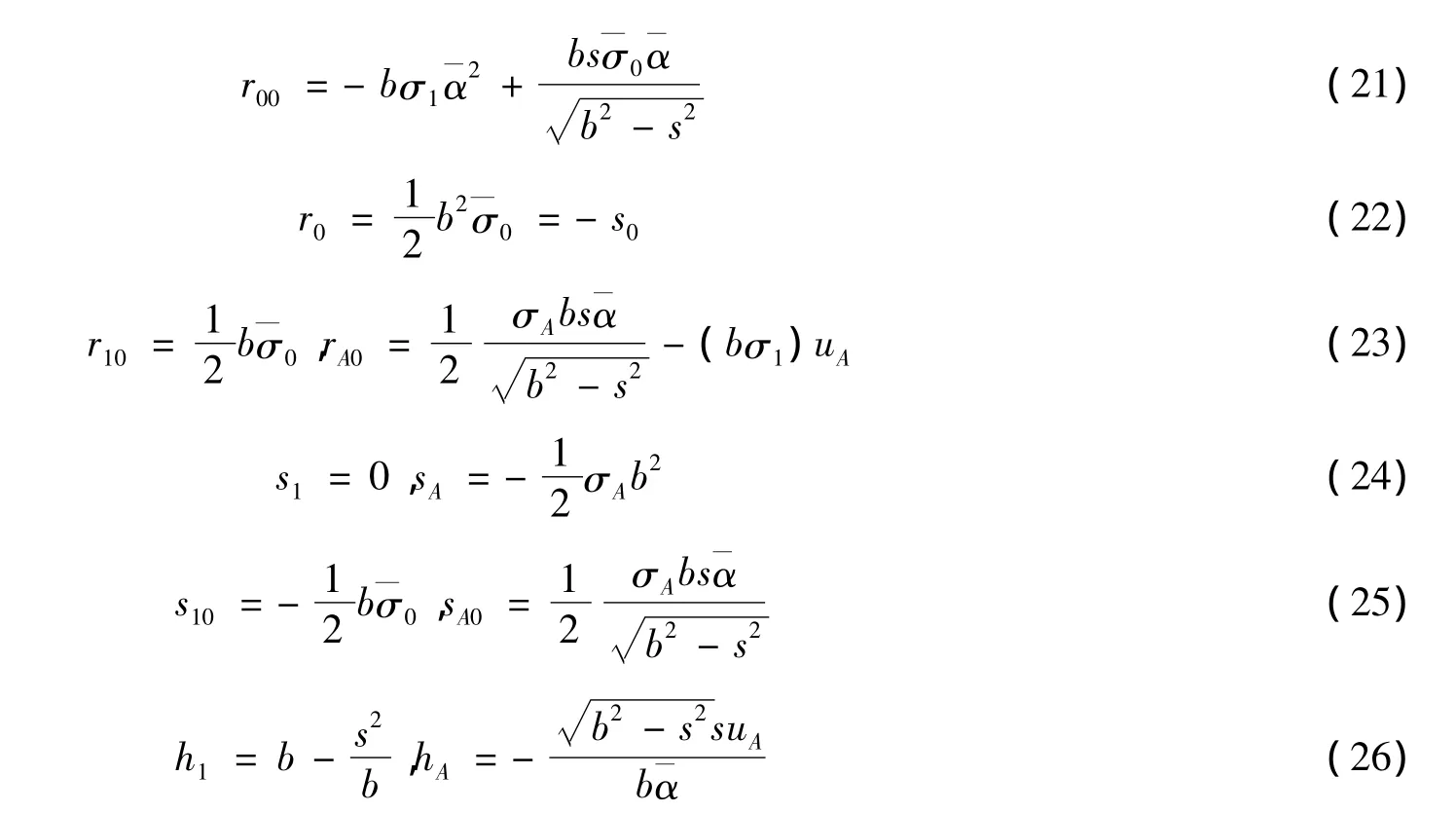
现在证明定理1。

假设F是一个弱Landsberg度量，那么它满足J=0。把r0+s0=0代入式(9)中，得到Ψ1=0或r00-2αQs0=0。

如果Ψ1=0，由引理5可得F是黎曼的。

如果 r00-2αQs0=0，由式(20)～(22)可得

进一步可得

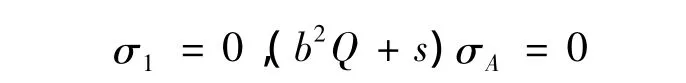
如果φ=φ(s)满足b2Q+s=0，由引理6的证明知F是黎曼的。如果b2Q+s≠0，那么σA=0，加上前面证明的σ1=0可得σ=常数。所以F是闵可夫斯基度量。

3 定理2的证明

假设(α，β)-度量F共形平坦，且具有相对迷向的平均Landsberg曲率。由式(10)和r0+s0=0，可得

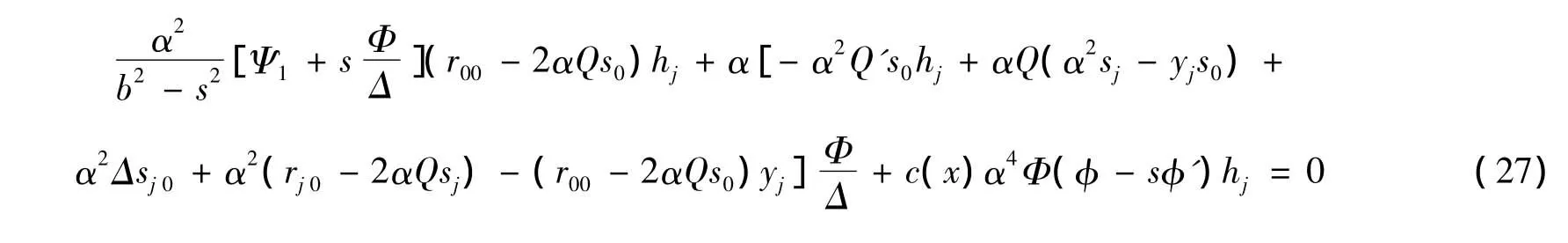
令式(27)中j=1，可得

把式(20)～(26)代入(28)中，并乘以2Δ(b2-s2)5/2，可得

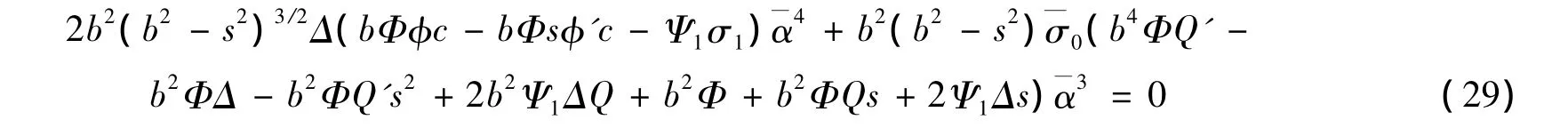
由式(29)知

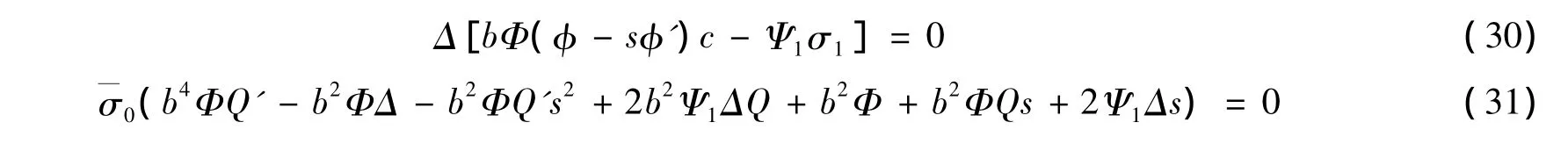
根据 Δ =Q'(b2-s2)+sQ+1，式(31)可简化为(b2Ψ1ΔQ+Ψ1Δs)=0，即

令式(27)中j=A，可得

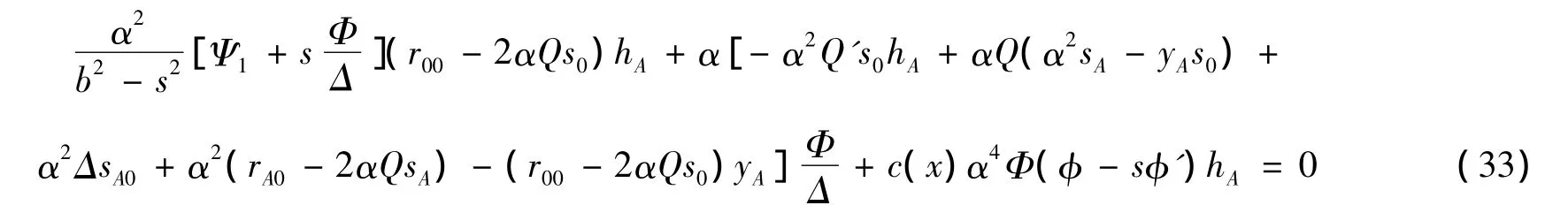
将式 (20)～(26)代入(33)，使用与j=1情形中同样的方法，得到

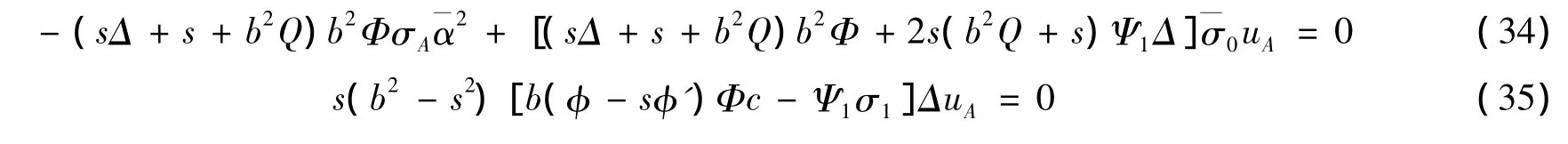
很容易看出式(35)和(30)相同。进一步地，将式(34)乘以uA，得到

可以看出式(36)等价于式(32)。

综上，共形平坦且具有相对迷向平均Landsberg曲率的(α，β)-度量满足式(30)和式(32)。

由引理6知b2Q+s≠0。由式(32)可知，Ψ1=0或σA=0。如果Ψ1=0，由引理5知F是黎曼的。根据引理2，Φ=0，因此式(30)成立。如果 Ψ1≠0，那么 σA=0。接着，从式(30)出发，证明当 Ψ1≠0时，σ1=0。

由假设知φ(s)是关于s的多项式。设

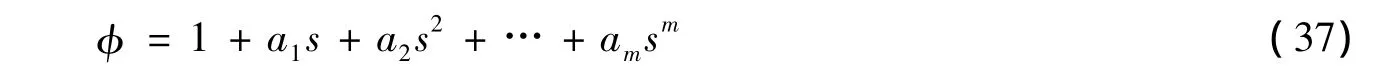
这里 a1，a2，…，am是跟 s无关的数，并且am≠0。

首先，考虑在式(38)中m＞1的情形。简化式(30)，并乘以Δ2，得

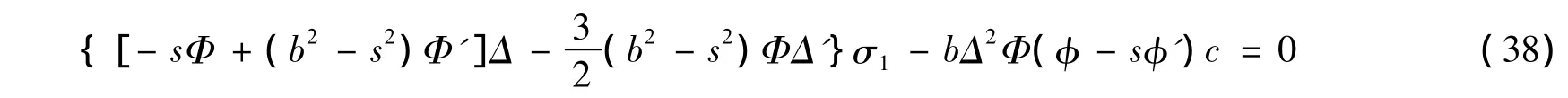
将式(37)代入式(38)，并乘以2(-1+a2s2+2a3s3+…+(m-1)amsm)，通过Maple程序，得到

这里k1、k2、k3是跟m无关的常数。例如

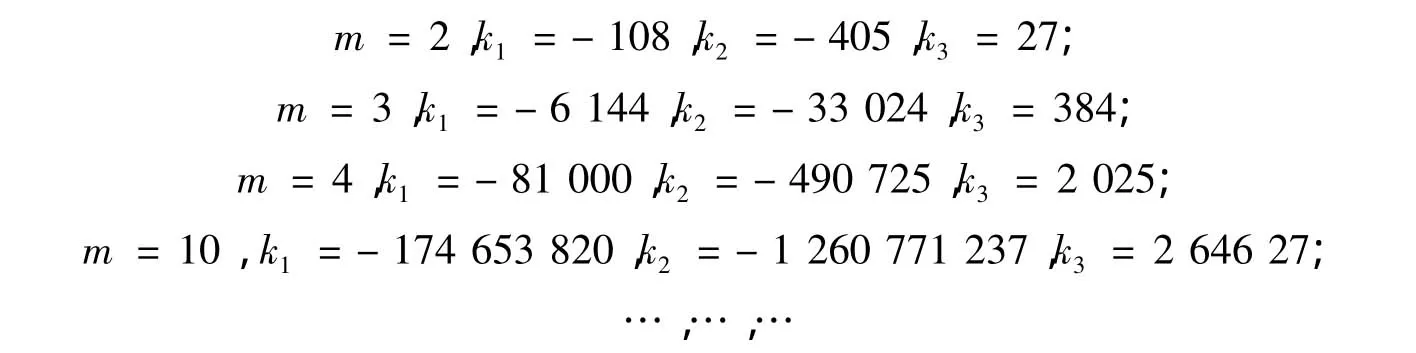
当 m=100 时，k1=-19 794 060 593 980 200，k2=-156 773 780 240 111 397，k3=2 969 406 029。ηi(1≤i≤7)是关于 a1、a2、a3和 a4的多项式，且与 s和 m 无关，

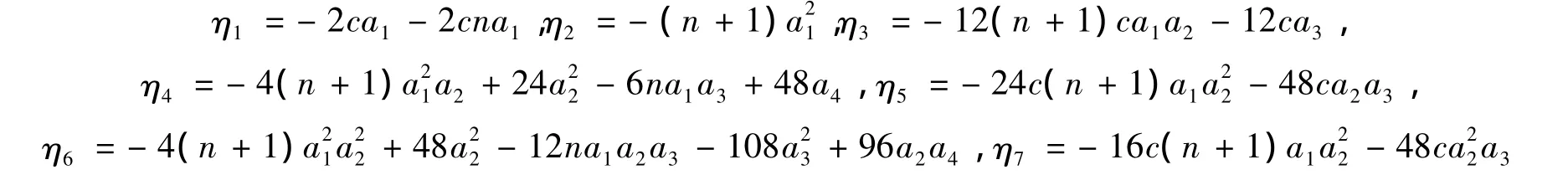
从式(40)中可以看出k1nbca=0，因此有c=0。由式(30)可得σ1=0。加上前面证明的σA=0，可知σ是个常数，则F是一个闵可夫斯基度量。

其次，考虑式(37)中m=1的情形。在这种情况下，F是一个Randers度量。在文献［10］中，笔者和沈忠民教授已经证明了Randers度量F=α+β具有相对迷向平均Landsberg曲率，当且仅当它具有迷向S-曲率(S=(n+1)cF)而且β是闭的。进一步地，在文献［5］中，证明了共形平坦且具有几乎迷向的S-曲率一定是黎曼度量或者闵可夫斯基度量。因此，对于Randers度量定理2是成立的。至此完成了定理2的证明。

［1］Bacso S，Cheng X.Finsler conformal transformalations and the curvature invariances［J］.Publ Math Debrecen，2007，70(1/2):221-231.

［2］Ichijy Y，Hashuiguchi M.On the condition that a Randers space be conformally flat［J］.Rep Fac Sci Kagoshima Univ，1989，22:7-14.

［3］Kikuchi S.On the condition that a Finsler space be conformally flat［J］.Tensor N S，1994，55:97-100.

［4］Hojo S，Matsumoto M，Okubo K.Theory of conformally Berwald Finsler spaces and its applications to(α，β)-metrics［J］，Balkan J.of Geometry and Its Applications，2000，5(1):107-118.

［5］Kang L.On conformally flat Randers metrics(in Chinese)［J］，Sci Sin Math，2011，41(5):439-446.

［6］田艳芳，程新跃.一类具有指数形式的Einstein(α，β)-度量［J］.重庆理工大学学报:自然科学版，2011，25(4):112-116.

［7］Chen G，Cheng X.An important class of conformally flat weak Einstein Finsler metrics［J］.International Journal of Mathematics，2013，24(1).

［8］Cheng X，Mo X，Shen Z.On the flag curvature of Finsler metrics of scalar curvature［J］.London Math So，2003，68(2):762-780.

［9］Shen Z.On a class of Landsberg metrics in Finsler Geometry［J］.Canadian Journal of Mathematics，2009，61(6):1357-1374.

［10］Cheng X，Shen Z.Randers metrics with special curvature propertities［J］.Osaka J Math，2003，40:87-101.

［11］Li B L，Shen Z.On a class of weak Landsberg metrics［J］.Science in China Series A，2007，50(1):75-85.

［12］Cheng X，Wang H，Wang M.(α，β)-metrics with relatively isotropic mean Landsberg curvature［J］.Publ Math Debrecen，2008，72(3/4):475-485.

［13］Chern S S，Shen Z.Riemann-Finsler Geometry，Nankai Tracts in Mathematics［M］.Singapore:World Scientific，2005.

［14］Antonelli P L，Ingarden R S，Matsumoto M.The Theory of Sprays and Finsler Spaces with Applications in Physics and Biology［M］.New York:Springer，1993.

［15］Cheng X，Shen Z.A class of Finsler metrics with isotropic Scurvature［J］.Israel Journal of Mathematics，2009，169(1):317-340.