基于模糊控制的火箭伺服系统频域控制设计方法

钱昌年 傅俊勇

上海航天控制技术研究所，上海200233

火箭伺服系统是火箭推力矢量控制系统的执行端，根据箭载计算机的控制指令改变发动机摆角，对火箭姿态进行调整。某新型大推力火箭发动机柔度大、谐振频率低，作为火箭伺服系统的负载，其谐振特性给伺服系统控制算法的设计带来了困难。具有低机械谐振频率的系统，工程中常使用陷波滤波器进行校正［1－2］，陷波滤波器在指定的频带产生幅值凹谷，从而抵消机械谐振。文献［3］针对某型号火箭伺服系统的低频谐振和2个谐振点问题设计了双陷波控制算法，消除了谐振的影响，但双陷波滤波器在抑制谐振峰与改善系统相位特性之间存在难以调和的矛盾，对系统相位特性的改善有限。

针对双陷波滤波器的不足，本文引入模糊控制的思想，设计了一种能够对系统频域特性进行补偿的模糊控制算法，有效改善了系统的相位特性，提升了系统频率特性。

1 问题描述

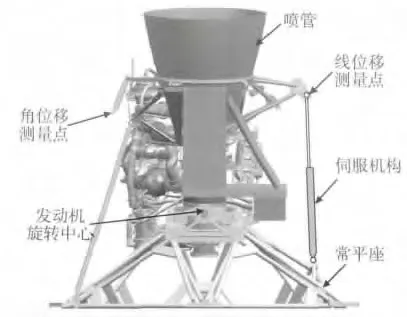
图1 某型火箭伺服系统半实物模拟试验台

某型火箭伺服系统如图1 所示，伺服机构采用铰链与发动机喷管和发动机常平座连接，发动机可以绕旋转中心自由摆动。在系统工作过程中，伺服机构接收指令改变作动筒伸缩量，驱动发动机改变喷管摆角，从而改变发动机推力方向以调整火箭姿态。

伺服系统的控制原理如图2 所示，线位移为机构作动筒的伸缩量，角位移为发动机摆角，线位移和角位移的测量位置见图1。控制信号施加在伺服机构，反馈信号来自线位移测量点，用于评估系统动态特性的信号来自角位移测量点。

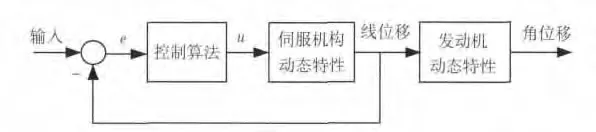
图2 伺服系统控制原理

系统的性能指标和采用比例控制算法测试得到的系统频率特性如图3 所示(频率特性通过定点扫频方法测得)。性能指标要求在0 ～8Hz 时，系统的幅值不得大于指定值，同时不得小于－3dB;在8Hz之后，系统的幅值不得大于指定值;在0 ～6.28Hz时，系统的相位不得小于指定值。

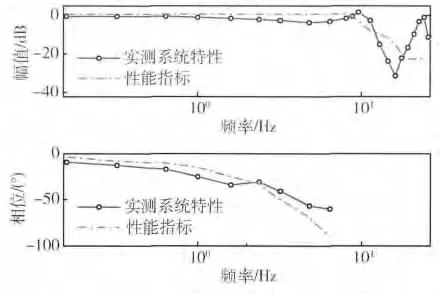
图3 采用比例控制的系统实测特性

从幅频特性看，系统在10Hz 和24Hz 附近存在2个明显的谐振峰，相关试验和分析结果表明幅频特性的2个谐振峰由发动机刚度不足造成;从相频特性看，系统在低频段的相位明显滞后于性能指标。可见，必须采用有效的控制算法对系统的频率特性进行校正，以使系统频率特性满足性能指标。文献［3］采用了双陷波滤波器控制算法(如图4 所示)，使用2个串联的陷波滤波器对应抵消了系统的2个低频谐振峰，目前该算法被应用于某型伺服系统的试样产品上。

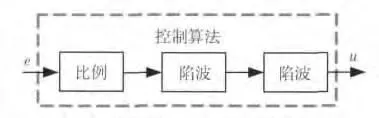
图4 双陷波滤波器控制框图

然而陷波滤波器给系统的相位带来了不利影响(如图5 所示)，在调试过程中必须依靠增大比例系数来改善相位滞后，比例系数变大又会使系统的幅频特性超过性能指标。双陷波控制算法在抑制谐振峰和改善相位滞后之间存在矛盾。

图5 采用双陷波滤波器控制的系统实测特性

2 模糊控制器设计

为了进一步提高伺服系统的动态性能，使系统满足性能指标并且相对指标具有一定裕量，本文设计了一种采用T－S 结构的模糊比例控制器。考虑伺服系统的低频谐振问题，所设计的控制器要使整个系统让低频信号无衰减地通过，而对于比较高频的信号适当加以衰减，在谐振点附近的频率成分，必须施加较强衰减。在控制律运行过程中，当输入信号中低频成分占主导时，控制器采用较大的比例系数，这样可以保证信号不受较大衰减，而且可以提高系统的相频特性，但为了保证少量的高频成分不会因谐振放大而导致低频成分被淹没，可以在控制算法中串联适当阶数的低通或陷波滤波器;当通过系统的信号中高频成分占主导时，控制器采用较小的比例系数，使高频信号得到较强衰减从而削弱谐振。根据上述规律，可以设计模糊控制算法，根据通过系统信号的频率成分实时改变控制器的比例系数和滤波参数。简单起见，本文设计的控制器只实时调节控制器的比例系数，串联一个固定参数的陷波滤波器。

一般情况下，系统的输入信号可以表示为

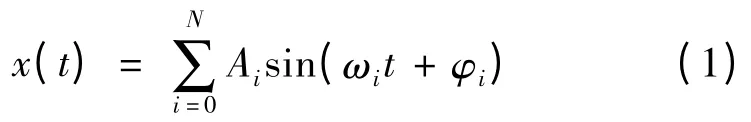
其中Ai，ωi和φi分别为不同频率成分的幅值、频率和相位。那么在［^t － τ ^t］时间段内高频成分和低频成分在整个信号中所占的比重可以表示为

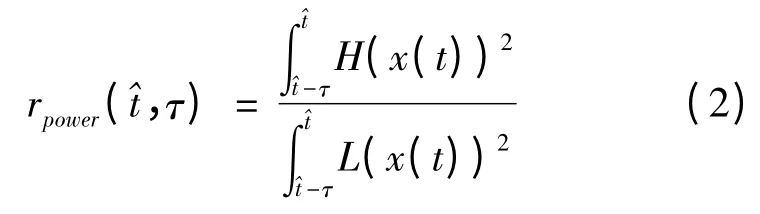
其中τ ＞0 ，根据实际需要确定;H(·)和L(·)分别为具有适当阶数的高通滤波器和低通滤波器，用于提取信号中的高频成分和低频成分(考虑到噪声影响，也可以将高通滤波过程省去，即式(2)中的分子项中直接对［x(t)］2积分)。式(2)中r 的物理意义为在时间段内信号x(t)中高频成分和低频成分的功率比(式中约去了系数1/τ)。考虑到式(2)中含有平方项，为了减少运算量，可以将信号成分比定义为

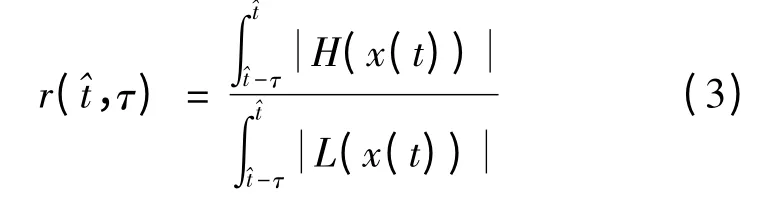
将式(3)写为离散形式，得到

其中，N ＞0 ，本文取N = 20 。根据上述方法建立的模糊控制器原理如图6 所示。相比于标准模糊系统，T－S 模糊系统具有更强大的函数能力［4－5］，故本文算法采用T－S 模糊系统实现。模糊算法输入为信号成分比r 和线位移误差e，但用于模糊规则判断的输入只有r，输出为控制信号u。设信号成分比r 的模糊化量为R (采用单值模糊化方法)，则模糊算法第i 条规则可以写为

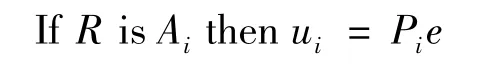
其中，Ai为定义在r 的论域上的模糊集合;Pi为比例系数。设模糊系统具有M 条规则，那么模糊算法的输出为

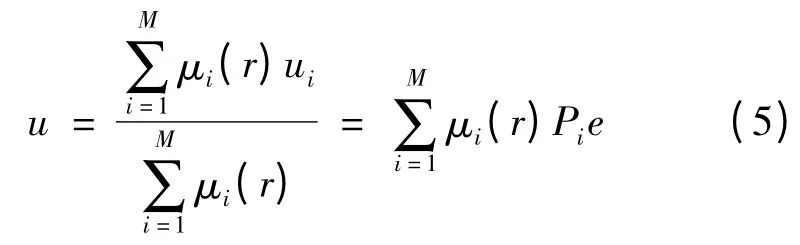
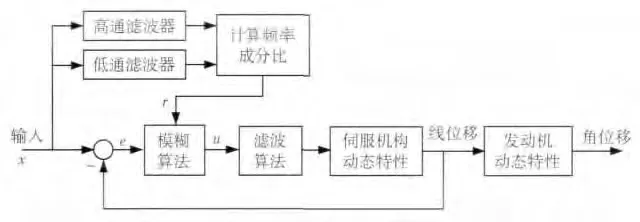
图6 模糊比例控制原理

经过分析和反复调试，最终确定的模糊算法隶属函数如图7 所示，输入值r 的论域被划分为5个模糊集合。在图7 中，对于任意输入值r*，最多存在2个模糊集合，r*对其隶属度μi(r*)＞0 ，并且这2个隶属度的和为1。

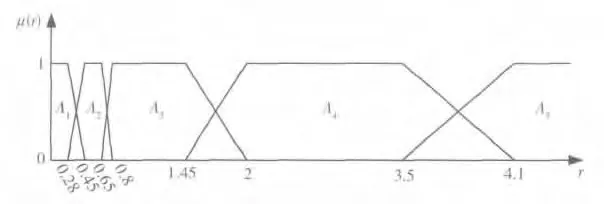
图7 最终确定的隶属函数

对应地，设计的模糊算法规则库由5 条规则组成，分别为

控制算法采用的高通滤波器，低通滤波器和陷波滤波器分别为

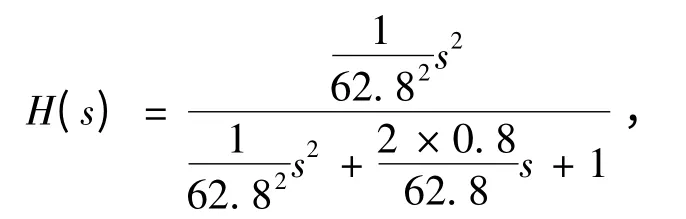
3 MATLAB 仿真

使用MATLAB/Simulink 建立伺服系统的模型(如图8 所示)，采用扫频方法测试模糊算法的有效性，仿真过程中仿真步长为1ms，求解算法为四阶Runge－Kutta 方法。

图8 仿真模型

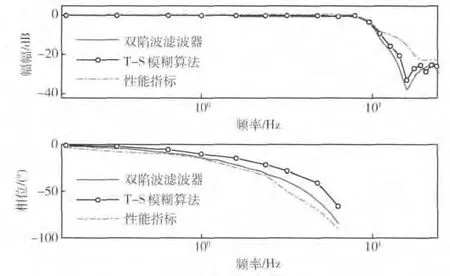
图9 T－S 模糊算法和陷波滤波器算法仿真结果

仿真结果如图9 所示，双陷波滤波器的模型仿真结果与试验结果(图5)的差异由仿真模型与实际系统的偏差造成，不影响T －S 模糊算法和双陷波滤波器算法进行比较。图9 中，双陷波滤波器和T－S模糊算法均能有效抑制发动机造成的低频谐振，二者均使系统的频率特性满足性能指标。从相频特性看，T－S 模糊算法使系统的相位滞后得到显著改善，尤其在性能指标要求范围的后半段，T －S模糊算法明显优于双陷波滤波器算法，二者对于系统相位的影响最大差别达到了18°。可见，T －S 模糊算法具有更好的控制效果。适度采用更高复杂度的模糊规则可以在更大程度上改善系统的动态特性，但过于复杂的控制规则会使控制器的运算量加大，所以对于T －S 模糊系统复杂度的确定应当综合考虑性能指标和运算成本。

4 结论

针对某型火箭发动机谐振频率低、伺服系统不易控制的问题，从频域角度出发设计了一种结合陷波算法的T －S 模糊控制算法，仿真结果表明该算法使伺服系统的频率特性得到改善，相比于现役的双陷波算法能够调和幅频特性与相频特性难以均衡调控的矛盾。该算法着眼于系统频域特性，将模糊的思想引入到了控制器频域设计，克服了传统模糊控制算法难以补偿系统频率特性的不足，具有一定工程参考价值。

［1］杨辉，范永坤，舒怀亮.抑制机械谐振的一种改进的数字滤波器［J］.光电工程，2003，31:30-39.(YANG Hui，FAN Yongkun，SHU Huailiang. An Improved Digital Filter for Restraining Mechanical Resonance Frequency［J］.Opto－Electronic Engineering，2003，31:30-39.)

［2］Soo-Chang Pei，Chien-Cheng Tseng. IIR Multiple Notch Filter Design Based on Allpass Filter［C］. IEEE TENCON Conference on Digital Signal Processing Applications，1996.

［3］张亮，傅俊勇. 一种适应大惯量偏心负载的伺服系统控制律设计［R］.上海航天控制技术研究所内部报告，2012.(ZHANG Liang，FU Junyong. A Kind of Control Law for Servo-system with Large Off-centered Load［R］.Shanghai Institute of Spaceflight Control Technology (Internal Report)，2012.)

［4］李洪兴.Fuzzy 控制的本质与一类高精度Fuzzy 控制器的设计［J］. 控制理论与应用，1997，14(6):868-872.(LI Hongxing. The Essence of Fuzzy Control and A Kind of Fine Fuzzy Controller［J］. Control Theory and Application，1997，14(6):868-872.)

［5］Wang L X. Fuzzy Systems Are Universal Approximators［C］. San Deigo:In Proc. of the 1stIEEE Conference on Fuzzy Systems，1992，3:1163-1170.