多目标系统最优控制方法研究*

杜振华 谌海云 曾 欢 石明江

1. 西南石油大学电气信息学院，成都610500

2. 中海油节能环保服务有限公司，天津300457

多目标系统最优控制主要研究存在多个目标泛函时，在给定的状态约束条件下寻求最优控制律并达到决策者所需的最优。在工程实际中，多个指标之间往往相互冲突、相互矛盾，一方利益的获得会导致另一方利益的受损。决策者则会通过自身的经验给予各个指标不同的权重。这种传统的设计方法偏离了实际数值意义上的最优。

从上世纪90年代起，一些学者提出了针对二次性能指标的多目标最优控制，诸如Khargnnekar 和Rotea 的凸优化方法［1］，Salukvadze 的向量值法［2］，Shtessel 的比例损耗原理及我国学者张成科的小波逼近法［3］。这些传统方法的数值计算十分复杂，且对问题性质有着要求。

进化计算的发展对复杂问题的寻优提供了有效方法，本文将现代控制论与多目标进化算法结合，通过构建免疫克隆选择算法求解多目标情况下的最优控制问题。并针对具有较多先验知识的决策者，提出了一种用层次分析法分配多目标之间权重的方法。

1 系统数学模型

随着空间技术的发展及最短时间问题的提出，最优控制理论逐渐发展起来，其基本数学模型如下:

一个被控系统可以用下式表征

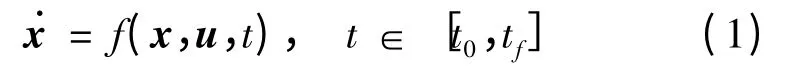
式中，x 描述被控对象的n个独立变量，u 为控制量，f(x，u，t)是描述被控对象动态特征的n 维矢值函数。则存在一个容许控制ui(t)，i = 1，2，…，r;ui(t)≤M，使得性能指标取极小。

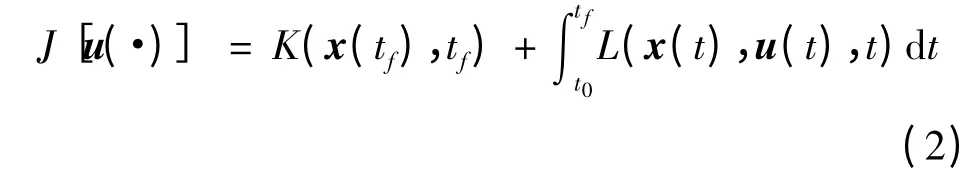
那么多目标的系统则表述为:

寻求最优控制律ui(t)，i = 1，2，…，r，同时使得如下指标取极小值

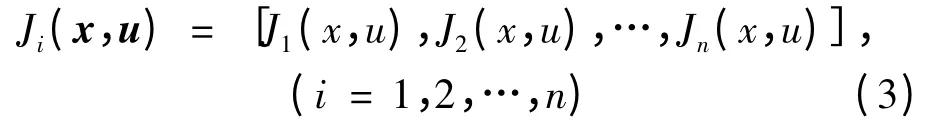
2 层次分析法

层次分析法(Analytical Hierachy Process，AHP)是一种整理和综合人们主观判断的客观分析方法，也是一种定性与定量分析相结合的系统分析方法，它在经济学领域的应用较为普遍，但对于控制系统而言也可以借鉴这一方法。对于具有大量先验经验的工程师而言，已经对多个目标之间相互比对的重要程度有了主观意见，就可以采用层次分析法客观的确定主观决策的权重大小。

层次分析法的重点就是建立判断矩阵并求解判断矩阵的最大特征根λmax对应的归一化特征向量W，然后对判断矩阵进行一致性检验，如果检验通过，则该特征向量就是各目标的加权系数。下面以一个三性能指标的二阶积分系统为例说明层次分析法在优化控制中的使用方法。

假设如下一个二阶积分系统

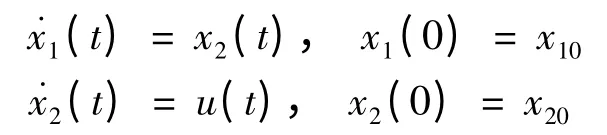
其性能指标为

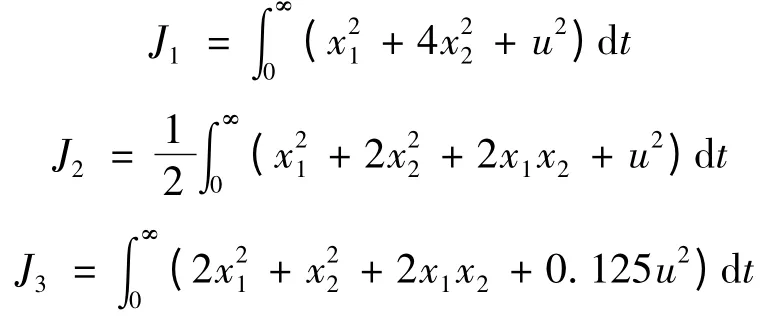
首先根据Saaty 教授提出的标度法(如表1 所示)对各目标相对于其他目标的两两比较重要性来确定判断矩阵B。然后通过和积法(或方根法)求判断矩阵B 的最大特征根λmax，再由式(8)和(9)求出一致性指标CI 和一致性比率CR，检验B 的一致性，最后求λmax的归一化特征向量W。

表1 标度法

采用和积法求取判断矩阵B 的最大特征根λmax及其归一化特征向量W，其步骤如下:

1) 将判断矩阵B 的每一列元素作正规化处理

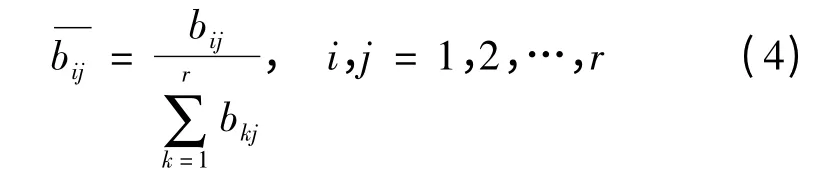
2) 将每一列经正规化后的判断矩阵按行相加

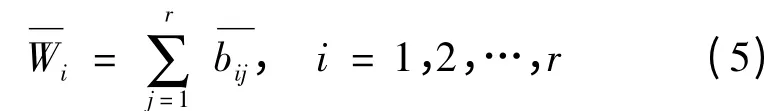
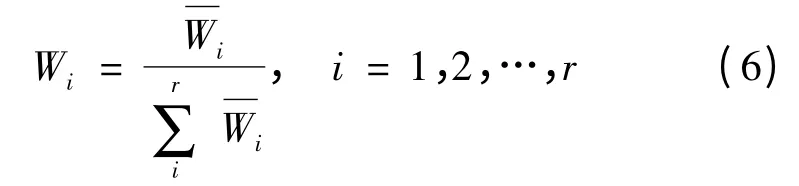
则W = (W1，W2，…，Wr)T即为B 的最大特征根λmax对应的归一化特征向量。

4) 计算判断矩阵B 的最大特征根

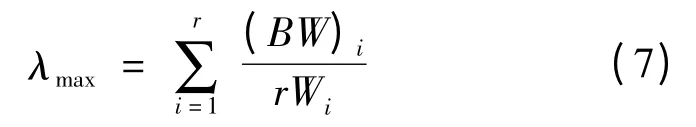
判断矩阵B 的满意一致性可用一致性比率CR检验

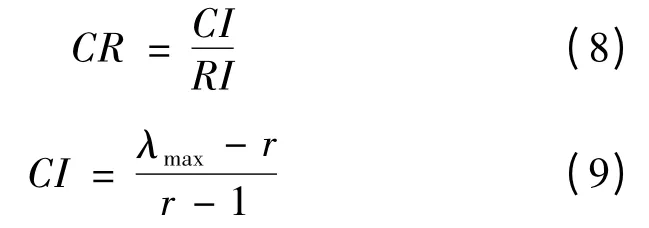
称CI 为判断矩阵B 的一致性指标，CI 越小，B的最大特征根λmax越接近完全一致性判断矩阵的最大特征根。当CR ＜0.1 时，则判断矩阵B 具有满意一致性。否则，判断矩阵B 不具有满意一致性，需要对判断矩阵B 进行调整。

按照上述方法对假设的二阶积分系统的性能指标进行权值计算，首先根据3个指标重要性的两两比较来建立判断矩阵B，如表2 所示。然后用和积法进行计算，可得λmax= 3.009 ，RI = 0.580 ，CI =0.005 ，CR = 0.09 ＜0.1 ，通过一致性检验，得到各目标的权值为W1= 0.540 ，W2= 0.163 ，W3=0.297 。

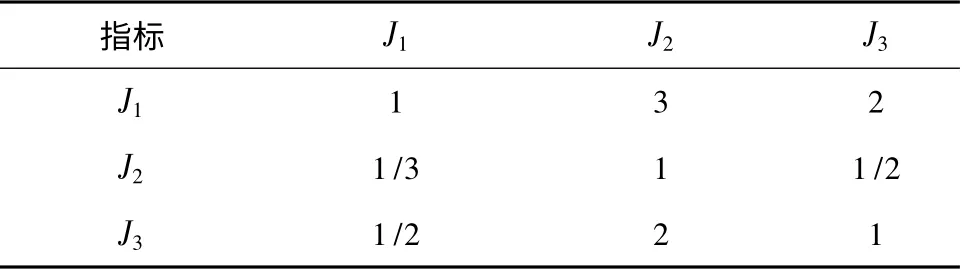
表2 判断矩阵

则该二阶积分系统的性能指标为

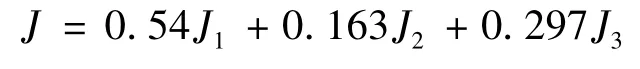
3 交互式决策

在一些工程实际中，工程师对各指标的重要程度不具有先验经验或者各专家关于指标重要程度有分歧，则可通过交互式决策方法供决策者来协调多项指标。

对于多目标优化问题而言，目标解的好坏无法用传统意义上的“好坏”来衡量，这意味着不能采用传统的基于导数信息的优化技术或传统的启发式随机搜索方法(模拟退火、遗传算法、人工免疫算法等)来求解该问题。因此，多目标优化算法的提出是解决此类问题的关键，区别于传统的计算方法，本文采用改进的免疫克隆选择多目标优化算法来求解这类问题。

3.1 多目标优化

多目标优化问题(MOP)可用如下数学表达式描述:

给定决策向量X = (x1，x2，…，xn)∈Ω，它满足下列约束

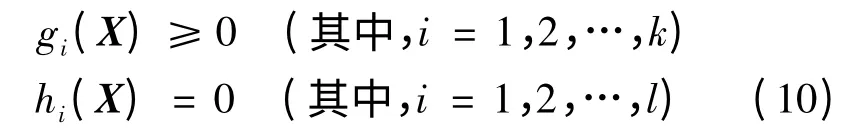
设有r个优化目标，且这r个优化目标是相互矛盾的，一方收益会导致一方利益受损，则优化目标可以表示为

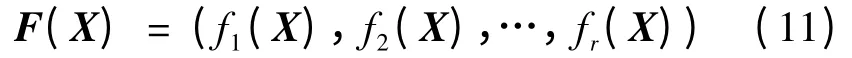
寻求X*= ()使得F(X*)最优，且满足式(10)的2个约束条件。在此基础上给出如下几个重要定义。

定义1 如果X 满足约束条件(10)，则称X 为可行解。所有可行解组成的集合称为可行解集合，记为Ω。

定义2 设X 和X*是多目标优化问题候选解集中的任意2个非等值个体，假定X*是非支配的(Pareto－占优)，则需要满足如下条件:

1)对于所有的子目标，X*不比X 差，即fk(X*)≤fk(X)，(k = 1，2，…，r);

2)至少存在一个子目标，使得X*比X 好，即∃q ∈{1，2，…，r}， 至 少 有 一个 子 目 标 使fq(X*)＜fq(X)。其中，r 为子目标的数量，此时可用“ ＞”表示两者的关系，即X*＞X。

定义3 若X*∈Ω，且不存在其他的使得成立，且其中至少一个是严格不等式，则称X*是minF(X)的Pareto最优解

定义4 Pareto 最优解集在其目标函数空间中的表现形式称为Pareto 边界(或称为Pareto front)，Pareto 最优边界PF*定义为:

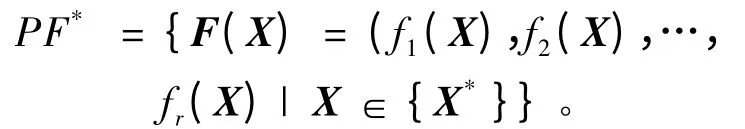
3.2 免疫克隆选择多目标优化算法

免疫是生物体的一种生理机能，生物依靠这种功能识别“自己”和“非己”成分，从而破坏和排斥进入人体的抗原物质，或人体本身所产生的损伤细胞和老化细胞等，以维持人体的健康。本文所用算法主要模仿了脊椎动物的免疫应答及免疫记忆过程。图1 为人体免疫应答过程的一个简化示意图，为更清楚的描述这一过程与算法的对应关系，现给出以下定义。

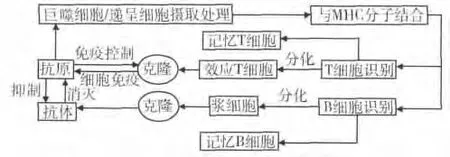
图1 生物免疫应答过程

抗原:抗原(antigen)是指能刺激机体免疫系统引发免疫应答而产生抗体和致敏淋巴细胞，并能与之发送特异性结合而产生免疫效应的物质。在多目标优化问题中，抗原定义为目标函数或目标函数的变换函数。

抗体:抗体是指免疫系统受到抗原刺激后，B 淋巴细胞转化为浆细胞并产生能与抗原发生特异性结合的免疫球蛋白(immunoglobulin，Ig)，该免疫球蛋白即为抗体。在人工免疫系统中一般指问题的候选解，与进化算法中的个体相似，抗体的集合称为抗体群。

设抗体a 代表一个候选解，a = (a1，a2，…，an)，那么一个规模为N 的抗体群定义为:A = {a1，a2，…，aN}。

抗体－抗原的亲和力:抗体和抗原的作用是通过力或化学键实现的，抗体单个结合部位与单价抗原(或表位)的结合力称为亲和力(affinity)。反映整体抗体分子与抗原之间总的结合力称为亲合力(avidity)。在单目标的人工免疫系统一般是指抗原的适应度，在多目标情况下可以是抗体的支配与非支配情况或序值。

抗体－抗体亲和度:抗体与抗体间的结合能力称之为抗体－抗体亲和度。在人工免疫系统中，一般指候选解间的距离。

克隆:克隆是指通过无性生殖而产生遗传上均一的生物群，即具有完全相同的遗传物质组成的一群细胞或者生物个体。在多目标情况下克隆主要实现候选解的复制，克隆比通常取5 ～10。

克隆操作Rcc 定义为:当对第it 代群体A(it)={a1(it)，a2(it)，…，aN(it)}进行克隆操作时，可以表示为:

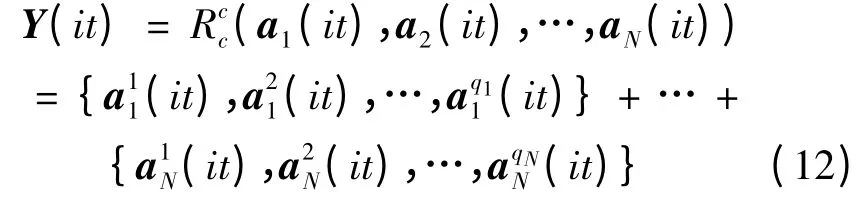
3.2.1 算法编程及测试

(1)编码

对于连续变量而言，二进制编码存在严重缺陷，传统的二进制编码，在处理个体拥挤距离时，通常是采用相似度函数进行判别。但是相似度函数的判别结果有时和实际情况大相径庭。例如1000000000和0111111111 这2个个体，在表现型空间中是相邻的点，具有最小的欧氏距离，但是在基因型空间中却具有很大的Hamming 距离。因此本文采用实数编码。

对于函数优化问题，实数编码最为有效，并且已经证实，在函数优化和约束优化领域，实数编码比二进制和Gray 编码更为有效。实数编码的遗传算子大体上有4 类:传统算子、算数算子、基于方向的算子和随机算子。本文采用传统算子。

(2)进化算子

高斯变异(Gaussian Mutation)是改进算法对重点搜索区域大局部搜索性能的另一种变异操作方法。所谓高斯变异操作是指进行变异操作时，用符合均值为m，方差为δ2的正太分布的一个随机数来替换原有基因值。高斯变异的具体操作过程是:

1)每个染色体上都进行变异操作，变异的基因位选择方式为

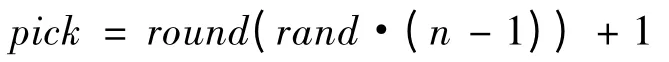
2)对每一个变异点，以概率pm 从对应基因的取值范围内取一随机数来取代原有基因值。新基因由下式计算得到:

设xk为变异点，其取值范围是，则令

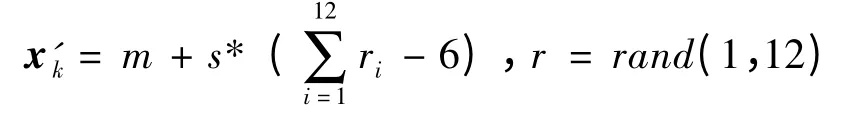
当问题的抗体约束范围较广时，高斯变异方法所得的Pareto 最优解分布的均匀性会变差。因此，在这种情况可以使用均匀变异算子。均匀变异是用抗体约束范围内均匀分布的随机数来取代变异基因位，其MATLAB 程序表述为如下:

算法中，chrom 表示需要进行变异操作的抗体，pm 为变异概率，bound 为变异基因位的取值范围，通常以矩阵形式描述。

3)选择算子

克隆选择操作是从抗体各自克隆增殖后的子代中选择优秀的个体，从而形成新的抗体群。一个抗体能否被选择到下一代中，主要取决于其是否为非支配抗体。这样就需要将抗体群划分为支配抗体群和非支配抗体群，这也是算法的主要时间复杂度所在。本文采用擂台法进行非支配操作，其时间复杂度为O(rmN)。

擂台法构造进化群体的Pareto 最优解集时，每一轮从构造集中选一个解作为擂台主，其余个体依次打擂台，失败者则被淘汰出局，胜者成为新的擂台主，并继续该轮比较。一轮比较后，最后的擂台主即为非支配个体。按这种方法进行下一轮的比较，直到构造集中的被支配个体都被淘汰出局。算法的时间复杂度为O(rmN)，式中r 为目标数，m 为非支配个体数，N 为群体大小，比起NSGA－II 算法的复杂度(O(rN2))有所降低。

4)种群修剪

为保持种群良好的分布性和均匀性，需要对种群进行修剪。其重要思想是:计算抗体之间的聚集距离，并以此分配适应值，两端个体分配无穷大适应值，以此来选取非支配且聚集距离大的个体产生新的种群。这样还能保证抗体规模维持在设定范围内，而不至于过渡繁殖。

5)依概率免疫记忆

对抗原进行进化操作时，按概率保留一定的非支配抗原作为精英，以此为算法必然收敛的前提。为验证算法的性能，选取了kur，MOP5 和MOP7 三个标准测试函数。图2 为免疫克隆选择多目标优化算法的算法流程图。图3(a)～(c)分别为免疫克隆选择多目标优化算法的kur，MOP5 和MOP7 函数测试结果。图3(d)为NSGA－II 算法的MOP5 测试结果。相比而言，由于算法省去了二进制到十进制的转换及交叉等操作，比起NSGA －II 的执行时间更短。由图3(c)和(d)比较可见针对3个目标的测试结果，免疫克隆选择多目标优化算法的Pareto 最优解分布更广泛，要优于NSGA－II。

3.3 基于Pareto 最优的多目标系统最优控制方法

用交互式决策方法来求解多目标系统最优控制问题需要将算法与模型仿真相结合。在Matlab 环境下建立算法的M 文件，并通过语句assignin(ws，‘var’，val)和［t，x，y］= sim(model，timespan)建立多目标免疫优化算法与需求解问题的Simulink 仿真模型之间的联系。为说明交互式决策法及免疫克隆选择多目标优化算法在求解实际问题时的有效性，本文以飞机增稳控制器的设计为例进行说明。

3.3.1 示例

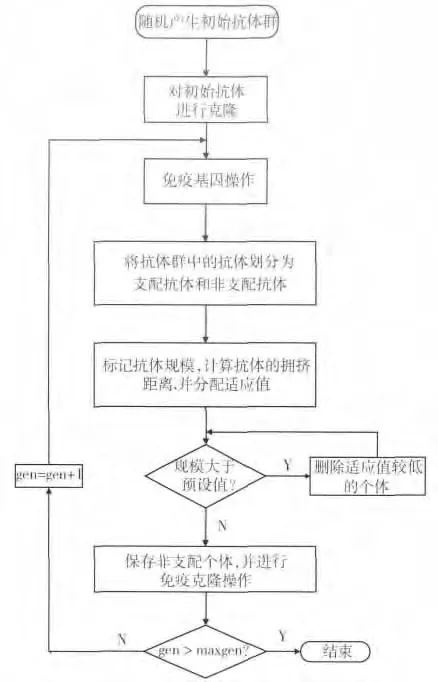
图2 免疫克隆选择多目标优化算法流程

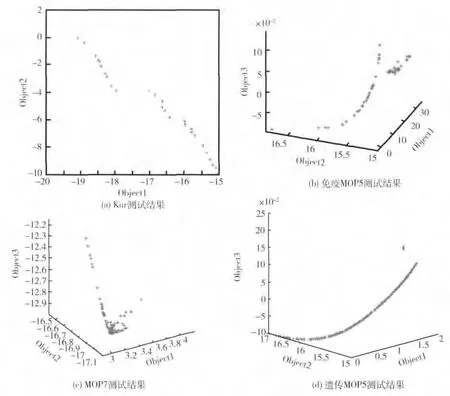
图3 算法测试结果

高性能飞机的飞行包线范围很广，要满足高空高速，低空低速的要求，且在受到自然环境影响(如自然风)下仍能保证较好的稳定度，仅依靠飞机的气动外形设计很难实现，因此需要在飞机中加入增稳系统，以提高飞机的稳定性和操纵性。这类为增加和改善飞机稳定性的控制系统称为增稳系统(Stability Augmentation Systems，简称SAS)。由于本文只为说明免疫算法对多目标系统的优化控制方法，故对SAS 这一多输入多输出系统做以下简化:1)飞机模型采用纵向小扰动线性化模型，其线性化平衡点处于飞行包线内低空高速区域;2)将问题简化为状态调节器，不考虑指令输入;3)仅考虑垂直风干扰，迎角的初始条件为5°的偏转。使用王青在文献［4］中提供的数据，建立以下状态空间模型

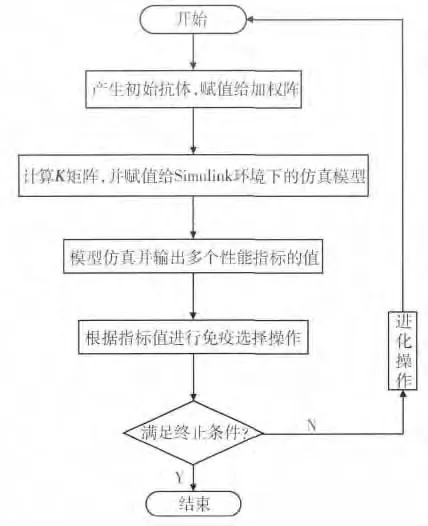
图4 免疫克隆选择多目标优化算法求解LQR 控制器

式中，状态向量x = ［υ，α，q，θ］T，各元素分别代表速度的变化百分比、迎角、俯仰角速率、俯仰角;u =［ξp，ξT］T，各元素分别代表升降舵的偏转和油门杆的位置。LQR 全状态反馈最优调节器的性能指标选取如下:

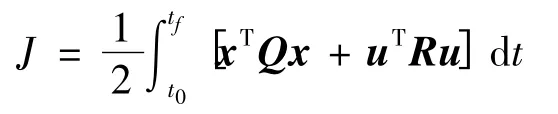
对于该问题的性能给出3个指标，分别为:升降舵控制输入的最大值max(u)、迎角输出的峰值时间tp和超调量σ 以及估计误差的ITAE。如图4 所示，为免疫克隆选择算法结合多指标飞机增稳LQR控制器设计的流程图。算法得到的抗原经计算得到LQR 的反馈阵参数并赋给Simulink 环境下的控制器。用模型进行仿真，将仿真后得到的性能指标参数又返回给多目标免疫算法，算法根据这一数值进行免疫操作。整个计算过程以此循环，直到算法满足终止条件。

图5 为3个性能指标的Pareto 最优边界。表3为从非支配集中任意选出的5 组抗体得到的控制器参数。图7 为系统的Simulink 仿真模型。图6 为从表3 中选取的第1 组控制参数和第5 组参数进行仿真所获得的迎角输出曲线，由曲线可知，同样获得飞机增稳控制的同时，系统的性能指标的极小值取值有所不同，如图6(a)对应的控制器系统稳定性及稳定时间均劣于图6(b)对应的控制器，但是图6(a)对应的控制器所消耗的控制能量却小于后者。因此，决策者可根据计算所得的控制器参数来协调多项系统指标以达到最优控制。

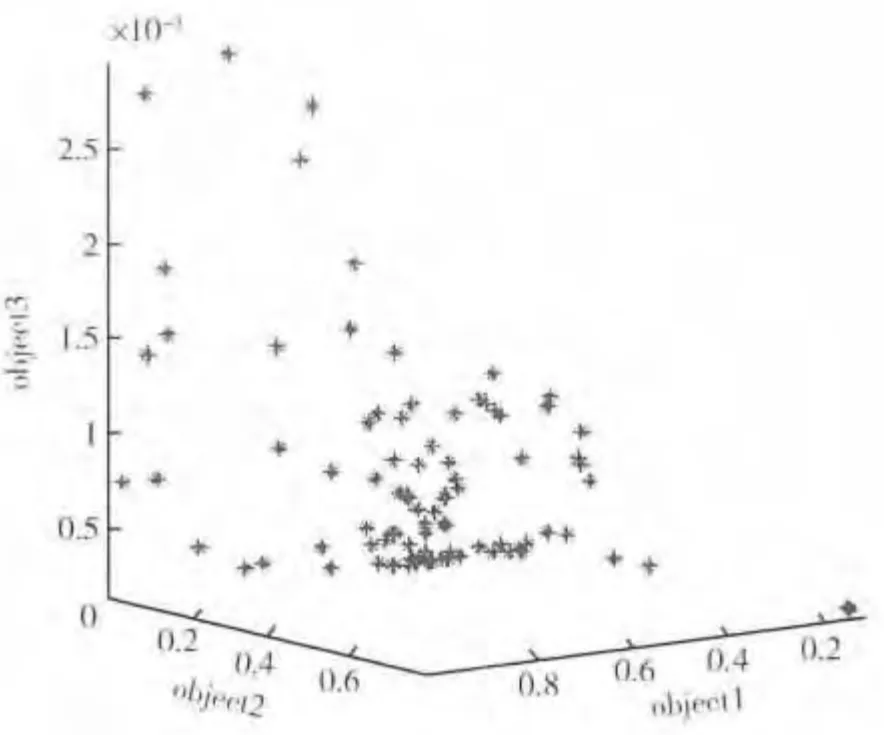
图5 Parcto最优边界

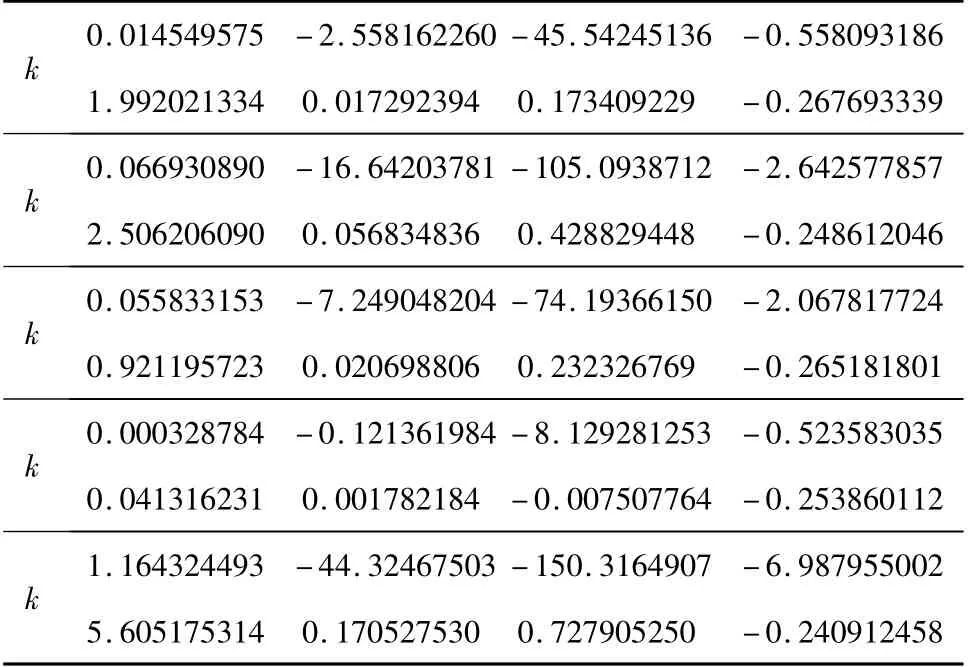
表3 控制器可选参数

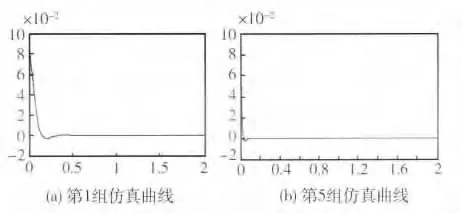
图6 系统迎角仿真曲线

4 结论

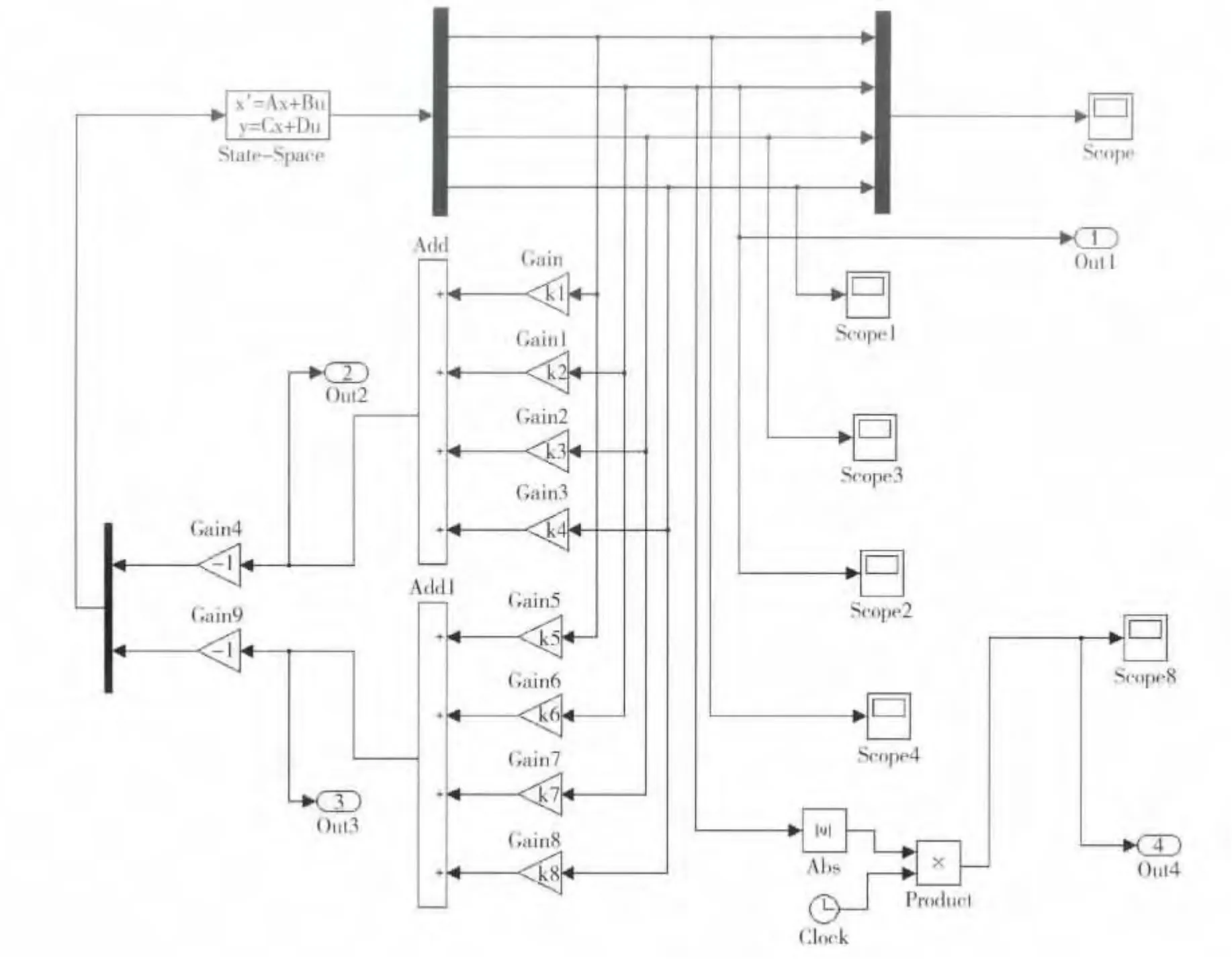
图7 增稳系统的Simulink 仿真模型

对多目标系统的最优控制方法进行了深入研究，并根据设计者先验知识的多少提出了2 种新的解决方法:层次分析法和交互式决策法。不同于以往解决方法，交互式决策法的数值计算难度小，且不依赖或很少依赖求解问题。不论是线性或非线性、连续或非连续问题均能够求解其最优控制参数，还能兼顾多项性能指标。在所采用的算法方面，本文针对现有算法的不足，设计了免疫克隆选择多目标优化算法来求解多目标问题，通过测试表明算法性能良好，能够用于多目标系统最优控制参数的求解。本文所提方法不仅可以应用在多指标情况下的LQR 设计，还可以应用在多指标要求下的油田最优采收率、炼油过程中的换热和加催化等的控制以及直升机悬停控制等诸多方面。

［1］Khargonekar P P，Rotea M A. Multiple Objective Optimal Control of Linear System:The Quadratic Norm Case［J］. IEEE Trans. Automatic Control，1991，36(1):14-24.

［2］Salukvadze M E. Vector-valued Optimization Problem in Control Theory［M］. Academic，New York，1979.

［3］张成科.多目标最优控制的小波逼近解［J］. 数学的实践与认知，2006，36(8):176-183.(Zhang C K.Ap proximation Solution for Multiple Criteria Optimum Control Problem Via Wavelet［J］. Mathematics in Practice and Theory，2006，36(8):176-183.)

［4］王青，陈宇，张颖昕，侯砚泽. 最优控制—理论、方法与应用［M］.北京:高等教育出版社，2011.(Wang Q，Chen Y，Zhang Y X，Hou Y Z. Optimal Control—Theory，Methods and Applications［M］.Beijing:Higher Education Press，2011.)

［5］Shtessel Y B. Principle of Proportional Damages in a Multiple Criteria LQR Problem［J］. IEEE Trans. Automatic Control，1996，41(3):461-464.

［6］Holland J H. Adaptation in Natural And Artificial Systems:An Introductory Analysis With Applications to Biology，Control，and Artificial Intelligence［M］. 1st Edition，Ann Arbor，MI:The University of Michigan Press，1975;2nd edition，Cambridge，MA:MIT Press，1992.

［7］Schaffer J D. Multiple Objective Optimization With Vector Evaluated Genetic Algorithms［C］. Proceedings of 1st International Conference on Genetic Algorithms and Their Applications. Hillsdale:Lawrence Erlbaum Associates，Inc.，1985:93-100.

［8］Deb K，Pratab A，Agarwal S，et al. A fast and Elitist Multi-objective Genetic Algorithm:NSGA-II［J］. IEEE Transactions on Evolutionary Computation，2002，6(2):182-197.

［9］Coello Coello C A，Cruz Cortés N. An Approach to Solve Multiobjective Optimization Problems Based on An Artificial Immune System［C］. Proceedings of 1st International Conference on Artificial Immune System，Canterbury，2002:212-221.

［10］郑金华.多目标进化算法及其应用［M］. 北京:科学出版社，2007.(Zheng J H. Multi－objective Evolutionary Algorithm and Application ［M］. Beijing:Science Press，2007.)

［11］Jiao L C，Gong M G，Shang R H，et al. Clonal Selection with Immune Dominance and Anergy Based Multiobjective Optimization［C］. Proceedings of 3rd International Conference on Evolutionary Multi-crite-rion Optimization，Berlin:Springer，2005:474-489.

［12］焦李成，尚荣华，马文萍，公茂果，李阳刚，刘芳.多目标优化免疫算法、理论和应用［M］. 北京:科学出版社，2010. (Jiao Licheng，Shang Ronghua，Ma Wenping，Gong Maoguo，Li Yanggang，Liu Fang. The Theory and Application of Multi-objective Optimization Immune Algorithm［M］.Beijing:Science Press，2010.)

［13］Knowles J D，Corne D W，Deb K.Multiobjective Problem Solving form Nature［M］.New York:Springer，2008.

［14］Gong T，Cai Z X. Natural Computation of Immune Elearning System［C］//Proc. of 3rd Int’1 Conf. on Computational Intelligence，Robotics and Autonomous Systems，Singapore，2005:13-16.