基于单边攻角特性的吸气式飞行器下压制导律设计与仿真

梁 卓 雷延花 韩英宏 严佳民 廖选平

中国运载火箭技术研究院，北京100076

对于一类只有单边攻角特性的吸气式飞行器:一方面，由于进气道设计的限制，为保证飞行器在整个飞行过程中发动机正常工作，需确保发动机攻角极性保持不变，同时将侧滑角稳定在0°附近，需采用BTT 制导模式［1－3］;另一方面，飞行器飞行过程中不可避免地存在拉起和下压2 种形态，相应地存在正攻角和负攻角2 种模态。为确保只具有单边攻角特性的飞行器实现拉起和下压，需采用BTT－180制导模式，在下压时进行180°滚转，利用正攻角进行下压［4］。为保证下压段滚动过程的平稳性，需对滚动时间进行优化，因此，本文在飞行器滚动过程中引入模糊控制，根据起控点的滚动角和滚动角速度优化滚动时间，提高滚动过程的平稳性，为实现对目标的精确打击创造有利条件。

1 下压段制导律设计

飞行器与目标几何关系在纵向平面内的投影如图1 所示。

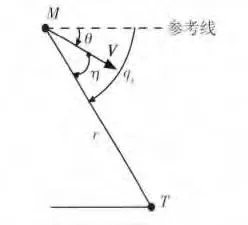
图1 弹目几何关系图

其中，M 为飞行器;T 为目标;r 为飞行器与目标相对距离;V 为飞行速度;qy为目标视线高低角(约定由参考线逆时针旋转至弹目连线为正);η 为速度矢量前置角(约定由速度方向逆时针旋转至弹目连线为正(负));θ 为弹道倾角。

几何关系可描述为

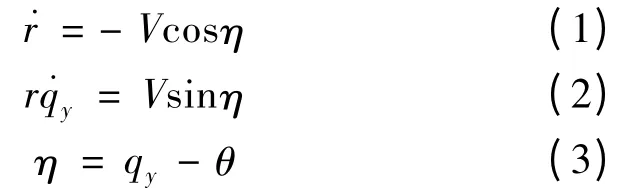
对式(2)微分，有

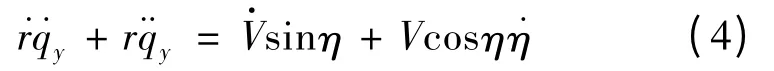
将式(1)～(3)代入式(4)，有

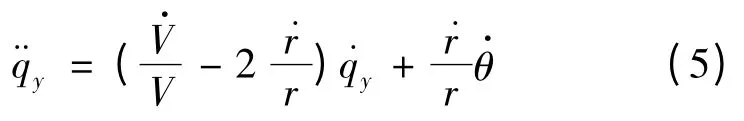
对式(5)建立线性最优二次型目标函数，并进行逆Riccati 积分得到

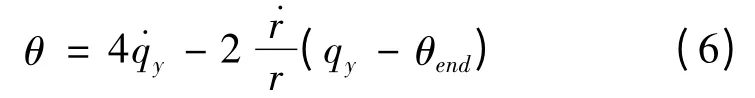
纵向指令过载

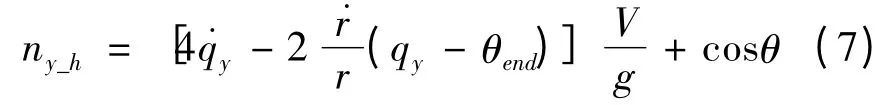
同理可得侧向指令过载

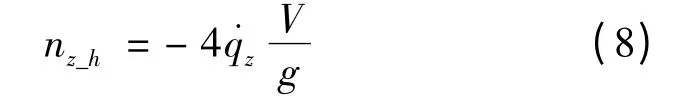
2 BTT－180 制导律设计

由最优比例导引律解算得到弹道坐标系下的纵向过载ny_h和侧向过载nz_h，计算总攻角α 和速度倾斜角ν。在此基础上，根据弹体坐标系(B)、速度坐标系(V)与发射坐标系(G)之间的转换关系计算俯仰角ϑ、偏航角ψ 和滚动角γ。

2.1 总攻角指令和速度倾斜角计算

(1)总攻角

纵向和侧向合成指令过载为

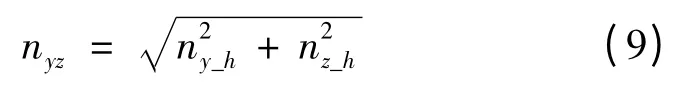
对应的总攻角指令

(2)速度倾斜角解算

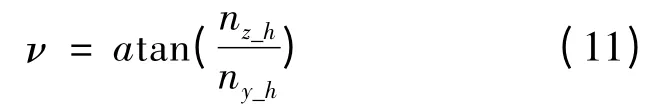
2.2 滚动角指令、俯仰角、偏航角解算

(1)滚动角指令

弹体坐标系(B)、速度坐标系(V)与发射坐标系(G)之间的转换关系为BG = BV·VG。

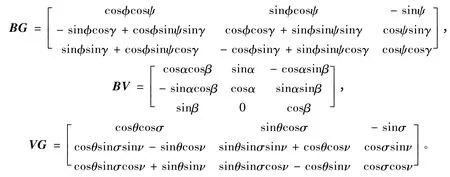
式中，－ sinψ = cosαcosβ(－ sinσ)+ sinαcosσsinν + (－ cosαsinβ)cosσcosν。

由此得到，

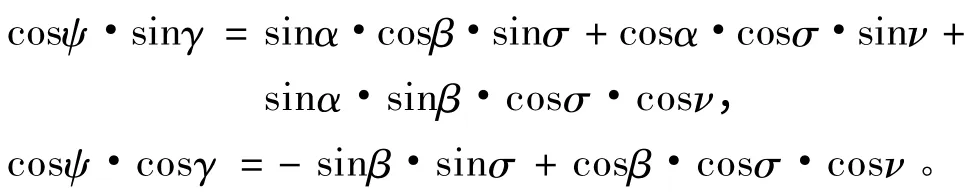
则滚动角指令计算方法如下

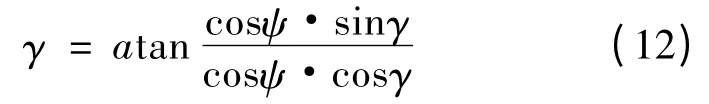
由此得到BTT 制导指令为

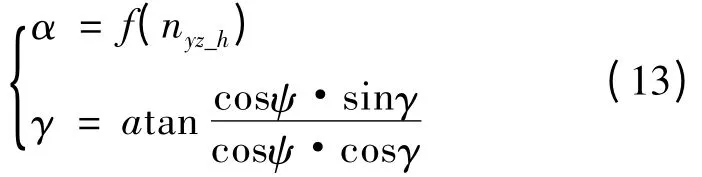
(2)俯仰角计算

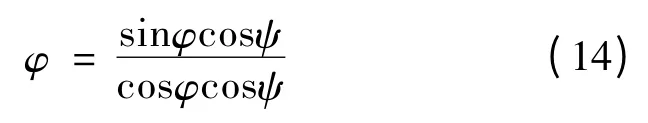
式中，

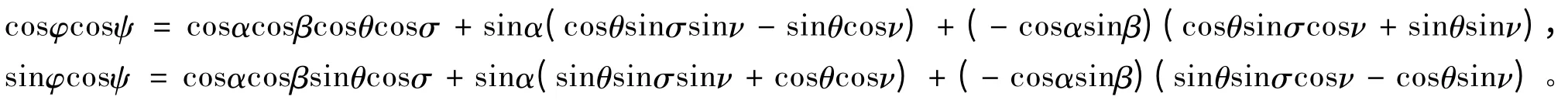
(3)偏航角计算

式中，

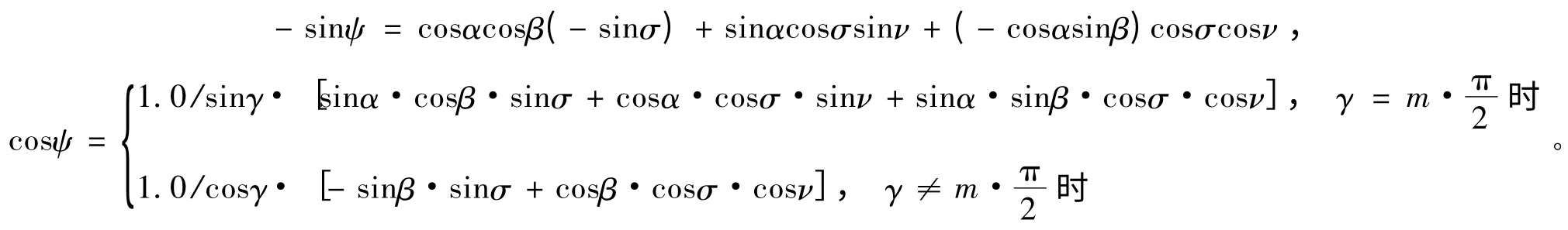
2.3 基于模糊逻辑的滚动控制律优化

下压时，为确保发动机单边正攻角特性，进行180°弹体滚动，利用正攻角实现下压。滚控方程描述如下:

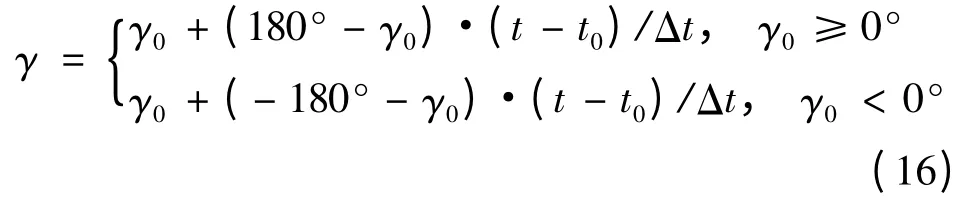
在滚动过程中，为确保下压段滚动过程的平稳性，在飞行器滚动过程中引入模糊控制器，根据下压开始时刻(即180°滚动起控时刻)滚动角γ0和滚动角速度优化滚动时间Δt，t0表示起控时刻。

考虑到所设计的控制器需要满足飞行控制的实时性要求，故采用离线计算、在线查表的模糊控制方法。即可以针对输入情况的不同组合离线计算出相应的控制量，从而组成一张控制表，实际控制时只需查表即可，避免了大量的在线计算。

NB:负大;NM:负中;NS:负小;ZR:零;PS:正小;PM:正中;PM:正大。

输入变量和输出变量的论域为［－3，3］，模糊推理规则运用肯定式:

Ri:若σ 是Ai且˙σ 是Bi，则ufuzzy是ci。其中Ai，Bi是模糊子集，ci为第i 条模糊控制规则。由此得出表1 所示的模糊控制规则表。

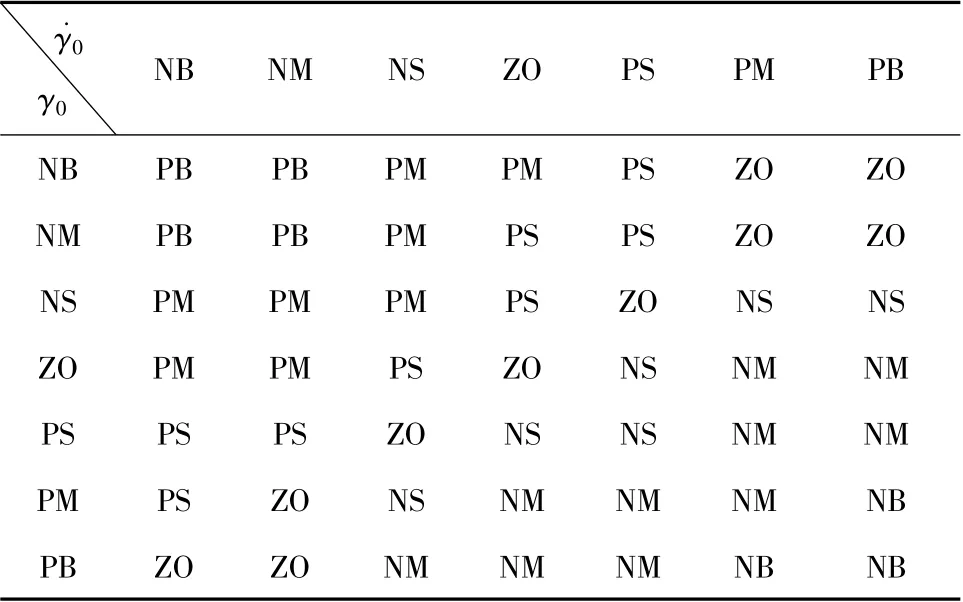
表1 模糊控制规则表

模糊化方法采用重心法，模糊控制器输出变量为

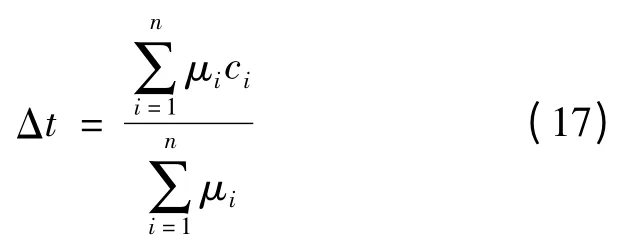
其中，μi为第i 条模糊规则的隶属度，n = 49 ，为模糊控制规则总数。

3 仿真算例与分析

为考核下压段BTT －180 制导律的有效性，并验证基于模糊逻辑的滚控正确性，需考虑180°滚动起控时滚动角取不同值状态下的仿真工况。因此，综合以上要求，分别进行横向不机动和横向机动10km 这2 种工况下压段飞行轨迹仿真。在不考虑偏差和干扰条件下，横向不机动时，起控时滚动角为0;横向机动时，起控时滚动角不为0。

横向不机动和横向机动10km 这2 种状态下180°滚动开始时的滚动角初值和滚控时间见表2，主要仿真结果如图2 ～5 所示。

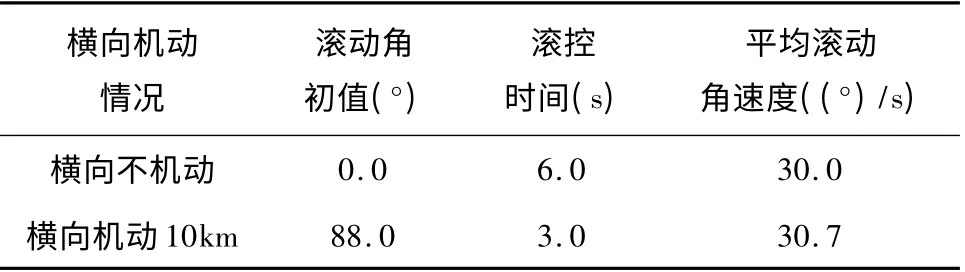
表2 滚动角初始值和滚控时间

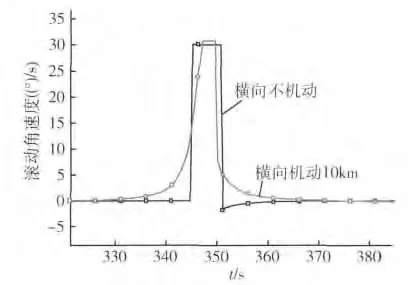
图2 滚动角速度－时间曲线

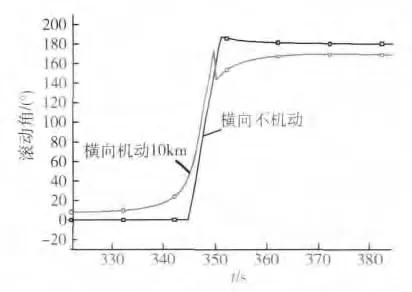
图3 滚动角－时间曲线

由以上仿真结果可以看出:

1)下压段采用正攻角实现了下压，表明BTT－180制导律数学模型的正确性;

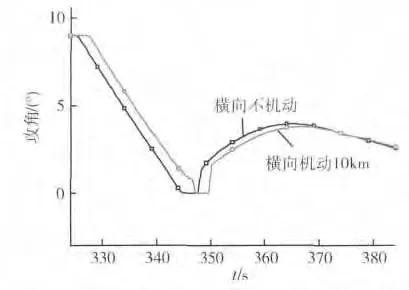
图4 攻角－时间曲线

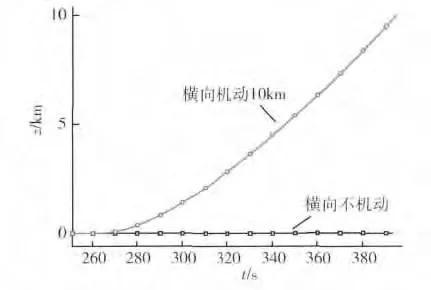
图5 横向位置－时间曲线

2)以开始180°滚动时的初始滚动角和初始滚动角速度为观测量，基于模糊控制方法在线调整滚控时间，可实现滚控过程的平稳性。

4 结论

以一类只有单边攻角特性的吸气式飞行器为研究对象，提出了一种基于模糊控制的下压段BTT －180 制导律设计方法，采用模糊控制完成了下压飞行段飞行器180°的平稳滚动，利用正攻角实现了飞行轨迹下压。最后以2 种典型工况为例，进行了数学仿真，仿真结果说明了该方法的合理性与有效性。同时该方法算法简单，自适应性强，因此具有一定的工程应用前景。

［1］段磊.一种针对采用冲压发动机的远程空空导弹末段制导算法研究［J］. 科学技术与工程，2012，12(27):7013-7018. (Duan Lei. Research on Terminal Guidance Algorithm for Ramjet-powered Airborne Missiles［J］.Science Technology and Engineering，2012，12(27):7013-7018.)

［2］Asif Farooq，David J N Limebeer. Bank-to-Turn Missile Guidance with Radar Imaging Constraints［J］. Journal of Guidance，Control，and Dynamics，2005，28(6):1157-1170.

［3］田国兵.带落角约束的BTT 飞行器制导控制一体化方法研究［D］.哈尔滨工业大学，2011. (Tian Guobin.Integrated Guidance and Control for BTT Missile with Terminal Impact Angle Constraint［D］. Harbin Institute of Technology，2011.)

［4］叶振信，李传峰，傅维贤.大气层内无动力滑翔炸弹倾斜转弯控制设计［J］. 导弹与航天运载技术，2010(6):6-9.(Ye Zhenxin，Li Chuanfeng，Fu Weixian.Bankto-Turn Control Design for No －power Gliding Bomb inside Atmosphere［J］. Missiles and Space Vehicles，2010(6):6-9.)

［5］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2000. (Qian Xingfang，Lin Ruixiong，Zhao Yanan. Missile Flight Dynamics［M］.Beijing:Publishing Company of Beijing Institute of Technology，2000.)

［6］赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997. (Zhao Hanyuan. Vehicle Reentry Dynamic Properties and Guidance［M］. Changsha:Publishing Company of National University of Defense，1997.)