运载火箭复杂容错控制系统可靠性分析

胡海峰

北京航天自动控制研究所，北京100854

飞行控制系统(简称控制系统)是运载火箭的关键系统，系统复杂、投入大、风险高，特别是载人飞行，关系到宇航员的生命安全，因此对运载火箭控制系统提出了高可靠性要求［1］。冗余容错设计是提高系统可靠性和安全性的重要手段，普遍应用于运载火箭控制系统，通过投入超过常规设计所需的外加资源来抵消故障产生的后果，在提高系统可靠性的同时，必然增加其复杂性。系统采用冗余设计并具备容错功能时，将存在着多级多重表决或贮备，复杂度大大增加，往往不能用简单的数学模型来描述，建立系统可靠性模型变得异常困难。

本文在典型可靠性分析模型及理论基础上，研究运载火箭复杂容错控制系统可靠性模型建模方法，并对2 种典型冗余容错系统进行算例分析。

1 典型系统可靠性模型

复杂系统的可靠性模型往往是由若干典型结构的可靠性模型组合而成，典型系统可靠性模型有串联、并联、串并联、并串联、表决和储备等，本节主要给出串并联、并串联、表决、储备系统的可靠性模型。

1.1 串并联系统

由串联系统和并联系统组成的先串联再并联的混合冗余系统称为串并联系统，常用的2 种串并联系统如图1 所示。

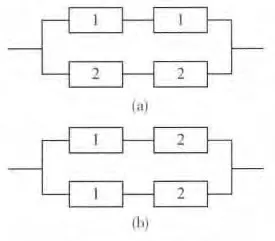
图1 串并联系统

图1(a)和(b)两种系统在各单元可靠性相同的情况下，整个系统的可靠性是相同的，其可靠性计算数学模型为:

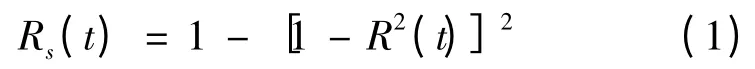
图1(a)和(b)两种系统的区别是:1)系统每条支路由一个控制器控制;2)系统每条支路由2个控制器控制。

1.2 并串联系统

由串联系统和并联系统组成的先并联再串联的混合冗余系统称为并串联系统，常用的2 种并串联系统如图2 所示。(a)和(b)两种系统在各单元可靠性相同的情况下，整个系统的可靠性是相同的，其可靠性计算的数学模型为:

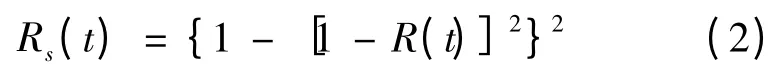
图2(a)和(b)两种系统的区别是:1)系统中的并联部分由2个控制器控制;2)系统中并联部分由1个控制器控制。

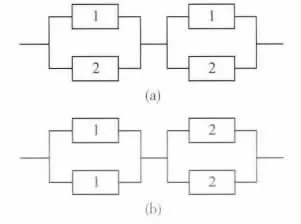
图2 并串联系统

1.3 表决系统

系统由n个单元组成，若其中有k个或k个以上单元正常，则整个系统正常，这样的系统称n 中取k 表决系统，记作K/n(G)。若表决器可靠性为RG，每个单元可靠性相等均为R，则n 取k 多数表决系统的可靠性模型可用二项分布来描述:

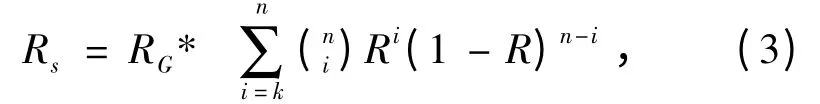
在运载火箭设计中，常用3 取2 模型，示意图如图3 所示。

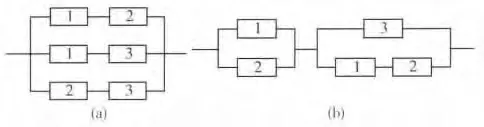
图3 3 取2 系统

图3(a)和(b)是最常见的3 取2 模式，整个系统既可以防一度误判，又可以在一个控制器失效的情况下不影响系统功能，同时通过并联提高了系统的可靠性。在各个单元可靠性相同的情况下，其可靠性计算的数学模型为:

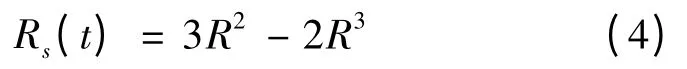
1.4 储备系统

在若干个单元组成的系统中，当主工作单元失效时，储备单元能立刻接替完成主工作单元的功能，这样的系统称为储备系统。储备系统按储备单元在储备期间的失效情况可分为3 类:1)冷储备(无载储备)，储备单元在储备期间失效率为0;2)热储备(满载储备)，储备单元在储备期间失效率与工作单元失效率一样;3)温储备(轻载储备)，储备单元在储备期间失效率大于0 而小于工作单元失效率［2－3］。此处仅给出冷储备系统的可靠性模型，储备单元在储备期间失效率为0。

若各单元寿命均为指数分布，且各单元失效率均为λ，转接开关可靠性为Rsw，则冷储备系统可靠性和平均寿命为:

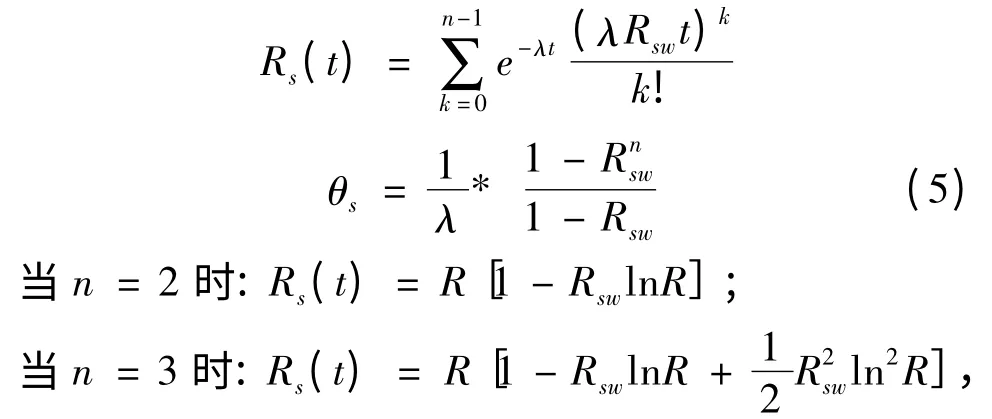
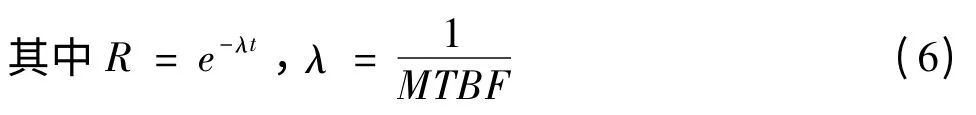
2 复杂容错控制系统可靠性建模

运载火箭控制系统采取冗余设计，且冗余单元之间增加交互表决的通道，基于软件增加故障检测、故障诊断、软件表决、故障吸收和系统重构等功能时，控制系统成为存在多级多重表决的冗余容错系统，需借助复杂容错系统可靠性建模方法建立可靠性计算模型。通常应用的方法主要包括:状态枚举法、全概率分解法、最小路径法、全概率公式法、Petri 网模型等［2－5］。文献［6］给出了基于全概率公式的应用方法;文献［7］提出了基于状态空间法的特高压直流输电系统可靠性评估算法;文献［8］基于K/n(G)模型建立了柔性直流输电系统中换流阀的可靠性模型，并分析了不同设备冗余情况下可靠性指标;文献［9］基于马尔科夫过程建立了柔性直流输电变压器系统的可靠性模型，并对不同设计结构和备用水平变压器系统的可靠性指标进行了对比;文献［10］在FD 法和模型组合的基础上对整个柔性直流输电系统进行了可靠性评估;文献［11］基于状态空间法与K/n(G)模型给出了柔性直流输电系统可靠性模型。但上述方法难以直接应用于运载火箭复杂容错控制系统，本节将以运载火箭的两类典型复杂容错控制系统为例，建立系统可靠性计算模型。为便于分析，系统组成考虑箭机、惯组(IMU)、综合控制器、总线等4 类设备，并且将各单元可靠性统一为R。

2.1 复杂容错系统1 可靠性建模

某典型冗余容错系统，见图4。全箭通过1553B总线网络连接3 套完整的电气系统，形成相对独立的系统级三冗余。设备均为三冗余，每一套由1 条双通道1553B 总线连接，其中箭机和综合控制器均为3 台单机冗余在1个设备中，3 台单机之间通过机内总线进行通讯。控制系统工作时，3个BC(Bus controller，即总线控制器)分别独立录取3 套惯组的数据，获取箭体的角速度、视加速度等信息，之后与其它BC 进行数据交换，使每个BC 都能获得3 套数据;然后3个BC 分别进行方程计算，将控制指令通过总线分别送至3 台综合控制器;综合控制器的3台单机也可以进行信息交互。对于惯组和BC，若3个模块均正常工作，则系统以三模冗余方式工作，采用3 取2 表决机制;若其中1个模块失效，则系统通过故障检测定位将其切除，系统降级为双冗余系统;若又有1个模块失效并被定位切除，则系统以单机模式运行。对于综合控制器，其输出通过硬件实现3 取2 表决，因此若3个模块均正常工作或其中1个模块失效，系统可通过表决屏蔽1个故障模块;若有2个及以上模块失效，系统即失效。因此系统形成计算冗余表决、控制器指令解析冗余表决、输出级功率放大冗余表决同步、总线网络冗余的复杂冗余容错系统结构。

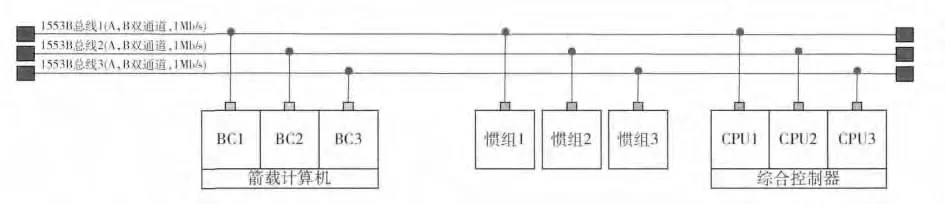
图4 复杂容错系统1

在分析图4 系统可靠性时，虽然每套1553B 总线均有A，B 双通道，当A 总线出故障时可以切换为B 通道，但是考虑到A，B 均故障、总线协议芯片故障以及切换失败的情况，应考虑总线本身的可靠性，这相当于在系统中串联1个单元，框图如图5。

上述系统可直接给出计算公式为:

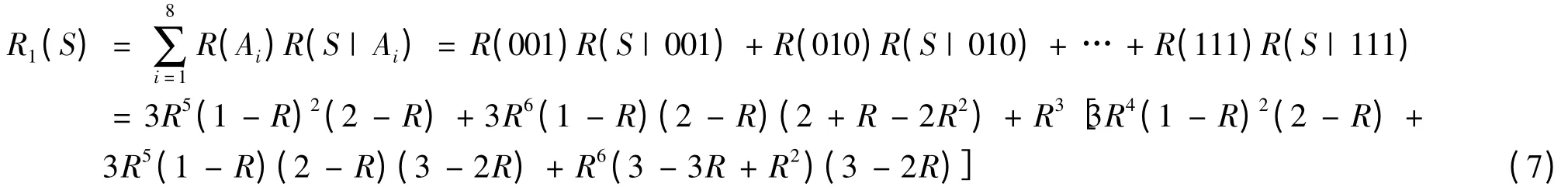
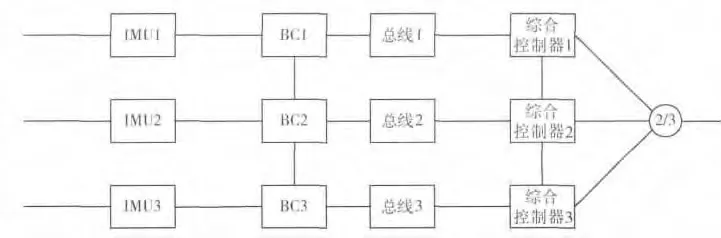
图5 复杂容错系统1 框图

2.2 复杂容错系统2 可靠性建模

某典型冗余容错系统，见图6，与图4 不同之处在于整个系统采用1 套1553B 总线进行连接。在此系统中，3个BC 采用主备方式运行，3个惯组和综合控制器的3 台单机分别作为3个站点挂在总线上，框图见图7。

图6 复杂容错系统2

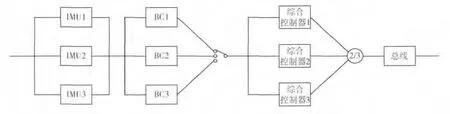
图7 复杂容错系统2 框图

令图6 系统中惯组可靠性为RIMU，BC 可靠性为RBC，综合控制器可靠性为R综控器，总线可靠性为R总线，根据串联系统模型［2－5］，可得系统可靠性:

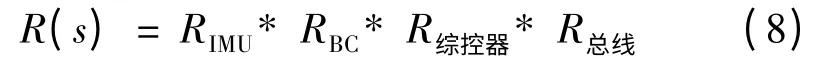
下面分别计算RIMU，RBC，R综控器和R总线。

(1)RIMU计算

系统中有3个IMU，IMU 独立工作，系统冗余录取3个IMU 数据，具备容错功能，能根据零值故障、极值故障、一致性故障等冗余管理算法诊断IMU 信息，控制系统进行信息融合表决，并能基于箭体飞行数据特点、GPS 测量信息综合诊断IMU 数据，RIMU可按n =3 的并联系统模型计算，根据并联系统模型［2－5］，可得:

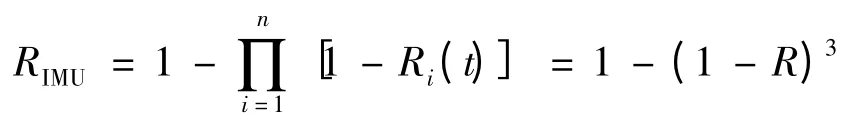
(2)RBC计算

系统中有3个BC，BC 中运行飞行控制软件，完成数据综合、信息容错、冗余管理和控制方程计算等功能，考虑到运载火箭实时控制的需求，运载火箭一般采取跟随、热备的模式，当主工作单元故障时切换到备份单元，备份单元再出现故障时切换到第2个备份单元。飞行过程中跟随、热备的备份单元不参与输出，可视为无载储备。运载火箭飞行时间短，为便于计算，无载储备单元在储备期间可简单地认为失效率为0。基于上述分析，RBC可按n =3 的冷储备模型计算。假设切换可靠性为Rsw，根据式(6)可得:

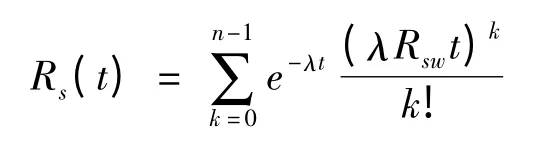
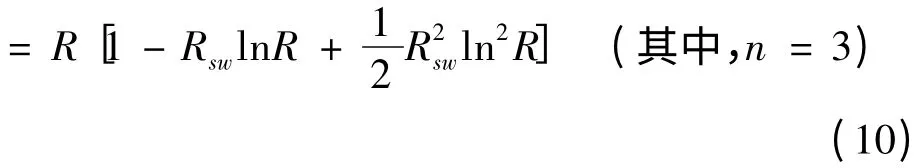
(3)R综控器计算

系统中有3 台综合控制器，3 台综合控制器集成在1个机箱中，3 取2 表决后输出控制信号，因此系统中综控器为3 取2 表决系统，根据式(4)可得:

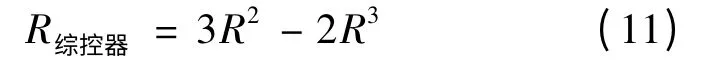
(4)R总线计算

将式(9)～(12)代入式(8)，可得系统可靠性:

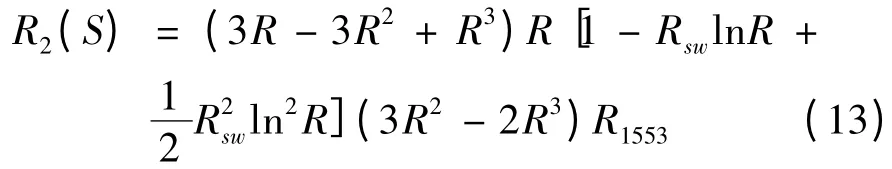
3 算例计算与分析

3.1 可靠性计算

运载火箭控制系统单元模块或单机可靠性R一般不低于0.990，令R在0.990 ～0.9999 变化，R1553在0.99 ～1 变化，Rsw= 1，分别代入式(7)和(13)，按控制系统可靠性模型计算R1(S)，R2(S)，主要计算结果见表1，在上述条件下系统可靠性随单机可靠性变化见图8。

为保证可靠性，航天运载器普遍采用高等级元器件，单元模块或单机可靠性一般比较高，选择单元模块或单机可靠性R =0.999，令Rsw在0.999 ～1 变化，R1553在0.99 ～1 变化，分别代入式(7)和(13)，按控制系统可靠性模型计算R1(S)，R2(S)，主要计算结果见表2，在上述条件下系统可靠性随Rsw可靠性变化见图9。

3.2 讨论与分析

由于BC 的核心控制作用，其故障容易导致R1其它终端的资源浪费，影响系统可靠性，但由于R1总线并联容错，使它对总线本身故障的敏感度大大降低;R2 系统中只要BC 切换正常(Rsw=1)，单个BC 故障就不会蔓延到终端及系统，但由于总线是串联环节，因此R2 对总线本身的故障比较敏感。根据表1 和图8 结果，Rsw=1 时，1553B 总线可靠性指标较低时，R1 的系统可靠性大于R2;1553B 总线可靠性达到0.99999 ～1 时，R1 和R2 的可靠性相当;1553B 总线可靠性为0.99999 时，当R ＞0.994，则R2 － R1 ＜0;1553B 总线可靠性为1 时，当R ＞0.999，则R2 与R1 的差值小于3.8 ×10－8，且随着R值的增大，两系统可靠性值的差异趋于0。R2 － R1随单机可靠性变化的2 条曲线见图10。运载火箭系统工程设计中需根据总线可靠性水平及可靠性指标、单机可靠性指标及其对系统可靠性的影响，确定合理的系统冗余容错结构。

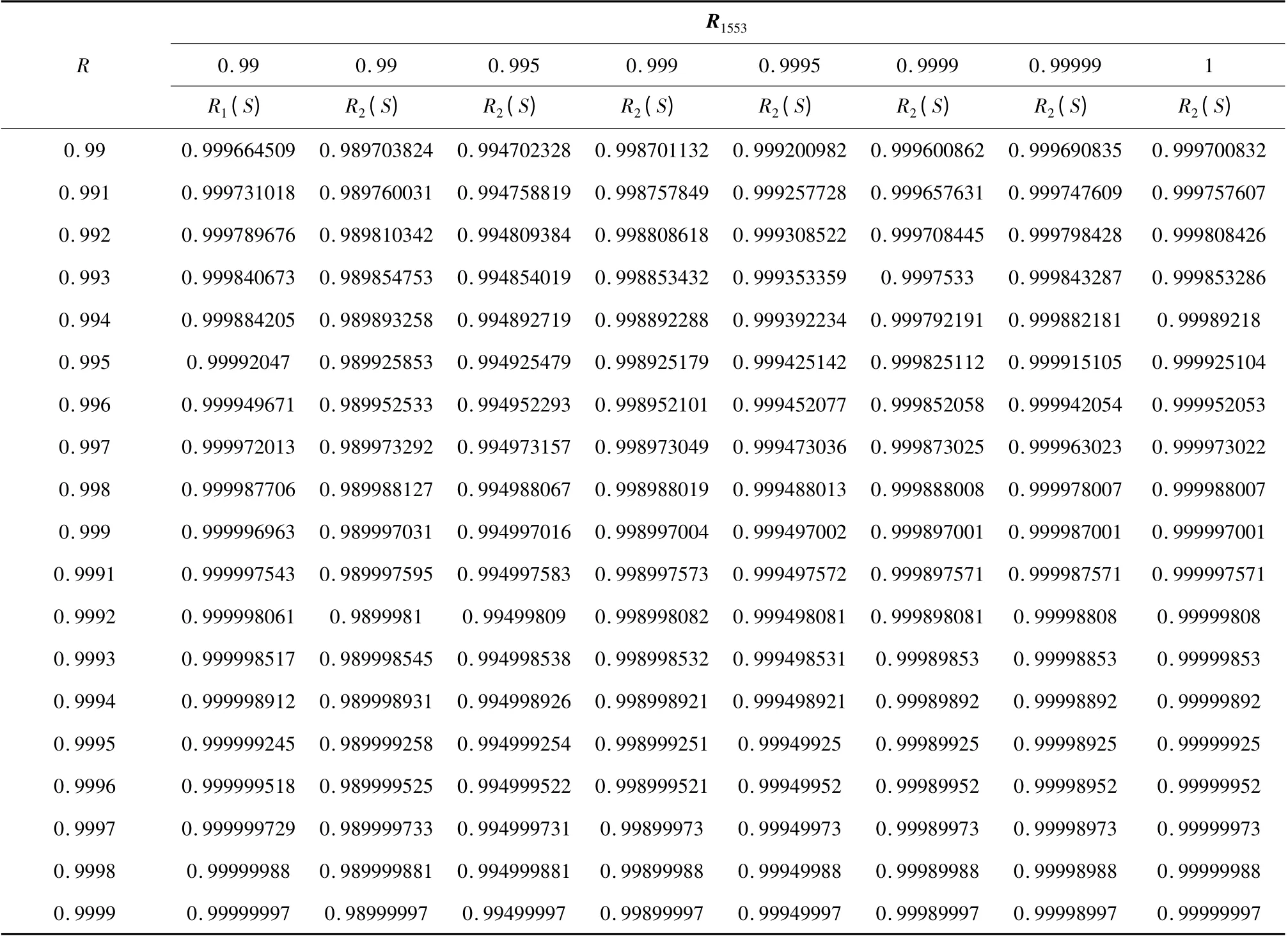
表1 复杂容错系统可靠性计算(Rsw =1)

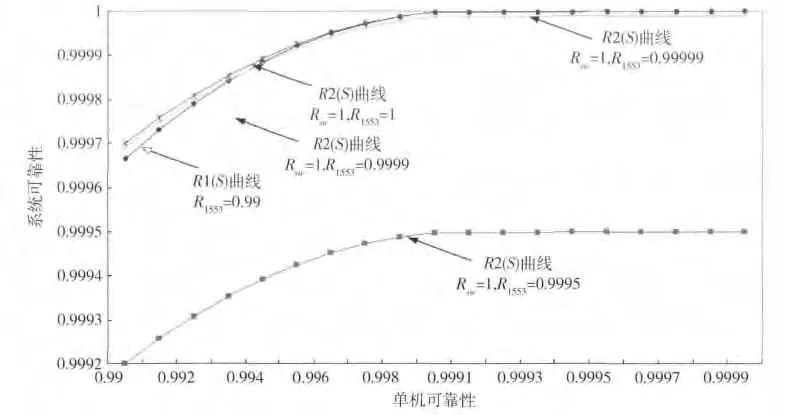
图8 系统可靠性随单机可靠性变化趋势图(Rsw =1)

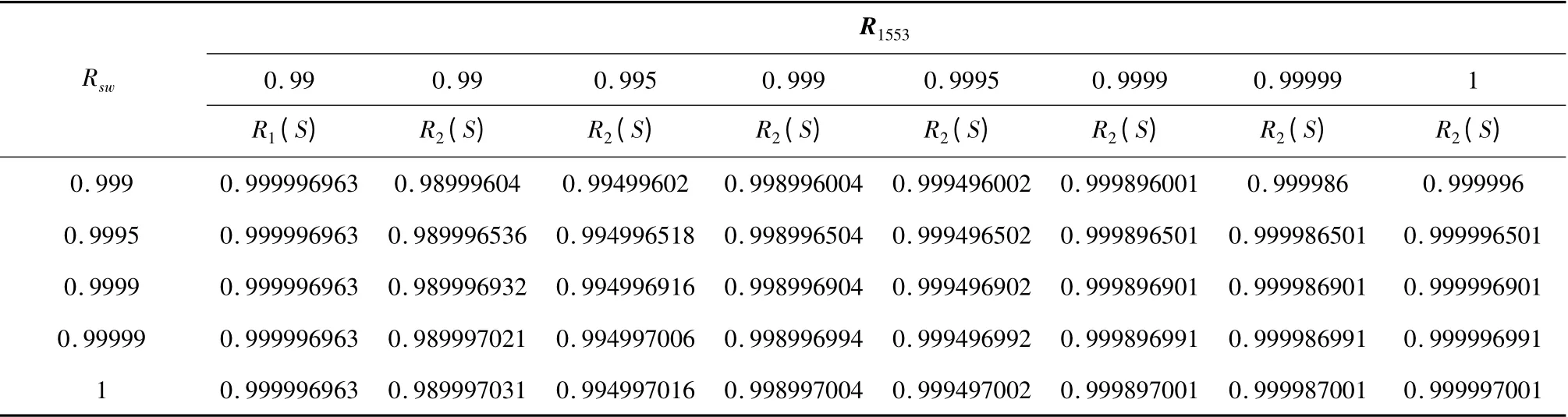
表2 复杂容错系统可靠性计算(R=0.999)

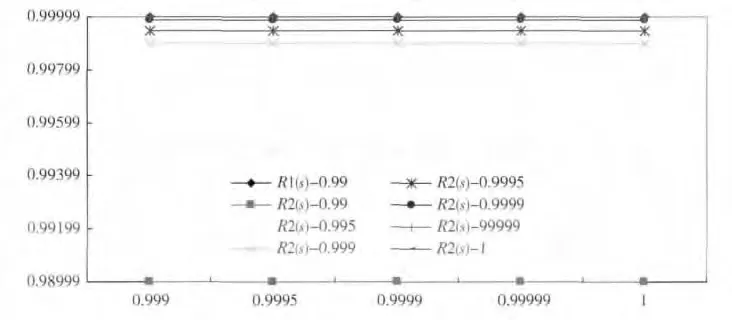
图9 系统可靠性随Rsw可靠性变化趋势图(R=0.999)

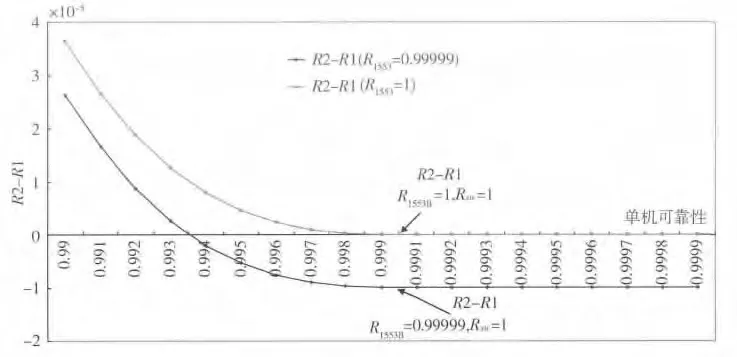
图10 R2 －R1 随单机可靠性变化的趋势图(Rsw =1)

总线切换开关的可靠性影响R2 系统可靠性，当BC 故障时，诊断、切换所需的时间很短以及由此带来的对系统功能性能的影响可以忽略时，分析总线切换开关的可靠性对系统可靠性的影响。考虑组成复杂冗余容错系统的单元模块或单机可靠性 R =0.999，根据表2 和图9，总线可靠性对R2 系统可靠性影响较大，总线开关在其可靠性大于0.999时对系统可靠性影响较小;总线可靠性为0.99 的R1 可靠性与总线可靠性为1 的R2 可靠性相当;总线可靠性为0.99 的R1 可靠性大于总线可靠性为0.99999的R2 可靠性。当R =0.999 时，以Rsw=0.999 为 起 点，Rsw取 值0. 999，0. 9995，0. 9999，0.99999和1，依次计算Rsw变化时系统可靠性的相对增长值，当总线开关可靠性大于0.999 时，其可靠性指标的提高对系统可靠性提升的贡献较小，最大不超过1 ×10－6。因此运载火箭系统工程设计中需根据总线开关切换复杂度及其可靠性水平，确定合理的总线切换方案。

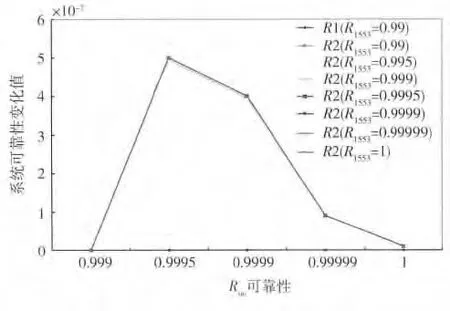
图11 系统可靠性随Rsw 变化的趋势图(R = 0.999)

4 结束语

冗余容错技术的使用，使得系统可靠性建模变得异常复杂。本文针对提高运载火箭控制系统可靠性的2 种容错设计方案，分析并建立了其可靠性定量分析的数学模型，然后进行了算例分析，从可靠性角度提出了运载火箭系统工程设计的建议，需根据总线可靠性水平及可靠性指标、单机可靠性指标及其对系统可靠性的影响，确定合理的系统冗余容错结构，同时根据总线开关切换复杂度及其可靠性水平，确定合理的总线切换方案。本文提出了运载火箭复杂容错控制系统可靠性分析的方法，并通过算例分析得出了一定条件下的结论，当条件不同时可能得出不同的结论，但均可采用本文方法进行可靠性建模分析，为控制系统可靠性评估、方案优化提供良好的支撑，本文方法能够在运载火箭控制系统工程设计中推广应用。

［1］孙凝生.冗余设计技术在运载火箭飞行控制系统中的应用(一)［J］. 航天控制，2003，(1):65-81. (Sun Ningsheng. The Redundancy Designs for Guidance and Control System of Launch Vehicle［J］. Aerospace Control，2003，(1):65-81).

［2］周正伐.可靠性工程基础［M］. 北京:中国宇航出版社，1999.

［3］周正伐，等.航天可靠性工程培训教材［M］.第1 版.北京:中国宇航出版社，2006.

［4］曾声奎，赵廷弟，等.系统可靠性设计分析教程［M］.北京:北京航空航天大学出版社，2001. (Zeng Shengkui，Zhao Tingdi，et al. The System Reliability Design and Analysis Tutorial ［M］. Beijing:Beihang University Press，2001.)

［5］杨振明.概率论［M］.2 版.北京:科学出版社，2004:34.

［6］马晓丽，张亮.全概率公式的推广及其在保险中的应用［J］.高等数学研究，2010，13(1):70-71.

［7］杨镝，张焰，祝达康. 特高压直流输电系统可靠性评估方法［J］. 现代电力，2011，28(4):1-6.(YANG DI，ZHANG Yan，ZHU Dakang. Reliability Evaluation Method for UHVDC Transmission System［J］. Modern Electric Power，2011，28(4):1-6.)

［8］丁明，王京景，宋倩.基于K/n(G)模型的柔性直流输电系统换流阀可靠性建模与冗余性分析［J］.电网技术，2008，32 (21):32-36. (DING Ming，WANG Jingjing，SONG Qian. Reliability Modeling and Redundancy Analysis of Converter Valves for VSC-HVDC Power Transmission System Based on k-out-of-n:G Model［J］. Power System Technology，2008，32(21):32-36.)

［9］Leelaruji R，Setréus J，Olguin G.Availability Assessment of the HVDC Converter Transformer System［C］. Proceedings of the 10thInternational Conference on Probabilistic Methods Applied to Power System，2008.

［10］丁明，毕锐，王京景.基于FD 法和模型组合的柔性直流输电可靠性评估［J］.电力系统保护与控制，2008，36(21):33-37. (DING Ming，BI Rui，WANG Jingjing. FD Method and Combined Model for Reliability Assessment of HVDC Flexible［J］. Power System Protection and Control，2008，36(21):33-37.)

［11］孙宇斌，刘文霞，等. 计及备用元件的柔性直流输电系统可靠性评估方法［J］.现代电力，2013，30(1):8-12.(SUN Yubin，LIU Wenxia，et al. The Reliability Evaluation Method for VSC-HVDC System by Considering of Standby Components［J］. Modern Electric Power，2013，30(1):8-12.)