基于多维振动特征的滚动轴承故障诊断方法

付云骁，贾利民，季常煦，姚德臣，李文球

(1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.北京交通大学 电气工程学院，北京 100044；3.广州地下铁道总公司，广州 510030)

滚动轴承作为机械设备中的关键部件，30%的机械故障是由轴承故障引起的[1]，需要诊断其状态来为分析机电系统的性能提供支持[2]。滚动轴承的故障复杂性体现在单元故障特征多样性以及单元的故障原因不唯一，并且轴承在早期故障时，异常信息比较微弱，很难被及时察知[3]。通过轴承故障诊断，定位轴承故障单元，对找出故障原因起着关键作用。

目前，滚动轴承故障特征可由多种方法提取。通常振动传感器采集滚动轴承运行时的振动信号，用时频分析的方法来提取故障特征，作为诊断滚动轴承故障的依据[4]。滚动轴承诊断所依据的特征有时域特征(Time-domain feature，简称TDF)[5]、频域特征[6,7]和时频特征[8]作为轴承诊断的特征向量。智能识别算法有基于决策树的诊断方法[9]，基于HMM的诊断方法[10]，基于SVM和模糊C均值聚类法[11]等。以上各自基于时域维度、频域维度和时频维度的特征提取算法，独立作为滚动轴承的故障特征参数进行模式识别，都能在一定程度上反映故障特征。但诊断精度均有待提高。

本文将TDF、IMF能量矩、IEM小波包能量矩和WPEM集合为特征矩阵，并按照各自诊断精度确定在矩阵中的权值，构成多维特征向量，分析滚动轴承的振动特点，对轴承信号的时域、频域和时—频域特征向量进行集合为多维特征矩阵。最后通过反向传播(BP)神经网络算法进行轴承状态识别，得到基于多维振动特征的滚动轴承故障诊断方法。

1 振动特征提取

1.1 时域诊断特征提取

滚动轴承振动信号的时域（也称幅域）统计参数具有计算量小，容易获得的特点，在故障诊断中可以作为特征参量进行分析，其中有量纲参数有均值、均方值、方差、均方差、概率密度函数、概率分布函数等。然而有量纲时域诊断参数其值在实际应用中很难进行区分，采用无量纲的时域参数能得到更好的分析效果[12]。本文提取峰值、峭度、脉冲、裕度、偏态五个无量纲参数作为要提取的时域统计特征参数，参数算法见文献[5，12，16]。

峰值指标随时间的变化趋势可以有效反应轴承缺陷的变化趋势。

峭度指标反映轴承信号偏离高斯分布程度。当振动信号中存在冲击性振动时其幅值会发生较大变化，而且随着故障的发展其值上升到一定程度反而会下降。峭度指标可以用于轴承的早期故障诊断。

脉冲指标对故障冲击性振动比较敏感，可作为有效的诊断参数。

裕度指标同样对冲击脉冲故障诊断有效，特别是在早期故障阶段时，会有明显增加。

偏态指标反应轴承信号幅值概率密度的不对称性。一般情况下，高斯随机信号的偏态指标为零，当偏态指标偏离零值较大时，轴承可能出现失效情况。

根据轴承故障的时域特性分析，以上特征参量作为时域维度特征辨识故障时，可以改善诊断结果的精度。

1.2 IEM提取

（1）EMD分解过程

IMF是对信号进行经验模态分解（Empirical Mode Decomposition，EMD）提取出来的。信号的EMD分解就是为了获得IMF。分解得到的每个IMF分量必须满足两个条件：

1)函数在整个时间范围内，局部极值点的个数和过零点的个数相等或相差不超过一个；

2)上下包络线关于时间轴是局部对称的，即在任意时刻点的局部极大值和局部极小值的平均为零。EMD的具体分解算法参考文献[6,13]。

IEM采用了计算IMF能量特征的方法，考虑了每个IMF能量在时间轴上的分布特点，能提取精确的信号本质特征[14]。IEM提取算法如下：

第一步：对降噪后的信号用EMD方法分解出有用的IMF分量；

第二步：根据式1计算离散的IEM

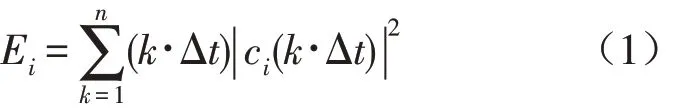
式中n为总的采样点数，k为采样点，Δt为采样周期。

第三步：构造归一化的能量矩特征向量。由于IEM数值较大，计算时的量会很大，采用归一化处理会方便计算分析。归一化过程如下式

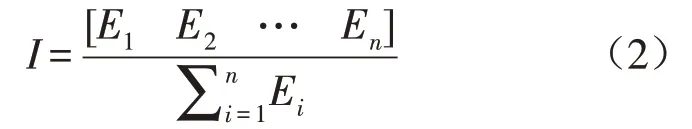
至此，IEM特征提取过程结束。

1.3 WPEM提取

基于小波包分解的故障诊断方法的核心就是通过小波包分解来提取振动信号能量集中的频带的信息分量[15]。小波包分解和重构算法参考文献[15,16]。小波包能量矩的提取方法同IEM提取方法相同，将提取的能量矩构造成向量P'=[ ]E0,E1,E2,...,Em，并将其归一化得到

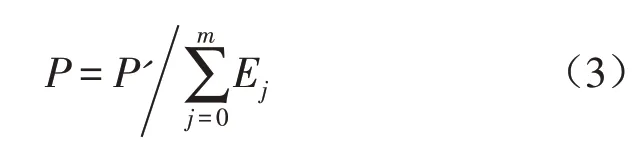
则P为所求的归一化后的WPEM的特征向量。

1.4 多维特征

由于不同状态的轴承信号单域维度某些特征值可能会有类间间距小，类内散度大的特点，甚至有交叉区域，因此诊断会出现特征盲区，为了提高诊断精度，消除盲区。多维振动特征矩阵集合了时域和频域的综合信息，提供了更丰富的状态判断指标，并且根据单维诊断精度设定多维特征向量不同维度的权值，增加同类测试特征落入正确状态域的概率，并且减少落入错误状态域的概率，从而改善诊断效果。

令T={Cf,Kv,If,Ma,Sf}为时域特征向量，式(2)得出的I为频域特征向量，式3得出的P为时频域的能量特征向量，则多维特征矩阵M=[ω1T，ω2I，ω3P]，ω1，ω2和ω3为单维特征的权值。权值设定为

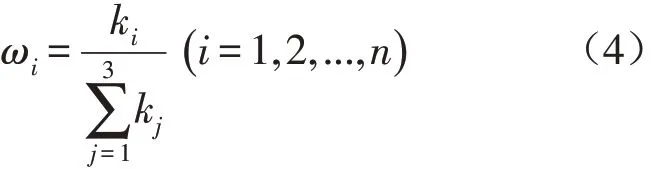
其中ki是单维特征诊断正确率，是四种状态的诊断效率的均值，i表示特征向量维度。图1所示为多维特征诊断流程，k是基于多维特征的故障识别精度，ω是特征域的权值。

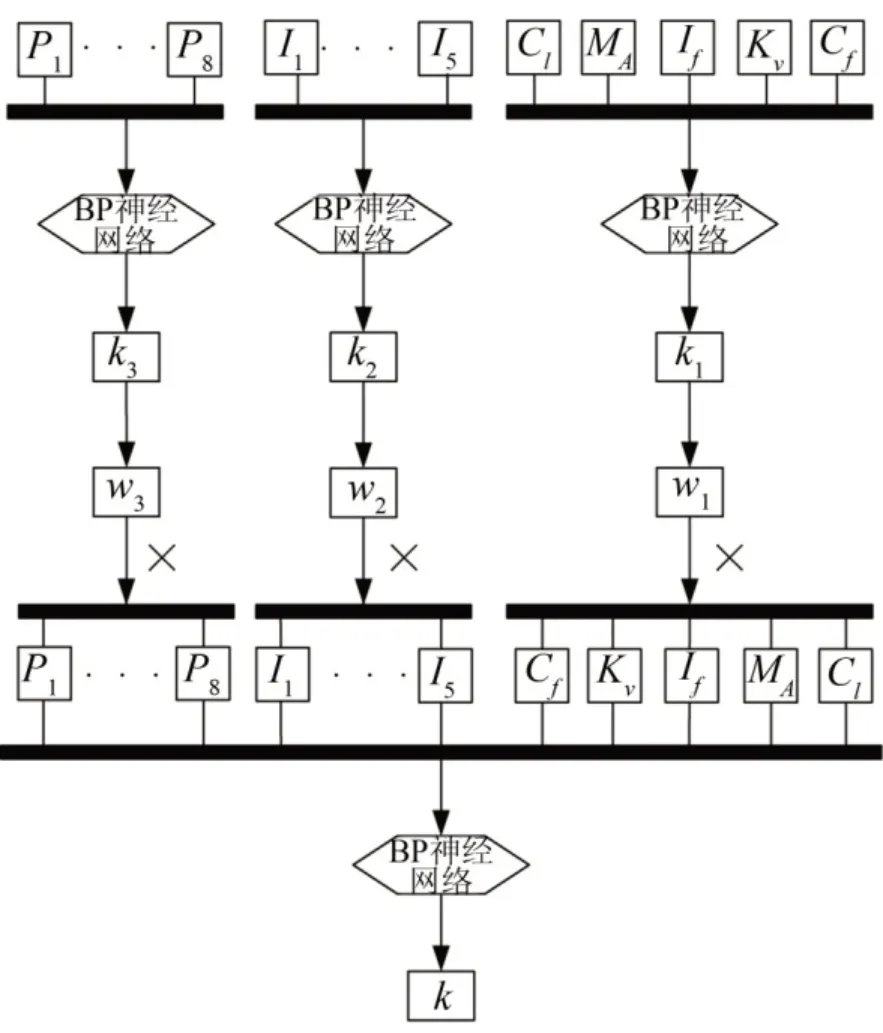
图1 多维特征诊断流程

1.5 BP神经网络[1133,1188,1199]

BP（Back Propagation）神经网络是一个成熟的智能算法，BP神经网络是对非线性可微分函数进行权值修正的多层网络,可以用在故障诊断中识别故障类型。它由输入层、隐含层、输出层组成。图2为BP神经网络结构的示意图。

2 智能诊断实验

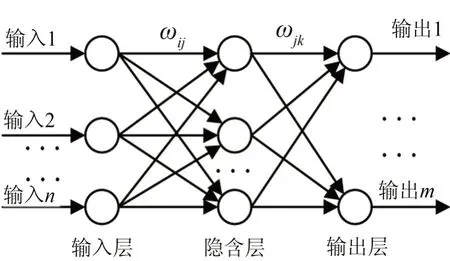
图2 神经网络结构图

本文提取机车电机驱动端实验轴承进行验证，用来区分滚珠故障、内环故障、外环故障以及无故障四种状态的轴承。四种实验轴承型号为205-2 RSJEM-SKF，采样频率均为12 kHz，转速均为1745 r/min，内环故障深度为0.178 mm，外环最外端的故障深度为0.178 mm，滚珠为点蚀故障，深度为14 mm。实验装置如图3，实验流程如图4，算法在Matlab环境下运行。

图3 轴承振动测试平台

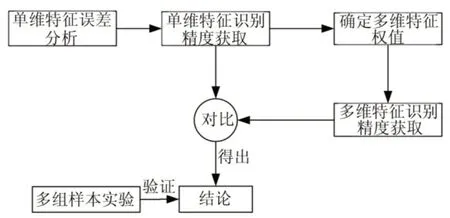
图4 实验流程图

2.1 单维特征变量误差分析

提取30组滚珠故障、内环故障、外环故障和无故障的轴承TDF、IEM和WPEM的统计信息分别见图5—7。分析可知不同故障发生时，TDF在时域的分布相差不太明显，直接用TDF分量来进行故障诊断会存在一定误差。从图6和图7中可以看出四种状况下的IEM和WPEM能量矩分量的值差异比较明显，可以进行初步故障诊断，但存在波动误差。

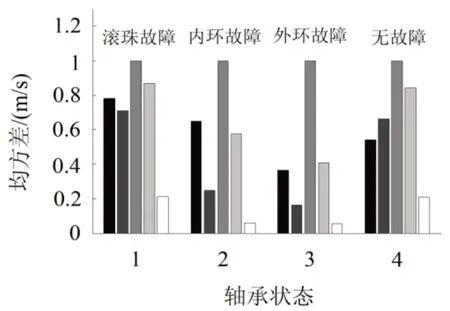
图5 TDF统计特征直方图

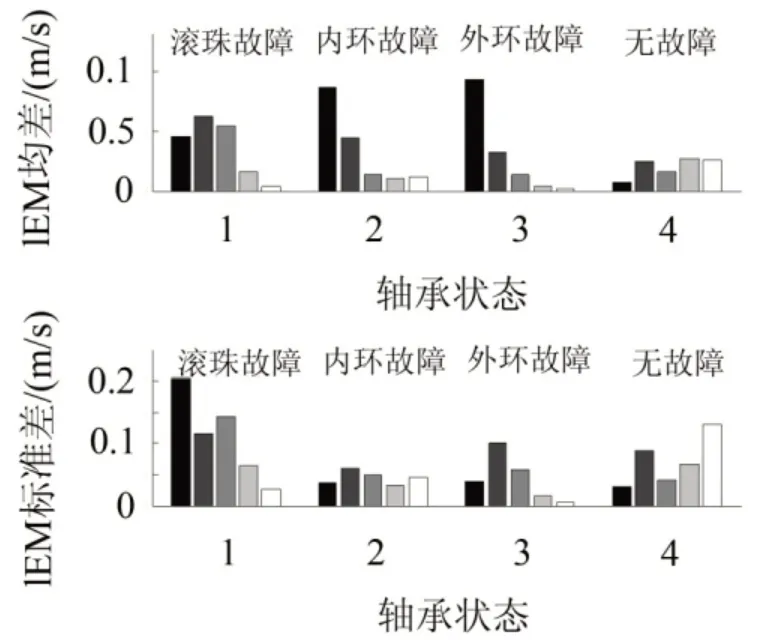
图6 IEM统计特征直方图

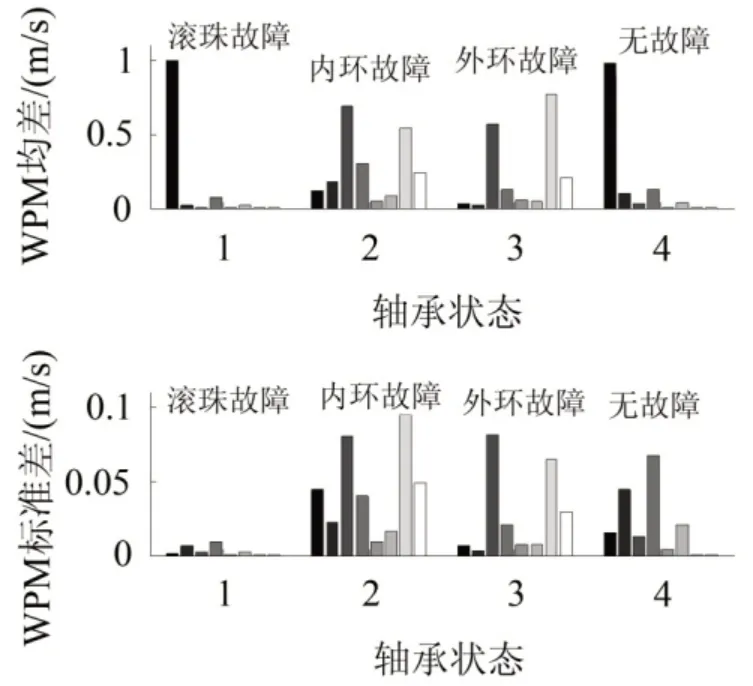
图7 WPEM统计特征直方图

2.2 诊断结果

用BP网络对神经所提取的30组实验数据的特征矩阵进行故障分类，针对每种状态下的轴承分别提取9组振动信号，作为测试数据。网络的迭代次数上限为3 000，最小误差限为0.05。诊断效果见表1。以神经网络的逼近最小误差限的迭代次数作为算法识别故障速率的指标，状态识别迭代结果见表2。

从表2中比较得出用TDF诊断指标识别的速率最慢；IEM和WPEM识别收敛速度相对较快。多维特征诊断，首先根据单维识别精度得到权值向量为[ω1ω2ω3]=[0.319 0 0.340 2 0.340 2]。基于加权多维特征诊断精度为：滚珠故障100%，内环故障100%，外环故障100%以及无故障88.9%。四工况的平均诊断精度为97.22%，多维特征—神经网络诊断误差走势见图8。多维特征—神经网络进行故障识别的迭代次数108高于WPEM诊断迭代次数26，但所用时间差别不大，故其速率差异可以忽略。而多维特征诊断的测试误差达到5×10-4远小于单维特征诊断的测试误差0.05，反映了基于多维特征的故障诊断方法更加高效。

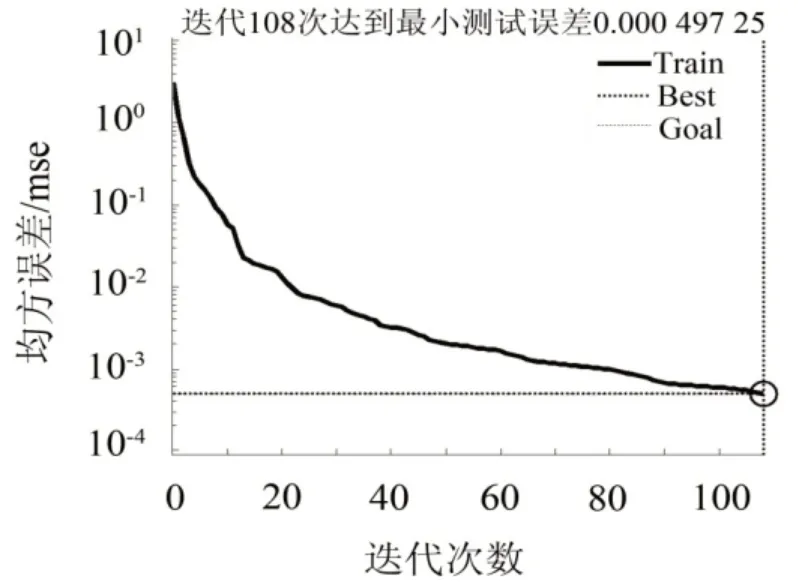
图8 多维特征诊断的迭代过程

表1 不同特征参量的故障诊断率

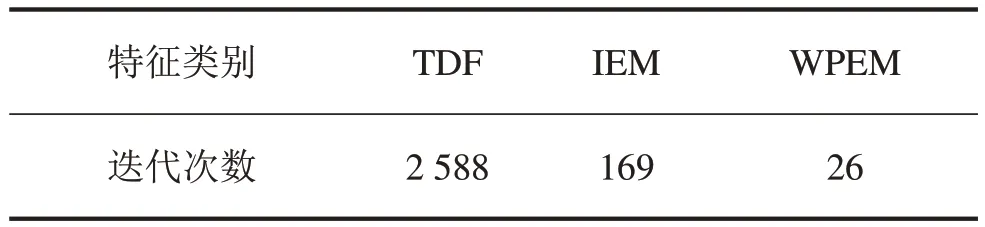
表2 单维特征—神经网络故障识别速率

2.3 实验验证结果

对于统计意义上的验证，多次用不同组数的数据作为训练数据，判断从少量训练样本不断增加的过程中，各方法诊断的精度和效率，实验中测试样本不变，为9组数据。结果如表3。

表3 不同组数训练样本下的平均故障诊断精度

多维故障特征矩阵作为故障诊断的依据，在小样本的情况下，能够做出较高精度的诊断，实验证明，基于时频域的多维振动特征参量的滚动轴承诊断方法的效率，比单维特征诊断明显提高。

3 结语

（1）基于IEM和WPEM的滚动轴承故障诊断方法，诊断速度快，诊断效率高，是相对可行的诊断方法；

（2）单维特征信息很难全面反映滚动轴承不同部位的故障本质，而将时域信息和频域的能量信息进行综合，形成时频域的多维特征故障诊断方法则对诊断有非常好的效果；

（3）在反映故障特征时，继续深入研究其他能够独立反映振动信号本质的特征参数，作为滚动轴承故障诊断的特征变量之一，丰富和完善诊断的特征依据，提高诊断效果的精确性。

[1]Chen Y D,Du R.Fault features of large rotating machinery and diagnosis sesor fusion[J].Journal of Sound and Vibration1995,188(2):227-242.

[2]陈长征，胡立新，周 勃，费朝阳.设备振动分析与故障诊断技术[M].北京：科学出版社.249-250.

[3]冯辅周，饶国强，司爱威.基于排列熵和神经网络的滚动轴承异常检测与诊断[J].噪声与振动控制，2013，33(3)：212-217.

[4]郑近德，程军圣，杨 宇.基于改进的ITD和模糊熵的滚动轴承故障诊断方法[J].中国机械工程，2012，23(19)：2372-2377.

[5]HUANG Zhong-hua,XIE Ya.Fault diagnosis method of rolling bearing based on bp neural network[C].2009 International Conference on Measuring Technology and Mechatronics Automation,2009,647-649.

[6]Bin G F,Gao J J,Li X J,Dhillon B S.Early fault diagnosis of rotating machinery based on wavelet packets-empirical mode decomposition feature extraction and neural network[J].Mechanical Systems and Signal Processing,2012,27:696-711.

[7]于德介，程军圣，杨 宇.Hilbert_Huang变换在滚动轴承故障诊断中的应用[J].22000033，14(24)：2140-2142.

[8]高 慧.基于卷积型小波包能量矩的机械故障特征提取[J].煤矿机械，2008，29(11)：198-200.

[9]M.Saimurugan,K.I.Ramachandran,V.Sugumaran,N.R.Sakthivel.Multi component fault diagnosis of rotational mechanical system based on decision tree and support vector machine[J].Expert Systems with Applications,2011,38,3819-3826.

[10]WU Bin,YU Shan-ping,LUO Yue-gang,FENG Changjian.Rolling bearing faults diagnosis method based on SVM-HMM[J].Measuring Technology and Mechatronics Automation,2010,3:295-298.

[11]夏均忠，苏 涛，安相璧，等.滚动轴承故障模式识别方法现状分析[J].噪声与振动控制，2013，33(4)：185-189.

[12]张 韧.旋转机械故障特征提取技术及其系统研究[D].杭州：浙江大学，14-15.

[13]杨 宇，于德介，程军圣.基于EMD与神经网络的滚动轴承故障诊断方法[J].振动与冲击，2005，24(1)：86-88.

[14]秦太龙，杨 勇，程 珩，薛 松.基于IEM和神经网络的轴承故障诊断[J].振动、测试与诊断，2008，28(3)：229-232.

[15]李世玲，李 治，李合生.基于小波包能量特征的滚动轴承故障监测方法[J].系统仿真学报，2003，15(1)：76-83.

[16]LI Xiao-feng,FU Yun-xiao,JIA Li-min.Fault diagnosis of railway axlebox bearing based on wavelet packet and neural network[J].Applied Mechanics and Materials,2012,226-228:749-755.

[17]刘海波，杨建伟，蔡国强，姚德臣.改进小波包与RBF网络在轴承诊断中的应用[J].机械设计与研究，2010，26(2)：92-95.

[18]杨 勇，程 珩，陈法法.基于小波包和BP神经网络的滚动轴承故障诊断[J].煤矿机电，2008，1：50-52.

[19]陈向东，赵登峰，王国强，许纯新.基于神经网络的滚动轴承故障监测[J].试验与分析，2003，2：23-26.