温度对橡胶隔振器力学性能的影响

刘迪辉，范 迪，欧阳雁峰，吴成平

（1.湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082；2.中联重科股份有限公司，长沙 410080）

隔振技术是振动与噪声控制的一种有效手段，为了抑制设备的有害振动，研究人员进行了大量的工作，近年来，在原有成熟的金属、橡胶等隔振器类型基础上发展起来的新型隔振器也层出不穷[1—3]。金属橡胶减振器、主动吸振减振器等新型减振器被应用于各种场合。但成本控制、技术不成熟等因素极大地限制了新型隔振器的应用，橡胶隔振器作为成熟的减振装置仍在工程实践中得到广泛应用[4]。

分动箱橡胶隔振器连接分动箱箱体和底盘，起到支撑分动箱和减振缓冲的作用，起主要减振作用的是其中的橡胶材料。对于橡胶隔振器在常温下的的动态试验，国内已有部分学者做过这方面的研究[5]，但橡胶隔振器中橡胶材料由于本身力学性能随温度的变化及变形受型腔的限制，会对橡胶隔振器的减振效果产生较大影响，进而影响分动箱的使用寿命。掌握橡胶隔振器力学性能随温度的变化规律，有利于设计人员根据其性能合理设置相关参数，减少事故的发生概率。

橡胶隔振器在实际使用过程中的振动为受迫振动，激振力的频率和振动的幅值对力学性能影响很大，测定振动元件在工作状态下的力学性能，不仅要求较为精确的振动频率控制，同时要精确地控制振动幅值[6]。所以用共振法和自由振动法难以准确地测定出减振元件的动刚度和阻尼系数等参数[7]。本文选用的电液伺服疲劳试验机对输入位移参数的频率和振幅控制精确，为后续数据分析和试验结论的得出奠定基础。

1 试验装置与步骤

1.1 试验装置

试验试件采用某型号泵车分动箱橡胶隔振器。内圈和外圈均为金属材料，中圈为橡胶材料，内圈金属嵌在橡胶中。橡胶隔振器剖面图如图1。

图1 橡胶隔振器力学性能试验夹具

实验中试件装夹在特定的夹具中，夹具将试验机提供拉力分别传递到橡胶隔振器的内圈和外圈金属，使橡胶材料变形，测量其力学性能，如图2。

图2 橡胶隔振器力学性能试验夹具

试验设备包括MTS 370电液伺服疲劳试验机（如图3）、MTS 561温度控制箱和数据采集系统等。通过温控仪改变环境的温度，并保持一定时间，使温控箱内温度均匀，通过疲劳试验机加载一定频率和振幅的正弦位移输入，得到相应状态下的载荷随时间变化的曲线。橡胶隔振器的振动为单自由度系统受简谐激振力下的强迫振动，根据机械振动学原理，系统的振动可以分为自由振动和受迫振动，其中自由振动的频率由隔振器固有频率决定，受迫振动频率由激励频率决定，由于阻尼的存在，实验进行若干时间，受迫振动将达到稳态，自由振动衰减。

1.2 试验步骤

结合橡胶隔振器实际工作时的状态，本次试验设定输入位移参数的频率为30 Hz振幅为0.5 mm，

图3 MTS 370电液伺服疲劳试验机

预拉伸位移为2 mm，拉伸方向为沿橡胶隔振器回转轴线方向的纵向拉伸，数据采集频率为1 000 Hz。试件安装入试验机后，取竖直向下为位移和载荷的正方向。试验中温控箱温度T1分别设定为25°C、50°C、75°C，以观察不同温度对橡胶隔振器力学性能的影响，每个单次试验在温度达到设定温度后，保持600 s，振动持续600 s，以消除橡胶隔振器固有频率对振动的影响。

2 试验原理

试件安装入夹具，并用试验机夹头夹紧后，开启MTS 561温控箱，调至设定温度，温度稳定后，给橡胶隔振器施加正弦位移激励，输入的正弦位移激励x(t)可表示为x(t)=X0sinωt+X1(1)其中X0为位移振幅，ω为激振角频率，X1为与最终试验计算结果无关的特定常数，t为试验时间。

振动达到稳定以后，得到的载荷随时间变化的曲线可以近似视为与输入振幅同频率正弦信号，载荷随时间的变化F(t)可表示为F(t)=F0sin(ωt+ϕ)+F1(2)其中F0为载荷振幅，ϕ为载荷与位移的相位差，F1为与最终试验计算结果无关的特定常数。

持续振动一定时间，以消除橡胶隔振器固有频率对试验的影响，记录采集到的载荷信号和实际的位移信号。理论上，在同一环境温度下，对分动箱橡胶隔振器加载固定幅值和频率的位移输入，其载荷波形与位移波形之间的相位差是一定的。

试验中采用动刚度Kd、相位差ϕ作为描述橡胶材料力学性能的指标[8,9]。橡胶隔振器的动刚度Kd可以表示为

为了提高本文中试验方法的适用性，降低试验对疲劳试验机类型等特定试验设备的依赖，采用“拟合法”测量相位差。调用MATLAB中的cftool函数，将采集到的载荷和真实位移随时间变化的数据拟合为一阶傅里叶三角函数展开式如

其中a0-3，b1,2为拟合参数。

将位移、载荷的振幅带入式(3)得到动刚度Kd

由三角函数的相位公式，可得位移与载荷的相位差，阻尼系数C可以用动刚度和相位差表示

将相位差和动刚度带入式（7）得

式(8)即为橡胶隔振器阻尼系数表达式，可以看出，阻尼系数只与振动的圆频率以及拟合后的四个参数有关，只要获得这些参数，即可计算得到阻尼系数。

3 数据处理与分析

将本试验中关键的物理参数列入图4。X为疲劳试验机夹头的位移。T1为温控箱中的试验环境温度，在试验中固定地设定为25°C、50°C和75°C。T2为橡胶隔振器中某一点的温度，由于持续振动，试验中这一温度会随着时间的推移而逐渐增加。

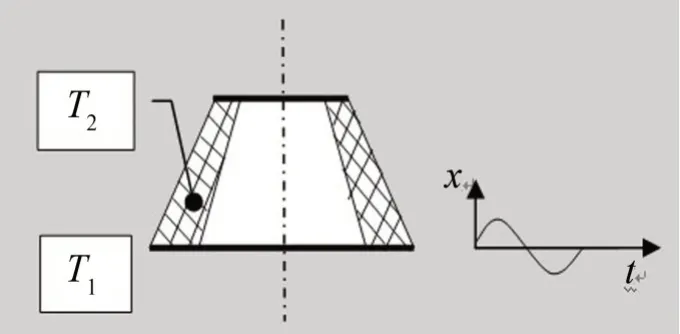
图4 试验中的关键物理参数

3.1 数据处理

MTS液压伺服测试系统的数据采集器将实验得到的时间、位移、载荷等数据采集并存储为离散序列。将得到的离散序列导入MATLAB，可以分别得到振动的位移—时间曲线和载荷—时间曲线，所得数据只需要橡胶隔振器振动稳定后的部分，且同一温度下，振动稳定后数据相位、振幅等基本不变。25°C下，分别取第500 s至第501 s振动的位移—时间曲线和载荷—时间曲线如图5，6，调用cftool函数分别挑选橡胶隔振器振动稳定后的位移—时间曲线和载荷—时间曲线中的同一时间区间进行拟合，目标函数为一阶傅里叶三角函数展开式。其中载荷—时间曲线的拟合结果如图7。

图5 25°C下橡胶隔振器部分位移—时间曲线

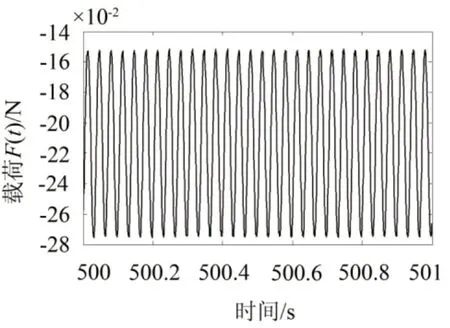
图6 25°C下橡胶隔振器部分载荷—时间曲线

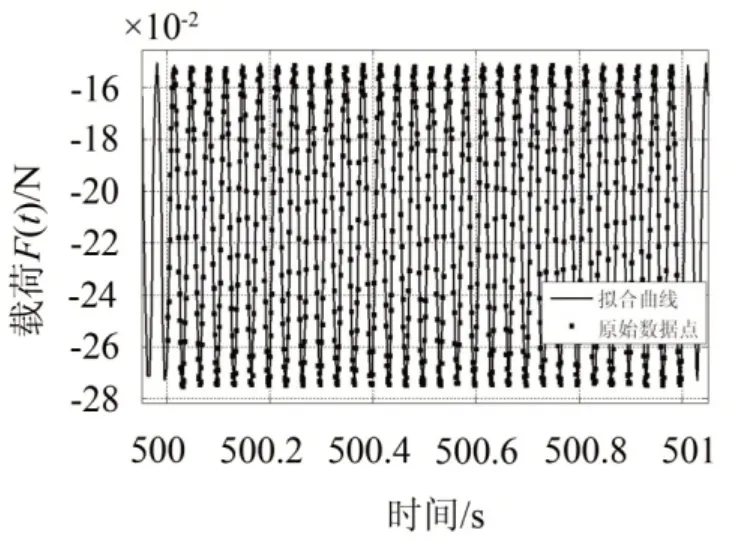
图7 拟合的25°C下载荷—时间曲线

从图中可以看出，以1阶傅里叶三角函数展开式为目标函数进行拟合，可以使拟合曲线穿过绝大多数原始数据点，使得到的拟合曲线更接近真实数据曲线。

每次试验取其中三个相同时间段t1(500 s～501 s)、t2(550 s～551 s)、t3(590 s～591 s)，对试验获得的数据进行拟合处理，将得到的拟合参数带入式(6)和(8)，得到表1。

表1 动刚度、阻尼系数试验测量结果

3.2 数据分析

考察温控箱温度对橡胶隔振器动刚度和阻尼系数的影响，由表1可以看出，随着环境温度的增加橡胶隔振器的动刚度和阻尼系数逐渐减小，且阻尼系数减小明显。环境温度达到75°C时，橡胶隔振器的动刚度是25°C时的70%左右，阻尼系数仅为25°C时的15%左右。三个温度下的动刚度和阻尼系数变化如图8，9所示。

图8 动刚度Kd随温控箱温度变化情况

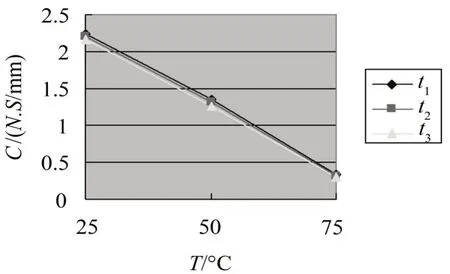
图9 阻尼系数C随温控箱温度变化情况

试验选取三个时间段有先后之分，橡胶隔振器振动中产生的热量随着时间提升，隔振器内部的温度也随之升高，这将影响橡胶隔振器的动刚度和阻尼系数，三组不同温度的试验中橡胶隔振器动刚度和阻尼系数在三个选取的时间段内的变化如图10,11所示。

图10 动刚度在三个时间段内的变化

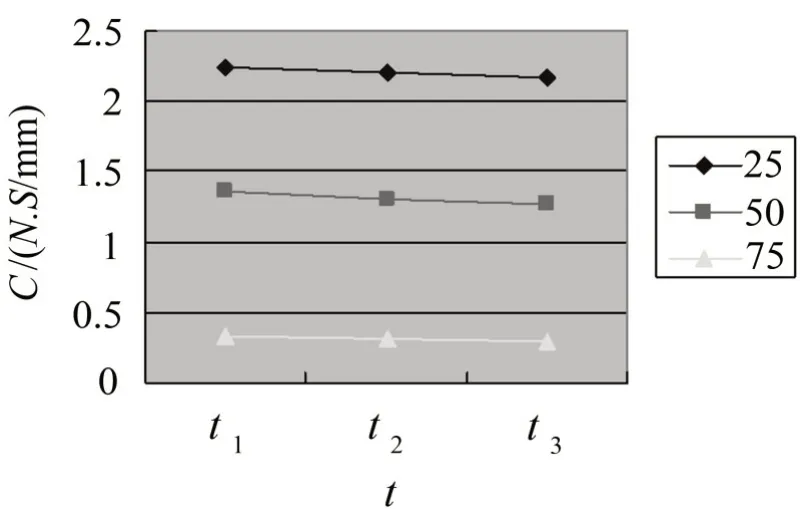
图11 阻尼系数在三个时间段内的变化

由图10，11可以看出，同一环境温度下，随着振动的持续，橡胶隔振器的动刚度和阻尼系数均有降低，但t1，t2，t3三个时间段内的变化并不明显。

4 结语

(1)提出了一种研究温度对橡胶隔振器力学性能影响的试验方法。开发了一套专门用来夹持橡胶隔振器的夹具，并将夹具和试件置于温控箱中，直接测试不同环境温度下隔振器的动刚度和阻尼系数；(2)橡胶隔振器的动刚度和阻尼系数随着温度的升高而减小，其中环境温度对其影响较大，由隔振器振动产生的温升也对其有一定影响。在上面测试条件下，当环境温度达到75°C时，橡胶隔振器的动刚度是25°C时的70%左右，阻尼系数仅为25°C时的15%左右。

[1]Keith K.Denoyer,Conor Johnson.Recent achievements in vibration isolation systems for space launch and on-orbit applications[J]. International Astronautical Congress Toulouse,,2001(10):32-36

[2]Yunhe Yu,Nagi G.Naganathan,Rao V.Dukkipati,A literature review of automotive vehicle engine mounting systems[J].Mechanism and Machine Theory,vol.36,2001,pp.123-142.

[3]Ellison J.Passive vibration control of airborne equipment using a circular steel ring[J].Journal of Sound and Vibration,,2001,246(1):1-28.

[4]孙 伟，李以农，刘万里，等.橡胶隔振器非线性动态特性建模及实验研究[J].振动与冲击，2012，23(23)：71-76.

[5]张 彬，庄国华，曾向荣.橡胶减振器蠕变的试验研究[J].噪声与振动控制，2008，(4)56-59.

[6]王建国，王连庆，王红缨，徐世平.汽车发动机支承软垫动态刚度与阻尼的测试[J].物理测试，1999，(5)：23-27.

[7]张阿舟，姚起杭，等.振动控制工程[M].北京:航空工业出版社，1989．

[8]吕振华，梁 伟，上官文斌.汽车发动机液阻悬置动特性仿真与实验分析[J].汽车工程，2002，24(2)：105-111.

[9]龚宪生，谢志江，骆振黄，等.非线性隔振器阻尼特性研究[J].振动工程学报，2001，14(3)：336-338.