基于相空间重构和遗传优化SVR的机械设备状态趋势预测

王 涛，李艾华，高运广，蔡艳平，王旭平

（第二炮兵工程大学 机电工程系，西安 710025）

由于表征机械设备运行状态的振动信号特征量呈现出较强的非线性、非平稳特点[1]，因此基于振动信号的机械设备状态预测是一个典型的非线性时间序列预测问题。目前，常用的非线性预测模型主要有：时序模型、灰色模型以及人工神经网络模型，以上方法在小样本学习方面均存在缺陷。支持向量回归（Support Vector Regression，SVR）继承了支持向量机在小样本学习方面的优点[2]，因而被广泛应用于复杂时间序列的回归与预测。但要想得到满意的预测精度，既与SVR的输入特征有关，还与SVR模型参数的选取紧密相关。

在将支持向量回归机应用于机械设备状态预测时，特征选择是一项至关重要的工作。目前，常用的方法是人为确定训练SVR预测器的输入和输出矩阵，采用均方根误差、均方误差或者相对误差对模型的逼近能力和预测效果进行评估[3-—5]。这种方法的不足之处是训练数据的选取缺乏理论指导，一旦选定就只能通过预测值与真实值之间的误差来反复修正模型，直到得到满意的预测精度，导致训练时间长，容易产生过拟合现象。

另外，当核函数确定后，支持向量回归机的性能优劣取决于惩罚因子C、不敏感系数ε以及核参数σ（本文默认采用高斯核函数）的选择。常用的SVR参数选择方法有经验法、格搜索结合交叉验证法。前一种方法太主观，后一种方法很费时，并且总体上其选择参数的方法还是盲目的，不能实现参数的全局统一调节，只能一个一个的调节。目前，已有很多学者将智能优化算法应用于SVR模型选择之中。文献[6]组合格搜索和10重交叉验证法对SVR模型参数进行优化选择；文献[7]分别采用进化编程方法和粒子波算法优化SVR模型参数；文献[8]提出一种采用改进协方差矩阵的进化策略优化SVR模型参数；文献[9，10]分别应用免疫算法和差分进化算法优化SVR模型参数；文献[11]采用遗传算法优化SVR模型参数。其中，遗传算法作为一种通用的智能全局优化算法，采用它优化SVR模型参数，不仅能保证寻优结果的全局特征，而且克服了人工反复“试凑”的主观性。

鉴于此，本文采用相空间重构技术自适应选取SVR输入特征，采用自适应遗传算法同步优化SVR模型参数，在此基础上构建了一种基于相空间重构与遗传优化SVR的预测模型，并将其应用于某炼油厂烟机状态预测。

1 相空间重构选择输入特征

为了避免训练数据选取的盲目性，提高模型学习效率，本文将相空间重构技术引入到机械设备状态预测中，通过将一维振动信号时间序列转化成矩阵形式，以相点作为输入特征训练SVR预测器，实现了输入特征的自适应选取。

对于时间序列{xi,i=1,2,...,n}，n为序列的长度。根据Takens提出的嵌入定理[12]，重构相空间为{xi,xi+τ,...,xi+(m-1)τ}，i=1,2,...,M。式中xi为相空间的点；m为嵌入维数；τ为延迟时间；M为重构相空间中相点的个数，M=n-(m-1)τ，相空间的吸引子矩阵为

相空间重构技术的核心在于选择合适的嵌入维数m和延迟时间τ。目前，选取延迟时间τ的方法主要有自相关函数法、最小互信息法、平均位移法等。其中，自相关函数法在实际中应用较多，但自相关函数法仅能提取时间序列间的线性相关性，且很难应用于高维混沌系统，因此不适用于机械设备状态的非线性时间序列预测问题。最小互信息法[13]克服了自相关法的缺点，包含了时间序列的非线性特性，其计算结果明显优于自相关法，并取互信息函数的第一个极小值点作为优化的延迟时间τ。因此，本文选择最小互信息法确定最佳延迟时间τ。选择最小嵌入维数m的常用方法主要有关联指数饱和法、奇异值分解（SVD）法、虚假邻域法等。其中，以虚假邻域法应用最为广泛，但虚假邻域法在有噪声存在时效果往往较差。为了克服这一缺点，CAO Liang-yue于1997年提出了一种基于虚假邻域法的改进方法，称之为CAO方法[14]。本文选择CAO方法确定最小嵌入维数m。需要注意的是，在使用CAO方法确定嵌入维数m前，需要预先确定最佳延迟时间τ。

2 遗传优化SVR模型参数

当采用ε-SVR算法构造预测模型时，通过控制C和ε两个参数，可以控制支持向量机的推广能力。其中，不敏感参数ε控制SVR模型的复杂程度。增大ε值则支持向量数目减少，导致预测模型过于简单，学习精度不够，造成欠拟合；减小ε值则支持向量数目增多，回归精度提高，但可能导致SVR模型过于复杂，且训练时间也会增加，得不到好的推广能力，造成过拟合。惩罚因子C控制SVR模型的鲁棒性。参数C在结构风险和样本误差之间作出折中，以便使SVR模型有较好的推广能力。C取值大则学习精度相应提高，但模型的泛化能力变差。C取值小则对样本数据的惩罚小，可能导致训练误差变大。此外，C值影响SVR模型对异常点的敏感度，选择合适的参数C可在一定程度上抗干扰，从而保证模型的稳定性。当训练SVR模型时，如果采用高斯核函数，则核参数σ会对模型的预测准确程度产生很大影响。核参数σ太小，估计的回归曲线会较为粗糙，易出现“过拟合”；σ太大，则回归曲线较为光滑，易出现“欠拟合”。总之，σ取值太大或太小都会使SVR模型的泛化性能变差。

为了克服人工选择参数存在盲目性和随意性的问题，本文采用自适应遗传算法优化SVR模型参数，实现了模型参数自动寻优。由于相对误差（MAPE）比较客观地体现了预测误差与真实值的大小，因此本文采用MAPE指标作为SVR模型预测性能的评价指标，遗传算法的适应度函数定义为

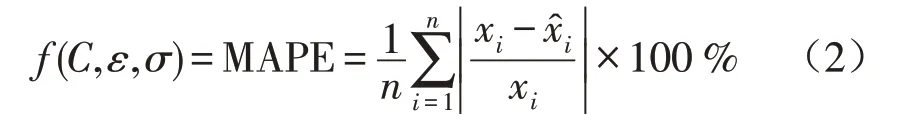
基于自适应遗传算法的SVR参数优化步骤如下：

Step1：迭代次数t=0；

Step2：随机选择实数编码的初始种群P(t)；

Step3：针对P(t)中的个体训练SVR，计算个体适应度函数值f(t)；

Step4：若种群中最优个体所对应的适应度函数值满足要求或达到设定的迭代次数，则转到Step7；

Step5：t+1；

Step6：应用选择、交叉以及变异算子产生新的种群，之后转到Step3；

Step7：给出最佳的C、ε以及σ参数，并在训练数据集上训练最佳回归模型。

3 基于相空间重构与遗传优化SVR的状态预测模型

本文所提方法的具体过程描述如下：

（1）将反映机械设备状态的原始振动数据或经过特征提取后的特征样本构造成一个单变量时间序列{x1,x2,...xn}，然后采用相空间重构技术将时序数据转换为矢量数据，确定延迟时间τ和嵌入维数m。

（2） 取 {xn}为 预 测 目 标 值 ，将{xn-1,xn-2,xn-3,xn-m}作为相关量，建立输入xn={xn-1,xn-2,xn-3,xn-m}与输出yn={xn}之间的映射关系：Rm→R，构造用于支持向量回归机的学习样本为

（3）采用自适应遗传算法对组合参数(C,σ,ε)进行优化，并基于优化参数训练SVR回归模型为

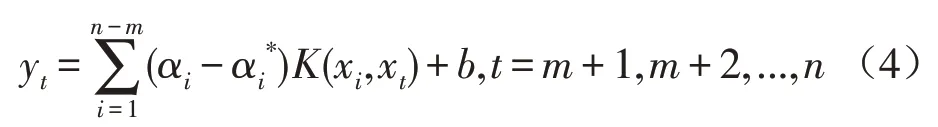
得到第n+1点的预测模型为

（4）一般，第p步预测模型为

xn和分别表示第n个数据的实际值和预测值。

4 某机组振动的回归与预测结果及分析

某炼油厂重油催化裂化装置（简称重催）由烟机、风机、齿轮箱和电机四个部分组成，机组的结构简图如图1所示。该机组是炼油厂的重点设备之一，其运行安全可靠性对提高炼油厂的经济效益具有十分重要的意义。因此，对该机组的运行状态趋势进行预测十分必要。

图1 某机组结构及传感器布置图

为了监测和评估该机组的运行状态，分别在烟机和风机两端轴瓦处安装了电涡流传感器，连续获取各轴瓦处轴的振动位移信号。从这些信号中，每隔一小时提取一个振动位移值，组成一个单变量时间序列，对这个时间序列的预测就是对该机组在某个位置振动状态的预测。在这个序列里选取120个点（5天的数据）作为回归训练样本，建立回归和预测模型，如图2所示。

基于本文所提方法建立预测模型之前，需要对时间序列进行相空间重构。首先采用最小互信息法计算得到延迟时间τ=1，然后采用CAO方法计算得到最小嵌入维数m=7，如图3所示，E1用于确定最小嵌入维数m，E2用于判定时间序列是否为确定性序列。

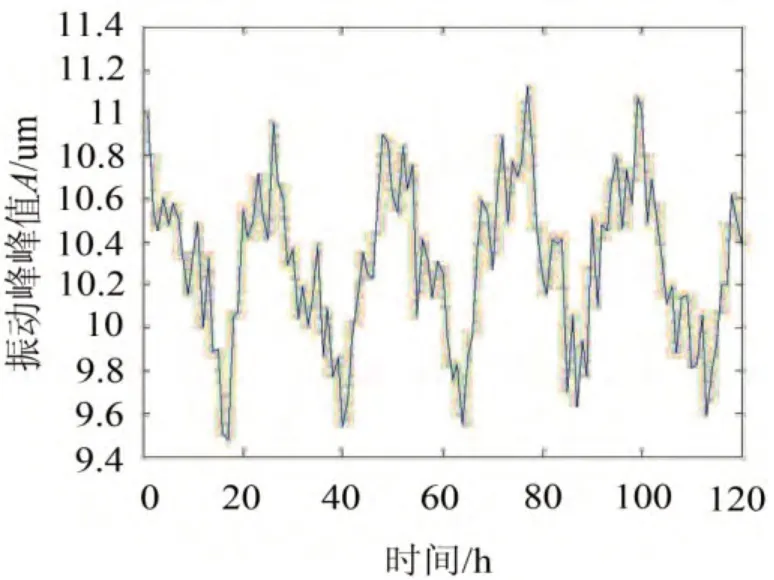
图2 某机组振动位移值原始信号

图3 采用CAO方法计算最小嵌入维数

将120个数据分成两部分，其中前96个数据用来训练模型及优化模型参数，剩余24个数据用来验证模型的有效性。利用自适应遗传算法优化模型参数(C,σ,ε)，其中优化算法的参数设置如表1所示，进化过程及迭代结果如图4所示。

经自适应遗传算法优化搜索得到惩罚因子C的值为160.692 8，高斯核参数σ的值为4.529 5，不敏感参数ε的值为0.006 5，对应的最佳适应度值为0.999 6。

为了验证本文所提基于相空间重构和遗传优化SVR预测模型的有效性，使用上述优化得到的参数值对机组振动时序前96个数据点进行拟合。同时，为了与标准SVR模型比较，人工设定参数C=100，高斯核参数σ=9，不敏感参数ε=0.007，训练标准SVR模型。遗传优化SVR模型和标准SVR模型对机组振动时序的回归结果如图5所示，图中黑点表示实际振动序列点，红色实线表示遗传优化SVR模型对振动时序的回归曲线，黑色点划线表示标准SVR模型对振动时序的回归曲线。

图4 优化过程及结果

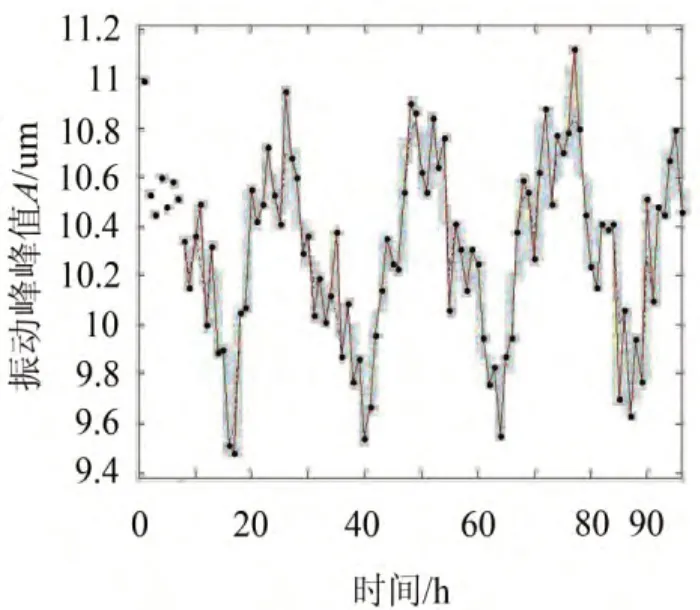
图5 遗传优化SVR回归结果

从图5可以看出，两种模型的回归曲线与实际曲线非常吻合，回归误差小，回归精度高。两种模型对振动时序的回归误差如表2所示。

分别采用单步预测和多步预测方法对以上两种模型的性能进行研究。在单步预测时，每次预测都以待预测点附近的一些样本值作为训练集，将测试点输入训练好的回归模型中，对下一时间点进行预测。在多步预测时，直接将前一次模型预测值作为下一时刻预测的输入向量元素，对下一时间点进行预测。

用剩余的24个数据点对模型的预测能力进行检验，遗传优化SVR模型和标准SVR模型对上述振动时序的单步预测和24步预测结果分别如图6和图7所示，两种模型对振动时序的单步预测误差和24步预测误差分别如表3和表4所示。

表1 自适应遗传算法参数设置表

表2 两种预测模型的回归误差

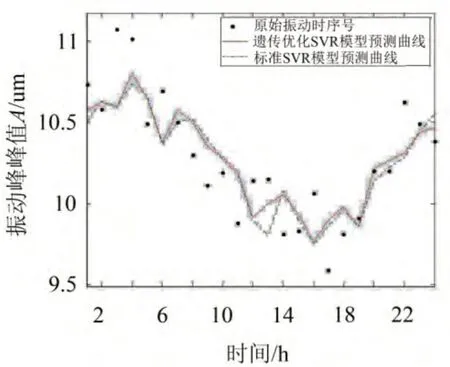
图6 单步预测结果

图7 24步预测结果

由上述实验结果可知，无论是单步还是24步预测，遗传优化SVR模型的预测精度都要比标准SVR模型的预测精度高。同时，遗传优化SVR模型的单步和24步预测精度都比较理想，而标准SVR虽有较好的单步预测效果，但多步预测能力明显低于遗传优化SVR模型，这说明本文所提预测方法对该重油催化裂化装置状态预测是非常有效的。

表3 两种预测模型的单步误差

5 结语

针对机械设备振动信号序列的非线性、非平稳性特点，本文构建了基于相空间重构与支持向量回归机的预测模型，并采用自适应遗传算法对模型参数进行优化。实验表明，所提方法预测精度高，推广能力好，为解决机械设备状态预测问题提供了一种新思路。本文主要结论如下：

（1）为了避免输入SVR的信息不足或冗余，通过相空间重构法自适应选取特征，以相点作为输入特征训练SVR预测器，有效避免了数据选取的盲目性，提高了模型的学习效率；

（2）为了克服人工选择参数存在盲目性和随意性的问题，采用自适应遗传算法优化SVR模型，使模型参数由人工优选变为自动寻优，有效提高了预测模型的泛化推广能力和训练速度；

（3）某炼油厂烟机状态预测结果表明，无论单步还是多步预测，遗传优化SVR模型的预测效果均优于标准的SVR预测模型。

[1]YANG Bo-suk,Widodo Achmad.Support vector machine for machine fault diagnosis and prognosis[J].Journal of System Design and Dynamic s,2008,2(1):12-23.

[2]Vapnik V N.Statistical learning theory[M].New York:John Wiley ＆ Sons,1998:10-40.

[3]侯澍曼，李友荣，刘光临.基于支持向量机的设备振动信号趋势预测[J].湖北工业大学学报，2006，21(3)：12-17.

[4]王红军，张建民，徐小力.基于支持向量机的机械系统状态组合预测模型研究[J].振动工程学报，2006，19(2)：242-245.

[5]杨晓红，杨晓静，朱霄珣.小波变换的支持向量回归机振动数据短期预测[J].汽轮机技术，2011，53(1)：77-80.

[6]Venkat R.Nadadoor,Hector De la Hoz Siegler,Sirish L Shah,William C Mc Caffrey,Amos Ben-Zvi.Online sensor for monitoring a microalgal bioreactor system using support vector regression[J].Chemometricss and Intelligent Laboratory Systems,2012(110):38-48.

[7]Sancho Salcedo-Sanz,Emilio G.Ortiz-García,Ángel M.Pérez-Bellido,Antonio Portilla-Figueras,Luis Prieto.Short term wind speed prediction based on evolutionary support vector regression algorithms[J].Expert Systems with Applications,2011(38):4052-4057.

[8]HOU Shu-min,LI You-rong.Short-term fault prediction based on support vector machines with parameter optimization by evolution strategy[J].Expert Systems with Applications2009(36):12383-12391.

[9]聂建元，余晓鸿.免疫支持向量机在故障测距中的应用[J].华中电力，2011，24(3)：94-98.

[10]陈 涛.基于差分进化算法的支持向量回归机参数优化[J].计算机仿真，2011，28(6)：198-201.

[11]HUANG Ji,BO Yu-cheng,WANG Hui-yuan.Electromechanical equipment state forecasting based on genetic algorithm-support vector regression[J].Exxppeerrtt Systems with Applications2011(38):8399-8402.

[12]Takens F.Detecting strange attractor in turbulence[J].Lecture Notes in Mathematic s,1981,898(2):361-38l.

[13]Fraser A M,Swinney H L.Independent coordinates for strange attractors from mutual information[J].Physs RReevv A,1986,33(2):1134-l140.

[14]CAO Liangyue,Mee A,Judd K.Dynamics from multivariate time series[J].Physiiccaa DD,1998,121(1-2):75-88