两种不同剖分方式的声线束追踪法声衰减计算

王海波，余 志，蔡 铭

(中山大学工学院 广东省智能交通重点实验室,广州 510006)

声线束追踪法(Beam Tracing Method(BTM))是一种解决声波遇到障碍物反射和衍射问题的重要方法[1]。障碍物较多时，由于声线束追踪法需要模拟声波向四周发散的过程，计算量较大[1，2]。为此，需要进行空间剖分对相应空间进行剖分以降低计算量。对于声波在复杂的环境中快速地完成递归几何运算，国外部分学者提出了先将计算区域进行子空间划分，再采用声线束追踪法和镜像法相结合的办法[3]。还有学者采用二分空间法（Binary Space Partition）[4]对所在空间预处理成凸多边形，在有序的凸多边形环境中进行声线束追踪[5，6]。国内也有对三维空间声传播正三棱锥前向伸展算法[7]和差值算法的研究[8，9]。另外，罗威力等提出了一套动态交通噪声模拟方法，应用Delaunnay三角剖分对二维空间进行了剖分快速生成声线束路径[10]。这些研究在算法上提出空间剖分方法，处理一些实际问题，但均没能解决大区域全三维空间复杂声传播的问题。

空间剖分是处理复杂空间结构并提供拓扑连续性建模的重要手段[11]，广泛应用于图像处理[12]和三维实体建模[13]等领域，尚未在文献中发现被应用于三维声线束追踪的路径生成。本文采用两种剖分方式把空间剖分成三棱柱和四面体空间网络，把需要全局搜索的声线束追踪转换为局部搜索，从而起到加速追踪声线束追踪的作用。在生成基本空间结构后，递归地构建声线束树形结构。对每一对声源点和接收点，通过声线束追踪法在生成声音传播路径并应用声音传播衰减模型进行计算。本文处理两种剖分的实际问题，分析两种方法的时间复杂度，通过实验对算法的准确度和可行性进行验证，对两种方法的计算精度进行比较，并对方法的适用性、局限性和误差进行讨论。

1 三维空间剖分

通过空间剖分、声线束追踪和路径生成三个阶段来确定声音的具体传播过程。

空间剖分将含有障碍物的空间剖分成基本结构体网格，使声线束追踪过程从全局缩小为局部，加速声线树树形结构的构建，起到加速追踪声线束追踪的作用。

1.1 三棱柱空间剖分

三棱柱空间剖分是一种基于三角剖分方法[14]的空间剖分方法。对障碍物区域进行平面三角剖分后，依据障碍物的高度拉伸各三角形，形成不同高度的三棱柱空间体。

三棱柱空间剖分需要解决立面是否为障碍物表面和同一障碍物不同高度等问题。

立面是否为障碍物表面。对数据库中障碍物端角点排序并标记障碍物所有立面，查找立面两边顶端角点判断其是否为障碍物内部，在则确定虚拟立面。

同一障碍物不同高度。切分并对切分后障碍物进行微偏移处理，切割立面即为虚拟障碍物立面，计算中使其不具备声音传播媒介功能。

1.2 四面体空间剖分

采用的逐点插入法构建非约束Delaunay四面体网时。在非约束Delaunay四面体网构中插入障碍物约束（边和面），在影响区域二次剖分，形成约束Delaunay四面体网格。

Delaunnay四面体空间剖分应用于障碍物群场景时，因实际条件的特殊性，需要对五点共球、约束条件恢复等进行处理：

五点共球问题。三维障碍物群和声源点形成的凸壳中，约束条件是矩形或是长方体时，会出现五点共球的情况，使得最优剖分结果有多种。在Delaunnay四面体剖分过程中，会产生剖分不唯一的问题出现。在实际操作中，采用顺序编号法进行解决。

约束边恢复问题。在剖分过程中，障碍物也内部被剖分，需要进行约束条件恢复。研究采用数据库自动更新的方式，在剖分过程中动态匹配数据库中的相应约束情况，在程序中添加控制代码检测插入点，判断形成的剖分边界是否为约束条件，并进行恢复处理。

1.3 时空效率比较

基于两种不同剖分方法的声线束追踪法具有不同的时间空间效率，其时间代价分为接收点网格生成、声源点网格生成、剖分单元生成、路径生成和声衰减计算五个部分，对于数据存储，则对接收点网格、声源点网格、剖分结构体和衰减计算结果有空间要求。两种剖分方式下的追踪方法时间复杂度和数据空间使用情况如表1所示。

表1 时间复杂度和数据库空间使用

两种剖分方式的声线束追踪法，在同一条件下接收点和声源点网格划分相同，其时间复杂度和空间数据库使用情况相同，S-R声衰减计算部分其时间和空间存储数据也相同。对每一个接收点判断接收点是否在建筑物内时间复杂度为O(R×B)，需要3×R×64 bits空间。声源点网格生成时间复杂度正比于Link的数目，在数据库体现为三个double型坐标，和两个Node的编号（整型），即3×S×64+2×S×16空间。路径生成过程要循环声线束树形结构中所有的节点，当找到所有的有效路径后，S-R衰减对计算时间为O(S×R)，并需要S×R×16空间。

两种剖分方式基本剖分单元不同，结构体生成过程时间复杂度为空间剖分时间与模拟障碍物和声源点插入时间的总和，两种方法分别是O(2BPlogP)+O(BL)和O(3BPlogP)+O(BL)；三棱柱剖分中，空间存储P个点由2n-2-k个三角形组成，共有3n-3-k条边，数据库中需要占用2×O(P)×7×16+3×O(P)×6×16空间，相应的四面体空间则需要3×O(P)×7×64+9×O(P)×6×64。

基于三棱柱的剖分方式在时间和存储空间上优于基于四面体的空间剖分方式。其优势体现在剖分结构体生成部分。

2 声线束追踪和路径生成

2.1 声线束追踪

形成基本剖分结构体网后，声线束追踪法通过生成的剖分结构体网格进行传播和追踪，在声线束传播过程中，记录声线束传播约束条件的编号根据传播过程进行更新。

以二维声线束追踪为例，当声线束从一个三角形的边传入新的一个三角形，当前的声线束根据可到达区域边界剪裁；当遇到约束边时，声线束会被反射；当遇到角点时，产生衍射声束；声线束随着剖分结构附带“上层”基因并标识是否由衍射或反射产生。声线束开始于声源点所在的结构体，根据剖分结构体网的拓扑关系递归追踪。本文采用树形结构体表示和存储这个追踪过程。树形结构节点存储的数据包括：当前四面体编号、当前边编号、当前面编号、反射次数、声源点或虚声源点坐标和衍射点位置。图1表示了声线束追踪过程。

2.2 路径生成

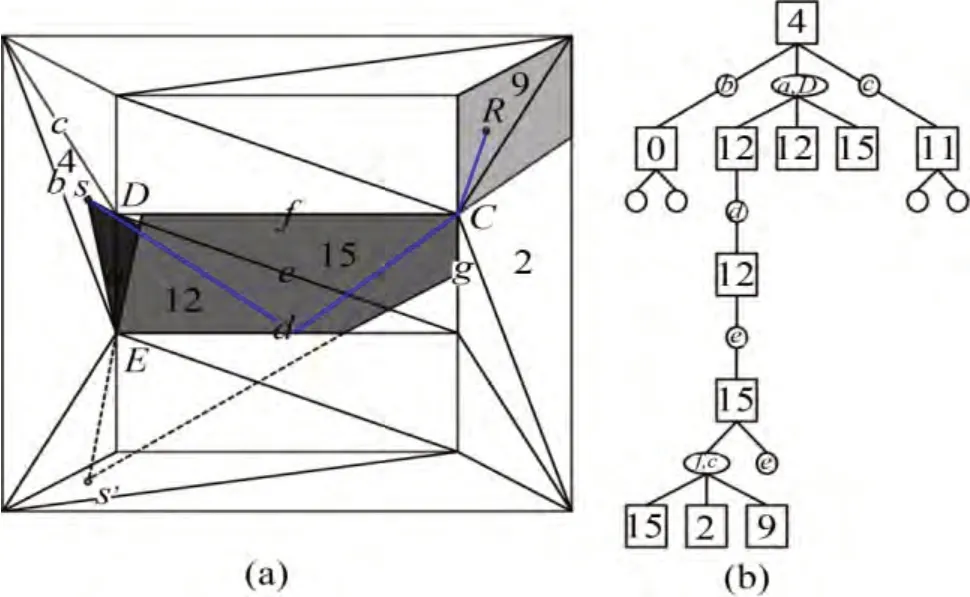
图1 基于空间剖分的声线束追踪法追踪

对于每一对接收点和声源点，它们之间可能有很多条路径，包括直射、反射、衍射和各种复合情况。所有路径可通过声线树形结构体快速找到。首先找出接受点所在的结构体。然后枚举树形结构体中所有的节点，找到符合追踪条件的目标节点直至追踪结束。在路径生成的过程中，需要对声线束追踪中经过的约束边或面以及影响四面体进行记录。当目标节点找到后，就能相应生成一条从声源点到接收点的三维有效路径。

在图1所示的例子中，可以找到从声源点S到接收点R的一条路径可以描述为

4(S)→a,D→12→d→12→e→15→f,C→9(R)

3 声音传播模型

声线束追踪法被用来快速生成由声音传播所有有效路径。对于任一接收点P，所有的有效路径中的声线可以分成4类：直射声线、反射声线、衍射声线和包含反射和衍射的复合声线。根据相关经验[15]，反射次数取2次。

在任一时间步长t，接收点P处的声强是所有这些路径的贡献总和，如公式

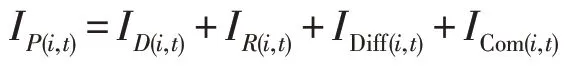
4 点声源声音传播实例

4.1 基本参数

实验选取广州大学城电信大楼和城管委员会大楼（27 m）区域，电信大楼呈L形，有三个不同高度（24 m、10 m、30 m）。的建筑物布局、实验监测点和声源点位置如图2所示。

实例计算过程设定表面反射系数设为0.8，反射最大次数为3次。声源为单点定频率声源，由发声装置发出，无声源指向性，在空旷空间7.5 m处测得声压级为79.5 dB，高度为0 m，频率为630 Hz。测得实验背景声为40 dB。

4.2 实例计算结果及效率分析

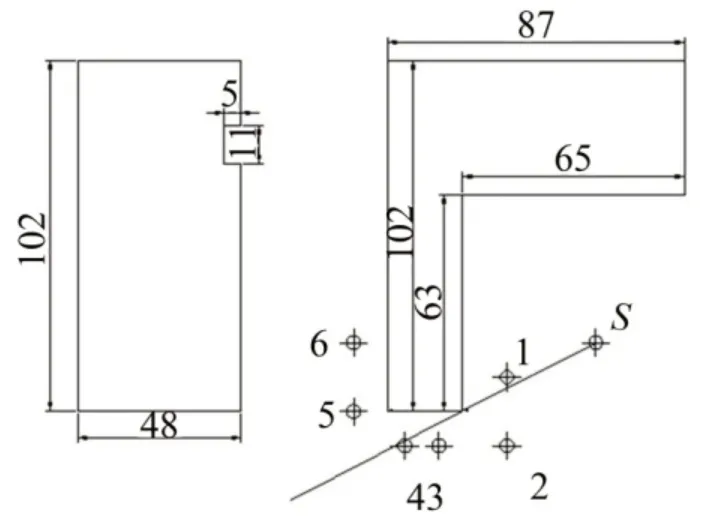
图2 障碍物示意图及点位信息（单位m）

算例得到了在典型区域内的单点声源声音传播分布，研究选取高度分别为1.2 m和3 m两个平面进行分析。图3为两种不同剖分形式下，该区域3 m高度水平面声场分布情况，两种方式下平均声强分别为67.3 dB、和65.6 dB。

计算过程中，基于不同剖分方式的两种方法的参数比较如表2所示。

从图3可以看出，点声源发出球面波系由一半径固定的脉动球产生，其衰减特性与接收点距离有关；声波传到第二媒介（障碍物）由分界处产生反射，附近区域声场由声源传来的直达声和来自虚声源的声迭加求出，声压级大于同距离下的只有直射区域；经过障碍物边界时，声波发生衍射，声压级由边界向内部递减，在障碍物背后的边缘附近生成声影区。计算数据表明，基于三棱柱剖分和四面体剖分的声线束追踪法均能对建筑物区域声衰减进行计算，并能很好的符合声音的衰减规律。

图3 三棱柱（上）和四面体（下）剖分下试验区域声场分布

由表2可知，基于三棱柱剖分的声线束追踪法在时间和空间效率上明显优于基于四面体的声线束追踪法。时间上，两种方法计算用时均远大于剖分用时，这是由于实例中障碍物和接收点数目比较少，剖分的方式比较简单，而四面体剖分方法剖分单元更细，剖分过程以及在剖分结构体中寻找路径是其耗时较多。存储空间上，四面体剖分具有更大数量的剖分单元体结构及可能路径，这使得其需要空间较三棱柱剖分多。

4.3 计算和实测数据比较

试验区域监测点在高度为1 m和3 m的计算和实测数据如表3、表4所示。

两种不同剖分方式下，声线束追踪法计算结果在1.2 m处的误差均值为1.22 dB和1.02 dB，而在3 m处，其误差均值为1.6 dB和1.31 dB。两种方法实测的6个数据点的误差绝对值不大于3 dB，且平均误差都控制在1～1.5 dB，两种方法均符合精度要求，在计算3维声传播问题时有良好的表现。

4.4 精度分析

两种计算方法和实测值在监测点在不同高度的数据对比趋势如图4和图5所示，图中基于三棱柱和四面体的声线束追踪两种方法分别用“方法一”和“方法二”表示。

图4和5显示两种方法误差均控制在3 dB以内，能很好的描述障碍物下的三维声场分布。距离声源点越近，其路径所经过的不必要的剖分单元越多，计算偏差越大，造成两种方法均呈现绝对误差随着接收点远离声源点而减少的趋势。

表2 不同方式剖分方法实例计算数据比较

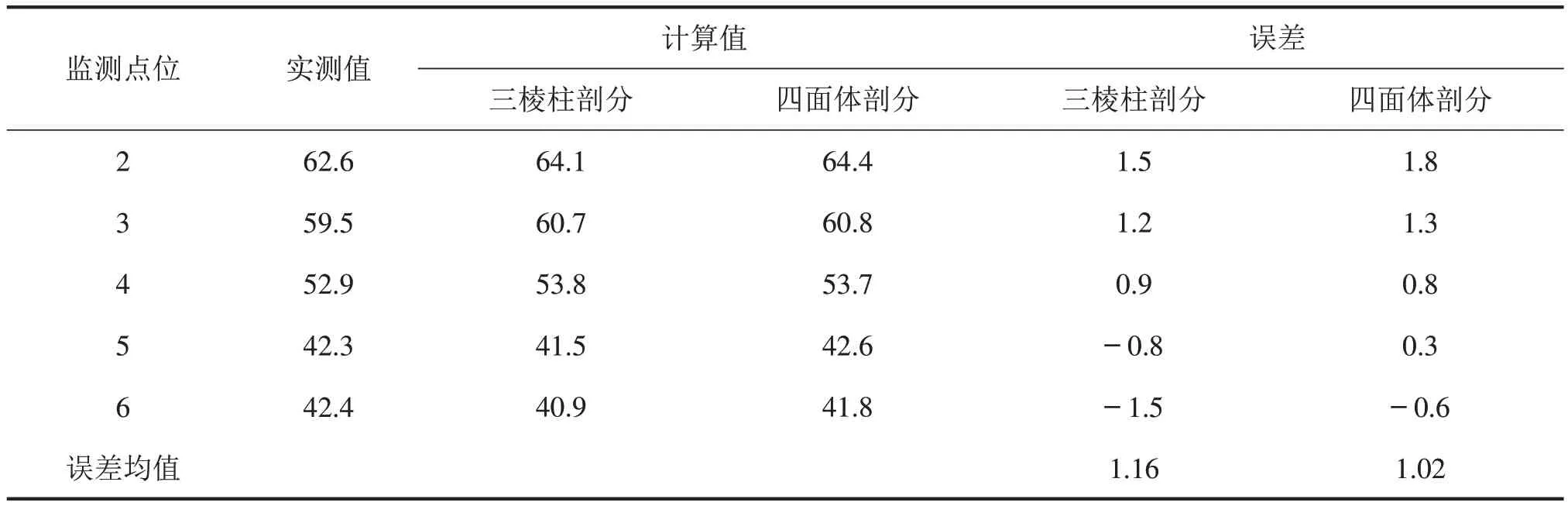
表3 实测和计算数据(H=1.2 m,单位：dB(A))

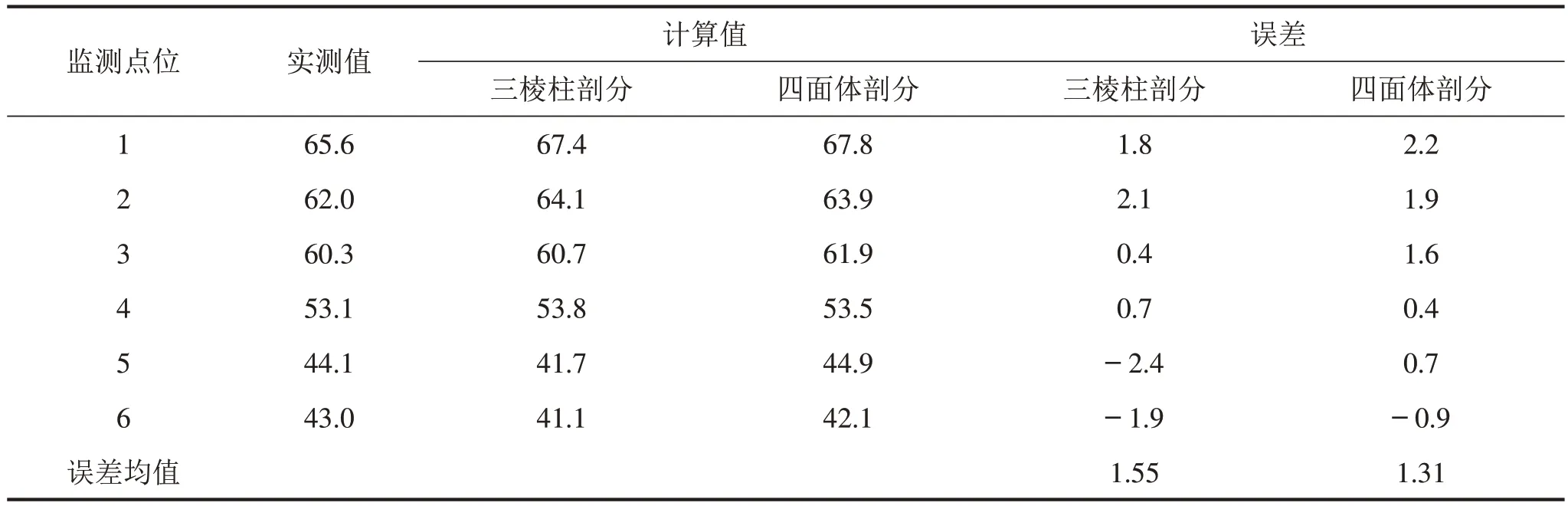
表4 实测和计算数据(H=3 m,单位：dB(A))

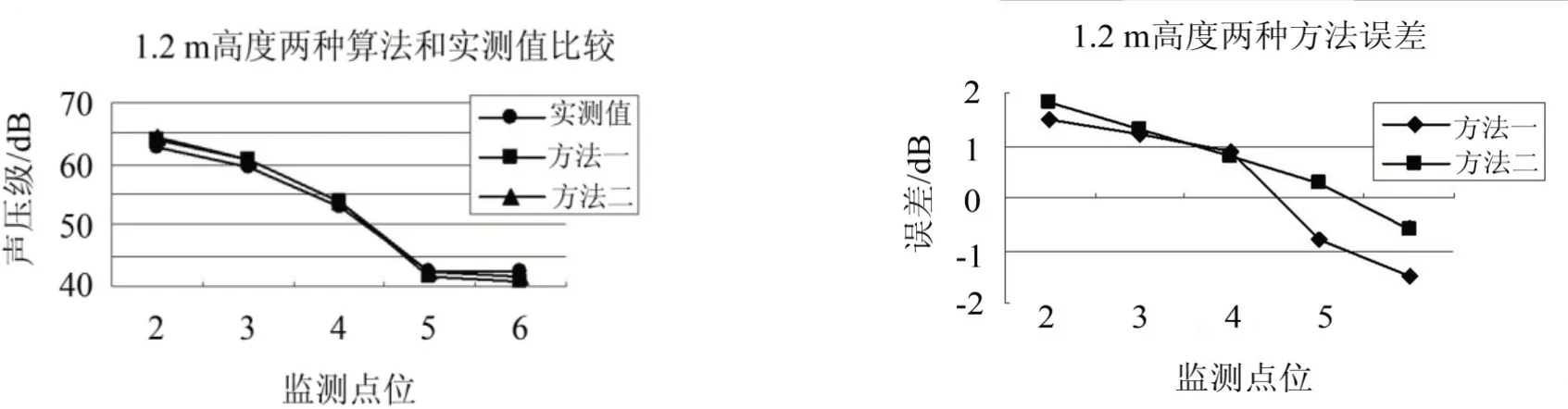
图4 实验区域1.2 m数据及误差对比

图5 试验区域3 m数据及误差对比

对于监测点1、2、3、4，在直射区和反射区，两种计算方法的误差在0.5 dB和2.5 dB之间，计算精度相当且计算结果都大于实测值，剖分结构的细化并没带来计算精度上的提高；所采用的恒定波束形成依赖于剖分结构，四面体结构的复杂性使得在处理简单问题的情况下比三棱柱结构有更多的误差积累，使得其误差反而较三棱柱剖分更大；对于监测点5、6，处于声衍射区，衍射路径包括顶端衍射和边角衍射，基于三棱柱剖分的声线束追踪法计算结果小于实测值，而基于四面体剖分的声线束追踪法计算结果则更接近实测值，其计算结果的精确性来源于剖分结构更细微合理，能更好的模拟声音在障碍物声影区细致的传播过程。

三棱柱剖分方式和四面体剖分方式1.2 m处计算值与测量值的标准差分别为1.22和1.09，3 m处的标准差为1.72和1.45。且四面体剖分方式下误差变动均为正值，其稳定性高于三棱柱剖分。

4.5 局限性分析

三棱柱剖分是基于三角剖分然后拉伸立面的剖分方法，在障碍物出现不规则形状（如顶端尖角等）时，剖分会遇到障碍，四面体剖分则解决了这一问题，满足声传播更为复杂的环境。两种方法均不能对弧形障碍物的声遮挡做出准确的计算。

5 结语

本文提出一种基于空间剖分的声线束追踪算法，该算法避免全局空间搜索，通过树形结构局部搜索并生成声线束路径，大大简化了算法的复杂性；另外，对比三棱柱和四面体两种剖分方式，其在时间、存储空间、精度和局限性上表现为：两种方法都能满足大区域声传播计算的精度，基于三棱柱剖分的声线追踪法具有明显的时间和存储空间优势，能精确的计算障碍物遮挡后声场分布，基于四面体剖分的声线束追踪法则在衍射区域计算、稳定性和适用性上优于前者。算法可应用与大区域声传播计算

[1]Drumm I A,Lam Y W.The adaptive beamtracing algorithm[J].Journal of the Acoustical Society of Ameerriiccaa,2000,107:1405-1412.

[2]Yang L N,B M Shield.Development of a ray tracing computer model for the prediction of the sound field in long enclosures[J].Journal of Sound and Vibration,,2000,229:133-146.

[3]Coensel B De,Muer T De,Yperman I,Botteldooren D.The influence of traffic flow dynamics on urban soundscapes[J].Applied Acousttiiccss,2005,66:175-194.

[4]Ismail M R,Oldham D J.A scale model investigation of sound reflection from building facades[J].Applied Acoustics,,2005,66:123-147.

[5]Hornikx M,Forssen J.The 2.5-dimensional equivalent sources method for directly exposed and shielded urban canyons[J].Journal of the Acoustical Society of America,2007,122:2532-2541.

[6]Pamanikabud P,Tansatcha M.Geoinformatic prediction of motorway noise on buildings in 3D GIS[J].Transportation Research Part D-Transport and Environment,2009,14:367-372.

[7]姜 薇,李太宝.三维声线追踪的正三棱锥前向伸展算法[J].声学学报，2005，30(5)：404-408.

[8]黄月琴，张建中.基于波前传播时间差值的三维声线追踪算法[J].声学学报，2008，33(1)：21-27.

[9]张胜勇，陈心昭.利用边界元法中的全特解场方法计算结构振动声辐射[J].噪声与振动控制，1997，12(6)：8-10.

[10]LUO W L,CAI M,FENG L I,LIU Ji-ke.Dynamic modeling of road traffic noise around building in an urban area[J].Noise Control Engineering Journal,2012,60(4):353-362.

[11]Miehael MurPhy,Mount David M,Gable Carl W.A pointplacement strategy for conforming delaunay tetrahedralization proceedings of the eleventh annual symposium on discrete algorithms[J].Association for Computing Machinery,2000,1:67-68.

[12]程承旗，郭 辉.基于剖分数据模型的影像信息表达研究[J].测绘通报，2009，10(2)：47-51.

[13]高珊珊，张彩明，周元峰，伯彭波.壳空间剖分的隐式曲面三角化[J].计算机研究与发展，2012，49(2)：432-442.

[14]Krockstadt U.R,Calculating the acoustical room response by the use of a ray tracing technique[j].Sound VViibb..,1968,8:118-125.

[15]Kang J.Urban sound environment[M].London and New York:Taylor ＆ Francis,2007.