动力传动系统扭转振动的分析及控制

任丽丽，施 善，刘友波

（北汽福田汽车股份有限公司 乘用车设计院，北京 102206）

近年来，随着生活水平的提高，选择车辆时，人们更注重车辆的各种性能，如NVH、操控性、舒适性等。目前，卡车、SUV等纵置后驱车型传动系统较长，易产生传动系统扭转共振问题，引起噪声、振动、耐久性等问题。产生共振时系统振幅较大，传递的扭矩增大，系统中承受大扭矩的部件很快被破坏。一般最先破坏的是油封，然后是齿轮轴承，最后是各种旋转部件。解决传动系统扭转振动问题是提高车辆舒适性、耐久性的一个关键项目，现阶段，大家越来越关注传动系统扭转振动问题。计算机仿真为预测和优化动力传动系统扭转振动问题提供一种有效的方法，这种方法还可以应用于汽车其它产品的开发、优化和验证。

1 理论知识介绍

1.1 基本公式

转动系统多自由度受迫振动的微分方程为

其中{θ}——角位移幅值列矢量；

[K]——扭转刚度矩阵；

[I]——转动惯量矩阵；

[C]——黏性阻尼矩阵；

{T}——激振力矩。

1.2 振动特性

系统振动由三个特性决定：自然频率、振型、频响，共振时通过调节这三个特性使系统得到改善。针对传动系统扭转振动问题对这三个特性分别进行描述：

（1）自然频率：传动系统的自然频率由各子系统的扭转刚度和转动惯量决定，它是系统的固有属性，自然频率个数和模型中自由度的数量相等；

（2）振型：描述系统在自然频率下如何振动以及相对振幅，每一阶自然频率都有不同的振型；

（3）频响：在激振力的作用下，各子系统的振幅分别是多少，与各子系统的扭转刚度、转动惯量，系统的约束方式、激振力、阻尼密切相关。

1.3 共振理论

任何部件和系统都有自然频率，动力传动系统也有自身的弯曲频率、扭转频率等，每个方向设计不好都可能引起严重的问题。传动系统扭转自然频率为fn，发动机的转速为nc，当发动机激振力某简谐分量的频率与传动系统固有频率接近时，就会发生共振，共振时转速nc称为临界转速，此时有

其中ν——发动机激振力简谐次数（四冲程发动机ν=0.5，1.0，1.5，2.0,……；二冲程发动机ν=1，2，3，4，……）[8]

图1中，f1、f2、f3、f4为传动系统前几阶自然频率，ν0.5、ν1.0、ν1.5、ν2.0……为发动机激振力前几阶简谐力矩。当曲线fn和vn相交时，发动机的简谐力矩击中传动系统的自然频率，产生共振，交点对应转速nc为临界转速。从图1看出，在发动机工作转速范围内遍布了各阶次临界转速，但这些临界转速对系统扭转振动造成危害的并不多。主要考虑这几方面：发动机常用工作转速、激振力矩的幅值、传动系统在某频率下的振型[1]。

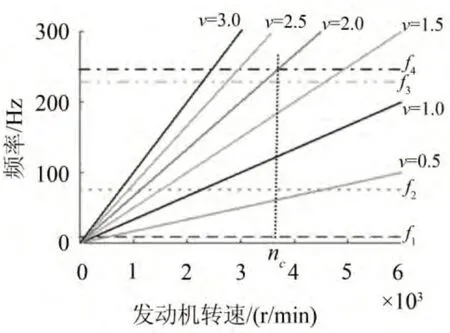
图1 临界转速示意图

2 无阻尼系统模态分析

这一部分主要讲述利用有限元软件建模、分析获得传动系统的自然频率，包含以下几点内容：简化模型、确定参数、自然频率和振型的解析。

2.1 简化模型

汽车动力传动系统是复杂的弹性体系统，构成系统的组件包括：发动机、飞轮、离合器、变速箱、分动器、传动轴、主减、半轴、轮胎等子系统，包括定轴转动、往复运动和平面运动[5]，在此采用集中参数模型对系统进行简化。简化模型由三种基本元素组成，集中惯量单元、无惯量阻尼单元、无惯量扭转弹簧单元，根据简化前后系统能量不变原则来建立传动系统的等效模型，把各子系统等效为集中惯量单元、弹簧单元、阻尼单元[9]。传动系统分析模型简化如图2，I i和K i所代表系统如表1。系统自然频率的个数由模型中自由度的数量决定，即为简化后子系统的数量。

图2 传动系统简化模型示意图

2.2 确定参数

求解系统自然频率要确定图2中所有集中惯量单元和弹簧单元的参数。有限元模型中只有一个转速，是以发动机转速为基准的。汽车运行时，从发动机传出的转速经过变速箱、主减后将发生改变，建模时根据能量守恒原则，对经过速比转换的部件进行转动惯量和扭转刚度的等效转换，每经过一个速比转换，后面部件的转动惯量和扭转刚度都除以速比的平方，表1为某车型3挡时各简化单元的参数。

2.3 自然频率及振型

轮胎和地面接触视为固定不动，通过分析得到系统自然频率、相对振幅和振型。自然频率不受阻尼影响，因此模型中没有考虑阻尼的作用。分析结果包含模型的特征值和特征向量，特征值的个数和模型中自由度的数量相等[10]。模型包含10个集中惯量单元，每个单元有一个转动自由度，分析结果得到10个自然频率，表2为系统自然频率和相对振幅。图3为前几阶相对振幅示意图，观察图3，可得到如下结论：

1阶自然频率振型：与X轴无交点，即所有部件都向同一个方向振动；

2阶自然频率振型：在飞轮和离合器之间与X轴有一个交点，即飞轮和离合器连接位置，传动系统扭转方向发生改变；

3阶自然频率振型：与X轴有两个交点，即传动系统的扭转方向发生两次改变。

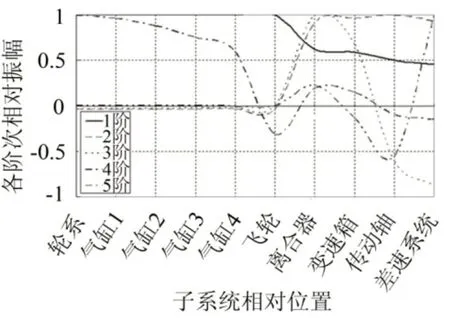
图3 无阻尼传动系统自然频率的相对振幅

3 频率响应分析

频响分析要考虑系统的激振力，系统的阻尼特性，在动力传动系统中这两部分都是比较复杂的参数[6]。

3.1 确定激振力矩

传动系统扭转振动的激振力主要是发动机产生的周期性力矩，由气缸内气体压力产生的力矩Tg和运动部件产生的惯性力矩Ti组成。如图4为试验测得发动机气缸压力图，可看出气体压力随转速变化不大。根据式（4）可知Tg随转速变化不大，根据式（5）可知Ti和转速的平方成正比，随着转速的不同，Ti变化较大。图5为发动机在2 400 r/min时单气缸压力及产生的扭矩。

气缸内气体压力产生的扭矩[3]

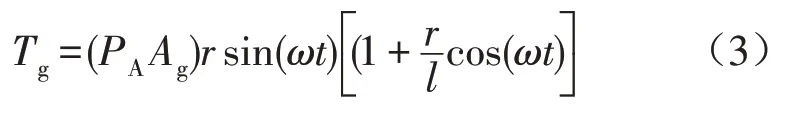
转动部件惯性力产生的扭矩

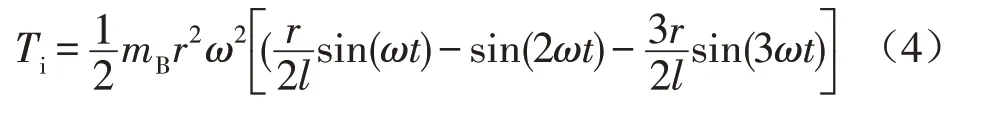
表1 传动系统各子系统参数

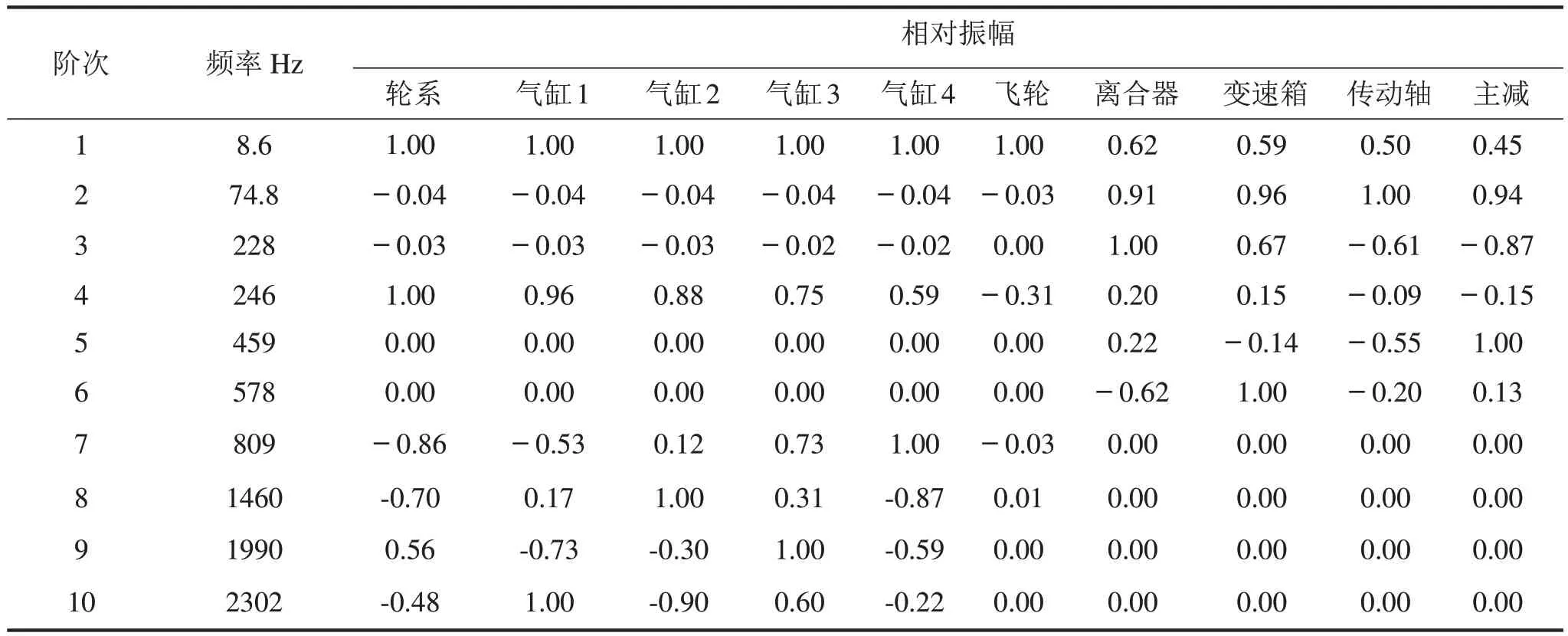
表2 无阻尼传动系统的自然频率及相对振幅

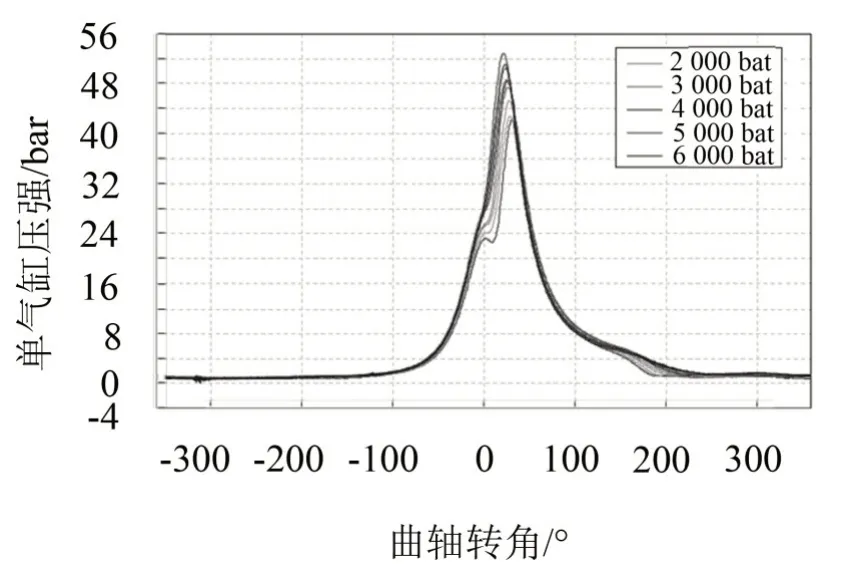
图4 单气缸压力测试曲线

发动机激振力矩

PA——单气缸气体压力；Ag——单气缸活塞面积；r——曲柄半径；l——连杆长度；Tg——气体压力产生的力矩；Ti——惯性力矩；Ttotal——单气缸激振力矩。

以2 400 r/min为例介绍发动机产生的激振力矩，把激振力矩转换为简谐力矩，图6为四冲程发动机单气缸激振力矩各简谐分量幅值随转速的变化曲线。在多气缸发动机中，只有具有较大幅值矢量和的简谐力矩才可能激起较大的振动，高阶次简谐力矩幅值较小可忽略。对四冲程发动机，当简谐次数ν等于q/2（q为气缸数）及其整数倍时，四个气缸简谐力矩的相位相同，表3为四冲程四气缸发动机各阶次简谐力矩相对相位角，此时发动机产生的简谐力矩幅值为单气缸力矩幅值的四倍，对应的简谐次数称为主简谐次数。主简谐力矩的幅值较大，共振时会激起系统的大振幅振动。

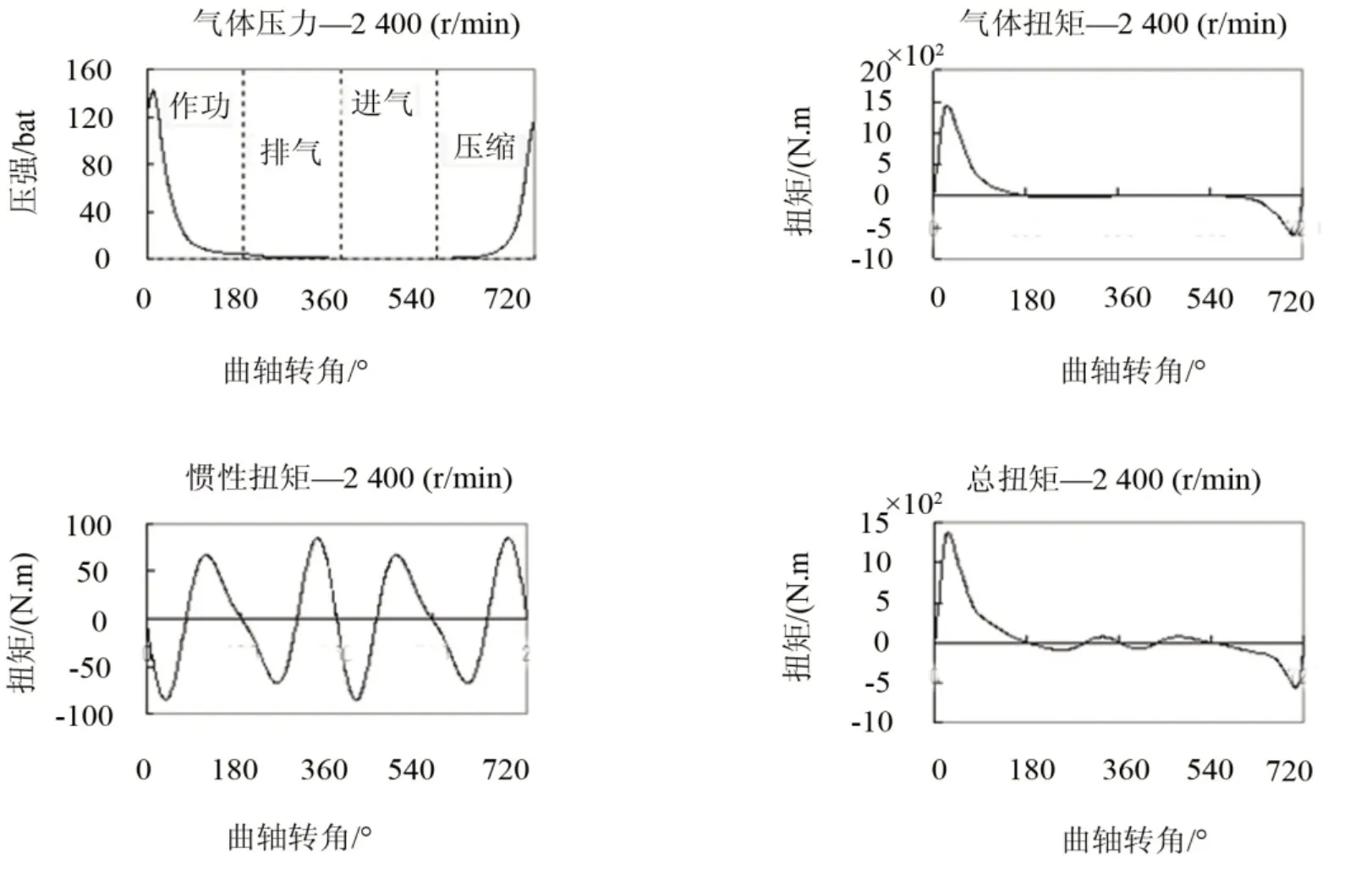
图5 转速2 400 r/min时，单气缸气压、力矩

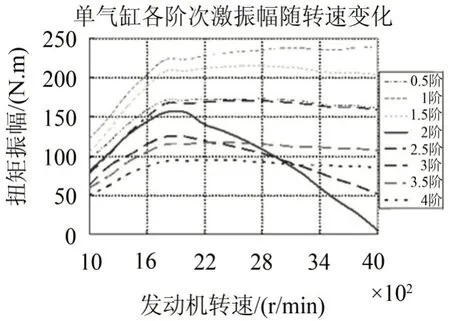
图6 单气缸简谐力矩幅值变化曲线

3.2 阻尼特征

常用阻尼有线性粘性阻尼和迟滞阻尼，这两种阻尼并不能概括实际系统中的所有阻尼，但线性粘性阻尼可以把复杂的非线性阻尼转换为数学上容易处理的阻尼。图7为两段式减振弹簧离合器的刚度与转角的关系，较小的直线斜率是用来控制怠速噪音的弹簧刚度，较大的直线斜率是用来控制扭转共振的弹簧刚度。平行线上下直线间的垂直距离的力矩值是来自摩擦的耗损扭矩，是设计值，和阻尼系数有关。

图7中离合器库仑阻尼计算公式为

线性黏性阻尼为

由式（6）、（7）得到

图7 离合器扭转刚度、阻尼特性

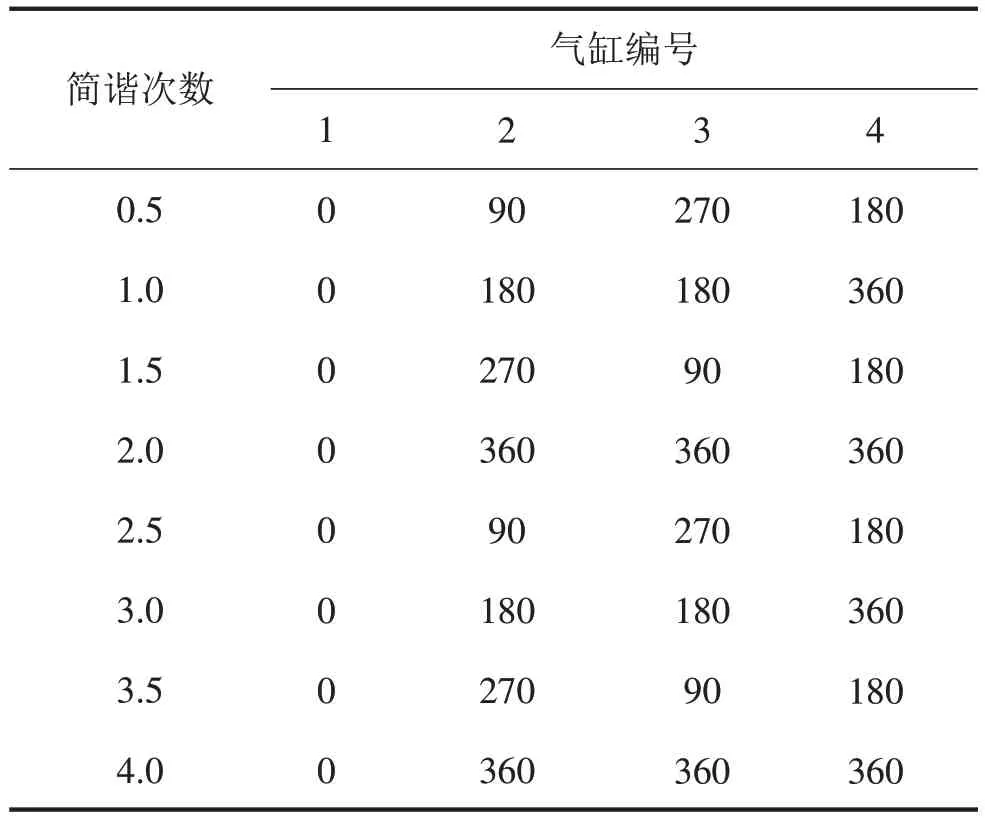
表3 四冲程四气缸发动机简谐力矩相位角 (单位：度)

式中Wc——阻尼功；C——等效黏性阻尼系数；TH——离合器来自摩擦的损耗扭矩；ω——传动系统扭转振动角频率；θ——离合器扭转角度。

在计算机仿真时θ随着输入参数C的变化而变化，根据式（8）可知θ的变化又会引起C的变化。因此频响分析时，需要根据初始条件先假设一个阻尼系数C1，进行分析，读出阻尼扭转角度θ1，再把θ1放到式（8）中计算，得出阻尼系数C2，如果C1和C2不相等，则要把阻尼系数C2放入模型重新计算，计算出阻尼扭转角度θ2，由θ2计算出C3，比较C2和C3.....经过这样不断的推算，直至Ci+1和Ci相等时，即得到合理的阻尼系数，把此值带入模型中分析频响[2]。

3.3 频响分析

图8为输入系统激振力的二阶简谐分量时，模型中各子系统的扭转振幅随简谐力矩频率的变化情况，从图8可看出，在激振力频率f=74.8 Hz时，击中传动系统2阶自然频率74.8 Hz，即发生共振，此时系统振幅即扭转角度θ增大。模型中弹簧的扭转刚度K是定值，根据T=Kθ可知，传递的扭矩增大。设计时，各部件都有最大允许承载扭矩，如果超过极限，部件就可能发生破坏或者降低使用寿命。由此可知，传动系统的扭转振动问题，不仅是噪声振动问题，也是可靠性耐久性问题。

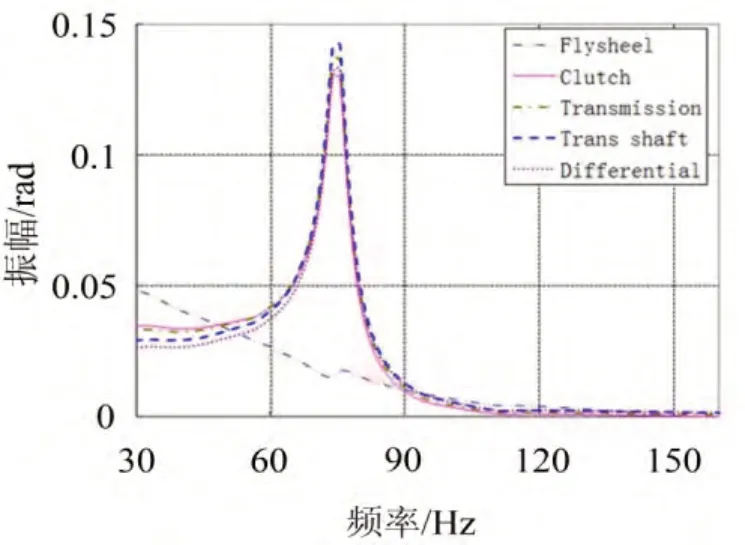
图8 频响结果—振幅和点火频率

4 解决方法

传动系统扭转共振中，振源是发动机的2阶激振力。发动机工作转速一般在600～6 000 r/min范围内，根据激振力矩2阶简谐分量的频率和发动机转速的关系[4]：f=2(n60)，对应频率为20～200 Hz，传动系统自然频率在此范围内的为74.8 Hz，对应发动机转速为2 244 r/min。即发动机在2 244 r/min时产生激振力矩的2阶简谐分量和动力传动系统2阶自然频率发生共振，从图8看出，此时离合器、飞轮、变速箱等系统的振幅很大，系统振动将比较剧烈、产生轰鸣声，某些部件传递的扭矩会增大，零部件的使用寿命降低。该如何解决这种问题呢？解决共振问题一般是从三个方面着手：振源、传递路径、振动体，根据发生共振时的不同部件、不同特点，要从不同的方面解决问题[10]。下面对传动系统扭转共振问题中的这三个因素分别进行分析。

4.1 振源

振源即激振力，改变激振力有两种方法，一是改变激振力频率，使激振力频率远离传动系统频率，汽车运行时发动机2 244 r/min的转速为最常用转速，不可能避开此频率。二是改变激振力的大小，即减小发动机传递的扭矩，这样即使点火频率和系统自然频率接近，但激振力比较小，将不会引起系统的大振幅振动。通过分析激振力的来源以及控制方法，了解到要改变振源需要对发动机的结构做较大改动。设计初期，发动机特性已经确定，发动机结构作较大改动对已经定型的发动机很难实现。因此解决动力传动系统的扭转共振问题时，一般不从振源着手。

4.2 传递体

发动机和外界接触主要有三个通道，悬置、离合器、发动机外壳。传动系统扭转共振问题中，传递通道为离合器，可以通过增大离合器中的阻尼阻碍激振力的输出。离合器中刚度和库仑阻尼是相关的，当离合器刚度降低时，阻尼将增大。

4.3 振动体

在传动系统扭转共振问题中传动系统为振动体，可以调节系统的自然频率，使系统自然频率对应的转速不在发动机常用转速范围之内。根据单自由度系统自然频率公式f=(1 2π)·k I有：系统自然频率与弹簧刚度成正比、与集中惯量单元转动惯量成反比，可以通过改变弹簧刚度和转动惯量来改变系统的自然频率。在传动系统共振问题中，一般降低系统自然频率来避开发动机常用转速，即降低弹簧刚度和增大转动惯量。不同振型的自然频率对各单元参数的敏感度也是不同的，一般节点附近刚度的变化、远离节点转动惯量的变化，对相应振型的频率影响较大，据此可以仅调整某阶固有频率而保持其它阶次基本不变。一般通过下面这几种方法来实现：降低离合器刚度、在传动轴上加小飞轮、使用双质量飞轮。下面是针对上面例子的3种优化方案和自然频率分析结果，如表4所示。

表4 优化方案及结果

由表4可知：每种优化方案都降低了系统的自然频率。方案1离合器刚度降低的同时会引起离合器阻尼的增加，有利于降低传动系统振幅，图9为原方案和方案1车辆行驶时车内噪声试验结果对比；方案2双质量飞轮降低系统频率效果最明显；方案3增加一个小飞轮，其它位置结构没有变化，操作方便。每种方案各有利弊，根据具体情况实施一种或几种优化方案。

5 结语

利用此项技术处理动力传动系统扭转共振问题，已得到具体车型的应用，在设计阶段解决了车辆存在的传动系统扭转共振问题，取得了成效。由于时间和试验设备有限，在后期将继续进行这方面的试验，让分析和试验更好的结合起来。

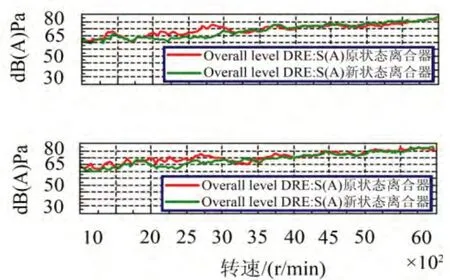
图9 不同离合器车内噪声试验结果对比

这种计算机仿真方法和处理此类问题的操作流程不仅用于解决动力传动系统扭转振动的问题，还可以进行多项产品开发和设计验证，针对汽车的设计开发，这项技术在下面这些开发验证中都可以得到很好的应用：

(1)设计阶段可用来鉴定减震器的设计是否合理；

(2)鉴定双质量飞轮的优势；

(3)检验发动机前面的阻尼设计是否合理；

(4)针对一些问题在传动轴上加阻尼设计；

(5)悬置的设计、开发、优化；

(6)悬架的设计、开发、优化。

[1]庞 剑，谌 刚，何 华.汽车噪声与振动—理论与应用[M].北京：北京理工大学出版社，2006.119-145.

[2]Christopher Keeney,Shan Shih.Prediction and control of heavy duty powertrain torsional vibration[A].SAE Paper 922481[C].International Truck and Bus Meeting and Exposition Toledo,Ohio November 16-19,1992.

[3]Robert L Norton.Design of machinery[M].McGraw Hill Higher Education,2007.521-561.

[4]Shan Shin,Jacinto Yruma,Phill Kittredge.Drivetrain noise and vibration troubleshooting[A].SAE Technical Paper 2809[C].2001.

[5]唐 斌，薛东新，宋希庚.复杂分支轴系扭转振动分析的研究进展[J].噪声与振动控制，2009，29(3)：1-5；58.

[6]梁兴雨，舒歌群，李东海，沈影刚.基于柔体曲轴多体动力学的轴系扭振响应分析[J].内燃机工程，2007，28(4)：46-49.

[7]毕金亮，李静波，李宏成，田 雄.动力传动系统扭转模态及灵敏度分析[J].振动工程学报，2010，12，23(6).

[8]黎 辉，周瑞平.柴油机轴系扭转振动简谐系数计算方法研究[J].江苏船舶，2007，24(2)：11-13.

[9]赵 骞，邓江华，王海洋.传动系部件扭转刚度对后驱传动系扭振模态的影响[J].噪声与振动控制，2011，11，31(5)：49-52.

[10]熊建强，黄菊花.混合动力汽车噪声和振动的分析与控制[J].噪声与振动控制，2009，11，29(5)：96-100.