基于LQG的穿浪双体船垂向运动控制系统设计

关 劲，宋 超，张松涛

(1．海军装备部，北京100841;2．哈尔滨工程大学，黑龙江 哈尔滨150001)

0 引 言

穿浪双体船(Wave Piercing Catamaran，WPC)最早由澳大利亚INCAT 公司提出，设计建造的“威尼斯王子”号横渡太平洋和印度洋，获得成功。其继承了小水线面双体船低阻、高耐波性及甲板面积宽敞等优点，克服了前者片体无储备浮力和复杂的航态控制、传动系统等缺点，同时吸收了深V 型船优良的航行性能［1］。WPC 以良好的总体性能，在高速车客渡船、军用高性能攻击舰和隐身舰等领域迅速扩展。

WPC 其独特的船体结构使得在横摇方面具有良好的耐波性，但在高海况高航速时，往往发生剧烈的纵摇和垂荡运动，出现砰击、甲板上浪等现象，并产生较大的垂向加速度，导致乘员晕船［2］，因此如何改善WPC 的垂向运动是姿态控制的研究重点。目前采用在船体上装备T 型水翼、纵倾调整尾板和船尾拦截器等一种或多种可控水翼，运用有效的策略对水翼进行控制，构成综合运动控制系统(Ride Control System，RCS)，利用其抑制船体的摇摆运动，改善船舶的耐波性、操纵性和舒适性，并减少能耗。这种技术在澳大利亚、美国等国家比较成熟［3］。

我国在装备多种可控水翼的运动姿态控制的研究相对较少，目前尚不具备独立设计能力，需要进一步探索。文献［4］以装备T 型水翼的86 m长的WPC 为研究对象，设计LQR 控制器，运用Fluent 仿真分析，实现垂向加速度减小24%，纵摇运动减少55%的效果;文献［5］研究安装T 型水翼的高速船，设计与110 m 实船比例为1/40 的自主动力船模，在露天水域进行实验，分析T 型水翼对垂荡、纵摇和横摇的影响及节能效果;文献［6］设计装备T 型水翼和尾板改进型快速船模，分析运用运动控制系统前后，海浪对模型耐波性的影响。以上文献研究的是只安装T 型水翼的作用或是多水翼对普通高速船的影响，没有关注多水翼的运动控制系统对WPC 垂向运动的改善情况。在此基础上，本文以装备T 型水翼和纵倾调整尾板的WPC 为对象，设计了运动控制系统，通过研究船体垂向运动的各项指标来分析所设计的控制系统的有效性。

1 模型分析

1.1 系统模型

由于WPC 的2 个船体形状相同，且对于纵中剖面对称，所以船的垂向运动(i=1，3，5)和横向运动之间无耦合［7］。本文主要针对WPC 的纵摇及垂荡运动进行研究，由此得到的带控制水翼的WPC 垂荡和纵摇耦合运动的方程组如下:

式中:下角标3和5 为垂荡和纵摇的相关参数;FT－foil和MT－foil为T 型水翼提供的垂向水动力和力矩;Fflap和Mflap为尾板提供的垂向水动力和力矩。

图1 WPC 运动控制系统Fig.1 Ride control system of WPC

其中的水动力系数是根据切片理论进行求解的。图1 为船舶运动控制系统框图。

根据式(1)，其相应的状态空间模型及其推导如下所示:

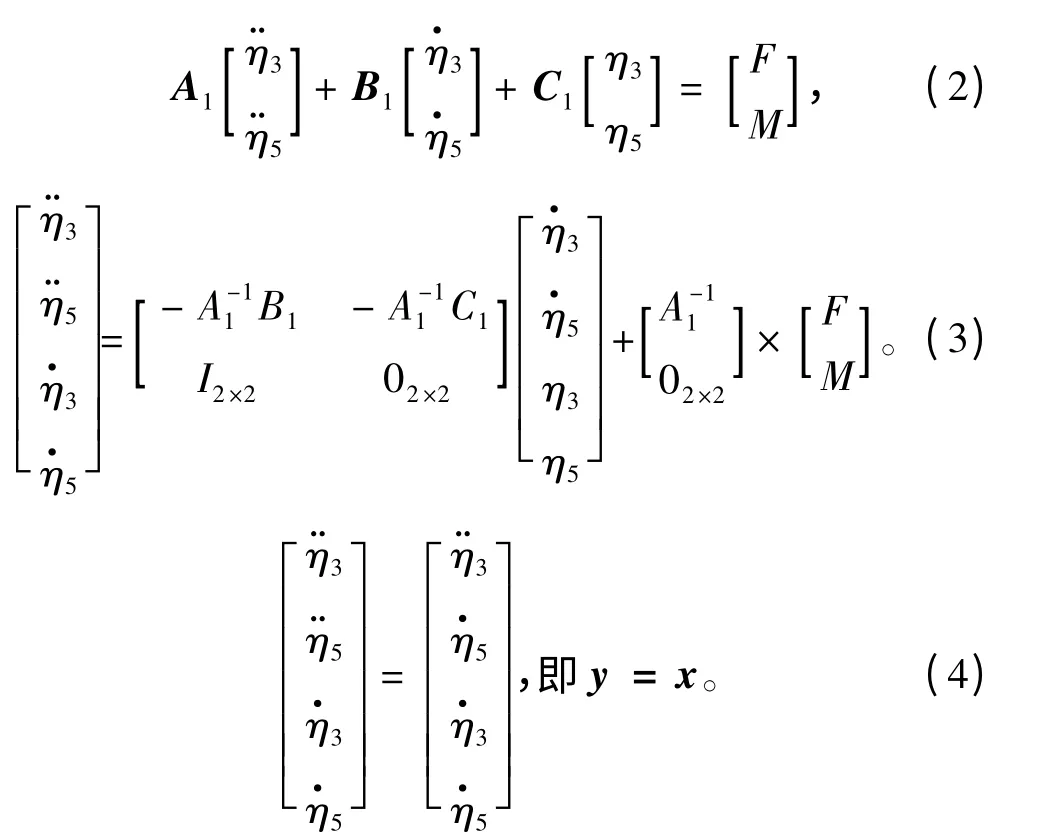
1.2 海浪干扰模型

在对船舶垂向运动仿真及船舶控制系统研究中，考虑波浪产生的随机干扰力和干扰力矩是非常重要的。为了研究方便，用于模拟的海浪状态模型是一个Pierson-Monskowitz 波谱［8］。定义式如下:

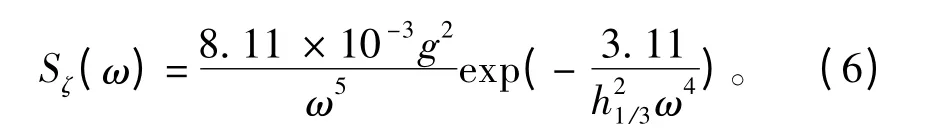
式中:S(ω)为波浪振幅谱，m2s;ω 为频率，rad/s;g 为重力加速度，m/s2;H13为海浪的有义波高，m。

利用波谱密度来描述不规则波浪，采用余弦序列权重系数法(见式(7))，来计算波浪作用于船体上的随机干扰力和力矩。

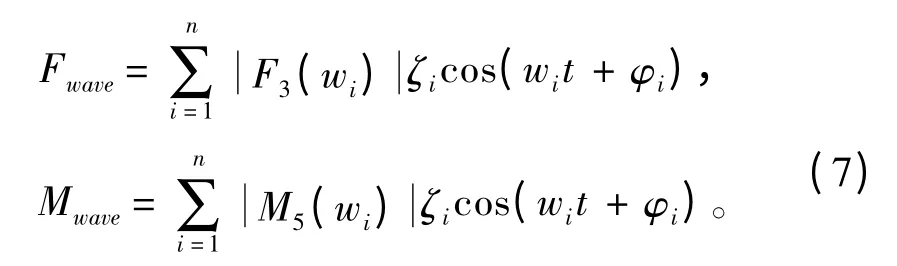
1.3 控制水翼水动力特性

在研究T 型水翼和尾板对减小船舶垂向运动的贡献时，先考虑升力的作用，然后通过以下分析得到纵摇和垂荡方向上的力和力矩。

1)T 型水翼

图2 为T 型水翼受力分析示意图。

图2 T 型水翼受力分析示意图Fig.2 Force analysis diagram of T-foil

T 型水翼上的升力计算模型［9］如下:

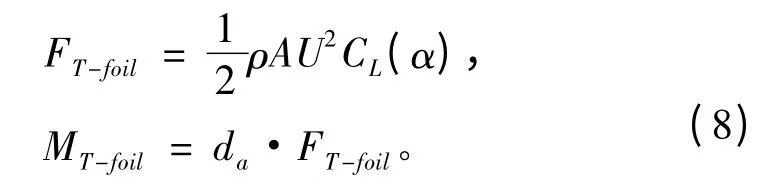
式中:ρ 为水密度，103kg/m3;A 为翼面积，m2;U为船速，kn;α 为翼面的有效攻角，(°)，有效范围为－15° ～15°;CL(α)为翼的升力系数，在α 很小的情况下可将其视为常量。

从实践的角度出发，在WPC 以航速40 kn 前行时，利用Fluent 软件进行水动力仿真确定翼升力系数，利用式(9)计算获得T 型翼在不同攻角下的升力系数CL(α)，然后通过拟合的方式获得升力系数满足的函数Y(x):

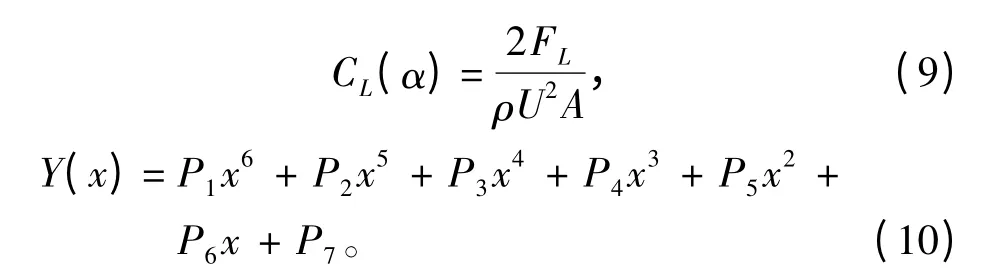
2)纵倾调整尾板

安装在船尾的尾板通过改变流过其表面的水流的方向产生作用力。如图3所示为尾板受力分析示意图。

尾板上的升力计算模型如下:

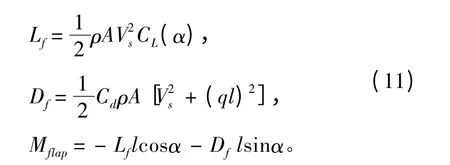
式中:Lf，Df分别为尾板上的升力和阻力，N;Cd为阻力系数;q 为纵摇角系数;l 为尾板的压力中心到纵摇轴的距离，m。

图3 尾板受力分析示意图Fig.3 Force analysis diagram of flap

2 LQG 控制器设计

由于控制器需要同时控制船的垂荡和纵摇，因此通过将上述2 个自由度设定成状态变量再根据最优控制去设计，这是一种即减小设计难度，又能观测每一个状态变量的实时变化的设计方法。

运用LQG 设计控制器可以满足运动控制系统的需要，根据分离原理首先得到的最优控制，它是最优滤波的线性函数，即

由于受控对象是线性定常系统，这里对其进行无限长时间的线性二次型最优状态控制器设计，定义其性能指标如下［9］:

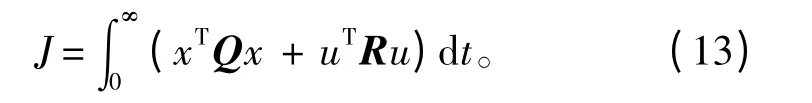
式中:Q 为常数对称正定矩阵，是状态加权矩阵;R为常数对称正定(或半正定)矩阵，是控制加权矩阵。仿真时比较关键的是加权矩阵Q和R 的选择，需要通过多组比较来确定。在此所取的LQR 权矩阵为:

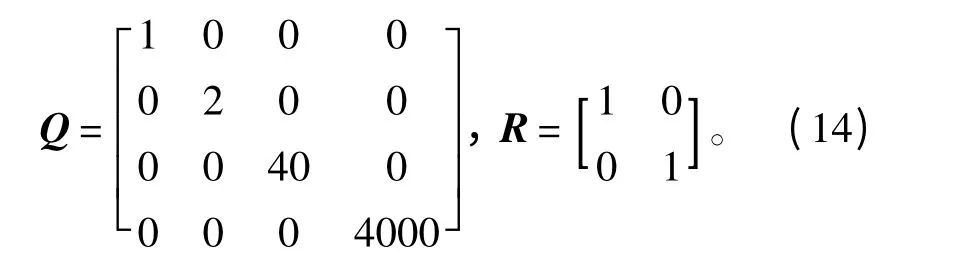
最优调节器的增益为:

最优控制为:

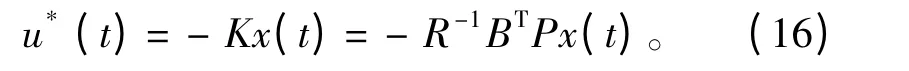
其中P 可通过Riccati 方程求出:

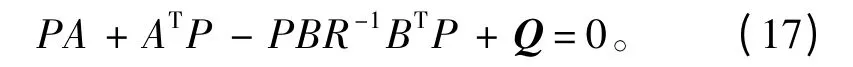
根据Kalman 滤波理论，最优估计^x(t)可从状态变量x(t)中得到，为估计误差，性能指标函数要求最优估计误差的平方取极小值:

式中:L 为滤波器增益矩阵，它的定义如下:

其中P0为以下Riccati 方程式的解:

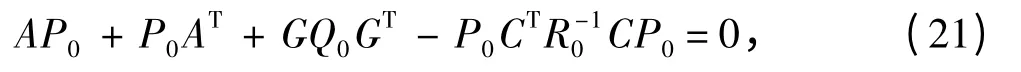
T 型水翼对应的的增益矩阵为:

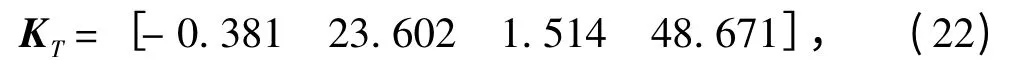
尾板对应的增益矩阵为:

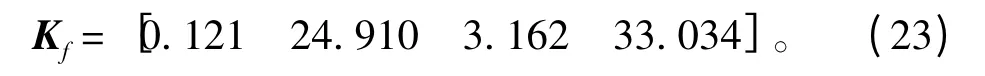
3 仿真实验研究

3.1 研究对象

用于研究的WPC 船型数据如下:船长L=90 m，排水量D=737.348 t，吃水T=2.6 m。当WPC 船速为40 kn，遭遇角为180°时，相应的状态空间系数如下:

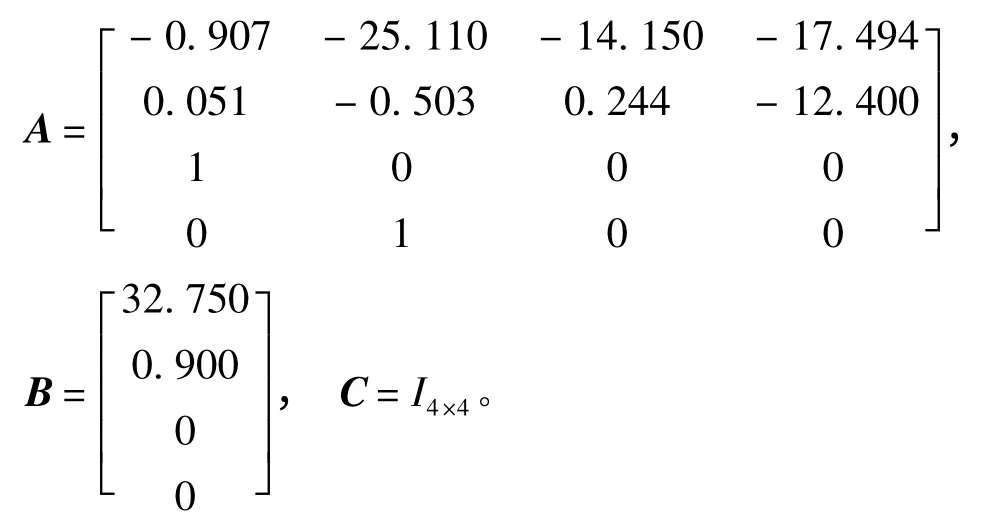
3.2 仿真实验

在船舶运动数学模型、海浪干扰力矩模型、T型水翼和尾板控制力和力矩的数学模型中，加入设计的线性高斯二次型最优控制器，然后利用仿真软件搭建仿真模块，对控制系统进行仿真，系统的总体仿真程序框图如图4所示。

LQG-flaps 模块为尾板的LQG 控制器，LQG-T-foil 模块为T 型水翼的LQG 控制器，Flaps model 模块为尾板的力和力矩，T-foil model 模块为T 型水翼的力和力矩模型。

3.3 结果分析

为了方便总结，将不同有义波高下的3 组仿真结果做一个对比，如表1所示。可以看出，在最常见的3 种海况下，采用LQG 控制的T 型水翼和尾板减摇效果明显，验证了控制器的设计合理，能够较好地减小垂荡和纵摇。

图4 WPC 运动控制系统仿真模块Fig.4 Simulation module of WPC ride control system

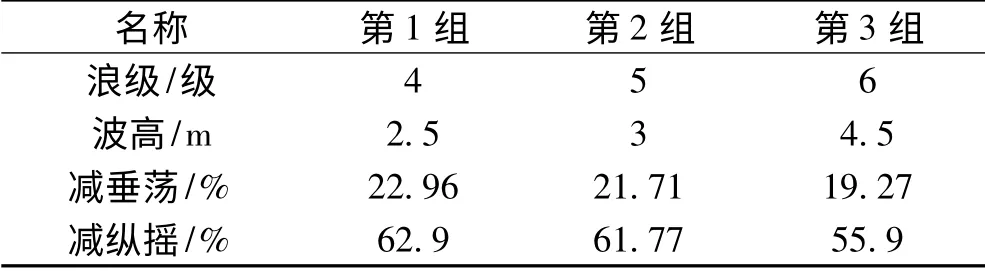
表1 不同海况下的减摇效果对比Tab.1 Comparison of stabilization effect in different sea state

图5 中仿真曲线表示的是第2 组:WPC 的航速为40 kn，遭遇角为180°，随机海浪有义波高2.5 m。为了显示方便，仿真图上的仿真时间为80 s。减摇仿真结果如下:垂荡减摇21.71%，纵摇减摇61.77%。

图5 垂向运动仿真曲线Fig.5 Simulation curves of vertical motion

4 结 语

1)分析T 型水翼和尾板的升力特性，仿真研究水翼和船体一起运动的情况。

2)设计LQG 控制器，实现2 种可控水翼的统筹配合。

3)T 型水翼和尾板构成的运动控制系统对穿浪双体船的垂荡和纵摇的改善情况。

4)通过研究分析船体垂向运动的各项指标验证运动控制系统的效果。

5)本文设计的双体船运动控制系统为广泛兴起的高速船垂向运动过大问题提供了借鉴方法。下一步将优化水翼参数，并探索运用到多水翼的高速船姿态运动控制系统中。

［1］夏齐强，陈志坚，孙春生．铝合金穿浪双体船波激振动响应计算研究［J］．舰船科学技术，2010(2):11－16．

XIA Qi-qiang，CHEN Zhi-jian，SUN Chun-sheng．A study on waveinduced vibration for aluminum alloy wave piercing catamarans［J］．Ship Science and Technology，2010(2):11－16．

［2］LIANG Li-hua，WANG Bao-hua，ZHANG Song-tao．Stabilizer fin effect on SWATH ship motions and disturbance observer based control design［C］．2013 10th IEEE International Conference on Mechatronics and Automation，Takamastu，Japan，2013:1147－1152．

［3］LIANG Liang，JIANG Jian-long，ZHANG Song-tao．Improving the vertical motion of wave piercing catamaran using T-foil［C］．2013 IEEE International Conference on Mechatronics and Automation，Takamastu，Japan，2013:1481－1485．

［4］ESTEBAN S，RECAS J，Giron-Sierra J M，et al．A fast autonomous scaled ship for experimental seakeeping control studies［C］．Oceans 2005－Europe．IEEE，2005(2):1232－1237．

［5］FALTINSEN O M，崔维成译．海上高速船水动力学［M］．北京:国防工业出版社，2007．

FALTINSEN O M．Hydrodynamic speed boat at sea［M］．Beijing:Defense Industry Press，2007．

［6］韩晓光，吴晞，郑环宇．波浪对穿浪双体船摇荡运动的影响［J］．舰船科学技术，2012，34(4):13－16．

HAN Xiao-guang，WU Xi，ZHENG Huan-yu．Research on wave-piercing catamaran features of swaying motions in the waves［J］．Ship Science and Technology，2012，34(4):13－16．

［7］解学书，钟宜生．H∞控制理论［M］．北京:清华大学出版社，1994．

XIE Xue-shu，ZHONG Yi-sheng．H∞control theory［M］．Beijing:Tsinghua University Press，1994．

［8］ZHANG Song-tao，LIANG Li-hua，WANG Jing-fu．Analysis of real time stabilization effect and parameter optimization of fin stabilizer［C］．2012 9th IEEE International Conference on Mechatronics and Automation，Chengdu，China，2012:1103－1108．

［9］FOSSEN T I．Handbook of marine craft hydrodynamics and motion control［M］．John Wiley ＆ Sons，2011．