两栖自行火炮水上横向射击稳定性仿真分析
蒋华剑,郭保全,孙明颜
(中北大学 机电工程学院,山西 太原030051)
0 引 言
两栖登陆作战是现代战争的一种重要作战形式。在登陆作战中,具备两栖作战能力的自行火炮已成为机动作战部队抢滩登陆的重要武器装备。两栖自行火炮进行水上射击时,车体在水中会产生6 个方向的摇荡运动。尤其是在水上横向射击时,产生的大幅度横摇运动对其稳定性威胁最大。从现有文献来看,马新谋、潘玉田等[1-2]对两栖武器在非射击状态下的线性与非线性横摇动力学做了较多研究,郭昭蔚、何安民等[3]对两栖武器水上纵向射击动力学做了一定研究,但是对横向射击稳定性的研究尚未得见。针对这一问题,本文利用Pro/Engineer和ABAQUS 建立了某两栖火炮的刚柔耦合多体发射动力学模型,并利用ADAMS 软件对其进行了横向射击动力学仿真分析,进而寻找出两栖自行火炮水上横向射击时的高低安全射角。
1 横向射击条件与基本假设
研究两栖自行火炮水上横向射击的发射动力学特性,需要给定一定的合理假设,以简化问题,提高计算效率。为此,本文给出以下射击条件与基本假设:
1)两栖自行火炮在无限广静水域中进行横向射击,不考虑波浪载荷和风速的影响;
2)两栖自行火炮的形状与质量左右对称;
3)只将身管作为柔性体考虑,其他部分认定为刚体;
4)不考虑炮弹弹带的挤进过程;
5)考虑弹丸与膛线身管的刚柔耦合接触/碰撞,考虑身管与摇架的刚柔接触/碰撞/滑移,考虑高低机主齿轮与摇架齿弧的接触/碰撞,考虑摇架耳轴与耳轴室的接触/碰撞。
2 刚柔耦合发射动力学仿真模型的建立
2.1 三维模型与全炮拓扑关系建立
三维实体建模,是多体动力学建模的基础。准确的三维模型能够保证对刚体接触判断与计算的准确性,同时也对柔体的模态计算、柔体间接触/碰撞的处理产生重要影响[4]。本文按某两栖轮式自行火炮机构运动特点,在Pro/Engineer 中进行三维建模,然后将模型后导入ADAMS/View 中(身管使用ABAQUS 划分网格后,通过MNF 中性文件导入),其水上横向射击仿真模型如图1所示。

图1 某两栖自行火炮水上横向射击动力学仿真模型Fig.1 Dynamics simulation model of an amphibious self-propelled gun when lateral firing on water
某两栖自行火炮简化模型全炮拓扑关系如图2所示。铰Hi(i=1,3,5,10,12,13,14)为接触副,铰Hj(j=4,6,7,9,11,15)为固定副,铰Hk(k=8)为滑移副,铰Hw(w=2)为旋转副。
为了方便模型的求解和仿真结果的分析,如图3所示,建立5 个参考坐标系:OXY 为惯性坐标系,O 点位于ADAMS/View 仿真平台的原点(0,0,0);O1X1Y1为车体坐标系,原点O1位于车体重心位置;O2X2Y2为后座部分坐标系,原点O2位于后座部分重心位置,X2轴与身管轴线平行;O3X3Y3为摇架坐标系,原点O3位于摇架左右两耳轴中心连线的中点;O4X4Y4为炮塔坐标系,原点O4位于炮塔重心位置。后4 个坐标系均与惯性坐标系平行。
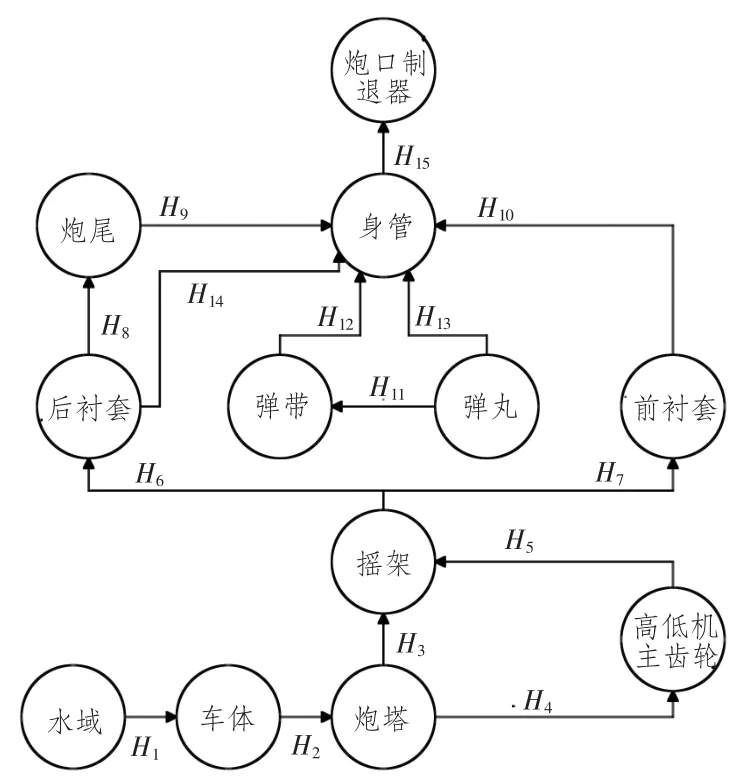
图2 某两栖自行火炮拓扑结构图Fig.2 Topological structure of an amphibious self-propelled gun

图3 某两栖自行火炮坐标系图Fig.3 Coordinates system diagram of an amphibious self-propelled gun
2.2 某两栖自行火炮水上射击载荷建模
某两栖自行火炮水上射击时的载荷分析如图4所示。
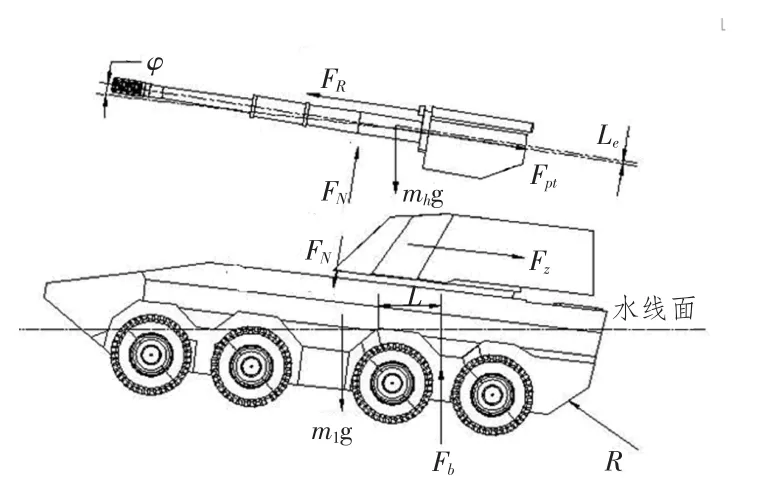
图4 某两栖火炮水上射击时的载荷分析Fig.4 Loads analysis of an amphibious self-propelled gun when firing on water
图中,φ 为火炮的高低射角;FR为后坐阻力,包括制退机液压阻力、复进机力、密封装置的摩擦阻力等;Fpt为炮膛合力,作用在炮膛轴线上;FN为摇架导轨提供的法向反力;mhg 为后坐部分的重力;Le为后坐部分质心到身管轴线的距离;m1g 为非后坐部分的重力;Fb为浮力;R 为水阻力;L 为浮力到全炮质心的距离。
1)炮膛合力的建模
火药气体对炮身的作用合力Fpt主要来自于膛底、坡膛以及气体流动对膛壁的摩擦力。气体与身管内膛壁的摩擦力与前两者相比,可以忽略。则Fpt的计算公式如下[5]:
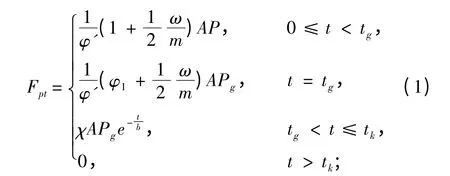
其中,
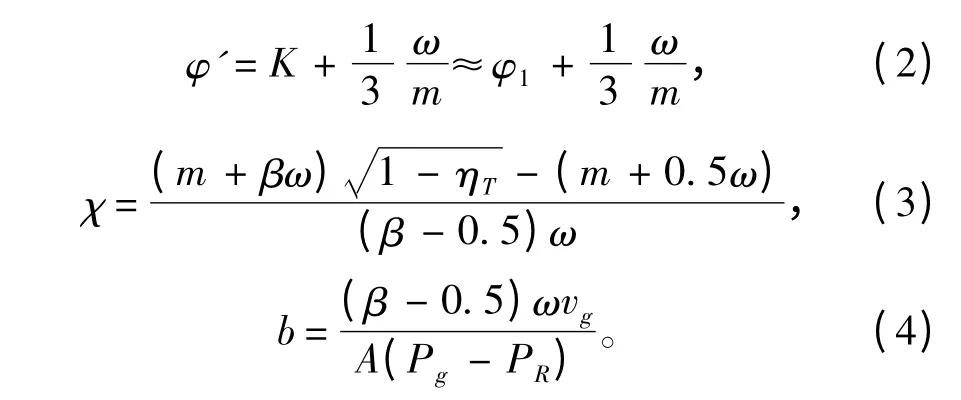
式中:φ′ 为次要功计算系数;φ1为仅考虑弹丸旋转和摩擦2 种次要功计算系数;m 为弹丸质量;ω 为装药质量;A 为炮膛横断面面积;P 为火药气体平均压力;Pg为弹丸出炮口瞬间的炮口压力;χ 为炮口制退器冲量特征值;b 为火药气体时间常数;tg,tk分别为弹丸出炮口和后效期结束时的时刻;ηT为炮口制退器的效率;β 为无炮口制退器时的火药气体作用系数;vg为弹丸出炮口瞬间的速度;PR为后效期结束时膛内火药气体平均压力。
2)后坐阻力的建模
后坐阻力方程为:
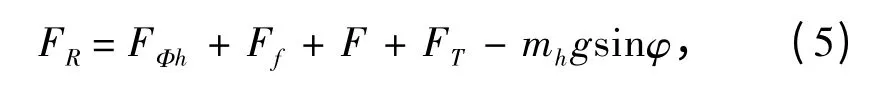
其中,


式中:FΦh为驻退机力;Ff为复进机力;F 为密封装置摩擦力;FT为摇架导轨上的摩擦力[5];mh为后坐部分质量;φ 为火炮射角;A0为驻退机活塞工作面积;AP为节制环孔的面积;Afj为复进节制器的工作面积;ax为节制杆任意截面对应的流液孔的面积;A1为支流最小截面的面积;K1为主流液阻力系数;K2为支流液阻力系数;ρl为液体的密度;v 为后坐速度;Af为复进机活塞工作面积;x 为后坐位移;Pf和Pf0分别为任一瞬时复进机中气体压力和气体初压;V和V0分别为任一瞬时复进机中气体的容积和气体的初始容积;n 一般取1.3;D 为相对运动表面的直径;d 为放置橡胶“O”型圈的矩形槽底的直径;p 为液体的压力;fc和fy分别为选用橡胶“O”型圈的摩擦系数和承压后橡胶“O”型圈附加的摩擦系数;μ 为摇架导轨的等效摩擦系数,取0.16 ~0.2。
3)浮力和浮力矩的建模
利用三维软件的二次开发,可获取车体在任意姿态、任意位置下浸入水中部分的体积[6],则由阿基米德原理可得浮力大小为:

式中:ρ 为水的密度;Vl为车体浸入水中体积。
调用三维软件中的质量特性工具,可以求出车体任意姿态、任意位置排开水的体积的几何中心相对于车体质心的坐标,也就是浮力的作用点,从而可以求出浮力到全炮质心的距离L,进而求出浮力矩:

4)水阻力和水阻力矩的建模
车体在水中受到的动阻力主要由摩擦阻力Rf和剩余阻力Rr两部分组成[7],即:

两栖自行火炮在水中所受摩擦阻力,相当平板的摩擦阻力与粗糙度增加的摩擦阻力之和。

式中:Rf为摩擦阻力;ΔCf为附加阻力系数;Cf为摩擦阻力系数;vl为车体在水中的速度;S 为车体浸入水中部分的表面积;Re 为雷诺数;L 为车辆水线长;υ 为运动粘性系数,当水温为12°时,取1.239×10-6m2·s-1。
剩余阻力为:

式中:ξ 为与车体外形系数;S1为车体浸入水中部分的最大横剖面积。
ξ和n 由某两栖自行火炮拖模实验结果拟合得出,最大横切剖面S1为车体浸入水中部分在其速度矢量vl方向的最大投影。
调用三维软件中的截面属性模块,计算出最大横切剖面相对于车体质心的坐标,进而求出阻力矩:

式中lR为投影截面形心到车体质心的距离。
3 刚柔耦合模型的水上横向射击动力学仿真计算
3.1 动力学数值仿真结果
在ADAMS 中,对前文所建立的两栖自行火炮模型进行横向射击仿真,车体在惯性坐标系OXY 下的运动结果如图5 ~图10所示。

图5 升沉位移Fig.5 Heave displacement

图6 横移位移Fig.6 Lateral displacement

图7 纵移位移Fig.7 Longitudinal displacement

图8 纵摇角Fig.8 Angle of pitching

图9 横摇角Fig.9 Angle of roll

图10 首摇角Fig.10 Angle of yaw
3.2 数据分析
1)车体的升沉位移随着射角的增大而增大;车体的横移位移随着射角的增大而减小,且数值总体较大,0°射角时甚至超过2.5 m;车体的纵移位移随着射角的增大而增大,但数值总体较小,最大不超过0.125 m。可见,后坐力在横向和竖直方向上的分力是车体在水中横移和升沉运动的主要因素。
2)车体的纵摇角随着射角的增加而增加。这是因为后坐阻力矩在纵摇方向上的分量与浮力矩之和是产生车体纵摇的主要因素,且2 个力矩方向相同。随着射角的增加,后坐阻力矩减少的程度要小于浮力矩增加的程度,即两力矩之和随着射角的增大而增大,故而引起纵摇角随之增大。
3)车体的横摇角和首摇角随着射角的增大而减小。当射角为70°时,横摇角为负值,说明车体左倾。这是因为随着射角的增大,使车体横摇的后坐力矩逐渐减小,当射角增大到一定角度后,作用在摇架上的后坐阻力逐渐偏向车体重心的左侧。
4)在0°射角时,车体的横摇角达到极限值,接近5°,对于某两栖自行火炮来说,比较危险;在射角为70°时,车体的升沉位移达到极限值0.46m,尚未超过车体的干舷。
可见,两栖自行火炮在静水中进行横向射击时,高低射角越小,其偏离航线和发生横向倾覆的可能性就越大;而在较大射角时,虽然升沉位移和纵摇角均有所增大,但是均在安全范围以内。所以,该两栖自行火炮在进行水上横向射击时,应尽量避免小射角射击。
4 结 语
本文以某两栖自行火炮水上横向射击稳定性为研究对象,首先在ADMAS/View 中建立了某两栖自行火炮的多体动力学模型,考虑了刚体间的接触/碰撞、柔体间的接触/碰撞和刚柔耦合接触/碰撞等复杂因素。并借鉴船舶理论,对两栖自行火炮车体在水中的水阻力和水阻力矩进行了建模。最后,通过对刚柔耦合模型的水上横向射击仿真结果进行分析,得出了两栖自行火炮在静水中横向射击时应尽量避免小射角,以提高横向射击稳定性的结论。
[1]马新谋,潘玉田,马昀.两栖作战武器线性横摇运动动力学分析[J].火炮发射与控制学报,2008(2):85-88.
MA Xin-mou,PAN Yu-tian,MA Yun.Linear roll motion dynamics analysis of amphibious combat weapon[J].Journal of Gun Launch & Control,2008(2):85-88.
[2]马新谋,潘玉田,常列珍,等.两栖作战武器非线性横摇动力学研究[J].火炮发射与控制学报,2010(4):66-69.
MA Xin-mou,PAN Yu-tian,CHANG Lie-zhen,et al.Study on nonlinear rolling motion dynamics of amphibious combat weapon[J].Journal of Gun Launch & Control,2010(4):66-69.
[3]郭昭蔚,何安民,刘海民,等.两栖装甲车辆水上射击位移规律仿真研究[J].计算机仿真,2013,30(1):54-58.
GUO Zhao-wei,HE An-min,LIU Hai-min,et al.Simulation research on displacement rule of amphibious armored vehicles shooting in water[J].Computer Simulation,2013,30(1):54-58.
[4]曾晋春.车载式火炮刚柔耦合发射动力学研究[D].南京:南京理工大学,2010.
ZENG Jin-chun.Study on the rigid-flexible couple launch dynamics of truck-mounted guns[D].Nanjing:Nanjing University of Science & Techndogy,2010.
[5]高跃飞.火炮反后坐装置设计[M].北京:国防工业出版社,2010.
GAO Yue-fei.Artillery recoil design[D].Beijing:National Defense Industry Press,2010.
[6]李美彦,郭保全,潘丹阳.基于Solidworks 二次开发的两栖武器浮心与浮态计算方法研究[J].火炮发射与控制学报,2010(3):5-8.
LI Mei-yan,GUO Bao-quan,PAN Dan-yang.Computational method on buoyancy center and floating state of amphibian weapons based on solidworks secondary development[J].Journal of Gun Launch & Control,2010(3):5-8.
[7]盛振邦.船舶原理[M].上海:上海交通大学出版社,2003.
SHENG Zhen-bang.Ship theory[M].Shanghai:Shanghai Jiaotong University Press,2003.

