Nash均衡模型的船舶主尺度多目标优选

林少芬，杨贵强

(集美大学 轮机工程学院，福建 厦门361021)

0 引 言

船舶主尺度优选方案中，必须全面考察船舶各项技术性能、经济性，注意主尺度的选择对技术、经济指标的影响程度［1］，多目标的船型优选属于非线性函数优化范畴。传统的多目标优化方法有梯度法、牛顿法和直接法等，这些方法继承了求解单目标问题的一些成熟算法和机理，但对于性质复杂不清的目标函数难以适用［2-3］。

在船型多目标优化过程中，设计者考虑多个性能技术指标，各目标之间相互冲突，难以找到一个最优的非劣解，只有综合考虑各目标函数的性质，才能得到最优均衡解。本文依据博弈理论，将运输成本TC和年运货量AC作为优化目标博弈方，运用非合作Nash 均衡博弈模型来平衡多目标之间的冲突和竞争，以Nash 均衡状态解作为最优解。

1 博弈论算法求解多目标优化

1.1 多目标优化问题的博弈描述

多目标优化问题是将n 个设计变量映射到m 个目标函数的向量函数，数学模型表示为:

式中:［x1，x2，…，xn］∈X 为设计变量;bi和ai为设计变量xi的上下限;p和q 分别为等式约束和不等式约束的个数。

将多目标问题转化为博弈策略问题，m 个设计目标看作是m 个博弈方，设计变量集X 视为博弈论中的策略空间S1，S2，…，Sm，多目标函数的约束视为博弈问题中的约束条件，通过某一方案优化后的结果可作为相应博弈方的得益。因此，式(1)中的多目标优化问题转化为对博弈问题G 的描述:

式中:u1，u2，…，um为m 个优化目标即博弈方，并满足:

1.2 Nash 均衡定义描述

1.3 基于Nash 均衡模型的求解步骤

求解步骤如下:

1)通过设计变量对博弈方得益的计算，得到隶属于各博弈方的策略集S1，S2，…，Sm;

2)在各博弈方策略集组合Si中随机生成初始可行策略组合为s0={s10，s20，…，sm0};

图1 Nash 均衡计算步骤Fig.1 Computing steps of nash equilibriu

1.4 博弈方策略空间计算

博弈理论分析多目标优化问题的关键技术在于将设计变量集X 分解为各博弈方拥有的策略空间S1，S2，…，Sm。本文通过计算设计变量对博弈方得益的影响因子指标，并对该指标进行模糊聚类，得到隶属于各博弈方的策略空间S1，S2，…，Sm。

计算步骤如下:

2)设计变量xj对第i 个博弈方ui的影响因子

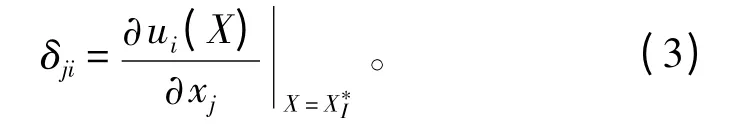
若无法通过目标函数偏倒计算影响因子，也可通过数值方式计算影响因子:在设计变量xj的可行空间中，按步长δj分为T 等段，则设计变量xj对第i个博弈方ui的影响因子:

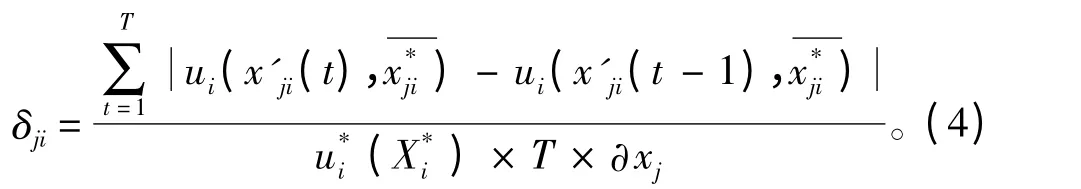
3)δj={∂ji，∂j2，…，∂jm}(j=1，2，…n)为分类样品表达式，δj为第j 个设计变量对所有m 个目标的影响因子集合。分类样品全体集合为∂={∂1，∂2，…，∂n}，对∂进行模糊聚类［8］，将设计变量集X 分解为各博弈方的策略空间S1，S2，…，Sm。

2 算例分析

利用文献［9-10］中的设计数据，本文考虑6个设计变量、2 个目标函数和11 个约束条件的多目标散货船船型优选问题。设计变量选定为船长L、船宽B、型深D、吃水T、方形系数CB及经济航速VK，设计变量集为x={L，B，D，T，CB，VK}T，计算模型见附录。

目标函数运输成本TC和年运货量AC作为博弈方，

式中:Whw为货物重量;RTPA 为每年周转次数;My为年费用。要求运输成本TC最小和年运货量AC最大。

约束条件选定:

25 000 ≤DWT ≤500 000;L/B ≥6;L/D ≤6;L/T ≤19;T ≤0.45DWT0.31;T ≤0.7D+0.7;0.63 ≤CB≤0.75;L ≤274.32;14 ≤VK≤18;Fn ≤0.32;GMT=KB+BMT- KG ≥0.07B。

式中:DWT 为载重量;Fn 为傅汝德数;GMT为初稳性高;KB 为浮心高;BMT为稳性半径;KG 为重心高度。

2.1 策略空间计算

1)采用序列二次规划(SQP)分别对目标函数TC和AC进行单目标优化，优化结果如表1所示。

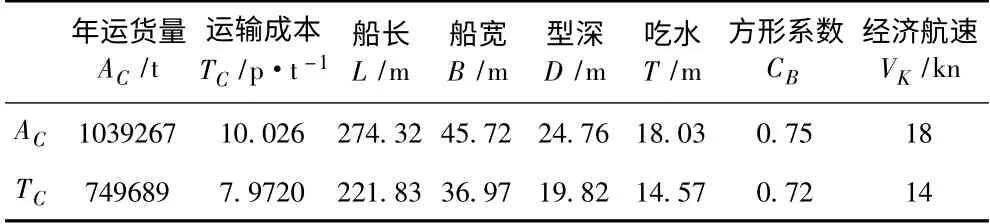
表1 单目标优化计算结果Tab.1 Computing results of single-objective optimization

2)根据式(3)，分别对目标函数求偏导，依据单目标优化结果计算影响因子:

δL={906.7551，0.0075};δB={6235.1，-0.0081};δD={-692.5211，-0.0748};δT={17492，-0.2089};δCB={376069，1.5098};δVK={12106，0.2020}。

3)模糊聚类分析

δ={δL，δB，δD，δT，δCB，δVK}={δ1，δ2，δ3，δ4，δ5，δ6}为影响因子全体，每个因子δi由一组数据{δi1，δi2}表征。建立δ 的模糊相似矩阵R=(rij)6×6，其中xi和xj的相似度 rij采用绝对值减数法 rij=计算［11］，则相似矩阵R 计算结果为:

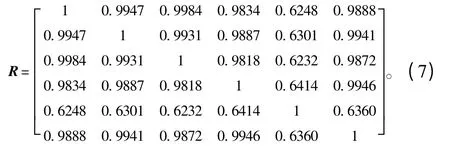
采用传递闭包法得:

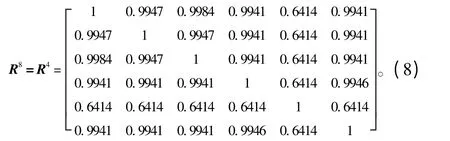
所以R4是R 的传递闭包t(R)。设为模糊等价矩阵，结合目标函数数量，取截值λ=0.9941，将δ 分成2 类:

经模糊聚类的结果得:博弈方年运货量AC的策略空间S1={L，B，D，T，VK}，博弈方运输成本TC的策略空间S2={CB}。

2.2 Nash 均衡计算

分别以策略空间S2的参数优选S1的5 个参数(即以运输成本TC的优选参数值CB作为年运货量AC优化的初始值)和以S1的参数优选S2的参数进行Nash 均衡求解，循环次数为200，得到200 个非劣解，TC和AC之间的非劣解的散点图分布如图2和图3所示。

将图2 中年运货量AC最大值用直线连接，根据运输成本TC由小到大得到5 个备选方案，具体参数见表2。图3 散点成线性分布，根据年运货量由大到小得到5 个备选方案(见表3)。

图2 非劣解散点图Fig.2 Scatter plot of non-inferior

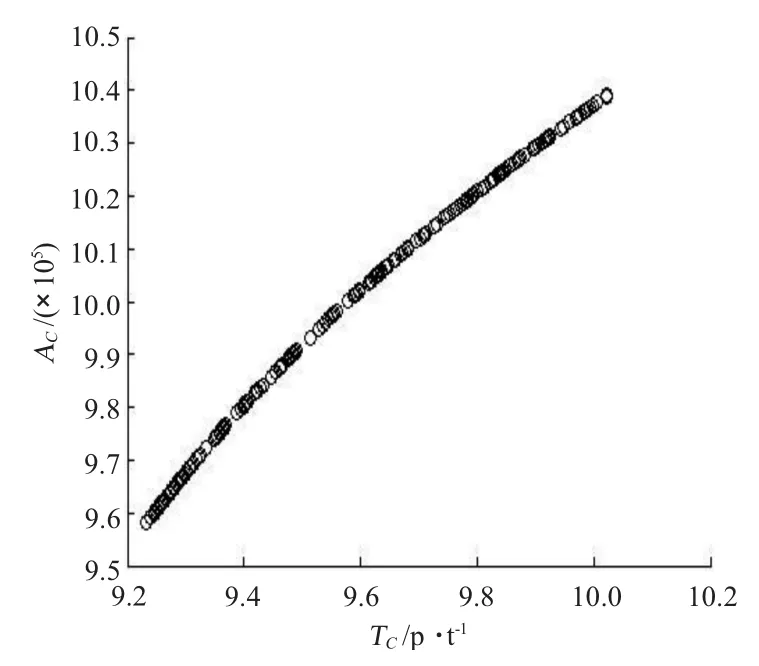
图3 非劣解散点图Fig.3 Scatter plot of non-inferior

表2 Nash 均衡博弈模型优化结果Tab.2 Optimization solutions of nash equilibrium model

表3 Nash 均衡博弈模型优化结果Tab.3 Optimization solutions of nash equilibrium model

从多目标优化问题定义讲，图2和图3 中的解都能作为式(1)的可行解，不同的优选方案得到不同的理想解。图2 优选结果明显优于图3，图2 中方案A(即表2 中方案1 的优选参数)为得益最佳的优选方案，满足运输成本T 最小和年运量AC最大。通过与文献［2］的比较，应用Nash 均衡策略求解多目标问题非劣解，可操作性强，较Pareto 解集更易控制。

非合作Nash 均衡博弈指各博弈方以竞争方式，并以自身的最佳得益为决策目标，其博弈结果可能对其他博弈方不利。通过计算策略空间的Nash 均衡解较优，但不能使各博弈方和整体性达到最优。

3 结 语

本文以散货船的年运货量、运输成本为主要目标进行了主尺度方案的优选。通过对比结果可知，Nash均衡博弈法能够快速、有效地选择船舶主尺度，对于不同的设计要求，能使各目标函数以自身的得益最大为目标，获得各目标函数之间的最优均衡解。在船型方案的优选中，为设计者提供更多的选择方案。

［1］顾敏童.船舶设计原理［M］.上海:上海交通大学出版社，2001.

［2］潘治，李学斌.改进的多目标优化算法及其在船舶设计中的应用［J］.中国造船，2010，51(2).

［3］李文龙，谭家华.集装箱船主尺度全局最优化的混沌算法［J］.中国造船，2003(1).

［4］张宏波，顾镭，徐有忠.基于博弈论的汽车耐撞性多目标优化设计［J］.汽车工程，2008，30(7):553-556.

［5］徐立哲，岑豫皖，谢能刚，等.基于Nash 均衡博弈模型的铣削参数多目标优化设计［J］.装备制造技术，2009(9).

［6］陈忠，谢能刚，张子明.结构多目标优化设计的合作博弈解法［J］.工程力学，2009，26(4):32-36.

［7］杨二波，陈明.船舶主尺度方案的博弈优选［J］.中国舰船研究，2010，5(6).

［8］XIE Neng-gang，SHI Na，BAO Jia-han.Analysis and application of multi-object decision design based on game theory［C］.6th World Congresses of Structural and Multidisciplinary Optimization.Rio de Janeiro Brazil，2005.

［9］SEN P，YANG J B.Multiple criteria decision support in engineering design［M］.Spinger，London，1988.

［10］PARSON M G，SCOTT R L.Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods［J］.Journal of Ship Research，2004，48(1):61-76.

［11］张弢，纪德云.模糊聚类分析法［J］.沈阳大学学报，2000，12(2):73-79.