时间模糊开关控制的自旋系统Lyapunov控制
(杭州电子科技大学,浙江 杭州310018)
0 引 言
近年来,量子计算的研究越来越广泛[1]。结合量子计算与模糊规则,对量子不确定性的研究构成了量子控制研究的一个新的分支[2]。量子力学主要考虑在n维希尔伯特空间中特定领域内的粒子,而模糊规则主要处理Rn空间特定子空间的一系列变量[3]。因此,可以考虑应用模糊规则与模糊计算来进一步研究量子计算。量子计算的模糊控制具有类似Bang-bang控制的开关特性,所涉及的问题将不包括量子计算机的物理实现问题。对量子计算的兴趣主要集中在机器学习的角度而不是物理角度。在物理学上关于量子力学特有的一些性质在本文中暂先不以考虑,考虑的自旋粒子不是选择性地可激发的。本文从控制理论的角度出发讨论了自旋1/2系统的模糊控制问题。通过量子态的轨迹误差分析和量子克隆,得到的量子态信息反馈到被控量子系统中。反馈控制的目的是让量子态从给定初态到达目标态。
1 问题的提出
主要研究自旋1/2系统的状态控制问题,描述系统的方程为薛定谔方程:
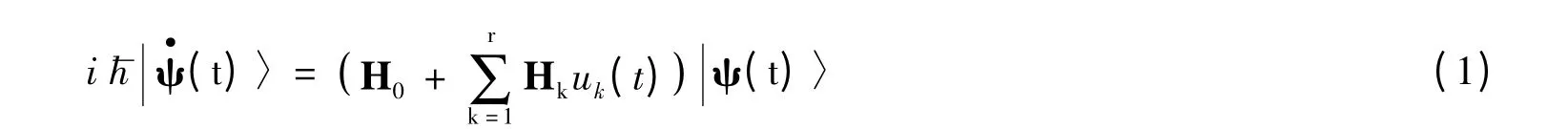
3)如果在当前时刻sgn(ekek-1)的符号改变,则在下一时刻应减少控制差Δu。
研究目标为对一个自旋1/2系统,找到一个模糊开关控制器,使得该纯态量子系统从一个给定初态到达目标态。
2 控制器设计
对一个自旋1/2系统的控制可通过改变其所在空间的电磁场在x轴,y轴和z轴的强度来实现。本文所设计的控制律保持或改变当前的控制行为可以通过增加或减少该时刻电磁场的强度来实现。如果把可行的控制域构成的闭包划分成n个模糊子集U(i),其相对应的隶属度函数之和1。当前时刻电磁场的增加或减少表现为控制u 应遵守以下n-1条模糊规则:IF U(k)is U(1)THEN U(k+1)is U(2);IF U(k)is U(2)THEN U(k+1)is U(3);……;IF U(k)is U(n-1)THEN U(k+1)is U(n)或者IF U(k)is U(2)THEN U(k+1)is U(1);IF U(k)is U(3)THEN U(k+1)is U(2);……;IF U(k)is U(n)THEN U(k+1)is U(n-1)。当sgn(ek-1)<0,sgn(ek)>0 或sgn(ek-1)>0,sgn(ek)<0时,由零点定理可知控制u(*)在区间[u(k-1),u(k)]内,此时对[u(k-1),u(k)]做n 等分,相应的划分小区间用U(1),U(2),…,U(n)表示。为满足以上分析的条件1 ~3,在第k步选取控制律u(k)满足:

其中开关增益λ 随着不同的分析结果做适当调整。量子测量可使被测对象以概率ci向其特征态塌缩[4],量子测量对被测对象的影响和破坏是研究量子控制的一个瓶颈。采用量子克隆的思想,在对自旋1/2系统的量子态进行控制后,把控制后的量子态进行复制并测量,再与目标态进行比较。总体的控制算法为:
2)通过IF-THEN 规则,利用模糊开关控制式对所研究的自旋1/2系统的量子态进行控制;
在实际操纵中,量子系统中存在着不可避免的不确定性因素,而这些不确定的因素无法通过一些常规的控制算法来解决,如最优控制,反馈控制等。近年来,越来越多的研究致力于通过模糊控制算法对量子系统的量子态进行控制,将模糊控制应用与量子系统控制可以在一定程度上有效地解决量子系统控制中由不确定因素引起的问题[4-6]。本文的创新之处在于在总结前人工作的基础上,对自旋1/2系统提出了一个具体特殊的模糊开关控制算法。
3 数值实例
考虑仅有一个控制作用的自旋1/2系统,设控制作用u(t)仅在y轴方向上改变电磁场,且选取自旋为σz表象,于是系统的薛定谔方程为:


本文对量子系统的控制可以看作一组离散事件,由式(2)可知第k步所选取的控制u1k满足即其中Δu为±λ 或λ 由IF-THEN 规则1 ~6 决定。将控制集合U 划分为n个控制子集U(1),U(2),…,U(n)。当Δu为正时,在下一微小的时间段内增大控制集的下指标;当Δu为负时,在下一微小的时间段内减少控制集的下指标;当Δu为零时,选取下一微小的时间段内保持当前的控制行为。对每步控制后的量子态进行量子克隆,再对克隆得到的量子态进行复制。
4 结束语
本文主要研究了在Lyapunov 稳定性理论下构造纯态量子系统的观测算子以提高量子状态演化的速度,所需解决的问题是一个最优化问题。研究发现系统在改进后的Bang-bang控制下所需的状态演化时间有所减少。此外,所提及的Bang-bang控制在实验仿真时具有较强的可操作性。对量子系统的控制是一组离散事件,相关思想可推广到对量子混合态的控制中。
[1]丛爽.量子力学系统的控制导论[M].北京:科学出版社,2006:67-73.
[2]陈宗海,董道毅,张陈斌.量子控制导论[M].合肥:中国科学技术大学出版社,2005:86-92.
[3]周世勋,陈灏.量子力学教程(第二版)[M].北京:高等教育出版社,2009:170-174.
[4]Rigato G G,Tzafestas S G.Parallelization of a Fuzzy Control Algorithm Using Quantum Computation[J].IEEE Transactions on Fuzzy Systems,2002,10(4):451-460.
[5]Chen C L,Dong D Y,Lam J,et al.Control Design on Uncertain Quantum Systems With Fuzzy Estimators[J].IEEE Transactions on Fuzzy Systems,2012,20(5):820-831.
[6]Li H X,Liu Z.A Probabilistic Neural-Fuzzy Learning System for Stochastic Modeling[J].IEEE Transactions on Fuzzy Systems,2008,16(4):898-908.
[7]Zhang X X,Li H X,Qi C K.Spatially Constrained Fuzzy-Clustering-Based Sensor Placement for Spatiotemporal Fuzzy-Control System[J].IEEE Transactions on Fuzzy Systems,2010,18(5):946-957.

