含区间右端线性规划的弱最优性

(杭州电子科技大学理学院，浙江 杭州310018)

0 引 言

在实际问题中，线性规划问题中的系数一般是不确定的，可转化为区间线性规划问题来研究。如何确定区间线性规划问题的弱可行解是否为弱最优解，在理论上和实践上都有十分重要的意义，文献[1-5]都对该问题进行了研究。本文主要讨论区间右端值线性规划的一般约束问题，并得出了检验其弱可行解是否为弱最优解的充要条件。

1 准备知识

本文将m×n 实矩阵全体表示为Rm×n，将m×n 区间矩阵的全体表示为IRm×n。设m×n 实矩阵A，m×n 区间矩阵其中m 维实向量和区间向量可以分别看作m×1实矩阵和m×1 区间矩阵[5]。考虑区间线性规划问题:

式中，A∈IRm×n，b∈IRm，c∈IRn且c是区间行向量。

令A∈A，b∈b，c∈c，则线性规划问题为:

称线性规划式(2)是区间线性规划式(1)的一种情况。

为了方便下面的讨论，给出弱可行解和弱最优解的定义。

定义1 若存在A∈A，b∈b，使得向量x 满足线性规划式(2)的约束条件，则称x是区间线性规划式(1)的弱可行解。

定义2 若存在A∈A，b∈b，c∈c，使得向量x是线性规划式(2)的最优解，则称x是区间线性规划式(1)的弱最优解。

引入区间右端线性规划问题的一般约束形式为:

式中，Aij∈Rmi×nj是mi×nj矩阵，bi∈IRmi是mi维区间列向量，cj∈Rnj是nj维行向量，xj∈Rnj是nj维列向量，i=1，2，3;j=1，2 且m1+m2+m3=m，n1+n2=n。

2 主要结论

将线性规划的KT条件推广到一般约束形式的线性规划，得到下述弱最优解判定方法。

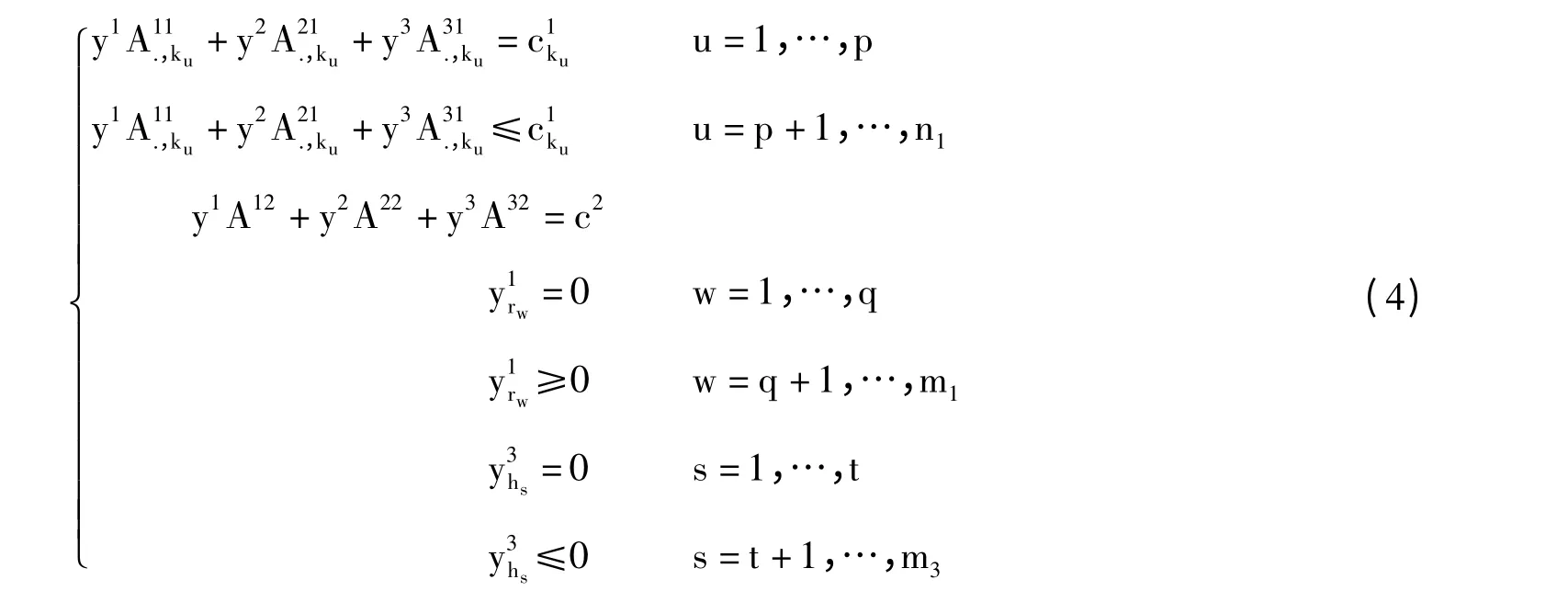
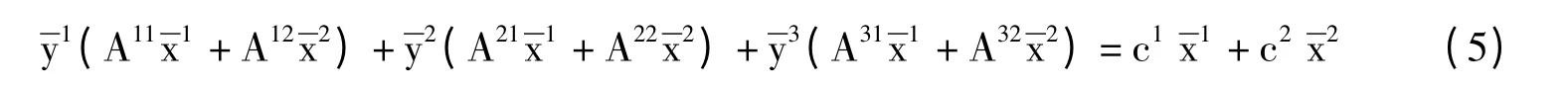
情况1 集合F1，F2都为空集。

1)当F1=φ时，令则是的解;

3)当F2=φ时，令则是的解;

情况2 集合F1为非空集合，F2为空集。

F2=φ 已在情况1 中讨论。下面讨论F1≠φ，令则b1。当k∈F1时，当k∉F1时所以是右式的解:由情况1 分析知，可找到满足一般约束形式线性规划的KT条件，并证得)即为式(3)的一个弱最优解。

情况3 集合F1为空集，F2为非空集合。

F1=φ 已在情况1 中讨论，F2≠φ时，与情况2 中对F1≠φ的讨论类似，不再详述。情况4 集合F1，F2都非空。

此情形是第2、第3种情况的两种子情况，综合可得到结果，不再详述。

因为式(4)是线性的，这种判定弱最优解的方法是多项式时间算法，非常具有可行性。

3 结束语

本文通过求解一个线性系统，给出了区间右端值线性规划的一般约束形式的可行解的弱最优性的判定方法。在研究区间右端规划解的弱最优性问题时，都可转化成这种约束形式利用上述定理来求解。然而，怎样去判定更一般的区间线性规划的弱解是否为最优解，目前还是一个比较困难的问题。

[1]Gabrel V，Murat C，Remli N.Linear programming with interval right hand side[J].International Transactions in Operational Research，2010，17(3):397-408.

[2]Li W，Luo J，Wang Q，et al.Checking weak optimality of the solution to linear programming with interval right-hand side[J].Optimization Letters，2013:1-13.

[3]李炜.线性优化及其扩展[M].北京:国防工业出版社，2011:200-232.

[4]Hladik M.Optimal value range in interval linear programming[J]，Fuzzy Optimization and Decision Making.2009，(8):283-294.

[5]Fiedler M，Nedoma J，Ramik J，et al.Linear optimization problems with inexact data[M]，New York:Springer，2006:35-92.