质量相关的故障诊断方法进展与展望

文成林，胡 静，李 平

(1.杭州电子科技大学自动化学院，浙江 杭州310018;2.浙江大学信息与电子工程系，浙江 杭州310027)

0 引 言

质量已成为21世纪的主题[1]。质量监测主要研究如何利用对生产过程内在变化轨迹的分析，进行产品质量的异常判断和实时预测，从而为提高产品质量提供有用信息。常见的质量监测方法主要有基于解析模型的方法和统计回归方法。基于解析模型的方法由于要求对过程工艺有充分的了解，因此在无法或难以获得精确数学模型的复杂工业过程中，其实际应用范围和效果受到限制。以多元线性回归(Multivariate Linear Regression，MLR)、主元分析(Principal Component Analysis，PCA)和偏最小二乘(Partial Least Square，PLS)等为核心的统计回归方法，因其只需正常工况下的数据来建立模型，且在处理高维、高度相关数据时具有独特的优势，而越来越受到研究人员和工程师的高度关注。

Pearson 于1901年最早提出PCA的概念，它通过建立数目较小的潜变量来更集中地反映原来变量中所包含的变化信息，有效剔除数据冗余[2-4]，并已广泛地应用于复杂工业过程的过程监控中。基于PCA的故障诊断方法将子空间中的所有变化都当作过程故障，而实际中人们往往最关心过程质量变量的变化，因此只对那些能够导致质量变量发生变化的故障感兴趣。PLS 就是利用质量变量来引导过程变量样本空间的分解，所得到的投影空间只反映过程变量中与质量变量相关的变化，因此具有比PCA 更强的对质量变量的解释能力[5-8]。PLS是MLR算法的一种扩展算法，它可以很好地解决许多以往回归方法解决不了的问题，比如过程变量之间的多重相关性问题和样本点不宜太少的问题，并增强了过程变量和质量变量之间的相关联度。特别是当质量变量之间存在较高程度的相关性时，用PLS 方法进行建模分析乃至故障诊断，要比对逐个质量变量作多元回归更加有效，其结论也更加可靠。

早在1966年，Wold 就提出了PLS算法并用于一块或多块数据的回归分析和建模，随后PLS 及其扩展方法在社会经济、化学计量学、化工过程等多个领域得到了广泛的应用，成为目前主要的成分提取和质量监测方法。国内外各科研小组均已投入大量的人力和物力，开展基于PLS的质量监测研究，取得了丰富的研究成果。本文将以PLS为主线，总结和梳理质量相关的故障诊断方法，及其在最近几年的研究热点、发展态势和展望，从而为后续研究理清思路。

1 偏最小二乘(PLS)

工业过程中存在着大量高度相关的过程变量和质量变量，过程变量(如温度、压力、流量等)通常都是按照秒或分的间隔来进行采样，而一些产品质量指标或与物料、能耗密切相关的某些关键过程变量(如磨矿过程的磨矿粒度和磨机负荷等)依然是离线测量的。产品质量指标主要采用人工定时采样、实验室检测等方法，可能需要数小时或数天的时间;某些关键过程变量主要依靠专家经验判断，依赖性大且稳定性差。质量变量通常会受到过程条件的影响，而这些过程条件会通过测量变量反映出来，为了更有效地监测工业过程的运行情况，同时利用过程变量的历史测量数据和质量变量的历史测量数据建立PLS 回归模型成为解决此问题的有力工具。

传统PLS 方法的目标是已知过程观测矩阵X∈RN×n和质量观测阵Y∈RN×m(直接或间接代表产品性能好坏)，寻找X数据空间中的低维潜变量t1，t2，…，tA(其中A ＜n为PLS 主元个数)[2]，对与Y 相关性强的部分进行描述，即:

式中，TPT表示与Y 相关的部分，E表示与Y 无关的部分，且满足统计无关条件E{TTE}=0。

由于PLS 方法刻画了过程观测阵X与质量观测阵Y的潜在线性关系，即:

因此，上述分解问题式(1)可转化为:

式中，Q=QuB=[b1qu1，b2qu2，…，bAquA]=diag{q1，q2，…，qA}。

PLS 方法求解潜变量ti的每一步都是一个寻优的过程，目标函数为:

传统PLS 方法中存在如下关系[9]:

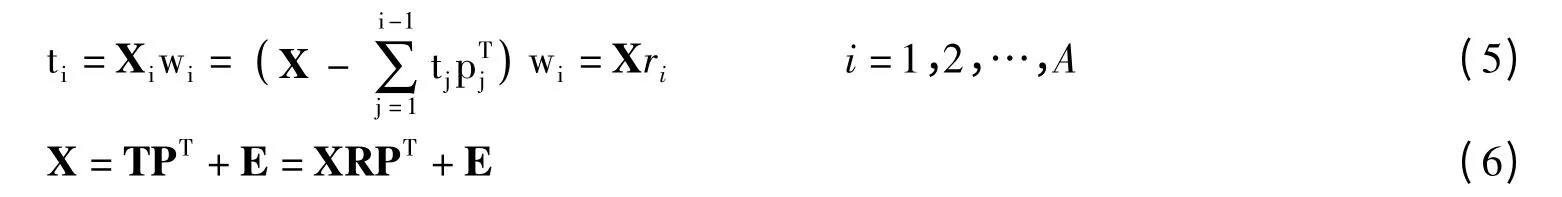
表1 传统PLS算法

文献[10]揭示了PLS模型对过程变量空间分解的几何特性。与PCA所建立的正交投影框架不同的是，PLS 诱导出了一个斜交投影结构:

其中，

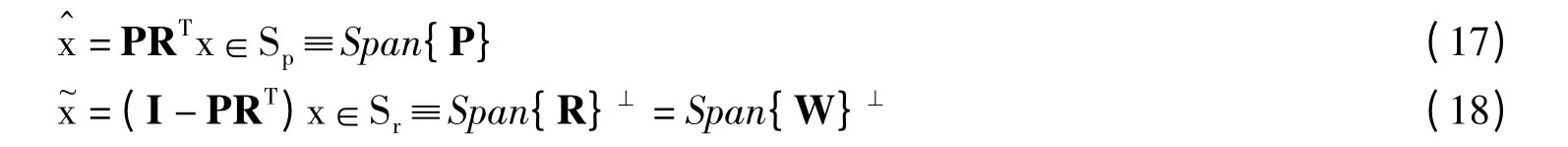
若改变式(19)为:

则对X数据空间进行分解后有:

利用性质WTW=I，并结合式(4)可得:

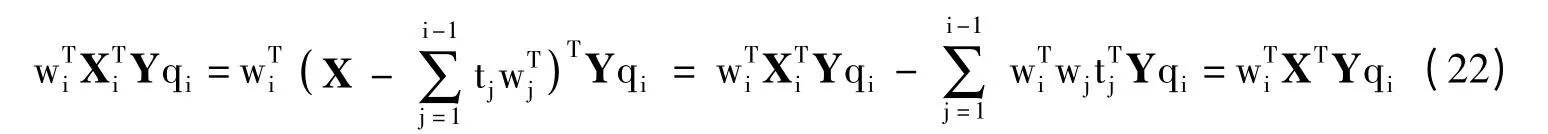
再对XTY 进行奇异值分解:

亦即:

其中，Σ=diag{σ1，σ2，…，σA}，wi和qi分别为对应σi的左奇异向量和右奇异向量。则称这种算法为加权PLS(W-PLS)。在W-PLS算法中，ti=Xwi，ui=Yqi，wi=pi。此时，目标函数为:

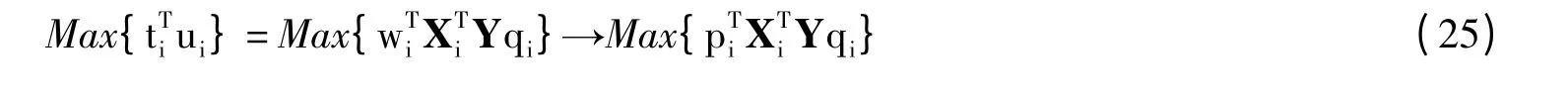
2 基于PLS的质量监测传统方法

长期以来，人们以一种类似PCA的方式在过程监控领域中使用PLS模型。具体做法是首先在与质量相关的过程潜变量子空间中建立Hotelling T2统计量和相应的控制限，并在与质量无关的过程残差子空间中建立平方预测误差(Squared Prediction Error，SPE)(也称Q 统计量)和相应的控制限，然后将观测向量分别向两个子空间中进行投影，再计算相应的统计量，并通过与控制限的比较来判断是否发生了异常。由于这两个统计指标是互补的，因此基于两者的混合指标也被用于故障检测[11]。Qin 将已有的故障检测指标表示成统一的形式[12]，方便了实际过程的应用。

Kresta 等最早将PLS 方法用于工业过程的监控[13]。随后，针对不同的过程运行特性或不同的过程监控目标，不少研究者对传统PLS 方法进行了不同程度的改进和推广。文献[14]采用核技术处理非线性问题，建立了核PLS 方法;结合小波变换，文献[15]研究了多尺度过程的故障诊断问题，建立多尺度PLS 方法;文献[16]考虑工业过程的慢时变特性，建立了用于自适应过程监控的递归方法PLS 方法;针对数据缺失或干扰，文献[17]建立了鲁棒PLS 方法;针对变量数目较大且可以分为若干子模块的大型复杂过程，文献[18]研究了多块PLS 方法，等等。

尽管PLS 方法在使用过程中得到了逐步地完善和发展，但是新的问题也在不断地涌现，集中体现在如下4个方面:1)需要较多的潜变量来描述与质量数据有关的变化，这其中包含了一些与质量数据Y 正交的变化，对预测Y 没有帮助;2)对过程数据X 分解后的残差矩阵中仍存在较大变化，该部分使用常规的Q 统计量并不合适[19];3)PLS与PCA的本质区别等方面没有得到彻底研究;4)不能处理同时具有多个稳定模态和多个过渡模态的多模态过程。为了解决上述几个问题，近年来提出了一些有效的质量监测方法，其中有的方法是针对其中一个典型的问题而开展的，有的方法则能够同时解决两个或两个以上典型的问题。接下来，将重点对这些方法进行总结和分析。

[21]Webb,S.(2005).Receptive and productive vocabulary learning.Studies in Second Language Acquisition,27,33-52.

3 基于PLS的质量监测扩展方法

依据上小节中所概括的4个问题，本节将对已有的解决方法进行梳理，主要包括全潜结构投影(Total PLS，T-PLS)方法、自回归潜结构投影方法、PLS与PCA的比较研究和基于PLS的多模态故障诊断方法，且对各种方法优缺点的分析也贯穿其中。

3.1 T-PLS 方法

为了去除潜变量空间中与质量正交的变化，Wold 等提出了正交信号修正方法(OSC)，基本思想是去除X 中和Y 不相关的变化，之后再对修正后的X数据进行PLS 回归[20]。Fearn 等进一步提出了另一种方法用来估计正交成分[21]。Trygg和Wold 提出了基于非线性迭代偏最小二乘算法的正交PLS(OPLS)算法，将数据X 中和Y 统计无关的成分滤除[22]。本质上来说，O-PLS算法是一种预处理方法，对于被过滤数据X的PLS 建模可以得到更为简单的模型。但是，上述算法都不是为了过程监控而提出的。Zhou[19]提出了一种全潜结构的投影算法(T-PLS)，该方法结合了PCA 能够去除变量间相关性的能力与PLS 能够抽取过程变量中与质量相关的子空间的能力，是在传统PLS 分解的基础上对质量变量的预测值进行PCA 变换，利用所抽取的潜变量再次引导过程变量的分解，将原始潜变量空间再次分解为与质量直接相关的子空间和与质量正交的子空间。同时，为了解决残差矩阵因含有较大变化而不适合用Q 统计量进行监测的问题，利用PCA 正交投影技术将残差空间再次分解为含较大方差变化的子空间和仅包含噪声的残差子空间。这样一来，只检测与质量有关的子空间和仅包含噪声的残差子空间便可知过程中是否发生与质量有关的故障。将T-PLS 应用于TE 过程案例研究中，有力地提高了与质量变量相关的故障检测率，降低了故障误报率。

进一步地，文献[23]基于贡献图建立了基于T-PLS的故障诊断方法。文献[24]研究了T-PLS 方法的故障可检测性，并基于质量相关的故障重构方法提出了联合监测指标。文献[25]针对质量监控中存在的非线性现象，提出一种核T-PLS 分解方法。文献[26]依据具有不同来源特征的多组过程变量，提出了T-PLS算法的多空间分解形式，将每一组过程变量中与质量相关的子空间分解为共有子空间和特定子空间，同时，将与质量无关的子空间分解为共有子空间，特定子空间和残差子空间，从而加强了对过程的理解并提高了实时监测的有效性。文献[27]从对质量变量进行全局监控的角度，认为质量变量是由可预测部分和不可预测部分组成，而T-PLS 方法仅仅对可预测部分的质量进行监控是不充分的，且过程变量分解为四部分监控子空间也是不必要的，为此，在T-PLS算法的基础上，提出了并行潜结构投影方法，对质量变量进行包含在线监控和离线监控的同时，也对过程变量进行重组，从而简化了T-PLS的模型结构。

尽管T-PLS 从过程监测的角度给出了划分检测子空间的方法，但是对于导致PLS 中潜变量空间包含与质量正交的变化的原因，并没有给出明确的解释。另外，由于潜变量个数的选取是受限的，因而理论上不能保证T-PLS 方法第三部分投影空间中发生的故障是和Y 完全无关的，而第四部分检测统计量超限也不能准确表明发生了与Y 有关的故障。为此，有待进一步研究如何更准确地划分检测子空间，以提高与质量有关故障的检测能力。

3.2 自回归潜结构投影方法

文献[28]分析了PLS 中潜变量空间之所以包含与质量正交的变化，在于其核心算法是基于非线性迭代偏最小二乘(NIPALS)的，在此基础上，利用自回归的思想提出一种改进的PLS 方法。该方法从原始数据出发，建立过程变量与质量变量之间的回归系数矩阵，利用SVD 分解技术提取潜变量投影空间，并对过程变量样本空间进行分解，避免了NIPALS的复杂计算过程。然而，与PLS 方法类似，此改进方法的残差空间同样包含方差较大的变化。在此基础上，受T-PLS 方法启发，文献[29]提出了另一种自回归全潜结构投影方法，利用质量变量的预测值来引导过程变量的分解，进而提取出与质量无关的过程残差中含有较大方差变化的部分。

分析可知，传统PLS是利用质量变量引导过程变量样本空间的分解，与之相应地，在最新的研究进展中，文献[19]和文献[28]都是利用质量变量的预测值来引导过程变量样本空间的分解，质量残差矩阵F代表了质量变量不能被过程变量所解释的部分。通常，并非全部过程变量的变化都影响质量变量，而对质量变量和过程变量的相关性来说，存在两种可能，要么其主要变化是由过程变量的变化引起的，残差F代表了质量变量的测量噪声;要么其部分变化能由过程变量所解释，而残差F代表了不能由过程变量所解释或没有被过程变量所充分激励的部分。针对质量变量的实时监测问题，根据质量变量与过程变量的相关关系分类，文献[30]提出了两种直接的潜变量空间分解方法。对于第一种情况，直接对质量变量进行PCA 分解，生成潜变量空间从而引导过程变量的分解;对于第二种情况，在建立质量变量和过程变量回归模型的基础上，对质量变量的预测值进行PCA 分解，给出一种直接用于质量监控的方法。这两种方法不仅解决了PLS 中潜变量空间含有与质量正交的变化以及残差空间含有较大方差变化的问题，而且模型简单，计算量小，既能有效检测出与质量变量相关的故障，更对实际的生产过程具有指导意义。

从实质来看，T-PLS 对质量的分解是基于PLS-PCA的，潜变量投影空间由(X，Y)共同决定，而文献[30]所提方法对质量的分解是基于PCA的，潜变量投影空间仅由Y 决定，这也从一定程度上验证了PLS 分解和PCA 分解有着重要的区别，尽管如此，对于PCA与PLS的本质区别等方面却没有得到彻底研究。

3.3 PLS与PCA的比较研究

PCA的基本做法是首先对正常过程的样本协方差阵进行特征值分解，其次对特征值大小进行排序，之后再根据能量大小选取维数较少的潜变量生成主元子空间，并最终将原始测量数据矩阵分解为主元部分和残差部分。从几何意义上来说，PCA的实质是坐标变换，即通过对以原始变量为坐标轴的原坐标系进行旋转，依次选取能够代表数据变异最大方向的坐标轴(即对应X 样本协方差阵的特征向量)作为主元方向。在PCA中，每一特征向量直接定义了X空间的一个分解结构。但是在PLS中，X空间的分解结构是由两个矩阵P和R 来定义的。因此，pi和ri之间的角度，反映了质量对X空间分解的影响。文献[31]分析了PLS算法对过程变量X空间分解的影响，指出这种影响取决于X的样本协方差矩阵的特征值相差是否很大，以及质量是否与主要的PCA 得分相关。如果质量与PCA的主要得分比较相关，那么PLS 对过程变量样本空间的分解结构与PCA的空间分解结构是类似的。这时，可以直接将PCA的方法应用于PLS的结构当中，但是如果质量与PCA的非主要得分比较相关，那么PLS的分解结构与PCA的分解结果具有明显区别。

3.4 基于PLS的多模态故障诊断方法

多模态过程具有以下特点:1)生产过程切换运行在多个稳定操作点之间，不同生产模态下，正常操作数据的均值、方差、相关关系等特性变量会有明显的变化;2)稳定模态是主要的生产状态，是决定产品质量的关键模态，且稳定模态下，过程变量的相关关系基本不变;3)过渡模态是衔接一个稳定模态到另一个稳定模态的暂态过程，它对生产效率影响较大，是实际生产过程中希望尽可能缩短的状态，且过渡模态下，过程变量的相关关系具有复杂的动态特性。

对多模态过程的质量监测研究主要集中在两点，离线建模和在线辨识。其中，对于稳定模态的建模研究相对较简单，成果也最多，对于过渡模态的建模研究仍是难点，而对于在线辨识的研究业已引起了人们的关注。文献[32]提出了一种pathway multiblock PLS算法，通过引入质量指标的中间测量值建立多个block PLS模型来分析各局部时间段内过程轨迹对于质量的影响效果，但是对于实际过程来说，质量的中间测量值很难获得，从而阻碍了该方法的广泛应用。文献[33]建立了基于时段的质量监测理论体系，提出了关键时段和关键变量的分析方法，为改善过程工艺设计、控制性能提供了重要信息，能够显著提升产品质量。其基本做法是首先提取各个时间片与最终产品质量的关联关系，然后通过相似性分析，自动划分影响产品质量的不同时段，再针对不同时段，建立不同的预测模型，当在线数据到来后将其在线匹配到质量预测时段模型，并最终实现产品质量的实时预报。然而上述基于硬时段划分的质量监测方法并没有考虑过渡时段特性，容易在时段边缘引起误报，为此，文献[34]通过引入软时段的概念，利用相邻时段特性模型联合表征过渡特性，建立了基于软过渡的质量分析与预测，进而提高了产品质量预测精度。

对于一般的多模态过程，稳定模态具有较长的运行时间，并且过渡模态具有明显的过渡特性，此时，大量的离线采样数据可被用来建立离线监测模型，并且待检测模态的在线辨识时间远远小于在线运行时间，虽然每个模态在运行初期，可能因检测模型不能及时跟上模态的切换过程，导致一定的错误监测结果，但从总体来看，由于传统方法能够对在线数据进行“量体裁衣”的监测，因而大多数的监测结果是满足系统要求的。然而，在工业生产过程中还常存在这样一类多模态过程，它同样具有多个稳定的生产模态和多个过渡模态，但是每个稳定模态运行时间短，采样数据少，过渡模态运行时间更短，采样数据更少，并且常在不同模态之间进行不断地切换。如何针对此类具有“快反应”特性的多模态过程进行过程监测是亟待解决的问题。Hwang与Han 通过假定不同的稳定模态具有共同的协方差结构，提出分层聚类超PCA模型，并应用于化工过程的实时监测，该方法避免了模型切换的现象，且由于计算量相对较小，因而具有实时性的优势，但是它却忽视了实际中多模态协方差结构可能有较大变化的问题，而且理论基础尚不完善[35]。文献[36]研究了间歇过程的在线辨识策略，即假定各个批次之间有相近的样本采样频率，若当前时刻采样点显示为异常，则需再匹配到下一模态的监控模型，若仍显示为异常，则判定系统出现异常。实际上，并非所有的多模态过程都具有固定的模态切换规律，而且受环境或原材料变化等因素的影响，不同批次的样本采样频率可能出现较大差异，进而给在线辨识增加了困难。针对具有“快反应”特征的多模态过程的监测问题，已经引起了广泛关注，但是其研究成果尚不多见。

4 结论和展望

PLS是质量监测的主流方法，在工业生产过程中有着广泛的应用。针对不同的应用对象和不同的监控目标，相关的方法也在不断地涌现、发展和完善。本文总结了基于PLS的质量监控方法，详细综述了T-PLS 方法和自回归潜结构投影方法，简要介绍了PLS 方法和PCA 方法的相似性和相异性，概括分析了基于PLS的多模态故障诊断方法。可以看出，相关领域的研究具有广阔的发展前景的同时，也充满了挑战，主要体现在相关的故障检测方法仍然面临很多科学问题，而故障诊断方法的研究成果相对较少。为了进一步提高对产品质量预测的可靠性，作者建议加强如下几个方面的研究:

1)PLS技术已经被成功并广泛地用于定量化提取过程变量与质量变量之间相随而动的因果关系。值得强调的是，建立过程变量与质量变量之间准确的回归系数是利用PLS技术分析并在线预测最终产品质量情况的关键因素。文献[19]利用NIPALS算法建立了回归系数，文献[28]在质量残差与过程变量无关的基础上，利用自回归技术建立了回归系数。理论分析表明若要监测是否发生了与质量有关的故障，仅需检验过程潜变量子空间中相应的统计量是否超出控制限即可。然而从仿真结果来看，无论PLS、T-PLS 或是改进的潜结构投影方法都联合使用了过程潜变量子空间和过程残差子空间。因此，有必要深入分析子空间分解对质量监测能力的影响，进而研究如何获得精确的回归系数以提高与质量相关的故障诊断率;

2)尽管已有大量的相关文献报道，但是多数故障诊断方法都是在变量具有一致重要性的基础上提出来的。而实际的生产过程中，每个变量对产品质量的影响程度是不同的，变量的重要性也就不同。那么，如何针对不同的过程变量或质量变量，定义其影响产品质量的相对重要性，进而将相对重要性引入到质量相关的故障诊断中，必将具有重要的理论研究意义和实际研究价值;

3)现有基于PLS的多模态故障诊断方法均仅考虑一个多模态过程，而在实际的工业生产过程中，常常呈现出由多个子系统相互耦合作用而导致的多个多模态现象。如机械加工电力拖动系统包含切削子系统和电动机子系统，对同一工件进行粗细加工的切削过程为多模态工况，具有多模态和周期性等特点，其中车床的工作模态有前刀架、后刀架和主轴旋转进给等;电动机受系统切削的需求被动地运行在启动、空载、加载、减载、调速和制动等模态;电动机模态与切削系统需求模态经传动耦合又呈现双多模态过程。因此，不仅要考虑每一个子系统的多模态现象，还要同时考虑双多模态过程相互间的关联性和系统中不同装置的联接和过程变量强耦合关系导致更为复杂的故障的传播与演化。目前，从系统层面研究复杂工业过程的质量监测和诊断问题，成果尚不多见。因此，研究如何对多个多模态过程进行建模，进而提取能反映真实故障方向的潜变量投影子空间，是提高生产产品质量乃至整个系统安全运行需亟待解决的问题;

4)报警问题。目前的过程监控都是基于诊断的，一旦出现异常点即认为发生了故障，而实际工业过程中报警系统的设计是很有应用意义的。面对海量的采样数据，报警器基于判定所发出的警报，对于操作者实时掌握设备的运行状况，及时觉察异常起到了关键的作用。这其中若发生误报将增加操作人员的负担，若发生漏报将可能引起生产的高成本损失乃至灾难性后果。真正报警系统在实现上要复杂的多，主要原因有:(1)受设备老化或磨损，环境的变化及噪声干扰等不确定性因素的影响;(2)包含过程数据，工艺数据等不同来源的数据类型不统一;(3)系统运行具有多阶段特性。为此，如何设计一类高可靠度的报警器，是值得深入研究的课题;

5)众所周知，大数据时代已经到来，因此，基于大数据的控制、决策、调度与故障诊断已成为新的热点和重要研究方向，而基于大数据的实时检测、故障诊断、及时监控和报警也必将成为重要的研究内容之一。当前，基于大数据的各类方法的研究核心是高效率和低成本，即重点解决在有限时间内用现有方法所不能及时处理的问题;如之前的电力系统采样通常是秒级，而新的采样装置已经可以达到毫秒级，若考虑几万，几十万甚至上百万个网络节点组成的传感器采样系统，而研究的对象是智能调度和实时监控，那么这就是一个典型的大数据问题。因此，基于大数据的故障诊断将要解决的主要问题有:(1)建立什么样的新方法以适应大数据处理过程中的快速有效性;(2)如何开展大数据的有效约简和表示，以适用于现有的方法。

[1]宋凯.基于PLS的统计质量监控研究与应用[D].杭州:浙江大学，2005:1-10.

[2]周东华，李钢，李元.数据驱动的工业过程故障诊断与预测技术——基于PCA与PLS的方法[M].北京:科学出版社:2011.

[3]Russell E，Chiang L H，Braatz R D.Data-driven methods for fault detection and diagnosis in chemical processes[M].New York:Springer，2000.

[4]Jolliffe I.Principal component analysis[M].John Wiley ＆ Sons，Ltd，2005.

[5]Qin S J.Data-driven fault detection and diagnosis for complex industrial process[J].Fault Detection，Supervision and Safety of Technical Processes.2009:1 115-1 125.

[6]Kadlec P，Gabrys B，Strandt S.Data-driven soft sensors in the process industry[J].Computers ＆ Chemical Engineering，2009，33(4):795-814.

[7]Kano M，Nakagawa Y.Data-based process monitoring，process control，and quality improvement:recent developments and applications in steel industry[J].Computers ＆ Chemical Engineering，2008，32(1):12-24.

[8]MacGregor J F，Kourti T.Statistical process control of multivariate processes[J].Control Engineering Practice，1995，3(3):403-414.

[9]Dayal B，MacGregor J F.Improved PLS algorithms[J].Journal of Chemometrics，1997，11(1):73-85.

[10]Li G，Qin S J，Zhou D.Geometric properties of partial least squares for process monitoring[J].Automatica，2010，46(1):204-210.

[11]Yue H H，Qin S J.Reconstruction-based fault identification using a combined index[J].Industrial ＆ engineering chemistry research，40(20)，2001:4 403-4 414.

[12]Joe Qin S.Statistical process monitoring:basics and beyond[J].Journal of Chemometrics，2003，17(8-9):480-502.

[13]Kresta J V，MacGregor J F，Marlin T E.Multivariate statistical monitoring of process operating performance[J].The Canadian Journal of Chemical Engineering，1991，69(1):35-47.

[14]Lindgren F，Geladi P，Wold S.The kernel algorithm for PLS[J].Journal of Chemometrics，1993，7(1):45-59.

[15]Lee H W，Lee M W，Park J M.Multi-scale extension of PLS algorithm for advanced on-line process monitoring[J].Chemometrics and Intelligent Laboratory Systems，2009，98(2):201-212.

[16]Joe Qin S.Recursive PLS algorithms for adaptive data modeling[J].Computers ＆ Chemical Engineering，1998，22(4):503-514.

[17]Wakelinc I N，Macfie H J H.A robust PLS procedure[J].Journal of Chemometrics，1992，6(4):189-198.

[18]MacGregor J F，Jaeckle C，Kiparissides C，et al.Process monitoring and diagnosis by multiblock PLS methods[J].AIChE Journal，1994，40(5):826-838.

[19]Zhou D，Li G，Qin S J.Total projection to latent structures for process monitoring[J].AIChE Journal，2010，56(1):168-178.

[20]Wold S，Antti H，Lindgren F，et al.Orthogonal signal correction of near-infrared spectra[J].Chemometrics and Intelligent Laboratory Systems，1998，4(1):175-185.

[21]Fearn T.On orthogonal signal correction[J].Chemometrics and Intelligent Laboratory Systems，2000，50(1):47-52.

[22]Trygg J，Wold S.Orthogonal projections to latent structures (O-PLS)[J].Journal of Chemometrics，2002，16(3):119-128.

[23]Li G，Qin S Z，Ji Y D，et al.Total PLS based contribution plots for fault diagnosis[J].Acta Automatica Sinica，2009，35(6):759-765.

[24]Li G，Joe Qin S，Zhou D.Output relevant fault reconstruction and fault subspace extraction in total projection to latent structures models[J].Industrial ＆ Engineering Chemistry Research，2010，49(19):9 175-9 183.

[25]Peng K，Zhang K，Li G.Quality-related process monitoring based on total kernel PLS model and its industrial application[J].Mathematical Problems in Engineering，2013，2013.

[26]Zhao C H，Sum Y X.The multi-space generalization of total projection to latent structures(MsT-PLS)and its application to online process monitoring[C]//Control and Automation (ICCA)，2013 10th IEEE International Conference on.IEEE，2013:1 441-1 446.

[27]Qin S J，Zheng Y Y.Quality-relevant and process-relevant fault monitoring with concurrent projection to latent structures[J].AIChE Journal，2013，59(2):496-504.

[28]Yim S，Ding S X，Zhang P，et al.Study on modifications of PLS approach for process monitoring[C].Preprints of 18th IFAC world congress，2011:12 389-12 394.

[29]苑天琪，胡静，文成林.自回归全潜结构投影模型及其在过程监控上的应用[C].Proceedings of 32th Chinese Control Conference，2013:6 267-6 271.

[30]Hu J，Wen C L，Li P，et al.Direct projection to latent variable space for fault detection[J].Journal of the Franklin Institute，2013:1 226-1 250.

[31]Li G，Qin S J，Zhou D H.Geometric properties of partial least squares for process monitoring[J].Automatica，2010，46(1):204-210.

[32]Duchesne C，MacGregor J F.Multivariate analysis and optimization of process variable trajectories for batch processes[J].Chemometrics and Intelligent Laboratory Systems，2000，51(1):125-137.

[33]Zhao C H，Gao F R.SpectraCalibration Modeling and Statistical Analysis for Cumulative Quality Interpretation and Prediction[J].AIChE Journal，2012，58(2):466-479.

[34]Zhao C H，Gao F R，Sun Y X.Between-phase calibration modeling and transition analysis for phase-based quality interpretation and prediction[J].AIChE Journal，2013，59(1):108-119.

[35]Hwang D H，Han C H.Real-time monitoring for a process with multiple operating modes[J].Control Engineering Practice，1999，7(7):891-902.

[36]Zhao C H，Mo S Y，Gao F R，et al.Statistical analysis and online monitoring for handling multiphase batch processes with varying durations[J].Journal of Process Control，2011，21(6):817-829.