基于随机共振原理的低频弱信号检测方法研究
(杭州电子科技大学机械工程学院,浙江 杭州310018)
0 引 言
随机共振在检测强噪声背景环境下的信号方面具有独特的优势,尤其是当噪声达到某一适当强度时,非线性系统、信号与噪声共同作用将一部分噪声转化成为信号。非线性系统的响应机理在一定范围内可以用绝热近似[1]及线性响应理论来阐明,近年这个理论正在不断地完善和发展并推广到各个领域,如多稳态系统的研究[2]、基于随机共振原理的二维图像处理[3]、H-H神经元模型的研究[4]、基于随机共振原理的自适应检测方法的探索[5],但是这些理论仅适应于小参数信号(小噪声、极低频率、小幅度)[6],而在实际情况中,信号的参数可能较大。本文在分析了基本双稳随机共振系统模型的基础上,提出了一种新的调参模型,此模型能够实现识别较高频率的微弱信号。
1 基本双稳系统的随机共振
随机共振模型需要3个要素,分别是非线性系统、输入驱动信号以及噪声。若以最基础双稳非线性系统,单频正弦信号和高斯白噪声为研究对象,该共振模型可用郎之万方程描述为:

式中,μ >0,A为信号幅值,f为信号频率,n(t)为高斯白噪声。n(t)满足:

式中,D为噪声强度,为时间延迟。在绝热近似环境下,模型的S(f)由两部分内容构成:
1)由驱动正弦信号引起的S1(f);
2)由噪声引起的具有洛伦兹形式[7]的S2(f)。
且噪声功率谱S2(f)与信噪比SNR的计算公式分别为:

若对N点的信号y()进行离散傅里叶变换可得Y(f),则有:

式中,P总为总信号频谱,SN为噪声能量,SNR为信噪比。
2 新双稳系统模型
在仿真工作中,遇到的信号频率往往超出上述频率范围,所以本文提出了新的随机共振系统模型。其动力学方程可表示为:
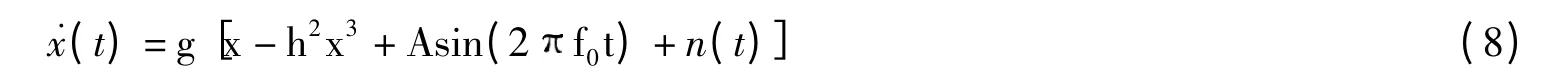

整理后,可得:
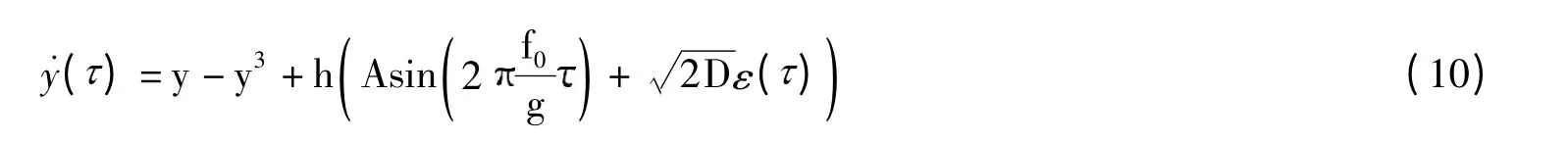
可以看出,当h=1时,式(10)即为上面提到的郎之万方程(其中μ =1)。对比式(8)和式(10)可看到,双稳系统经过变换后,输入信号的频率变为原来的1/g,信号与噪声幅值变为原来的h倍。两方程是等价的,因此在检测强噪声背景中的中低频信号时,可通过选择合适的参数g和h,将信号变换为低频信号后,再进行处理。由式(10)可以看出,调节参数g 只影响信号的频率,调节参数h 只影响信号与噪声的幅值。
通过数值仿真实验来检验上述双稳随机共振系统模型能否识别中低频小信号,以及验证各参数对系统的影响。对应于式(8),若g =100,h =1,f0=1 Hz,则fs=200 Hz,A =0.37,D =0.2;则对应于式(1)各参数取值为:μ=1,A=0.37,f0=0.01 Hz,D=0.2,fs=2 Hz,将这些参数分别代入对应方程中,再分别对方程采用四阶Runge-Kutt(a)方法计算,按式(5)计算输出频率幅值,具体结果如图1所示。
其中图1(a)为输入时频域波形图,图1(b)图与1(c)分别为式(8)与式(1)的输出时频域波形图。从图1(a)的时域波形图中无法看出有周期信号存在,而图1(b)、图1(c)显示,系统的时域输出为周期震荡信号,且输出频域图在某一频率处有一明显的尖峰。说明两系统均发生了随机共振现象。而且二者的时频域图形极为类似,证明了此参数变换的可行性,同时也说明了增大g,可提高发生随机共振的共振频率;反之亦然。另外,由于式(10)中,输入信号的实际频率为f0/g =0.01 Hz,所以采样频率可取fs=2 Hz,且图1(b)与1(c)中输出仿真信号的频谱在0.01 Hz 处有一尖峰,说明发生共振的输入信号频率为0.01 Hz。
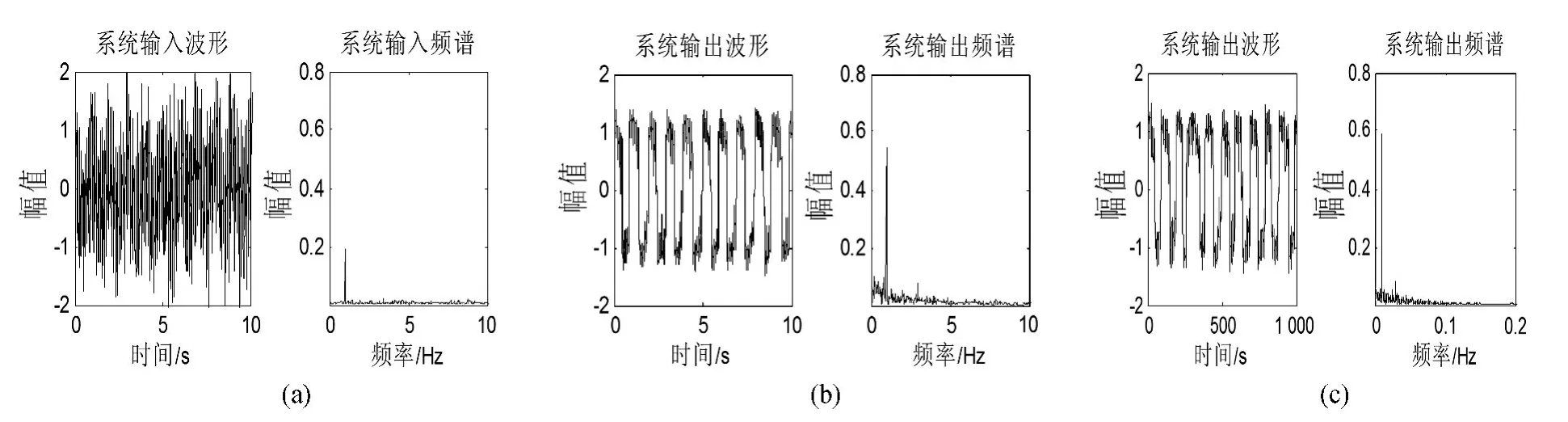
图1 系统输入输出时频域波形图
若g=100,h=2,f0=1 Hz,对应于式(8)有fs=200 Hz,A =0.185,D =0.05;对应于式(10)有fs=2 Hz,A=0.185,D=0.05,将这些参数分别代入对应方程中,再分别对两方程采用四阶Runge-Kutt(a)方法计算,按式(3)计算输出频域幅值,具体结果如图2所示。
图2(a)与2(b)的输出波形显示两系统均发生了随机共振现象,且2 者的图形极为类似,但是图2(a)中的输出信号时频域幅值都较图2(b)中的值小,这是由于图2(a)中的输出为x,而图2(b)中的输出为y,由式(9)不难证明此结论。由两系统的混合输入信号说明增大h,可检测小幅值,低噪声强度的信号;反之亦然。

图2 系统输出时频域波形图
根据原有的输出信号功率谱公式和信噪比公式,推导出新模型的输出信号功率谱公式和信噪比公式。分别结合式(10)与式(3),求得功率谱Sy2(f),结合式(10)与式(4),求得输出信噪比SNR2。设Sx2(k)是式(8)中由噪声引起的功率谱,结合功率谱的定义与式(9)可得:

计算得到:

分别计算式(1)、式(8)与式(10)的噪声输出功率谱,并进行仿真实验对比,如图3所示。图3中,图3(a)、(b)、(c)中参数取值分别与图1(b)、图1(c)、图2(a)中参数的值相同。S12为仿真输出功率谱的平滑曲线,S22为理论输出噪声功率谱值。可见仿真信号输出与理论分析结果一致。对比图3(b)与图3(c)可发现,两个模型的图形类似,但图3(c)中的噪声幅值是图3(b)的倍,验证了h的变化对系统的影响;对比图3(b)与图3(a)可发现,图3(a)中各幅值对应的频率值是图3(b)中的g =100倍,验证了h的变化对系统输出的影响。

图3 仿真信号的噪声输出能量谱与理论信号的噪声输出功率谱对比图
图4分别为由式(8)与式(10)中的输出信噪比随噪声变化的仿真值与理论值的对比图,图4中,图4(a)、(b)中参数取值分别与图3(a)、(c)中参数的值相同。SNR1为5次输出信噪比随噪声变化的仿真值的平均值,SNR2为输出信噪比随噪声变化的理论值。可见信号仿真输出与理论分析结果一致。对比图4(a)与图4(b)可发现,二者最大信噪比值所对应的噪声强度不同,这与理论分析结果一致。
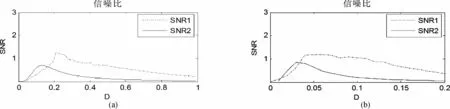
图4 仿真信号与理论信号的输出信噪比随噪声变化对比图
所以,在一些参数已知的情况下,可以有针对性地调节参数,以提高检测信号的速度。
3 结束语
本文分析了基本的双稳系统产生随机共振的条件以及系统本身的缺陷。在原有模型的基础上,提出了一种新的模型,此模型可实现强噪声背景下的中低频率信号检测,并推导出了此模型的功率谱与信噪比随噪声的变化的公式,且举出实例对公式进行了验证,而且通过调节参数可实现检测多组不同混合信号中的周期信号。本文的研究拓宽了随机共振产生的条件,在大参数周期信号的检测与增强中具有一定的物理意义和实用价值。
[1]胡岗.随机力与非线性系统[M].上海:上海科技教育出版社,1994:219-240.
[2]Matyjas' kiewicy S,Krawiecki A,Ho yst J A,et al.Stochastic multiresonance in a chaotic map with fractal basins of attraction[J].Physical Review E,2001,63(2):6 215-6 225.
[3]Janpaibon S,Mitaim S.Adaptive stochastic resonance in color object segmentation[J].Neural Networks,2006,16(21):2 508-2 515.
[4]Tai C,Groat W,Roppolo J,et al.Simulation of nerve block by high-frequency sinusoidal electrical current based on the Hodgkin-Huxley model[J].IEEE Transactions on Neurall Systems and Rehabilitation Engineeering,2005,13(3):415-422.
[5]方倩,赵文礼.基于随机共振原理的自适应检测系统影响[J].杭州电子科技大学学报,2013,33(1):68-72.
[6]冷永刚,王太勇,郭焱,等.双稳随机共振参数特性的研究[J].物理学报,2007,56(1):30-35.
[7]冷永刚,王太勇.二次采样用于随机共振从强噪声中提取弱信号的数值研究[J].物理学报,2003,52(10):2 432-2 437.

