改进的Tent映射及其动力学特性研究

(杭州电子科技大学电子信息学院，浙江 杭州310018)

0 引 言

在非线性科学中，混沌以及混沌系统的发现是近代重要成就之一。混沌所具有的随机特性可用以产生伪随机序列从而应用于保密通信和信息加密之中。Tent映射(帐篷映射)是一个算法简单但序列复杂的离散映射，用其产生伪随机序列具有运算速度快、序列分布均匀的优势[1]。因此，Tent映射在混沌保密通信和混沌密码设计中得到了广泛的应用[2-3]。但帐篷映射存在参数少、映射范围小等缺陷，将直接导致产生的伪随机序列密钥空间小，安全性变差[4-5]。为此，本文对原始的Tent映射做了改进。改进后的Tent映射增加了两个参数，除保留其分布均匀的优势外，参数空间和映射范围都得了明显的扩展。

1 Tent映射

Tent映射，如下所示:

式中，x(n)∈(0，1)，u∈(0，2)，当u ＞1时，系统是处于混沌状态，其分叉图如图1所示。其满映射区间以及参数u的范围都比较小，导致由此映射产生的序列密钥空间也会比较小[6]。

图1 Tent映射分叉图

2 改进的Tent映射

为了增加参数和扩展满映射范围，对Tent映射改进如下:

式中，x(n)∈(0，a)，u1∈(0，2)，u2∈(0，2)，a ∈R。虽然只增加了几个参数，但改进的Tent映射却增加了复杂的动力学特性。式(2)中的a 被称之为幅度参数，因为满映射的幅度即最大的映射范围与a 有关。尤其当u1=u2=2时，满映射幅度a的分叉图如图2(a)所示，不但满映射幅度随参数a 比例增加而增加，且随a的变化过程中，映射始终是混沌的。如果以a 作为密钥参数，理论上该参数对应的密钥空间趋于无穷，即a∈(0，∞)。保持参数a、u2为固定值，观察映射随参数u1变化的分叉情况。仿真发现，当u1＞1时映射是混沌的，当u1=2时为满映射，满映射幅度为a，出现混沌的u1参数区间为u1∈(1，2)。图2(b)为u2=2、a=3时的分叉图。保持参数a、u1为固定值，观察映射随参数u2变化的分叉情况。仿真发现，当u2＞1时映射是混沌的，混沌映射的大小随u2的增加而减小，但其混沌映射区间则维持不变，映射区间长度为a，出现混沌的u2参数区间为u2∈(1，2)。图2(c)为u1=2、a =4时的分叉图。保持参数a为固定值，当u1=u2=u，a =4时，观察映射随参数u 变化的分叉情况。此时除满映射幅度等于a 外，其分叉情况与原始的Tent映射相同，只是满映射的幅度不同，如图2(d)所示。

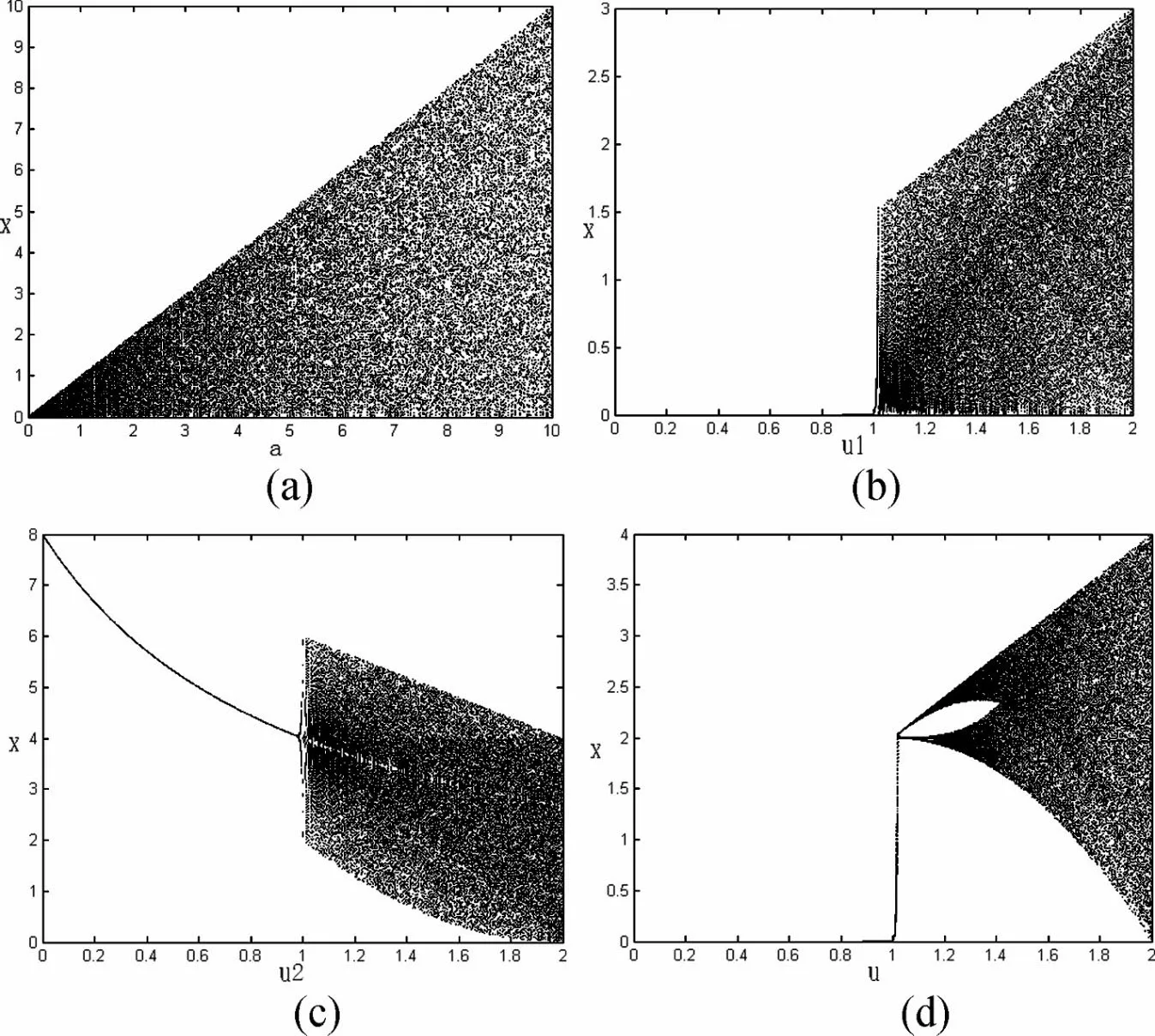
图2 改进型Tent映射分叉图

Tent映射最大优点是具有良好的随机特性，其迭代值近似均匀分布，图3是Tent映射在满映射区间[0，1]的分布柱状图，u=2.0，x(0)=0.01，把0 1 均匀分为50 等份，均匀特性如图3(a)所示。表1为映射在这些区间分布次数的具体值，计算得到的数据标准差为S =93.48。图3(b)为改进的Tent映射当u1=u2=2.0，a=16时，在满映射区间[0，16]的分布柱状图，表2为映射在这些区间分布次数的具体值，计算得到的数据标准差为S=115.31。

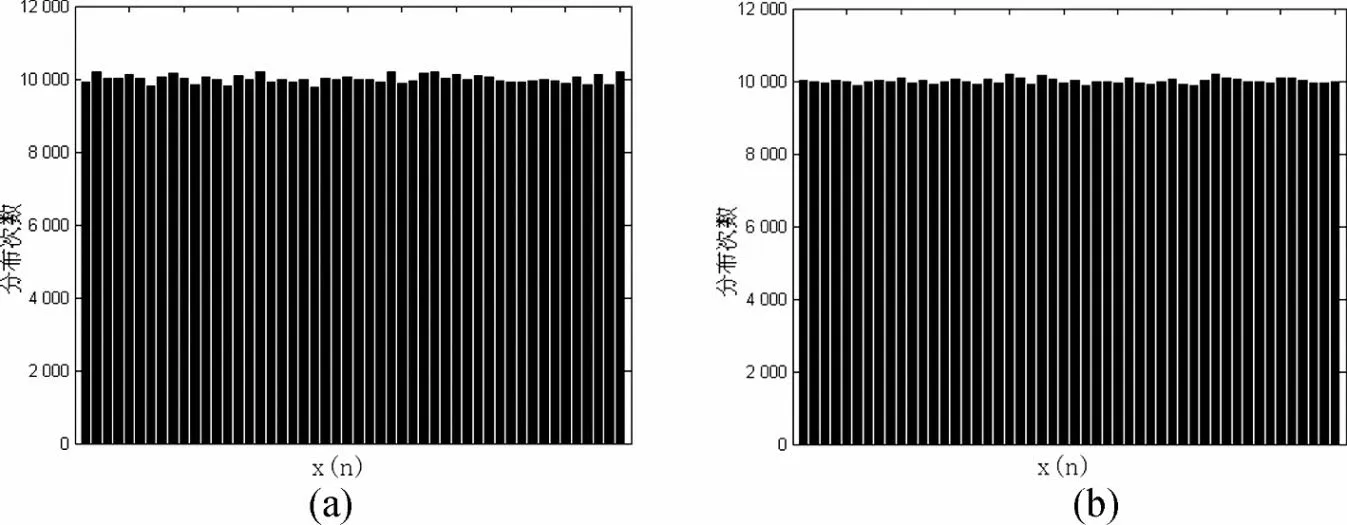
图3 映射分布柱状图

表1 帐篷映射迭代50万次后，迭代值分布具体数据与方差

表2 幅度改进型帐篷映射(a=16) 迭代50万次后，迭代值分布具体数据与方差

比较得知，改进后的映射分布保持了原来的均匀特性，能够使迭代值更加均匀的分布在一个更大的范围内。如果使用此改进映射产生的混沌序列进行加密，能够使得整个系统的密钥空间更大，具有更好的安全性。

美国国家技术与标准局推出的测试程序包(Statistical Test Suite)是目前对为随机序列性能测试工具中最具有权威的一种。本文采用sts2.1.1 测试软件包对改进Tent映射的数字序列进行了测试，该软件包含16 项测试[7]，其中有15 项是对伪随机序列性能进行测试的指标，测试结果如表3所示。测试是在4×107bit数据下进行的，分2 000组，每组20 000 bit数据。

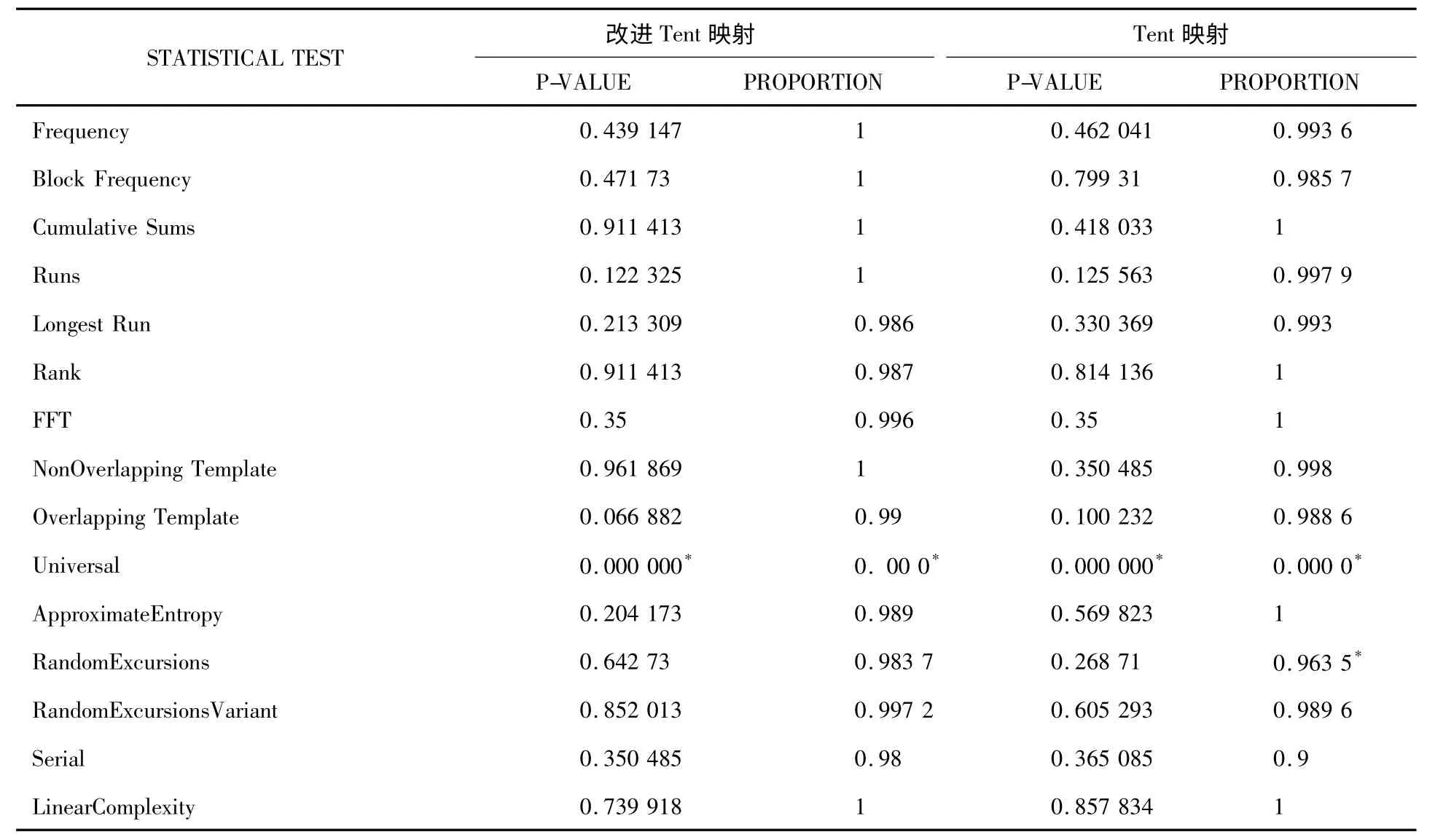
表3 STS 测试结果报告

从通过率来看，只有通用统计测试没有通过，其它测试项都通过了测试，从均匀性来看，也只有通用统计测试没有通过，其余项的均匀性都较为良好。总体来说，改进前后映射产生的序列性能都比较良好，能够使用这些映射产生为随机序列运用到实际加密当中。

3 结束语

本文构造了一种新的改进型Tent映射，通过分析、仿真以及各个参数的分叉图等对它的一些基本性质进行了研究。数值仿真实验结果表明，改进后的Tent映射即保持了原始Tent映射产生伪随机序列速度快、序列在映射区间内分布均匀的优点，又改善了原始Tent映射参数区间和满映射区间小的缺点，增强了序列的随机特性、扩展了序列的密钥空间。由于改进型Tent映射具有更加复杂的动力学行为特性，因此改进型Tent映射将能更好地应用在混沌保密通信和混沌密码设计中。

[1]Nejati H，Beirami A，Massoud Y.A Realizable Modified Tent Map for True Random Number Generation[J].51ST Midwest symposium on circuits and systems，2008，1(1):621-624.

[2]Shan L，Qiang H，LI J，et al.Chaotic Optimization Algorithm based on Tent map[J].Control and Decision，2005，20(2):179-82.

[3]Xu Z G，Tian Q，Tian L.A class of topologically conjugated chaotic maps of tent map to generate independently and uniformly distributed chaotic key stream[J].Acta Physica Sinica，2013，62(12):12 050.

[4]Chen S L，Chang S M.Digital Secure-Communication using Robust Hyper-Chaotic Systems[J].International Journal of Bifurcation and Chaos，2008，18(11):3 325-3 339.

[5]Luca A，Ilyas A，Vlad A.Generating random binary sequences using tent map[C].Iasi:Signals，Circuits and Systems(ISSCS)，2011:1-4.

[6]Zhang X F，Fan J L.Extended Logistic Chaotic Sequence and Its Performance Analysis[J].TsingHua Science and technology，2007，12:156-161.

[7]Andrew R，Juan S，James N，et al.Statistical Test Suit for Random and Pseudorandom Number Generator for Cryptographic Applications[J].NIST Special Publication，2001，1(1):800-822.