基于T-S模型的随机双线性系统的稳定问题
(杭州电子科技大学,浙江 杭州310018)
0 引 言
双线性系统介于线性系统和非线性系统之间,其动态要比非线性的简单,并且双线性系统比线性系统更好地逼近非线性系统,许多实际的物理过程不能够用线性系统描述,但是可通过适当地建模,用双线性系统表示。由于这两个优点,对双线性系统的稳定性分析和控制器设计显得尤为重要。研究非线性系统比较有效的方法是T-S模型的模糊控制,在此方法上研究的成果[1-4]已有很多。文献[1]首次提出了T-S 模糊双线性系统。目前关于T-S 模糊随机双线性系统的研究成果并不多,因此在该文中,根据It^o 随机稳定性理论的相关知识,采用并行分布补偿方法、Lyapunov 函数法等方法研究基于T-S模型的随机双线性系统的稳定性问题。
1 系统描述

式中,x∈Rn是状态向量,u∈R是控制输入,ω(t)∈R是标准维纳过程,Ai,Bi,Ci,Ni是已知的具有适当维数的实常数矩阵;r是If-Then 规则数,ξ(t)=(ξ1(t),…,ξr(t))T是前提变量向量,Fi1,Fi2,…,是模糊集合。
由上述模糊规则描述的系统得到的模糊随机双线性系统为:
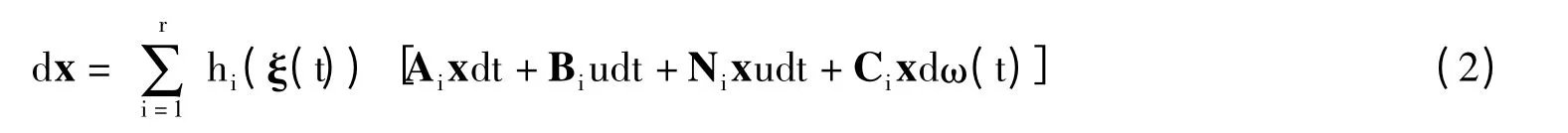
采用文献[5]的设计概念,模糊控制器的描述为Control rule j:If ξ1(t)is Fj1,and…,and ξr(t)is Fj,
全局控制器可以表示为:
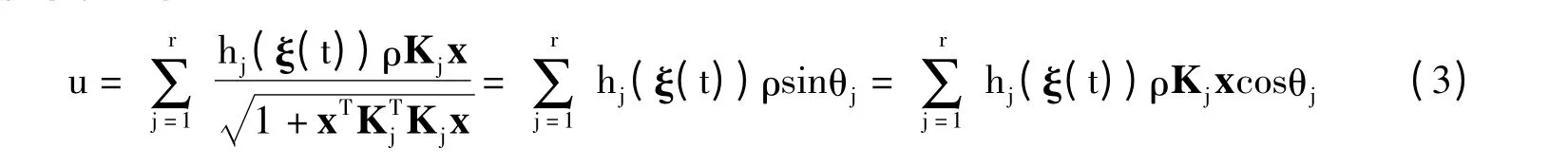
把式(3)带入式(2),得到的闭环系统方程为:

考虑定义在Rn上的随机微分方程[6]:

引理1[6]若存在正定函数V(x,t)∈C2,1(Sh×[t0,∞);R+)是径向无界、上下有界的,对所有的(x,t)∈Sh×[t0,∞),如果那么随机系统式(5)是大范围随机渐近稳定的。
2 主要结果

那么闭环系统式(4)是大范围随机渐近稳定的。
证明 考虑二次型的Lyapunov 函数V(x)=xTPx,其中P是满足矩阵不等式(6)、式(7)的正定矩阵。显然,V(x)是正定的且是径向无界的。微分算子沿着式(4)的轨迹作用在函数V(x)上,则:

对于式(8)中的若干项应用不等式ATB+ABT<γATA+γ-1BBT,得P(Ai+BiKiρcosθi+Niρsinθi)+
由此可得:

对式(7)采用Schur 补引理,结合式(8)中的另一些项,同理得:

3 数值实例
4 结束语
[1]Li T S,Tsai S H.T-S Fuzzy Bilinear Model and Fuzzy Controller Design for a Class of Nonlinear Systems[J].IEEE Transactions on Fuzzy Systems,2007,15(3):494-506.
[2]Dong J,Yang G H.State Feedback Control of Continuous-time T-S Fuzzy Systems via Switched Fuzzy Controllers[J].Information Sciences,2008,178(6):1 680-1 695.
[3]Zhou S S,Lam J,Zheng W X.Control Design for Fuzzy Systems Based on Relaxed Nonquadratic Stibility and H∞Performance Conditions[J].IEEE Transactions on Fuzzy Systems,2007,15(2):188-199.
[4]Zhou S,Ren W Y,Lam J.Stabilization for T-S Model Based Uncertain Stochastic Systems[J].Information Sciences,2011,181(4):779-791.
[5]Chiou J S,Kung F C,Li T S.Robust Stabilization of a Class of Singularly Perturbed Discrete Bilinear Systems[J].IEEE Transactions on Automatic Control,2000,45(6):1 187-1 191.
[6]Mao X.Stochastic Differential Equations and Applications[M].Chichester:Horwood Pubication,1997:107-146.

