《线性代数》教学中学生创新意识和创新精神的培养

潘大勇，陈忠

（长江大学信息与数学学院，湖北 荆州434023）

《线性代数》是高等院校普遍开设的一门重要的必修基础课，在现代物理、化学、计算机科学、通讯技术、工商管理、资源勘查、石油工程等领域的应用越来越广泛，发挥无可替代的重要作用。教学过程中，在传授基础知识、基本方法和基本技能的同时，如何着力培养学生的创新意识和创新精神，是每个教师在教学中都应当认真思考的重要课题。

1 在新旧知识的衔接处培养学生的创新意识和创新精神

在讲授知识过程中，要引导学生感受 《线性代数》中的一些概念和方法是如何产生出来的，感受学科发展过程中孕育的创新精神和力量。

解线性方程组是 《线性代数》的一个中心课题，是 《线性代数》发展的原动力之一。行列式的概念就是在求解二元一次线性方程组、三元一次线性方程组（方程的个数和未知数的个数相同）所使用的高斯消元法的基础上引入的。如果只是简单地告诉学生结论，而置知识产生的背景和萌生的思想而不顾，学生就难以理解要引入一个新的概念和方法的必要性。因此，让学生感知创新意识的土壤在哪里是很重要的。如果理解了二阶、三阶行列式的实质，学生自然而然就能理解一般意义的n阶行列式了。

探究发现，克莱姆（Cramer）法则只能解决方程个数与未知数个数相同的线性方程组的情形，而且对于解不唯一时怎么表示通解等都有很大的局限性，这就会引发新的思考和探究，如何才能更一般地解决线性方程组的求解问题？引入矩阵及初等变换这个新的工具，学生就能理解这样做的必要了。借助矩阵的初等变换和矩阵的秩，不仅可以判别一般的线性方程组的解的存在性，而且可以给出解的表达式。对于线性方程组有无穷多解的情形，解与解之间的关系如何呢？如何表示解之间的关系呢？换句话说，能否用有限多个解去表示无穷多个解呢？这样的问题又可引发出向量组的线性相关性理论和线性方程组解的结构理论。这样一种在新旧知识交汇衔接处提出问题，渗透创新意识，培养创新精神都是大有潜力可以发掘的。

2 在探究知识的过程中培养学生的创新意识和创新精神

在通常的教材中，《线性代数》都是演绎结构，每章（节）大致上是按定义、性质、定理或公式、求解等基本环节来呈现［1－2］。演绎体系逻辑性强，条理脉络清晰，内容紧凑精炼，但不可回避的是，学生往往觉得难以理解并有种压迫感，和书本产生很强的距离感，总会有一个个问题萦绕在心头：编著者为什么这样写呢？这些结果是怎么想到的呢？如果能够将数学家在建构相关知识时所作的 “火热思考”［3］再现出来，学生学到的不仅仅是一些结果，而且能够感受数学家的创新思维过程。

矩阵是 《线性代数》的核心概念，那么为什么会有这样一个概念呢？矩阵的本质是什么？矩阵其实就是一个数表，存在于生活的方方面面。上课的课表、成绩单（文字本质上也可以数字化）、科研数据等各种表格以及照片（黑白照片从数学角度看其实是一个数表，每个点都可以用0～255中某个整数表示其灰度值，彩色照片则是由红绿蓝3种基色复合而成的三维的数表）等等都可以用矩阵表示。既然用矩阵表示数表，那么是否可以用矩阵来描述数表的运动变换呢？如把一张图片放大2倍，或是把一张图片逆时针旋转90°，等等，这就涉及到矩阵的运算及其性质了。这些内容对于第一次接触的学生而言，好比当年数学家们首先发现、探究一样，是一种全新的挑战，是一次创新之旅，无论是方法还是思想，无不深深阐发出创新的精神，这对学生的创新意识的影响是重要和深远的。学生重走前人的路，并不是简单的重复，其实也是一次发现之旅，探索之旅，创新体验之旅，成长收获之旅。从这个意义上讲，老师的引导和启迪是十分关键的，如果教师满堂灌，学生缺少独立思维活动，其实就是剥夺了学生的创新意识的产生。如果所有结论总是以完整的形式出现，学生知其然，而不知其所以然，体验不到探索和发现的过程，长此以往，不利于学生发现、探索能力的培养，也不利于学生抽象、归纳、概括能力的培养，更不利于创新意识和创新精神的培养。

3 在应用知识解决问题的情境中培养学生的创新思维意识

当前，《线性代数》的教学相对偏重自身的理论体系，强调基本定义、定理和基本思想，实际应用讲的较少，应用类的课后习题也少得可怜.这导致大部分学生不了解线性代数对后续专业课学习，也在一定程度上影响专业课的学习质量［4］。因此，《线性代数》的学习，不单是培养学生的逻辑思维能力，而且还应当重视它的广泛应用，在应用中锻炼学生的数学眼光和数学思考，培养学生发现并提出相应的数学问题（或数学模型）的意识，应用数学方法去解决问题的能力。教学中要秉承这样的理念，提升应用意识。

以矩阵乘法和线性变换这个知识点为例，在教学中可以结合具体问题来激发学生创新思维的 “火热思考”。如：

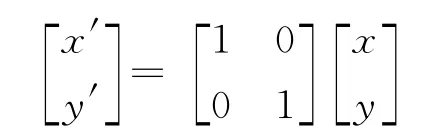
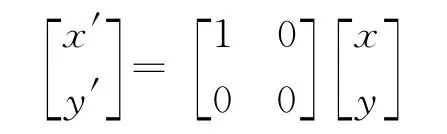
还可以设计更多的类似问题，如旋转变换：

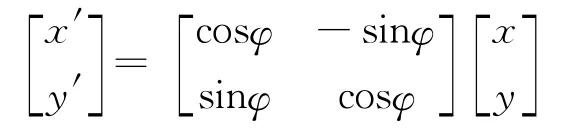
进一步可以推广到更一般的情形：即利用矩阵Am×n，将n维向量转化为m向量（特别是在二维和三维向量之间进行转换，即平面图形和空间图形之间的转换）。

此外，还可以结合一些数学软件（如Matlab）直观再现上述的各种变换，这些应用就把所学的知识变得生动而有趣，这也是 《线性代数》的魅力所在。

4 结语

在线性代数的教学中培养学生的创新意识和创新精神不是一朝一夕的事情，应该有一个比较全面的教学安排，落实到教学的每一个环节。在教学内容的起始处引导学生感悟新概念、新方法与其萌生的背景之间的关联，感受创新意识的激发是内在和外在需要的共同结果；在讲授环节中探究相关知识的创新历程，体会创新思维的某些特征和规律；在应用知识的过程中培养学生创新意识，提高学生解决问题的能力。

［1］同济大学数学系.线性代数 ［M］.北京：高等教育出版社，2007.

［2］李克娥，吴海涛.线性代数 ［M］.武汉：华中科技大学出版社，2013.

［3］张奠宙.微积分教学：从冰冷的美丽到火热的思考 ［J］.高等数学研究，2006（2）：4－6.

［4］蓝洋.吴香艳.电子信息学科中线性代数的教学方法探讨 ［J］.电子设计工程，2012（13）：40－42.