应力三轴度及轧辊凸度对93钨合金板材轧制损伤的影响

王 卺，赵国群，王广春，袁 君

（1山东大学 材料液固结构演变与加工教育部重点实验室，济南250061；2中国兵器工业集团第五三研究所，济南250031）

近年来，我国日益重视稀有金属的开发和利用，金属钨加工技术取得了较大进展，钨合金在国防和民用工业中得到了较广泛应用［1，2］。纯金属钨硬度高、模量高和强度高，其加工和应用具有一定难度［3，4］。93钨合金加入了Ni、Fe等元素，具有相对较好的延展性，故其组织性能、动态力学性能以及加工应用技术成为研究热点之一［5，6］。

93钨合金板材可被广泛应用于制造和加工标准光源、蒸发器皿、电子管栅极、隔热屏、高温炉构件、X射线管钨靶材等产品，但93钨合金板材在轧制过程中容易出现头部分层开裂等缺陷［7］，严重影响其应用。针对钨合金板材轧制成形出现的头部分层开裂缺陷的有关研究目前尚未见报导，也未见针对93钨合金板材轧制过程应力应变分布情况和裂纹产生机理的相关研究。

在板材轧制和成形领域，目前人们对镁合金、铝合金和高强钢等板材成形过程进行了诸多研究，也建立了基于不同破坏准则的损伤演变模型。苌群峰等［8］研究了镁合金板材在温热成形过程中的韧性破坏准则，Poursina等［9］提出了基于遗传算法的钢板冷轧损伤模型，陈志英等［10］研究了GTN细观损伤模型参数对铝合金板料损伤行为的影响规律，给出了损伤参数对铝合金板拉伸成形后板厚减薄率和损伤的影响规律。王在林等［11］研究了韧性断裂准则在超高强钢辊弯成形工艺中的应用，对比了6种常用韧性断裂准则对超高强钢辊弯成形工艺的适用性，宋鸿武［12］等建立了TC11钛合金热变形过程中的损伤演化方程，提出了一种预测宏观裂纹的断裂判定准则，Zhang等［13］预测了镁合金板材轧制过程中的边部裂纹产生过程，建立了相关断裂准则。乔瑞等［14］采用有限元技术分析了钢板的轧制力以及前滑和宽展等参数对轧制过程的影响规律，并给出了应力、应变和温度等场量分布。

综上所述，尽管人们已开展了镁合金、铝合金和高强钢等板材成形过程的损伤模型和断裂机制的研究，但尚未开展对93钨合金板材轧制过程中出现的边裂和头部分层开裂机理的研究。为此，本工作建立了93钨合金板材轧制过程数值模拟模型，重点研究了轧辊凸度对轧制过程中材料应力、应变和断裂损伤的影响规律，探讨了钨合金板材在轧制过程中出现的头部分层开裂的原因。

1 钨合金板轧制过程有限元模型

1.1 轧制模型与本构方程

烧结93钨板尺寸为220mm×100mm×35mm，开坯轧制压下量为30%，采用φ380mm×650mm四辊轧机，轧辊直径为φ650mm，轧制时轧辊固定转速为0.9m／s。轧制温度为1150℃，为简化模拟过程，不考虑传热影响，模具与工件之间的摩擦采用剪切摩擦模型，摩擦因数取值为0.3。在模拟过程中为实现板材正常咬入，在板坯后端加一推板，推动板坯前进，当咬入后再撤销该推板的作用，上、下轧辊转动时通过摩擦带动钨板运动，实现板材厚度减薄轧制，轧制模型如图1所示，其中初始板坯网格为六面体网格，轧制过程中网格畸变后轧坯被再划分为四面体网格。

图1 钨板轧制过程数值模拟模型Fig.1 Numerical simulation model of tungsten sheet rolling process

金属材料的本构模型可分为两类，一类是以Johnson－Cook模型为代表的考虑应变率效应的率相关本构关系，一类为Zerrilli和Armstrong提出的基于微结构的典型体心立方结构金属的本构方程。Zerrilli－Armstrong模型以热激活位错运动理论为框架，描述体心立方结构金属在不同温度和不同应变速率下的本构关系。采用Zerrilli－Armstrong模型进行数值模拟，其本构模型可描述为：

表1 93钨合金 Zerrilli－Armstrong模型参数［16－18］Table1 Zerrilli－Armstrong model parameters of 93 tungsten alloy［16－18］

1.2 辊型曲线

热轧过程中，轧辊凸度由轧辊原始凸度、热凸度和磨损凸度三项组成，主要与弯曲力、剪切力、板材传热产生的弯曲变形和热膨胀有关，此外还需考虑批量生产时的磨损状况。因此，实际生产中的板形由下式确定［16］：

式中：C为实际板形；C0为原始辊型；Cf为受力引起的辊型弯曲；Cw为磨损引起的辊型变化；CT为热传导引起的辊型变化。轧辊与钨板接触会发生弹性压扁，压扁后的轧辊辊型近似抛物线。因此，最终钨板轧制辊型曲线方程为

式中：L0为辊面长度的一半；L为距辊面中心的距离；Cs为辊身中部凸度值。

在轧制过程中，金属板材边缘部位热量散失较中间部位多，板材横向越靠近中部，其温度越高，从而使轧辊因热传导产生的直径膨胀呈现中间部位比两端大，又因热膨胀引起的凸度增加远大于轧辊受力产生的凸度，其结果使轧辊呈现中间凸出形状，但随轧制过程不断进行，磨损量逐渐加大，轧辊凸度也会减小甚至变为负凸度（凹形）。当然，也可根据需求，将轧辊初始凸度设计为较大负凸度，从而使辊型呈现负凸度。为研究不同轧辊凸度对钨板轧制过程的影响规律，设定轧辊为抛物线辊型曲线，其凸度值的范围取为－0.1～0.1mm，图2给出了所选取的轧辊抛物线辊型曲线及其凸度。

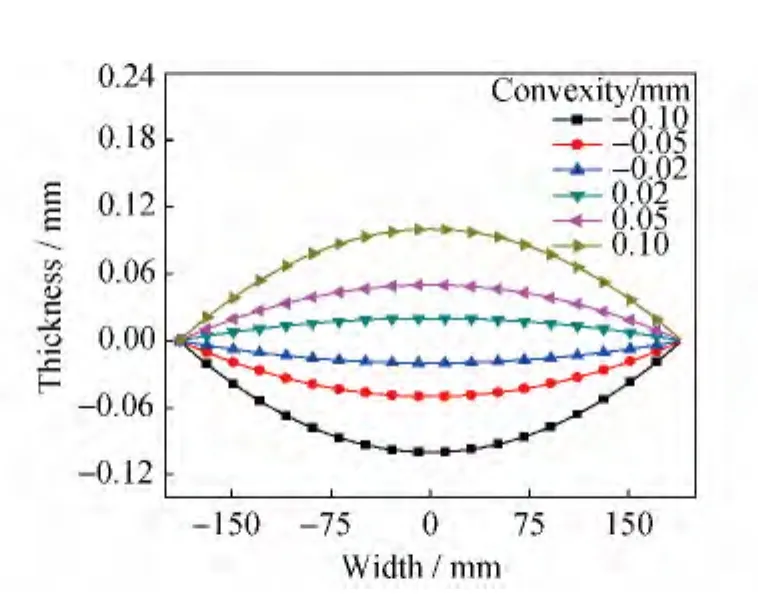
图2 抛物线辊型曲线与轧辊凸度Fig.2 Roller shape parabola curves and roller convexities

2 断裂准则和应力三轴度

金属材料在塑性加工过程中由于大变形引起的材料破坏为塑性破坏，塑性破坏的产生与材料的应力、应变、应变速率、摩擦、孔洞体积分数等有关，断裂准则多采用应力变量沿塑性变形的路径积分形式表示：

式中：F为关于各种应力张量的权函数；σ1为最大主应力；σm为静水压力；为等效应力；n为材料硬化指数；f为断裂时的等效应变；为等效应变；C为断裂阈值或临界破坏值。

Freudenthal认为当单位体积应变能（塑性应变功）达到阈值时，材料即为断裂，该断裂准则可表示为等效应力和等效塑性应变的积分函数

Oyane依据孔洞产生原理，提出了可压缩材料的韧性断裂准则：

式中：a为材料常数；σm／是静水应力与等效应力的比值，记为Rσ，该比值也称为应力三轴度，可用来分析材料的断裂规律。从微观理论方面解释，金属材料的断裂是由微孔洞形核、长大和聚合引起的，因此，应力三轴度可决定孔洞发展和材料的断裂破坏。根据材料断裂时的应力三轴度值可得到材料断裂机制，在低应力三轴度下材料发生剪切断裂，高应力三轴度下发生拉伸断裂，此外，应力三轴度还可反映材料中孔洞在受载条件下的演化情况，在低应力三轴度条件下，孔洞的长大对初始形状敏感［16］。

3 模拟结果与分析

钨板轧制过程中在轧辊压力和摩擦力的同时作用下，厚度方向发生减薄的同时还会沿轧制方向伸长和宽度方向尺寸增大，并且板材厚度方向截面（X－Z面）上的变形、应力以及材料的流动都不均匀。

3.1 轧制板材宽展

轧辊凸度不同对轧后宽展影响不大，只是当轧辊凸度为正值时（凸形轧辊），轧后板材的平均宽度大于其他情况。根据金属变形的最小阻力定律，轧制时金属首先向阻力最小的方向流动，钨板头部和尾部由于受到前、后的变形阻力较小，在宽度方向上金属的延伸变形大于轧件中部金属的延伸变形，使得轧件中部宽度均匀一致，而头部和尾部出现较大变形，尤其是尾部经过前面金属变形的累积，其宽展量明显偏大，轧件上、下表面的金属也因其与轧辊之间的摩擦作用，其宽展量小于内部金属。

通常采用宽展系数来描述轧后板材的宽展情况，其表示为：

式中：W ，w分别为轧前、轧后的板材宽度；H，h分别为轧前、轧后的板材厚度。

根据模拟结果，取轧后板材中间部位宽展基本保持一致的部位，得到图3所示的不同轧辊凸度对轧后板材宽展系数的影响规律，其中横坐标上的1～6表示6种不同的轧辊凸度。当轧辊凸度由负值（凹形辊）逐渐增加到正值（凸形辊）时，轧后板材宽度逐渐增大，因为当轧辊凸度为负值时，轧辊的两端对板材的束缚作用较大，抑制材料横向流动，而当凸度为正值时，轧辊中间凸出部分对板材的挤压占据主要作用，使材料横向流动增加。板材轧后宽展受相对压下量、轧辊直径、摩擦因数和轧前板材宽度等因素影响，较为常用的宽展系数计算公式有赫尔米和亚历山大公式：

比斯公式：

埃尔－凯利和斯帕林公式：

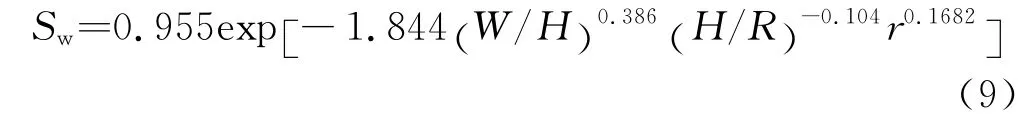
图3中列出了6中不同轧辊凸度和三种经验公式对应的轧制过程宽展系数，三种经验公式得到的结果本身差别较大且与模拟结果也有一定差别，但三种经验公式得到结果的平均值与模拟结果比较吻合。

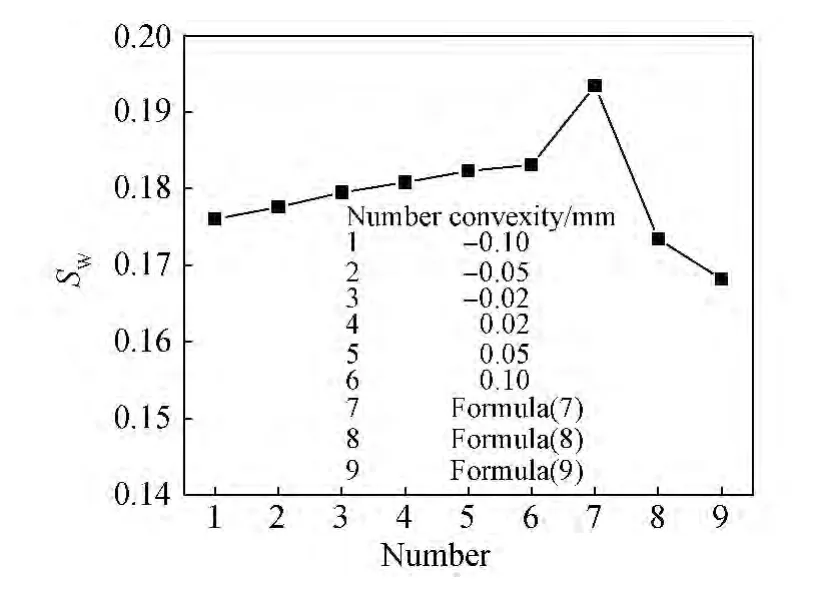
图3 不同凸度轧辊轧制后板材宽展系数SwFig.3 The Swof rolled sheet under different convexities

3.2 轧制载荷与轧制压力分析

轧制过程中随板材的咬入、轧制和推出，轧制载荷从零开始快速增大，达到稳定轧制阶段后，轧制载荷基本保持恒定，在轧制过程结束阶段，轧制载荷又快速下降至零，轧制载荷随轧制时间的变化曲线几乎呈对称状态。图4为稳定轧制阶段不同凸度轧辊条件下轧制压力沿板材横向的分布曲线，在板材横向中间位置，轧制压力最大，其次是板材的边缘部位，轧辊凸度对轧制压力影响不明显。但对稳定轧制阶段不同凸度轧辊条件下的轧制力取平均值，得到图5所示的稳定轧制阶段轧辊凸度与平均轧制力的关系曲线，可见轧辊凸度与平均轧制力存在一定规律，平均轧制力均随凸度值的增加而增加。

图4 不同凸度下正压力沿板材横向分布Fig.4 Distribution of normal pressure along width direction under different convexities

3.3 轧制等效应力、等效应变和应力三轴度分析

截取轧制板材的头部截面（X－Z面），分析该截面Mises屈服准则下的等效应力、等效应变情况。当轧辊凸度由－0.1mm增至0.1mm时，头部截面（X－Z）面的等效应力和等效应变的变化并不明显，因此只选取轧辊凸度值为－0.1mm的情况进行分析。图6和图7分别给出了凸度值为－0.1mm时对应的该截面上的等效应变和等效应力分布情况。从图6可看出，等效应变和等效应力在截面的边角和中心部位较大。分析材料产生破坏的韧性断裂准则多是与塑性变形时的应力、应变及相关常数有关的函数，尽管从图6和图7中不易明显确定轧辊凸度与裂纹产生的关系，但可确定板材头部在咬入过程中容易产生裂纹的部位。

图5 稳定轧制阶段轧辊凸度与平均轧制力Fig.5 Roller convexity and mean rolling load in the stable rolling stage

图6 轧辊凸度为－0.05mm头部截面等效应变Fig.6 Effective strain of the head section in－0.05mm roller convexity

图7 轧辊凸度为－0.05mm头部截面等效应力Fig.7 Effective stress of the head section in－0.05mm roller convexity

图8为轧辊凸度为－0.1mm时咬入阶段板材头部截面厚度方向中心线位置的应力三轴度变化过程，在板材头部刚刚与轧辊接触时，应力三轴度值小于0，且中间部位的数值绝对值较两侧大，随板材逐渐咬入，应力三轴度由负值逐渐增大到正值，且中间部位的数值明显增大。由断裂力学可知，应力三轴度数值的正负表示材料的受载情况，当受到拉伸作用时其值为正，受压缩作用时其值为负。轧制过程中板材主要受轧辊压力和摩擦力作用，其中压力作用方向垂直于接触面，摩擦力则沿接触面方向。

图8 －0.1mm凸度轧辊咬入阶段应力三轴度变化过程Fig.8 Triaxiality change process in the bite stage for convexity of－0.1mm

图9为不同模拟步数时在不同凸度轧辊条件下轧制板材头部截面高度方向中心线上应力三轴度Rσ的分布变化情况，从轧制板材宽度边缘至中心位置，应力三轴度的值逐渐增加，并在宽度中心部位达到最大值。对于轧辊凸度绝对值较大的情况，图9（a），（b）表明在钨板头部材料开始和轧辊接触时，其受到的压应力作用较大，这使得板材咬入较为困难；图9（c）表示当头部材料完全进入辊缝后，轧辊凸度为－0.1，－0.05mm和0.1mm时所对应的应力三轴度曲线偏高，而轧辊凸度为－0.02，0.02mm和0.05mm对应的应力三轴度曲线偏低；随着咬入的进行，这种趋势更加明显，如图9（d）所示。这与应力分析结果一致，即在板材头部中间部位发生开裂主要是由于拉应力的作用而引起的，而这种拉应力是由于材料变形不均匀所致，即板材宽度方向两端材料流动较中间部位大，对中间区域的材料产生拉伸作用，因此，当轧辊凸度较大时，这种材料流动的不均匀性也随之增大，Rσ值也相对较大，从而产生裂纹的倾向性就大。

图9 不同轧辊凸度下应力三轴度的变化过程（a）第12步；（b）第22步；（c）第32步；（d）第36步Fig.9 Triaxiality change process under different convexities（a）step12；（b）step 22；（c）step 32；（d）step 36

取靠近头部截面中间的点P，其位置如图10所示。图10分析了该点在轧制过程中的主应力状态变化，咬入阶段开始时，P点主要受轧辊的压应力σ3作用，随着板材不断进入辊缝，当模拟步数达到30后，板材头部逐渐与轧辊脱离接触，P点变为受三向拉应力作用，易造成P点处开裂。图11为实际钨板轧制件的头部开裂情况，整个轧件头部在板材厚度中心部位沿宽度方向整体开裂，这与图10所示的P点的主应力在轧制过程中的分布相一致。

图10 －0.1mm凸度轧辊咬入阶段P点主应力变化（a）P点位置；（b）P点主应力变化Fig.10 Change of point P’s principal stress in the bite stage under convexity of－0.1mm（a）position of point P；（b）change of point P’s principal stress

图11 轧制钨板头部开裂Fig.11 Crack in the rolled tungsten head

4 结论

（1）轧辊凸度由负值－0.1mm增加到正值0.1mm，对金属材料向宽度方向流动的挤压作用逐渐增强，宽展系数也随之逐渐增大，由0.17上升到0.19，与之相对应轧制力也呈递增趋势，稳定阶段的平均轧制力由1.7×106N增加到1.8×106N。

（2）钨板轧制头部开裂是由于咬入过程中板材头部材料流动不均，尤其对于难熔金属，其加工塑性差且加工温度较高，当材料的变形引起等效应变分布不均时，中间部分材料受到三向拉应力作用产生开裂，是由头部中间部位向两侧撕裂开造成的材料破坏。

（3）当轧辊凸度值为－0.02，0.02mm和0.05mm时，材料流动均匀性相对较好，头部开裂部位应力三轴度相对较小，当凸度为正值0.02mm和0.05mm时，应力三轴度要小于负凸度情况。

［1］马运柱，张佳佳，刘文胜，等.真空热处理对微波烧结93W－Ni－Fe合金显微组织及力学性能的影响［J］.稀有金属材料与工程，2012，41（9）：1680－1683.MA Yun－zhu，ZHANG Jia－jia，LIU Wen－sheng，et al.Effects of vacuum heat treatment on microstructure and mechanical properties of 93W－Ni－Fe alloy by microwave sintering［J］.Rare Metal Materials and Engineering，2012，41（9）：1680－1683.

［2］刘海燕，宋卫东，栗建桥.钨合金动态力学性能的三维数值模拟研究［J］.材料工程，2012，（6）：71－75.LIU Hai－yan，SONG Wei－dong，LI Jian－qiao.Three dimensional numerical analysis on dynamic mechanical property of tungsten alloys［J］.Journal of Materials Engineering，2012，（6）：71－75.

［3］詹土生，周智耀，孙远，等.塑性变形对钨铜板材显微结构及性能的影响［J］.稀有金属材料与工程，2010，39（6）：1053－1056.ZHAN Tu－sheng，ZHOU Zhi－yao，SUN Yuan，et al.Influence of plastic deformation on microstructure and performance of 85W－Cu sheet［J］.Rare Metal Materials and Engineering，2010，39（6）：1053－1056.

［4］DAS J，RAO G A，PABI S K，et al，Deformation behavior of a newer tungsten heavy alloy［J］.Materials Science and Engineering：A，2011，528（19）：6235－6247.

［5］刘强强，池成忠，许树勤，等.轧制变形率对钨板晶粒尺寸与硬度的影响［J］.锻压装备与制造技术，2012，（1）：98－100.LIU Qiang－qiang，CHI Cheng－zhong，XU Shu－qin，et al.Experimental study of rolling process for medium and heavy molybdenum plate［J］.China Metalforming Equipment and Manufacturing Technology，2012，（1）：98－100.

［6］MA Hong－lei，HU Geng－kai，TAN Cheng－wen，et al.Damage mechanisms for 93Wand 97Wtungsten－based alloys［J］.Rare Metal Materials and Engineering，2010，39（8）：1344－1347.

［7］闫玉曦，孙权，陈建钧，等.基于GTN模型的冷轧硅钢边部裂纹扩展研究［J］.机械工程学报，2012，48（10）：33－39.YAN Yu－xi，SUN Quan，CHEN Jian－jun，et al.Analysis for the propagation of edge crack of silicon steel during cold rolling process based on GTN damage model［J］.Journal of Mechanical Engineering，2012，48（10）：33－39.

［8］苌群峰，彭颖红，杜朝辉.镁合金板材温热成形韧性破裂准则［J］.机械工程学报，2009，45（10）：294－299.CHANG Qun－feng，PENG Ying－hong，DU Zhao－hui.Ductile fracture criterion for warm deep drawing of magnesium alloy sheet［J］.Journal of Mechanical Engineering，2009，45（10）：294－299.

［9］POURSINA M，DEHKORDI N T，FATTAHI A，et al.Application of genetic algorithms to optimization of rolling schedules based on damage mechanics［J］.Simulation Modeling Practice and Theory，2012，22（3）：61－73.

［10］陈志英，董湘怀.GTN细观损伤模型参数对板料损伤行为的影响［J］.锻压技术，2012，37（3）：23－27.CHEN Zhi－ying，DONG Xiang－huai.Influence of GTN mesodamage model parameters on sheet forming damage behavior［J］.Forming and Stamping Technology，2012，37（3）：23－27.

［11］王在林，韩飞，刘继英，等.韧性断裂准则在超高强钢辊弯成形工艺中的应用［J］.塑性工程学报，2012，19（4）：16－20.WANG Zai－lin，HAN Fei，LIU Ji－ying，et al.Research on application of ductile fracture criteria in roll forming process of ultra high strength steel［J］.Journal of Plasticity Engineering，2012，19（4）：16－20.

［12］宋鸿武，张士宏，程明，等.钛合金热变形过程中裂纹缺陷的预测［J］.稀有金属材料与工程，2012，41（5）：781－785.SONG Hong－wu，ZHANG Shi－hong，CHENG Ming，et al.Fracture prediction during hot deformation process of a titanium alloy［J］.Rare Metal Materials and Engineering，2012，41（5）：781－785.

［13］ZHANG D F，DAI Q W，FANG L，et al.Prediction of edge cracks and plastic－damage analysis of Mg alloy sheet in rolling［J］.Transactions of Nonferrous Metals Society of China，2011，21（5）：1112－1117.

［14］乔瑞，王长松，盛桂伟.板材轧制过程的三维有限元分析［J］.冶金自动化，2005，（增刊）：230－233.QIAO Rui，WANG Chang－song，SHENG Gui－wei.Three dimensional analysis of the sheet’s rolling process［J］.Metallurgical Industry Automation，2005，（Suppl）：230－233.

［15］李频，温方金，杨雁青，等.3000mm中板轧机辊型预测模型研究及应用［J］.钢铁研究学报，2011，（增刊）：67－71.LI Pin，WEN Fang－jin，YANG Yan－qing，et al.Roll contour model of 3000mm plate mill and its application［J］.Journal of I－ron and Steel Research，2011，（Suppl）：67－71.

［16］RAMESH K T，LENNON A M，The thermo－visco plastic response of polycrystalline tungsten in compression［J］.Materials Science and Engineering：A，2000，276（9）：9－21.

［17］肖松涛，周廉，王国栋，等.钨塑性变形抗力数学模型的研究［J］.稀有金属快报，2004，23（11）：26－28.XIAO Song－tao，ZHOU Lian，WANG Guo－dong，et al.Analysis on plastic deformation resistance of mathematical model of tungsten［J］.Rare Metals Letters，2004，23（11）：26－28.

［18］徐英鸽，康进兴，陈文涛，等.93WNiFe合金抗拉强度的温度效应［J］.材料热处理学报，2006，35（14）：1－3.XU Ying－ge，KANG Jin－xing，CHEN Wen－tao，et al.Temperature effects on strength of 93WNiFe alloy ［J］.Transactions of Materials and Heat Treatment，2006，35（14）：1－3.