2.25Cr－1Mo钢后续热处理中的磷偏聚行为

张喜亮，刘 涛，崔国华，周昌玉，刘 争，张 维

（1河北工程大学 装备制造学院，河北 邯郸056038；2南京工业大学 机械与动力工程学院，南京210009）

2.25Cr－1Mo低合金结构钢具有较高强度和抗氧化性以及良好的焊接性而广泛应用于压力容器、热电站锅炉、汽车、核能和飞机发动机金属构件等场合，然而，该钢在高温条件下长期工作时，其中的某些微量合金元素或杂质元素会偏聚到晶界处导致材料变脆，即出现回火脆性现象［1－3］。

合金元素在晶界上的偏聚对工程材料的力学性能有着深刻的影响，多年来一直备受冶金和材料学者的关注［4－6］。研究者们在实验过程中发现，对于已脆化一定程度的材质，在后续热处理过程中难以进一步脆化甚至发生脱脆现象，如Doucet［7］将已脆化的2.25Cr－1Mo钢进行步冷实验企图获得进一步的脆化，但未取得成功。谈金祝和黄文龙［8］对运行5年的加氢反应器随炉试样进行回火处理，结果不但没有达到预期目标，反而使材料发生脱脆。这些现象目前仍未得到合理的解释，本工作以运行12年加氢反应器随炉试样2.25Cr－1Mo钢作为研究对象，对晶界偏聚理论进行深化和扩展，并结合俄歇电子能谱分析方法从机理上对这一问题进行分析，揭示2.25Cr－1Mo钢材质脆化和脱脆的本质。

1 2.25Cr－1Mo钢材质脆化及脱脆机理

合金材料2.25Cr－1Mo钢的回火脆化是由于P，As，Sb，Sn等杂质原子在晶界偏聚所致，其中P原子的晶界偏聚是引起回火脆化的主要因素［9，10］。20世纪50年代，Mclean借助统计热力学理论给出了晶界偏聚热力学与动力学公式［11］：

式中：Cg为P原子在晶内的平均浓度，用原子分数表示（%）；A为常数；k为波尔兹曼常数（J·K－1）；T为绝对温度（K）；ΔG为偏聚自由能（kJ／mol）；Cgb（t）为P原子在t时间内的晶界浓度（%）；Cgb∞为P原子在达到平衡时的晶界浓度（%）；Cgb0为P原子在初始状态时的晶界浓度（%）；Dp为P原子的扩散系数（m2·s－1）；α为富集比；d为晶界宽度（m）；erfc为补余误差函数，由下式决定：

根据平衡晶界偏聚理论，首先计算不同温度不同运行时间下磷原子的晶界偏聚量，然后以时间为横坐标，磷原子的晶界偏聚量为纵坐标，把不同温度下的相同偏聚量用曲线连接起来即可获得磷的等晶界偏聚量曲线。本工作以随加氢反应器一起运行的试样2.25Cr－1Mo钢为研究对象，其化学成分如表1所示，计算求得的等晶界偏聚量曲线见图1，所需参数见表2。

表1 2.25Cr－1Mo钢化学成分（质量分数／%）Table1 Chemical composition of 2.25Cr－1Mo steel（mass fraction／%）

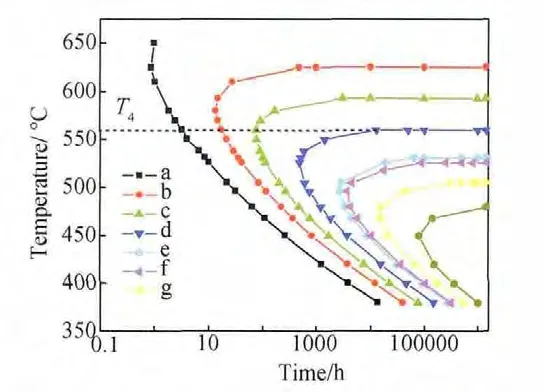
图1 2.25Cr－1Mo钢中磷的等晶界偏聚量曲线Fig.1 The same grain boundary segregation of phosphorusconcentration curve in 2.25Cr－1Mo steel

图1中每条C形曲线上，P原子晶界偏聚浓度大小相等，即材料的脆化程度相同。图1中a～g曲线所代表的磷原子晶界偏聚浓度值大小如表3所示。

根据图1中的曲线关系及表3中的数据可知：对任一时间，每条等脆化曲线可有两个相应的温度，即与C曲线下端斜线相交温度和上端平坦线相交温度。后者表示该温度下P原子在晶界上的偏聚量趋于饱和，材料不会进一步加深脆化；当后续热处理温度超过当前饱和偏聚量下的温度，等温脆化曲线左移，P原子的晶界偏聚浓度降低，材质表现为脱脆；当后续热处理温度低于当前饱和偏聚量下的温度时，等温脆化曲线右移，P原子的晶界偏聚浓度增大，材质表现为进一步脆化；本文定义每条等脆化曲线的上端平坦线对应的温度为此脆化度下的“临界脆化温度”。2.25Cr－1Mo钢的每一脆化度都有一临界脆化温度与之对应，以图1中的曲线d为例，其对应的临界脆化温度为T4，则在后续热处理过程中，若该热处理的温度高于T4，此热处理过程为脱脆过程，反之为脆化过程。

表2 理论计算参数［12，13］Table2 Parameters for theoretical calculation［12，13］

表3 原子P晶界偏聚量（原子分数／%）Table3 The grain boundary segregation concentration of element P（atom fraction／%）

利用公式（1）和公式（2）求取不同温度下P原子的晶界偏聚量及各温度下P原子最大平衡晶界偏聚量与运行温度关系，结果如图2所示，其中B曲线表示P原子晶界最大偏聚浓度与运行温度之间的关系，C曲线为P原子达到最大晶界偏聚浓度99.999%的时间与运行温度的关系。由B曲线可知，在回火温度范围内，对于任一温度，都有一个最大P原子晶界偏聚浓度与之对应，且温度越高，达到平衡时P原子晶界偏聚量越低；C曲线表明温度越高，偏聚速率越快，即达到最大晶界偏聚量的时间越短。根据B曲线可以求取任意脆化度下的临界脆化温度，对于运行12年的加氢反应器母材2.25Cr－1Mo钢而言，前期的实验结果表明P原子晶界偏聚浓度为14.86%［14］，由图2可知，其临界脆化温度为505℃，此结果已被作者前期的实验所证实［15，16］。

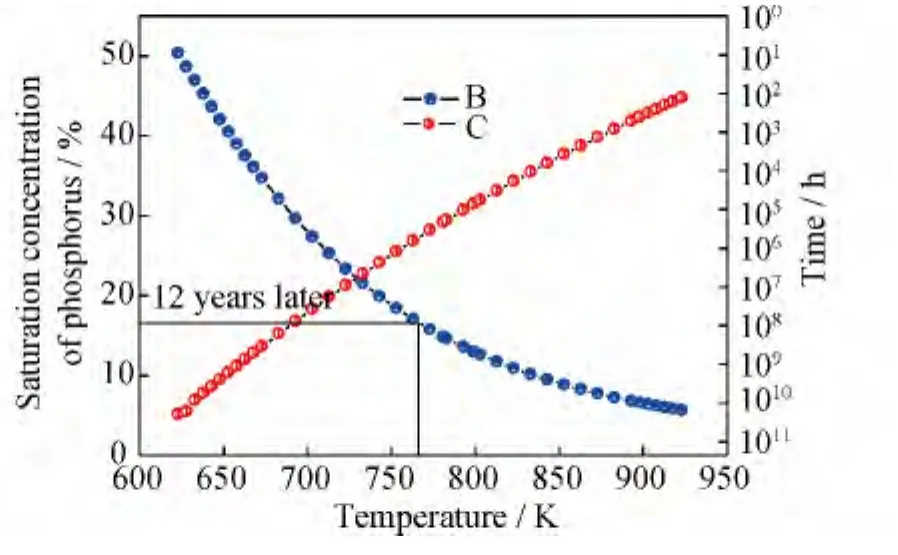
图2 P原子平衡晶界偏聚量、平衡时间与运行温度的关系Fig.2 Relationship between saturation concentration of phosphorus vs saturation time and holding temperature

2 已脆化2.25Cr－1Mo钢的脱脆模型

为获得杂质原子P晶界反偏聚量与时间的关系，本文进行如下假设：由于晶粒尺寸远大于晶界尺寸，因而假设晶粒为一个半无限大固体，晶界为一个有限大固体，如图3所示；假设原子P由晶界向晶内扩散时，其扩散系数不随晶界及晶内杂质浓度的变化而变化；假设原子P的扩散系数不受其他元素的影响，即不考虑钢中合金元素或其他杂质对P原子的影响；杂质原子P在晶内的平均浓度不随晶界上杂质的偏聚而变化。

由Fick第一定律和第二定律［17］：

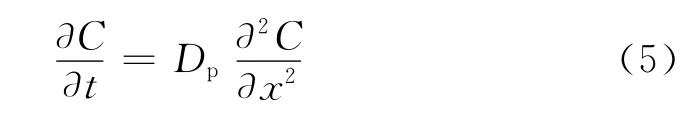
式中：Dp是原子P的扩散系数；C为原子P在晶界上的浓度。

根据物质守恒定律：单位时间内通过单位晶界面积的杂质原子的量等于该杂质原子在晶界内的减少量，即：

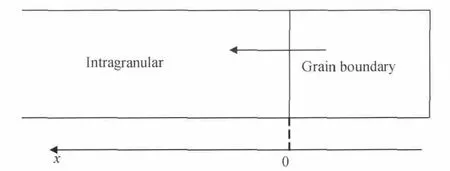
图3 杂质原子P由晶界向晶内偏析模型Fig.3 Model for segregate of impurity P from grain boundary to intracrystalline

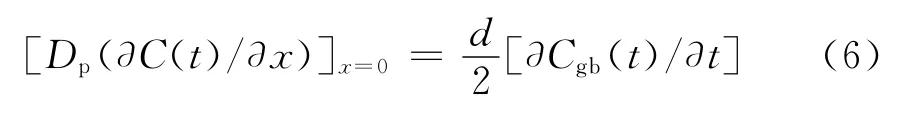
式中：d为晶界宽度；“1／2”的含义为晶界内的原子P是向晶界两侧晶粒内扩散的。

在晶粒与晶界交接面上（x＝0），原子P的浓度C（t）为：

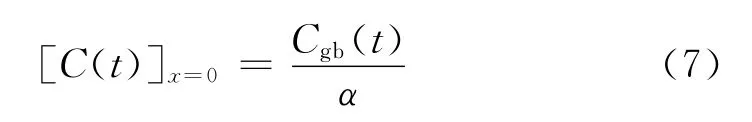
为解偏微分方程式（5）和式（6），引用拉普拉斯变换［18］，令：

式中P为拉普拉斯变换参数，且足够大能保证积分收敛。则式（5）转换为：

式（9）和式（10）中，q2＝p／Dp，M为积分常数。按拉普拉斯变换，将（6）式变换为：

将式（10）代入式（11）得：

将（12）式代入（10）式得到：

按拉普拉斯转换表［18］，对（13）式转换，其中（8）式中C为：

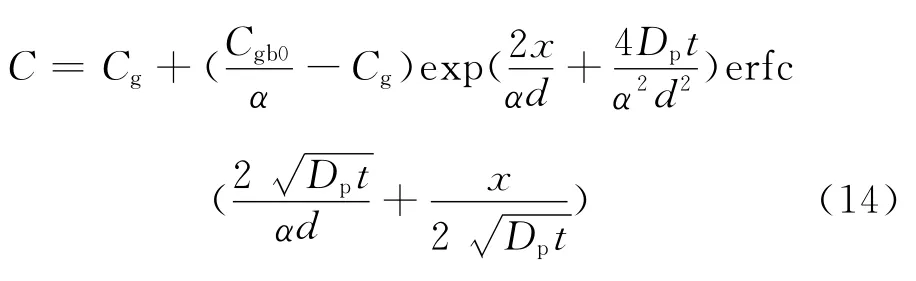
当x＝0时，（14）式经变换得到原子P晶界反偏聚量与运行时间的关系式：

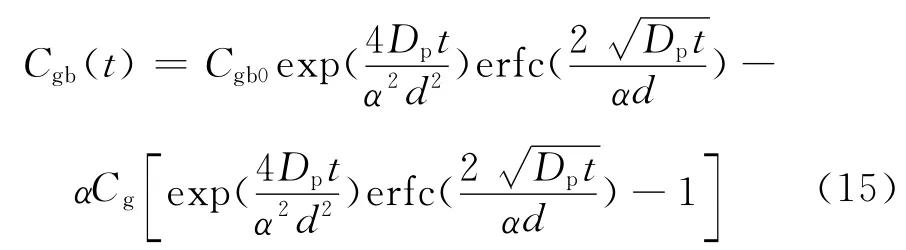
式中：Cgb（t）为原子P在t时间内晶界浓度；Cgb0为已脆化材质在保温前P原子的晶界偏聚浓度；Cg为原子P初始晶内浓度。

3 2.25Cr－1Mo钢脱脆模型的实验验证

3.1 实验

以随加氢反应器运行12年的2.25Cr－1Mo钢作为实验材料，经设计切割共分成5组，编号分别为T1，T2，T3，T4，T5；脱脆热处理实验：由图2计算可知，运行12年的试样其临界脆化温度为505℃，根据本文理论，高于此温度的后续热处理为脱脆过程，且温度越高，脱脆速率越快。经综合考虑，本文选择的脱脆温度为538℃，试样T1～T5保温时间分别为0.5，5，10，30，60h。具体的热处理实验过程为：首先以50℃／h从室温加热到538℃，保温t小时后空冷至室温；Auger电子能谱实验：脱脆处理后的试样加工成标准俄歇试样，在俄歇装置内液氮冷却1h后打断，取沿晶断口12～15点测量P原子晶界浓度，其平均值作为实验结果。Auger电子能谱实验是在PERKIN－ELEMER PHI595装置内完成的。

3.2 实验结果分析

应用本文推导的脱脆模型（15）式对上述实验过程进行计算模拟，所需参数见表2，其中Cgb0取14.86%，Dp为0.4×10－18m2／s，具体理论计算结果与实验结果及误差分析如表4及图4所示，俄歇电子能谱图见图5，断口形貌见图6。

表4 理论计算与实验结果Table4 Theoretical calculations and experiment results

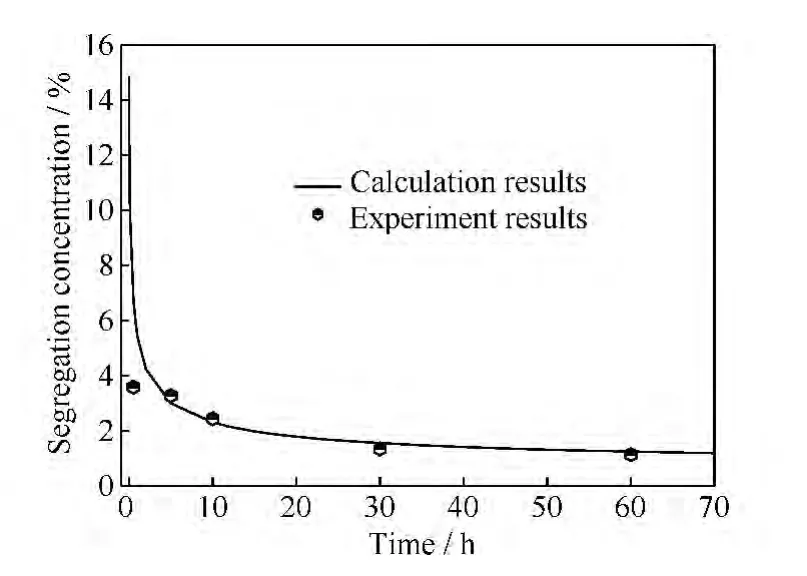
图4 运行12年的2.25Cr－1Mo钢P原子晶界偏聚浓度的理论计算与实验结果关系Fig.4 Relationship between theoretical calculations and experiment results of grain boundary segregation concentration of phosphorus for 2.25Cr－1Mo steel served for 12years

图5 试样T1（a）和T2（b）的Auger电子能谱图Fig.5 Auger electron spectra of specimen T1（a）and T2（b）

根据表4和图4，对于运行12年的2.25Cr－1Mo钢，在538℃下分别保温0.5，5，10，30，60h后，P原子的晶界浓度由14.86%分别降低至3.58%，3.27%，2.43%，1.34%，1.13%，推导模型计算结果与实验结果除第一点其余皆较为吻合，误差分别为87.7%，8.56%，5.34%，15.67%，9.73%。第一点误差较大的原因：根据图4，对于运行12年的加氢反应器母材，在538℃下进行脱脆处理，随着保温时间的增加，晶界上P原子的浓度不断降低，在脱脆过程中的前3h，P原子反偏聚速率较大，即晶界上P原子的浓度急剧降低，特别是在脱脆过程中的前1h，晶界上原子P的浓度会随着保温时间的小幅度波动而产生较大的变化值。脱脆过程中需要从室温升温至538℃，升温阶段需10h左右，然后再保温，对于T1组试样，由于其保温时间较短，且落在了反偏聚速率最快的阶段，因此该点上理论计算的结果与实验结果误差较大。

图6 俄歇试样的断口形貌Fig.6 Fracture morphology for Auger electron spectra specimens

4 讨论

本工作利用平衡晶界偏聚理论计算了加氢反应器母材2.25Cr－Mo钢在服役条件下P原子晶界偏聚量并通过实验进行验证，利用推导的脱脆模型对服役12年的2.25Cr－Mo钢在后续热处理过程中P原子晶界偏聚情况进行预测，结果如图7所示。

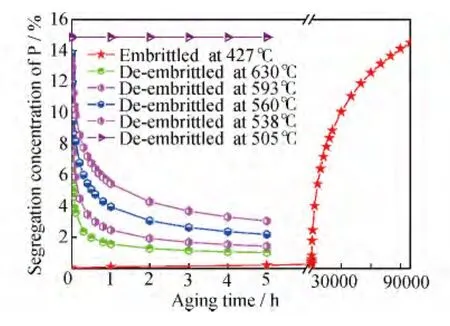
图7 运行12年加氢反应器母材2.25Cr－1Mo钢脆化与脱脆过程Fig.7 The embrittled and de－embrittled process for 2.25Cr－1Mo steel after 12years

由图7可见，服役12年的2.25Cr－1Mo钢，高于其临界脆化温度的后续热处理，原子P在晶界上的浓度降低，材质发生脱脆，随着保温时间的延长，脱脆程度逐渐增大；在脱脆初期，原子P在晶界的浓度降低速率较快，而随着时间的延长逐渐趋于平缓。此外，由图7还可知，高于临界脆化温度的后续热处理，随着保温温度的提高，P原子由晶界向晶内偏聚的速率越快，即在相同的时间内温度提高脱脆程度越大；与脆化过程相比，材质的脱脆速率远大于脆化速率，对于运行12年的2.25Cr－1Mo钢，在538℃下保温5h（高于其临界脆化温度），P原子的晶界浓度由14.86%降低至2.99%，降低量达79.8%。而在630℃下保温2h，P原子的晶界浓度降低至1.27%，从材质脆化角度分析，基本恢复到使用前的状态，这一结果可为2.25Cr－1Mo钢的延寿技术提供一定的理论支撑。

5 结论

（1）已脆化的2.25Cr－1Mo钢存在临界脆化温度，高于此温度的后续热处理为脱脆过程，反之为脆化过程。

（2）随2.25Cr－1Mo钢脆化程度的增大，其等脆化曲线逐渐向低温长时间方向移动，服役12年2.25Cr－1Mo钢的临界脆化温度为505℃。

（3）已脆化的2.25Cr－1Mo钢，后续热处理温度越高（该温度高于临界脆化温度），脱脆程度越大，所需的脱脆时间越短；在脱脆初期，P原子在晶界的浓度降低速率较快，而随着时间的延长逐渐趋于平缓。

（4）2.25Cr－1Mo钢的脱脆速率远大于脆化速率，以随加氢反应器运行12年的试块为例，高于临界脆化温度数小时的保温即可消除脆化现象，这为将来延寿技术提供了一定的理论支撑。

［1］ENOMOTO M，MARUYAMA N，WU K M，et al.Alloying element accumulation at austenite boundaries below the time－temperature－transformation diagram bay in an Fe－C－Mo alloy［J］.Materials Science and Engineering A，2003，343（2）：151－157.

［2］SONG S H，WENG L Q.An FEGSTEM study of grain boundary segregation of phosphorus during quenching in a 2.25Cr－1Mo steel［J］.Journal of Materials Science and Technology，2005，21（4）：445－450.

［3］袁泽喜，万涛，刘静.中温大变形量下磷在2.25Cr－1Mo钢中的晶界偏聚［J］.武汉科技大学学报：自然科学版，2008，31（3）：299－303.YUAN Ze－xi，WAN Tao，LIU Jing.Moderate temperature and great deformation－induced grain boundary segregation of phosphorus in 2.25Cr1Mo steel［J］.Journal of Wuhan University of Science and Technology：Natural Science Edition，2008，31（3）：299－303.

［4］王晓，王作成，王协彬，等.亚温淬火对硼镍添加含铌低合金高强度 H 型钢组织性能的影响［J］.材料工程，2012，（3）：22－27.WANG Xiao，WANG Zuo－cheng，WANG Xie－bin，et al.Effect of subcritical quenching on microstructures and mechanical properties of boron－nickel added Nb－treated HSLA H－beam［J］.Journal of Materials Engineering，2012，（3）：22－27.

［5］赵红霞，黄旭，王宝，等.热处理对Ti－35V－15Cr－0.15Si－0.05C合金热稳定性能的影响［J］.材料工程，2013，（7）：73－77.ZHAO Hong－xia，HUANG Xu，WANG Bao，et al.Effect of heat－treatment on the microstructure and thermal stability properties of Ti－35V－15Cr－0.15Si－0.05Ctitanium alloy［J］.Journal of Materials Engineering，2013，（7）：73－77.

［6］SONG S H，WU J，WANG D Y，et al.Stress－induced non－equilibrium grain boundary segregation of phosphorus in a Cr－Mo low alloy steel［J］.Materials Science and Engineering：A，2006，430（1）：320－325.

［7］DOUCET A B.Effects of service exposure of 2 1／4CR pressure vessel steel in a heavy oil hydrocracker［A］.Firness－in－Service and Decisions for Petroleum and Chemical Equipment［C］.New York：ASME，1995.407－412.

［8］谈金祝，黄文龙.步冷试验法预测2.25Cr－1Mo钢回火脆性［J］.南京化工大学学报，1998，20（12）：17－20.TAN J Z，HUANG W L.Application of step－cooling test method for temper embrittlement of 2.25Cr－1Mo steel［J］.Journal of Nanjing University of Chemical Technology，1998，20（12）：17－20.

［9］吴平，贺信莱，于栋友，等.晶界非平衡偏聚的发生与发展过程［J］.金属学报，2002，38（1）：6－10.WU Ping，HE Xin－lai，YU Dong－you，et al.Evolution of non－equilibrium segregation of boron on grain boundaries［J］.Acta MetallurGica Sinica，2002，38（1）：6－10.

［10］陈贤淼，宋申华.高温塑性变形引起的P非平衡晶界偏聚［J］.物理学报，2009，58（1）：72－76.CHEN Xian－miao，SONG Shen－hua.Non－equilibrium grain boundary segregation of phosphorous during high temperature plastic deformation［J］.Acta Physica Sinica，2009，58（1）：72－76.

［11］MCLEAN D.Grain Boundaries in Metals［M］.London：Oxford University Press，1957.

［12］张喜亮，周昌玉，张国栋.基于平衡晶界偏聚理论的步冷实验脆化机理研究［J］.材料热处理学报，2008，29（1）：167－170.ZHANG Xi－liang，ZHOU Chang－yu，ZHANG Guo－dong.Study on mechanism of temper embrittlement for step－cooling test based on the theory of equilibrium grain boundary segregation［J］.Transactions of Materials and Heat Treatment，2008，29（1）：167－170.

［13］李庆芬，李莉，金国，等.磷的非平衡晶界偏聚恒温动力学实验及计算研究［J］.哈尔滨工程大学学报，2004，25（2）：141－146.LI Qing－fen，LI Li，JIN Guo，et al.Experimental study on nonequilibrium grain－boundary segregation isothermal kinetics of phosphorus and kinetics calculation［J］.Journal of Harbin Engineering University，2004，25（2）：141－146.

［14］谈金祝.Auger电子能谱分析方法及其在2.25Cr－1Mo钢回火脆性中的应用［J］.南京工业大学学报，2003，25（1）：73－76.TAN Jin－zhu.Method of electron spectroscopy analysis and its application as for temper embrittlement of 2.25Cr－1Mo steels［J］.Journal of Nanjing University of Technology，2003，25（1）：73－76.

［15］张喜亮，周昌玉.2.25Cr－1Mo钢基于平衡晶界偏聚理论的连续脆化机理研究［J］.材料热处理学报，2009，30（4）：194－197.ZHANG Xi－liang，ZHOU Chang－yu.Study on further embrittlement mechanism in 2.25Cr－1Mo steel based on theory of equilibrium grain boundary segregation［J］.Transactions of Materials and Heat Treatment，2009，30（4）：194－197.

［16］ZHANG X L，ZHOU C Y.Study on the mechanism of embrittlement and de－embrittlement for 2.25Cr－1Mo steel［J］.Journal of Iron and Steel Research International，2011，18（3）：47－51.

［17］CRANK J.The Mathematics of Diffusion［M］.Oxfords：Clarendon Press，1956.

［18］CARSAW H S.Conduction of Heat in Solids［M］.Oxfords：Clarendon Press，1959.