搅拌摩擦焊接全过程热力耦合有限元模型

崔俊华，柯黎明，刘文龙，郭正华，赵刚要，方 平

（1西北工业大学 材料学院 摩擦焊接陕西省重点实验室，西安710072；2南昌航空大学轻合金加工科学与技术国防重点学科实验室，南昌330063）

搅拌摩擦焊接（Friction Stir Welding，FSW）是由英国焊接研究所THOMAS等［1］于1991年发明的一种新型固相连接技术。FSW克服了熔焊时产生的诸如气孔、裂纹、大变形等缺陷，以优质、高效、节能和无污染的特点广泛应用于航空、航天以及汽车等领域。由于FSW过程是一个温度变化、组织结构转变、应力应变和金属流动等方面相互耦合、共同作用的复杂过程，单纯采用理论解析和实验方法难以准确、有效地解决FSW的实际问题，特别是FSW过程温度场和焊缝金属塑性流动行为的研究。有限元模拟技术以良好的可视化和过程再现性优点，已成为国内外FSW研究的趋势。Schmidt等［2］基于ABAQUS／Explicit建立了完全热力耦合动态分析模型，该模型能够模拟热力条件下的稳定焊接阶段。Xu等［3］将FSW看成稳态过程，采用ALE技术与预设温度场方式建立了FSW稳定焊接阶段热力耦合模型。张昭等［4］基于ALE技术建立了6061－T6铝合金焊接构件FSW稳定焊接阶段完全热力耦合模型。鄢东洋等［5］采用引入热源模型的解析方法，建立了FSW稳定焊接阶段分析模型。Guo等［6］基于ALE技术建立了FSW过程的稳定焊接阶段热力耦合模型。由于无法克服网格高度畸变问题，而采用预先在焊件上设置通孔的处理方式，仅能实现稳定焊接阶段的仿真分析。上述处理方式导致稳定焊接阶段初始时刻的温度场和塑性变形场与实际情况不符，且因搅拌头端部热力条件发生了改变，使得模拟结果无法真实反映搅拌头端部周围的温度场、塑性变形场和材料的流动行为。FSW初始阶段产热是FSW过程进入稳定焊接的基础和关键，在建立搅拌摩擦焊接过程模型中不应被忽略。Mandal等［7］基于ABAQUS／Explicit建立了FSW 下压阶段的热力耦合有限元模型。Hamilton等［8］和Yu等［9］基于ABAQUS／Explicit尝试建立FSW 全过程的热力耦合模型，但两者模型获得的温度场和塑性变形场与实验研究的结果出入较大，其中后者所建模型无法预测应力场和塑性变形场。

基于FSW过程有限元模型对焊接过程研究的重要性，以及现有有限元模型的缺陷，为更准确地反映FSW过程的温度场和塑性变形情况，本工作在ABAQUS软件平台上建立搅拌摩擦焊接全过程（下压阶段和稳定焊接阶段）热力耦合有限元模型，基于ALE网格自适应技术对网格及边界条件进行合适处理，解决了焊接过程中网格高度畸变问题。模拟分析了6061铝合金焊件焊接过程温度场和材料塑性变形场，并与实验进行对比。

1 有限元模型

1.1 几何模型

焊接构件为40mm×40mm×3mm的完整板材，搅拌针端部直径6mm，锥角20°，轴肩直径18mm，轴肩表面带有1.5°的凹角，边缘处有半径为0.5mm的倒圆角。在有限元模型中搅拌头设定为解析刚体，如图1所示。

1.2 材料定义

采用Johnson－Cook本构模型［10］描述FSW 过程中局部高温、高速、高压的大变形和高应变速率下材料的热力学行为（式（1））。采用6061铝合金［4，11］材料焊接构件验证模型，其相关参数如表1所示。

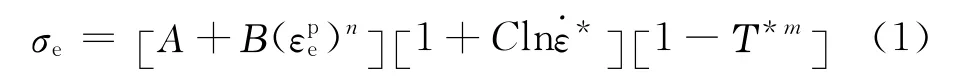
式中：σe为Von Mises流动应力；A为材料屈服强度；B为幂指前系数；C为应变率敏感指数；m为温度软化指数；n为加工硬化指数；εpe为等效塑性应变；＊＝pe／0，为相对等效塑性应变率，其中pe为等效塑性应变率，0为等效应变率，取0＝1.0s－1；T＊＝为无量纲温度，其中Tm，Tr分别为材料的熔点和室温温度。

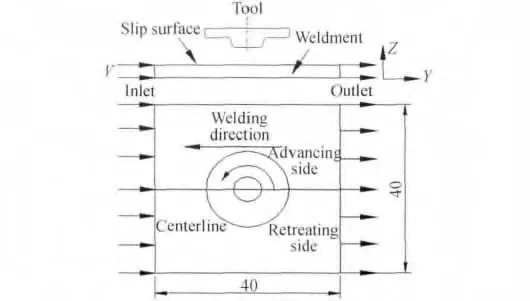
图1 6061铝合金焊件几何尺寸和边界条件Fig.1 Geometry and boundary conditions of 6061 aluminum alloy weldment

表1 6061铝合金材料参数Table1 Material parameters of 6061aluminum alloy

1.3 网格划分

采用八节点六面体线性实体减缩积分单元C3D8RT作为网格单元。该单元可以高效进行FSW过程中复杂的热力耦合问题的求解计算，并且对网格扭曲敏感性低，具有沙漏效应，抗畸变能力强。在进行网格划分时，考虑到下压过程的大变形情况和稳定焊接阶段搅拌头与焊件稳定接触的需要，将焊件划分为均匀网格。验证模型采用的6061铝合金焊接构件有限元模型如图2所示。RP为搅拌头参考点。

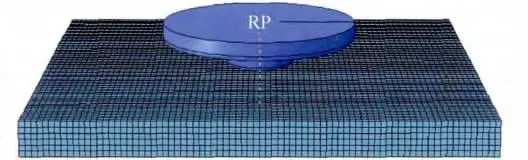
图2 6061铝合金焊件有限元模型Fig.2 Finite element model of 6061aluminum alloy weldment

1.4 ALE自适应网格处理

ALE自适应网格技术全称为“任意的拉格朗日－欧拉自适应网格”，集合了Lagrangian和Eulerian方法的优越性［3］，允许材料独立于网格运动。为解决初始焊接阶段和稳定焊接阶段由材料流动导致的网格畸变问题，应用ALE技术将这两阶段作为Lagrangian与Eulerian问题来处理。

在ABAQUS中，ALE技术的实现包含三种边界设定：Lagrangian边界、Slip边界和Eulerian边界。本工作采用Slip边界模拟搅拌头和工件表面的接触，该边界网格被强制约束与物质点同时朝表面的法线方向运动，而在切线方向可以同物质点分开，如此能够避免由搅拌头高速旋转导致的网格畸变问题，实现下压阶段搅拌头插入焊件的过程。而Eulerian边界上物质和网格可以单独运动，可以保证在下压阶段结束后顺利过渡到稳定焊接阶段。

1.5 热边界条件处理

将FSW热传导过程简化为单一热传导，即直接给焊件相应表面设置一定间隙热传系数，其中室温（20℃）下工件底面、工件表面和侧面的间隙热传系数分别为1000，100，100W／（m2·K）。

经散热后，焊件中的温度分布可通过公式（2）计算得出

式中：q为单位时间内通过间隙的热流量；θA与θB分别为间隙两面的温度值；h为间隙热传系数。

“用善骑射，杀首虏多，为汉中郎”，“用善骑射”译为“He proved himself a skillful horseman and archer”。“用”在这里是介词，表示原因，译为“因为”。英译中用“prove”这个动词来翻译，没有凸显出原文中的因果关系，只是说明李广有善骑射的才能。

另外，搅拌头与工件材料之间也发生热交换作用，且两者之间接触与间隙同时存在换热情况，在模型接触设置的热传导属性定义中，通过采用搅拌头与工件之间的接触应力来确定两者之间接触与间隙情况下的热传导系数，进而确定搅拌头与焊件之间的热交换。

由于焊接过程中存在焊缝金属的高度塑性变形，本模型考虑了金属材料的塑性变形能对温度的影响，在材料模型的热属性中通过定义塑性变形功转换为热量的系数来定义塑性变形能对温度的影响。

1.6 接触条件处理

本模型将FSW过程中搅拌针与焊件之间的接触假定为滑移摩擦类型，且由于接触面之间的相对滑动或转动量很大，往往大于接触面上的单元尺寸，将搅拌头与工件的接触关系假设为有限滑移模式。考虑到FSW过程中摩擦行为极为复杂，难以达到理想摩擦状况，本工作采用的摩擦模型为罚摩擦模型。罚摩擦允许滑移过程中发生单元特征长度很小部分的“弹性滑移”，即在黏结的接触表面间发生一个很小相对运动。在ABAQUS中设定FSW过程中罚摩擦模型的摩擦因数为0.3［2］。

1.7 模型稳定性验证

采用建立的模型模拟搅拌针转速为40rad／s、焊速为2mm／s工艺条件下，6061铝合金构件的搅拌摩擦焊接过程。设定质量放大因子200000，采用ABAQUS／Explicit模块中求解获得的动能与内能之比曲线和变形材料动能曲线来说明本模型计算结果的可靠性和稳定性［12］。当变形材料的动能与内能比值在大部分模拟时间内低于0.05时，表明所采用的质量放大因子是可以接受的。图3为数值模拟过程动能与内能之比曲线，焊接开始约0.2s后动能与内能的比值处于0.01以下，小于0.05，且保持较小值不变，模拟所取质量放大因子是可以接受的。当变形材料的动能本身或者一些代表性节点的速度变化足够平滑时，表明计算过程和计算结果是稳定的。图4为数值模拟过程焊接件的动能变化曲线。在进入稳定焊接阶段后动能曲线基本保持稳定，计算过程和计算结果是稳定的。说明本模型的计算结果在理论上是可靠、稳定的。

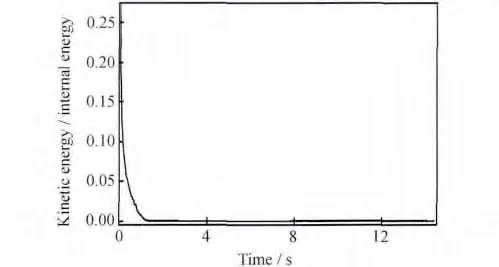
图3 6061铝合金焊件有限元模拟动能与内能之比Fig.3 The ratio of kinetic energy and internal energy of 6061aluminum alloy weldment finite element simulation

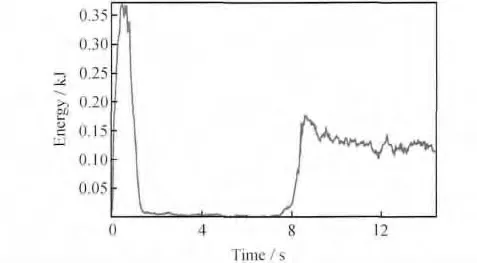
图4 6061铝合金焊件有限元模拟动能变化曲线Fig.4 The kinetic curves of 6061aluminum alloy weldment finite element simulation

2 模型分析

2.1 焊接工艺参数

搅拌针转速为40rad／s，焊速为2mm／s。整个焊接过程包括8.4s下压阶段和6s稳定焊接阶段。

2.2 温度场

图5为FSW全过程焊件纵截面温度场随时间变化图。当搅拌头刚开始插入工件时，工件的高温区主要位于搅拌头端部下方且成“V”形，搅拌头前后方的温度场成对称分布。随着搅拌头的不断插入，工件材料向外挤出，温度不断上升，并向周围扩散。当搅拌头轴肩端面与工件上表面接触后，高温区逐渐向搅拌针根部转移，直到两者完全接触。

图5 6061铝合金焊件纵截面上温度场变化（a）下压3s；（b）下压8.4sFig.5 The temperature field changes of 6061aluminum alloy weldment at the longitudinal section（a）under pressure 3s；（b）under pressure 8.4s

图6为FSW过程焊件水平方向上温度场随时间变化图。整个焊接过程最高温度在463℃左右，低于材料熔点值，未出现材料熔化的现象，符合固相连接特性。国内外研究学者一致认为在稳定焊接阶段焊缝处的最高温度基本保持不变，其数值大小主要由搅拌头的旋转速率和焊接速率所决定。而本模型所得最高温度与McClure等［13］在相同焊接工艺参数下得到的FSW过程最高温度值450℃吻合。

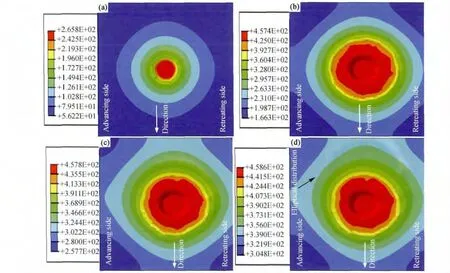
图6 6061铝合金焊件水平方向温度场变化（a）下压3s；（b）下压8.4s；（c）稳定焊接2s；（d）稳定焊接6sFig.6 The temperature field changes of 6061aluminum alloy weldment at the horizontal（a）under pressure 3s；（b）under pressure 8.4s；（c）stable welding 2s；（d）stable welding 6s

由图6（a），（b）可知，搅拌头轴肩与焊件上表面完全接触前，温度场搅拌头前后对称分布，直到进入稳定焊接阶段。轴肩与焊件上表面接触后，焊件从上到下温度场呈现高的温度梯度（图5（b），6（b））。进入稳定焊接阶段后，随着搅拌头不断迁移，温度场近似地呈椭圆形，其前方的温度梯度逐渐大于其后方的温度梯度，且最高温度值只有微小的变化，如图6（c），（d）所示。

由于在稳定焊接阶段，焊件上表面温度值主要受搅拌头旋转速率和焊接速率影响，焊件板厚与焊件下表面垫板之间的热交换对上表面影响较小。为进一步验证本模型在模拟6061铝合金FSW过程中温度场的准确性，在相同旋转速率（390r／min）和焊接速率（2.36mm／s）下，焊接稳定状态下焊件上表面横向温度分布值与Reynolds等［14］所得到的焊件上表面横向温度分布值进行比较（图7），发现模拟所得温度值与实验值吻合较好，说明建立的模型是准确有效的。

建立的模型与Hamilton等［8］建立的模型所得结果有明显不同，后者模型所得温度场的温度过高，且等效塑性应变场与实际存在较大出入，而本文所得焊接阶段的最高温度值低于材料熔点，符合FSW固相连接特性，模型真实、可靠地反映FSW全过程。

2.3 塑性变形场

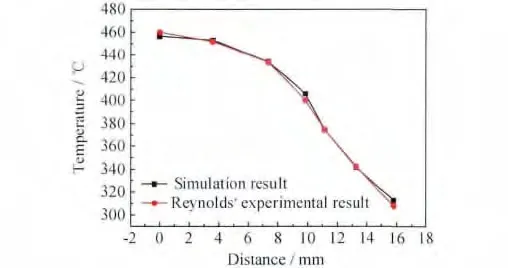
图7 6061铝合金焊件上表面温度分布值模拟结果与Reynolds实验结果对比Fig.7 Comparison of simulation and Reynolds’experimental results of temperature distribution on the upper surface of 6061aluminum alloy weldment

图8为搅拌头下压阶段不同时刻的等效塑性应变场。图8（a）为搅拌头下压5s时等效塑性应变场，此时只有搅拌针端部区域与焊件材料之间产生旋转摩擦作用，故等效塑性应变场主要位于搅拌针端部附近，且搅拌针边缘离中心最远，线速率最大，从而导致高应变区位于搅拌针边缘处。当搅拌头轴肩与焊件上表面材料接触后，焊缝区上部金属材料塑性变形场迅速增大，但限制在轴肩范围内，如图8（b）所示。

图8 6061铝合金焊件的等效塑性应变场（a）下压5s；（b）下压8.4sFig.8 The equivalent plastic strain fields of 6061aluminum alloy weldment（a）under pressure 5s；（b）under pressure 8.4s

图9为稳定焊接6s后焊件纵截面等效塑性应变场分布图。搅拌头前方等效塑性应变梯度高于搅拌头后方，且局限在一个很小范围内；搅拌头前方等效塑性应变梯度最大，远大于其后方，且等效塑性应变场主要分布于搅拌头后方。等效塑性应变值的大小直接反映了该区域材料变形的剧烈程度，在稳定焊接阶段，焊缝处的材料主要是受搅拌头的旋转和挤压作用而产生绕搅拌头旋转运动和向后方端部沉积，这必然导致在搅拌头后方端部产生较大的等效塑性应变值，与实验研究结果吻合［15］。

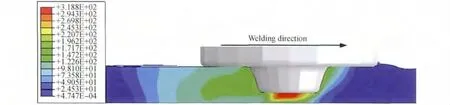
图9 6061铝合金焊件纵截面上稳定焊接6s时等效塑性应变场Fig.9 The equivalent plastic strain fields of 6061aluminum alloy weldment at the longitudinal section during stable welding 6s

图10为稳定焊接6s后焊件后方横截面处等效塑性应变场。等效塑性应变区近似成“V”形分布，高等效塑性应变区以不规则环状分布于焊缝中下部，且其中心偏向前进边侧，与XU等［16］实验所得焊核分布形态相同，前进边侧变形程度较返回边侧更剧烈，且变形范围更大，尤其是焊件上半部分。

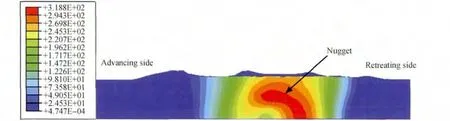
图10 6061铝合金焊件横截面上稳定焊接6s时等效塑性应变场Fig.10 The equivalent plastic strain fields of 6061aluminum alloy weldment at the cross section during stable welding 6s

图11为稳定焊接6s后焊件水平方向靠近上表面等效塑性应变场分布。可以看出，在FSW过程中，材料的等效塑性应变场在搅拌头后方呈弧形环状结构分布，等效塑性应变区偏向前进边侧。模拟所得水平方向等效塑性应变场前进边侧等效塑性应变值明显大于返回边侧，与实验结果“前进边的标示材料层破坏的程度明显大于返回边的现象说明，在前进边所发生的材料变形剧烈程度更大”［15］相吻合。

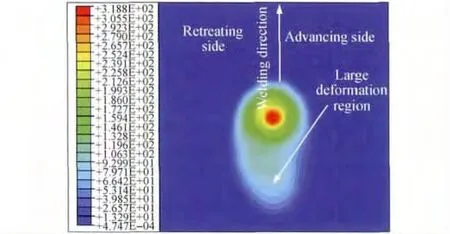
图11 6061铝合金焊件靠近上表面稳定焊接6s时水平方向等效塑性应变场Fig.11 Equivalent plastic strain fields of 6061aluminum alloy weldment at the horizontal near upper surface during stable welding 6s

3 结论

（1）基于ALE网格自适应技术解决了搅拌摩擦焊接过程中出现的网格高度畸变问题。

（2）实现了搅拌摩擦焊接全过程的温度场和塑性变形场的仿真分析，且所得焊缝处等效塑形应变场分布与实验所得焊缝处组织结构具有良好对应性。

（3）模拟所得6061铝合金FSW过程最高温度值与实验最高温度值之间的误差为2.89%，且焊件上表面在横向温度的分布与实验数值有良好的吻合。

［1］THOMAS W M，NICHOLAS E D，NEEDHAM J C，et al.Friction Stir Welding［P］.UK Patent：9125978.8，1991－12－06.

［2］SCHMIDT H，HATTEL J.A local model for the thermo mechanical conditions in friction stir welding［J］.Modelling and Sim－ulation in Materials Science and Engineering，2005，13（1）：77－93.

［3］XU S，DENG X.A three dimensional model for the friction stir welding process［A］.CD－ROM Proceedings of the 21st Southeastern Conference on Theoretical and Applied Mechanics（SECTAM XXI）［C］.Orlando，Florida：University of Central Florida，2002.699－704.

［4］张昭，别俊.搅拌摩擦焊接过程数值仿真的完全热力耦合模型［J］.中国机械工程，2008，19（10）：1240－1245.ZHANG Z，BIE J.Fully coupled thermo－mechanical model for numerical simulation of friction stir welding process［J］.Chinese Journal of Mechanical Engineering，2008，19（10）：1240－1245.

［5］鄢东洋，史清宇，吴爱萍，等.搅拌摩擦焊接的热力耦合分析模型［J］.机械工程学报，2010，46（16）：106－112.YAN D Y，SHI Q Y，WU A P，et al.Developmental thermalmechanical coupled analysis model for friction stir welding［J］.Journal of Mechanical Engineering，2010，46（16）：106－112.

［6］GUO Z H，ZHAO G Y，KE L M，et al.Thermo－mechanical coupled analysis of deformation behavior in friction stir welding process of aluminum 7075plate with conical pin［J］.Advanced Materials Research，2011，338：618－621.

［7］MANDAL S，RICE J，ELMUSTAFA A A.Experimental and numerical investigation of the plunge stage in friction stir welding［J］.Journal of Materials Processing Technology，2008，203（1－3）：411－419.

［8］HAMILTON R，MACKENZIE D，LI H J.Multi－physics simulation of friction stir welding process［J］.Engineering Computations，2010，27（8）：967－985.

［9］YU M，LI W Y，LI J L，et al.Modeling of entire friction stir welding process by explicit finite element method［J］.Materials Science and Technology，2012，28（7）：812－817.

［10］JOHNSON G R，COOK W H.Fracture characteristics of three metals subjected to various strains，strains rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21（1）：31－48.

［11］ZHANG Z，CHEN J T.Computational investigations on reliable finite element－based thermo－mechanical coupled simulations of friction stir welding［J］.Adv Manuf Technol，2011，60（9－12）：959－975.

［12］张昭，张洪武.接触模型对搅拌摩擦焊接数值模拟的影响［J］.金属学报，2008，44（1）：85－90.ZHANG Z，ZHANG H W.Effect of contact model on numerical simulation of friction stir welding［J］.Acta Metallurgica Sinica，2008，44（1）：85－90.

［13］McCLURE J C，FENG Z，TANG W，et al.A thermal model of friction stir welding［A］.Proc 5th Int Conf on Trends in Welding Research［C］.Pine Mountain：ASM International，1998.590－595.

［14］KHANDKAR M Z H，KHAN J A，REYNOLDS A P.A thermal model of the friction stir welding process［A］.ASME International Mechanical Engineering Congress ＆ Exposition［C］.New Orleans，Louisiana：ASME，2002.115－124.

［15］柯黎明.搅拌摩擦焊接头成形规律研究［D］.北京：清华大学，2007.KE L M.An investigation on the formation mechanism of the friction stir welds［D］.Beijing：Tsinghua University，2007.

［16］XU S，DENG X.A study of texture patterns in friction stir welds［J］.Acta Materialia，2008，56（6）：1326－1341.